قضیه اصلی حساب — به زبان ساده

یکی از قضیههای مهم و اساسی در نظریه اعداد، قضیه اصلی حساب (Fundamental Theorem of Arithmetic) است که گاهی به آن «قضیه تجزیه یکتا» (Unique Factorization Theorem) یا «قضیه تجزیه به عوامل اول یکتا» (Unique-Prime-Factorization Theorem) نیز میگویند. از کاربردهای آن میتوان به تجزیه اعداد مرکب و پیدا کردن اعداد اول و همچنین محاسبه بزرگترین مقسوم علیه مشترک (ب-م-م) و کوچکترین مضرب مشترک (ک-م-م) اشاره کرد.
از آنجایی که مجموعه اعداد طبیعی و صحیح و تقسیم آنها، موضوع مورد بحث در این قضیه هستند، توصیه میشود که مطلب قواعد بخش پذیری یا عاد کردن --- به زبان ساده را قبل از مطالعه این نوشتار بخوانید. از طرفی خواندن نوشتارهای اعداد طبیعی — به زبان ساده و اعداد صحیح — به زبان ساده به همراه تقسیم عدد صحیح — به زبان ساده به عنوان مقدمه ضروری است. همچنین مطالعه الگوریتم تقسیم اعداد — از صفر تا صد و ب م م یا بزرگترین مقسوم علیه مشترک چیست؟ — به زبان ساده خالی از لطف نیست و به استحکام بحث کمک میکند.
قضیه اصلی حساب
قضیه اساسی حساب، راه را برای تعیین «اعداد مرکب» (Composite Number) و «عدد اول» (Prime Number) باز کرده است. طبق این قضیه، هر عدد صحیح (مخالف ۱) یا یک عدد اول است یا یک عدد مرکب که میتواند به شکل منحصر به فردی توسط ضرب اعداد اول بیان شود.
برای مثال عدد ۱۲۰۰ را میتوان به صورت عاملها یا اعداد اول ۲ و ۳ و ۵ به شکل زیر نوشت:
این قضیه دو موضوع را مورد بررسی قرار میدهد. اول از همه تعیین میکند که هر عدد مرکب را میتوان به صورت حاصلضرب اعداد اول نوشت و در گام بعدی مشخص میشود که این حاصلضرب برحسب عوامل، یکتا و منحصر به فرد است.
برای مثال مشخص است که ۱۲۰۰ را میتوان فقط براساس عوامل اول ۲ و ۳ و ۵ و توانهای مختلف آنها نوشت. هر چند ممکن است ترتیب ضربها متفاوت باشد ولی عوامل و توانهای آنها همیشه یکسان هستند.
نکته: عوامل یا فاکتورها، در قضیه اصلی حساب باید اعداد اول باشند، در غیر اینصورت دیگر عاملها منحصر به فرد نخواهند بود. برای مثال عدد ۱۲ را میتوانستیم به صورتهای مختلفی از عوامل تجزیه کنیم که لزوما اول هم نباشند.
یکی از دلایلی که عدد ۱ را عضوی از مجموعه اعداد اول فرض نمیکنند، وجود این قضیه است. در صورتی که عدد ۱ نیز به عنوان عدد اول در نظر گرفته میشد، آنگاه تجزیه به عوامل اول، منحصر به فرد محسوب نمیشد.
قبل از هر چیز اصطلاحی را معرفی میکنیم که بسیار مرتبط به اعداد صحیح و مبحث تقسیم و تجزیه به عوامل اول است.
بخشپذیری یا عاد کردن
فرض کنید و دو عدد صحیح باشند، آنگاه اگر تقسیم بر نیز یک عدد صحیح بوده و باقیمانده برابر با صفر باشد، عبارتهای زیر را معادل در نظر میگیرند.
- ، عدد را عاد میکند.
- ، بر بخشپذیر است.
- ، مضربی از است.
- ، مقسوم علیه است.
- ، عدد را میشمارد.
این عبارتها را به بیان و نماد ریاضی به صورت زیر نشان میدهیم:
و میخوانیم عدد را عاد میکند. قوانین و قضیههای مربوط به بخشپذیری و عاد کردن را در قواعد بخش پذیری یا عاد کردن --- به زبان ساده مطالعه کنید.

تاریخچه قضیه اصلی حساب
اولین بار این قضیه (حداقل به عنوان یک قضیه) توسط اقلیدس در کتاب اصول هندسه، جلد هفتم گزاره ۳۰ تا ۳۲ و همچنین جلد نهم در گزاره ۱۴، حدود ۳۰۰ سال قبل از میلاد معرفی شد. او در گزاره ۳۰ چنین گفته است:
«اگر دو عدد در یکدیگر ضرب شوند و عدد جدیدی بسازند و حاصلضرب بر یک عدد اول، تقسیمپذیر باشد، آن عدد اول یکی از اعداد اصلی مربوط به حاصلضرب را هم میشمارد.»
این موضوع را به زبان امروزی میتوان به این صورت بیان کرد که اگر عدد اول حاصلضرب را بشمارد، آنگاه حتما یکی از اعداد یا را عاد خواهد کرد. البته مشخص است که این گزاره فقط در صورتی صحیح است که عددی که تقسیم بر آن صورت میگیرد، یک عدد اول باشد، در غیر این صورت، گزاره اشتباه خواهد بود.
این قضیه که کلید اصلی برای اثبات قضیه اصلی حساب است، گاهی «لم اقلیدس» (Euclid's Lemma) نیز نامیده میشود.
همچنین گزاره ۳۱ که توسط اقلیدس در اصول هندسه، بیان شده به شکل زیر است: «هر عدد مرکب توسط یک یا چند عدد اول، شمارش (عاد) میشود.»
این گزاره را میتوان به این شکل بیان کرد که هر عدد صحیح بزرگتر از ۱، حتما یک مقسوم علیه اول دارد.
ا زطرفی، گزاره شماره ۳۲ نیز در مورد طبقهبندی اعداد صحیح نوشته شده است: «هر عدد، یا اول است یا توسط یک عدد اول شمرده میشود.»
این گزاره خبر بسیار خوبی به ما میدهد و مشخص میکند که تجزیه به عاملهای اول میسر است. به این ترتیب پایههای قضیه اصلی حساب ریخته میشود.
در انتها نیز گزاره ۱۴ از جلد نهم را میآوریم: «اگر یک عدد، کوچکترین عددی باشد که توسط حاصلضرب اعداد اول ساخته شده، آنگاه توسط هیچ عدد اول دیگری شمرده نخواهد شد.»
به بیان ریاضیات مدرن میتوان این گزاره به این صورت در نظر گرفت که کوچکترین مضرب مشترک چندین عدد اول، مضربی از اعداد اول دیگر نیست. این موضوع ابتدای راه اثبات یکتا بودن تجزیه اعداد مرکب به عوامل اول است.
بعدها، «کارل گاوس» (Johann Carl Friedrich Gauss) در کتاب «پرسشهای ریاضی» (Disquisitiones Arithmetica) اثبات قضیه اصلی حساب را ارائه کرد و «حساب پیمانهای» (Modular Arithmetic) که پایه محاسبات رایانههای امروزی است را بنا نهاد.

قضیه اصلی حساب و اثبات آن
شکل رسمی قضیه اصلی حساب به صورت زیر نوشته میشود.
قضیه اصلی حساب: هر عدد صحیح را میتوان به صورت منحصر به فردی از حاصلضرب عوامل یا اعداد اول نوشت، به شرطی که .
نکته: منظور از منحصر به فرد ترتیب ضرب نیست بلکه اعداد اول و توانهای آنها است.
برهان شامل دو قسمت میشود، در بخش اول امکان تجزیه و در قسمت دوم منحصر به فرد بودن تجزیه اثبات میشود. برای سادگی، اثبات را برای اعداد طبیعی انجام میدهیم. بدیهی است که به راحتی میتوان این روش را برای اعداد صحیح نیز به کار گرفت. در اینجا به روش استقرا، قضیه را ثابت میکنیم.
اثبات:
- فرض کنید ، از آنجایی که ۲ عدد اول است، پس حکم برقرار است.
- فرض کنید که قضیه برای هر عدد طبیعی برقرار باشد.
- برای عدد طبیعی ، دو وضعیت در نظر میگیریم، اگر اول باشد که خودش برحسب عامل بوده و احتیاج به تجزیه ندارد. ولی اگر مرکب باشد، اعداد طبیعی دیگری مانند و وجود دارند که:
پس هم و هم طبق فرض استقرا، قابل تجزیه به عوامل اول هستند، زیرا از کوچکتر بوده و حکم استقرا برایشان صادق است. پس میتوان نوشت:
که در آنها و اعداد اول بوده و لزوما متفاوت نیز نیستند. پس داریم:
در نتیجه عدد نیز به صورت حاصلضرب اعداد اول نوشته شد.
در گام دوم باید نشان دهیم که این عوامل، یکتا هستند. اثبات این قسمت نیز توسط استقرا صورت میگیرد. فرض کنید عدد طبیعی دارای دو شیوه تجزیه به عوامل اول باشد، بطوری که:
نشان میدهیم که و عوامل و بطور متناظر، یکی هستند. استقرا را روی انجام میدهیم.
- فرض کنید در نتیجه حکم برقرار است. زیرا عدد اول است.
- فرض کنید قضیه برای برقرار بوده، باید نشان دهیم که برای نیز برقرار است.
- از آنجایی که ، پس ، عدد را میشمارد و داریم پس در نتیجه حداقل یکی از ها توسط شمرده میشوند که خلاف اول بودن آنها است مگر آنکه با هم برابر باشند. در نتیجه هستند.
- بر این اساس، با تغییر اندیس و استفاده از فرض استقرا، نتیجه میگیریم که تجزیه به عوامل اول یکتا است.
به این ترتیب اثبات تجزیه به همراه یکتایی قضیه اصلی حساب صورت میپذیرد.
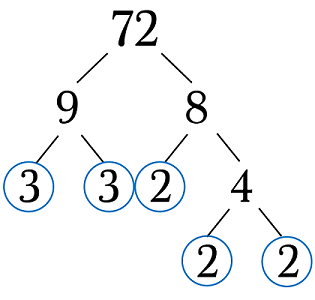
فرم استاندارد یا تجزیه کانونی اعداد مرکب
هر عدد صحیح بزرگتر از ۱ (اعداد طبیعی) را میتوان به صورت حاصلضرب اعداد اول و توانهای صحیح نوشت. بنابراین اگر را یک عدد طبیعی یا مرکب با شرایط گفته شده در نظر بگیریم و تا نیز، عدد اول باشند که ، آنگاه طبق قضیه اصلی حساب، تجزیه کانونی (Canonical Representation) یا فرم استاندارد (Standard Form) یک عدد مرکب (یا حتی اول) را میتوان به صورت زیر نمایش داد.
به عنوان مثال
نکته: اگر در نظر گرفته شود، آنگاه میتوان هر عدد طبیعی را به صورت حاصلضرب همه اعداد اول (حاصلضرب نامتناهی) نوشت:
عملگرهای ریاضی
به کمک نمایش کانونی یا فرم استاندارد اعداد طبیعی (صحیح) میتوان بزرگترین مقسوم علیه مشترک (ب-م-م) که آن را با نشان داده یا کوچکترین مضرب مشترک (ک-م-م) یا دو عدد را به راحتی پیدا کرد.
دو عدد و را در نظر بگیرید. بطوری که
آنگاه
به این ترتیب، برای مثال بزرگترین مقسوم علیه مشترک بین ۱۲ و ۱۵، برابر با ۳ است، زیرا:
و
پس
همچنین کوچکترین مضرب مشترک دو عدد ۱۲ و ۱۵ نیز برابر با خواهد بود.

خلاصه و جمعبندی
در این نوشتار با قضیه اصلی حساب (Fundamental Theorem of Arithmetic) و تجزیه اعداد به عوامل اول، آشنا شدیم. به این ترتیب توانستیم اعداد مرکب را به شکلی منحصر به فرد و یکتا به صورت حاصلضرب اعداد اول بنویسیم. روشهای تشخیص عدد مرکب و عدد اول نیز در این نوشتار مرور و مورد بررسی قرار گرفت.
همچنین تاریخچه قضیه اصلی حساب و روش اثبات آن نیز مرور و معرفی شد. این قضیه، نقش اساسی در نظریه اعداد (Number Theory) ایفا میکند و بخصوص در محاسبات تقسیم اعداد در رایانهها به کار گرفته میشود.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش ریاضی پایه دانشگاهی
- مجموعه آموزشهای دروس رسمی دبیرستان و پیشدانشگاهی
- تقسیم عدد صحیح — به زبان ساده
- اعداد طبیعی — به زبان ساده
- اعداد گویا — به زبان ساده
- الگوریتم تقسیم اعداد — از صفر تا صد
^^












