قضیه استوکس — به زبان ساده

پیشتر در بلاگ فرادرس قضیه گرین را توضیح دادیم. همانطور که عنوان شد میتوان با استفاده از قضیه مذکور، انتگرالِ خطیِ یک میدان برداری را بر حسب انتگرال دوگانه روی سطح محصور در آن بیان کرد. در این مطلب قصد داریم تا ورژن قضیه گرین را در حالت سهبعدی بیان کنیم. در حقیقت «قضیه استوکس» (Stokes' Theorem) موضوعی است که قصد داریم آن را توضیح دهیم.
صورت قضیه استوکس
جهت تشریح قضیه، در ابتدا مطابق با شکل زیر خم C را در نظر بگیرید. فرض کنید این خم، در واقع مرزِ سطحی سهبعدی است.
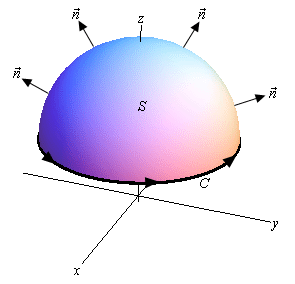
توجه داشته باشید که اگر جهت C پادساعتگرد باشد، جهت بردارهای عمود به صفحه (n) نیز به سمت بیرون و در صورت ساعتگرد بودن منحنی C، جهت بردارهای n به سمت داخل در نظر گرفته میشوند (شکل فوق). در حقیقت جهت C و جهت بردار n بایستی هماهنگ با هم در نظر گرفته شوند. با این فرضیات قضیه استوکس را میتوان مطابق با رابطه زیر توصیف کرد.
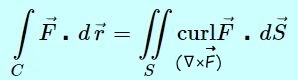
در رابطه فوق S سطحی با مرز C است. نکته جالب در قضیه فوق این است که رابطه بالا برای هر سطحی با مرز C صادق است. با استفاده از این قضیه انتگرالهای روی یک خم را بهراحتی میتوان بدست آورد. جهت درک بهتر قضیه پیشنهاد میکنیم به مثالهای زیر توجه فرمایید.
مثال ۱
با استفاده از قضیه استوکس، حاصل انتگرال را روی سطح z بدست آورید. تابع برداری F را بهصورت زیر در نظر بگیرید.
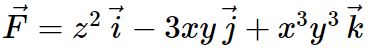
از طرفی سطح z را بالای صفحه z=1 و برابر با z=5-x2-y2 فرض کنید.
پاسخ: جهت استفاده از قضیه استوکس در ابتدا بایستی سطح S مشخص شود. با توجه به فرض مسئله، سطح توصیف شده بهشکل زیر خواهد بود. از طرفی تابع F، برداری چند متغیره است.
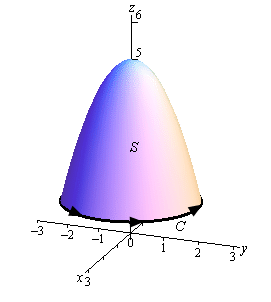
بایستی بدانید که محل برخورد توابع z=5-x2-y2 و z=1، خم C را تولید میکند. در نتیجه معادله نشان دهنده خم C، بهصورت زیر بدست خواهد آمد.
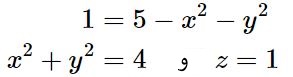
رابطه بالا خمی بهشکل دایره را نشان میدهد که در فاصله z=1 از مبدا مختصات قرار گرفته است. توجه داشته داشید که انتگرال بیان شده بهصورت برداری است؛ در نتیجه بایستی منحنی C بهصورت برداری بیان شود. بنابراین اگر x برابر با 2cos t و y برابر با 2sin t در نظر گرفته شوند، حاصل جمع توان دوم آنها برابر با ۴ خواهد بود. از این رو توابع انتخاب شده برای x و y، در رابطه مربوط به خم C (رابطه فوق) صادق هستند. در حقیقت تابع برداری زیر خم C را نشان میدهد.
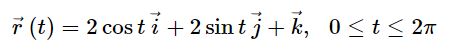
توجه داشته باشید که دو مولفهی اول رابطه فوق، دایره و مولفه سوم () فاصله آن را از مبدا نشان میدهد. در مرحله بعد بایستی دیفرانسیل را بیان کنیم. اگر باشد، دیفرانسیل بدست میآید. حال با اعمال قضیه استوکس داریم:
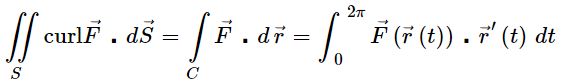
انتگرال بالا بر حسب متغیر t بیان شده؛ بنابراین تابع F نیز بایستی بر حسب t جایگذاری شود. بهمنظور انجام این کار، متغیرهای x,y,z را که بر حسب t ارائه شده در تابع F قرار میدهیم.
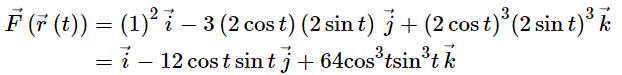
با توجه به تابع F بدست آمده، زمان آن رسیده تا توابع تحت انتگرال را بهصورت زیر بدست آوریم.
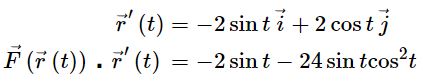
نهایتا حاصل انتگرال بهصورت زیر بدست میآید.
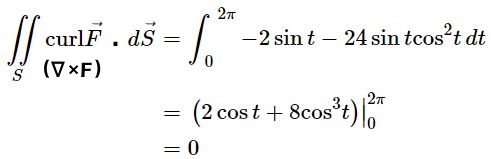
مثال ۲
با استفاده از قضیه استوکس حاصل انتگرال را بدست آورید.
تابع F را نیز مطابق با رابطه زیر در نظر بگیرید.
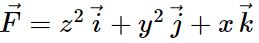
همچنین C مثلثی با رئوس (1,0,0) ، (0,1,0) و (0,0,1) است که جهت خم آن نیز بهصورت پادساعتگرد در نظر گرفته شده است. در شکل زیر، تصویر مثلث مذکور نشان داده شده است.
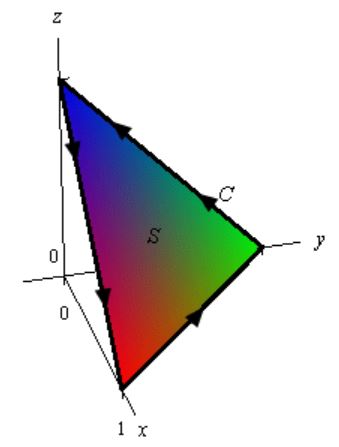
با توجه به پادساعتگرد بودن خم، جهت بردار به سمت بیرون از صفحه در نظر گرفته میشود. معادله صفحه برابر است با:
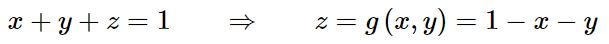
حال با استفاده از قضیه استوکس، انتگرال سطحی تابع F روی خم C برابر با تابع زیر بدست میآید. از این رو در اولین قدم بایستی کرل تابع برداری F تعریف شود. کرل F برابر است با:
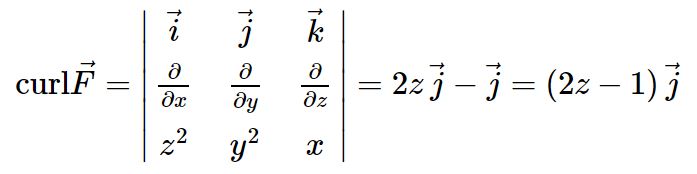
با توجه به تابع بدست آمده، حاصل انتگرال روی سطح به شکل زیر نوشته میشود.
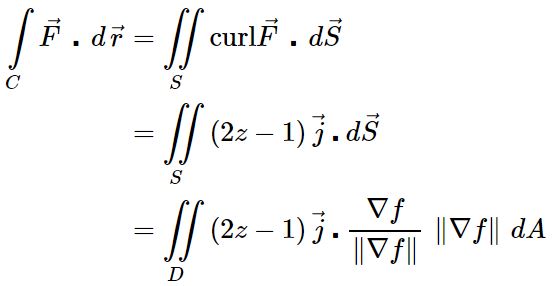
توجه داشته باشید که در عبارت بالا، نشان دهنده بردار واحد عمود به صفحه است. جهت محاسبه انتگرال فوق به دو مقدار نیازمندیم. در ابتدا بایستی گرادیان f را بهشکل زیر بیابیم.
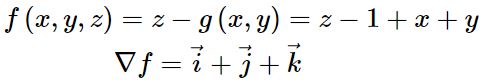
رابطه بالا نشان میدهد جهت بدست آمده به سمت بیرون از صفحه است که مطابق با فرض ما است. بنابراین جهت بدست آمده صحیح است. توجه داشته باشید که با توجه به رابطه ۱ انتگرال روی سطح S به انتگرال روی D تبدیل شده است. از طرفی سطح D، تصویر شده سطح S روی صفحه x-y است. در زیر سطح D نشان داده شده است.
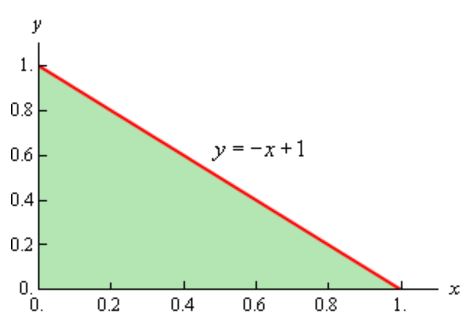
اگر مقدار z=0 را در معادله صفحهی S قرار دهیم، خواهیم دانست که مقدار x در بازه ۰ تا ۱ قرار دارد. همچنین متغیر y بین ۰ تا x+1- تغییر میکند. در حقیقت دو بازهی زیر توصیف کننده سطح D هستند.
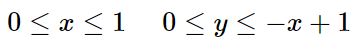
با توجه به بازههای تعریف شده برای x و y، رابطه ۱ را میتوان بهشکل زیر بازنویسی کرد.
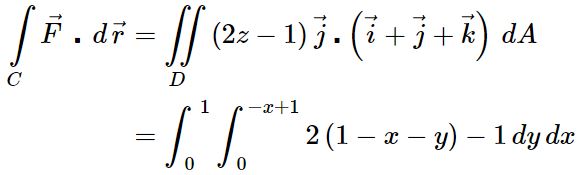
توجه داشته باشید جهت محاسبه انتگرال دوگانه فوق، متغیر z بایستی برابر با صفر قرار داده شود. نهایتا حاصل انتگرال تابع برداری F روی خم C برابر است با:
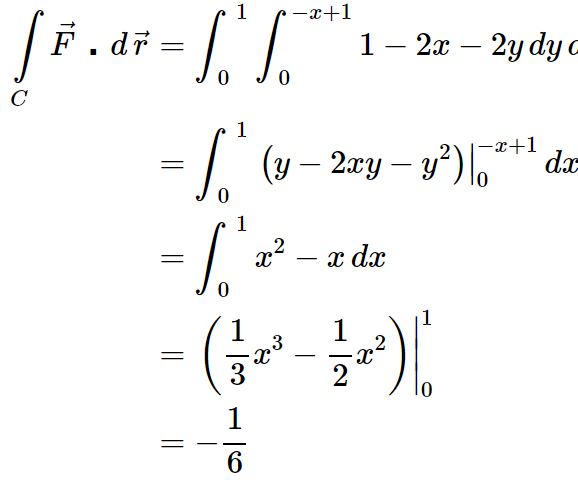
در هر دو مثال ۱ و ۲ با انتگرالهایی روبهرو بودیم که در آنها عبارت تحت انتگرال پیچیده به نظر میرسید؛ اما با استفاده از قضیه استوکس، محاسبه انتگرال آسانتر شده است. البته در آینده انتگرال خطی یک میدان اسکالر را نیز توضیح خواهیم داد.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضیات، آموزشهای زیر نیز به شما پیشنهاد میشوند:













سلام، توضیحاتی که کلا تو مباحثی که ارایه کردید واقعاً عالیه و دید خیلی خوبی به خواننده راجع به مطلب میده، فقط در مورد قضیه استوکس کاش دلیل رابطه و اثباتش رو هم توضیح بدید که چرا کار روی مرز برابر کرل میدان روی سطح هست. با تشکر.