قانون بیوساوار (Biot Savart law) — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در مقاله «میدان مغناطیسی جریان — از صفر تا صد» با قانون بیوساوار (Biot Savart law) آشنا شدیم. دیدیم که قانون مذکور در واقع معادلهای در فیزیک الکترومغناطیس است که میدان مغناطیسی حاصل از جریان را محاسبه میکند. قانون بیوساوار به فرم زیر است:
(1)
همانطور که در معادله فوق مشخص است، میدان مغناطیسی حاصل از جریان به مقدار و جهت جریان و فاصله از سیم حامل جریان بستگی دارد. نیز ضریب گذردهی (تراوایی) مغناطیسی خلأ با مقدار است. در ادامه این مقاله با ما همراه باشید تا با زبانی ساده با روند ریاضی استخراج معادله قانون بیوساوار از معادلات ماکسول آشنا شوید.
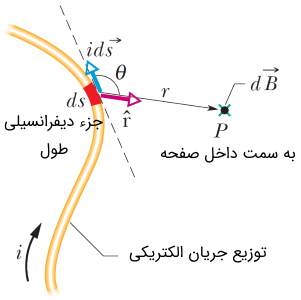
قانون بیوساوار
در ادامه نحوه به دست آوردن معادله قانون بیوساوار (رابطه ۱) را در چند مرحله بیان میکنیم.
قانون بیوساوار در حدود سال 1820 توسط بیون (Jean-Baptiste Biot) و ساوار (Félix Savart) جهت محاسبه میدان مغناطیسی ناشی از جریان الکتریکی که درون یک سیم جاری است، ارائه شد.

تعریف پتانسیل برداری
در مقاله «فرم دیفرانسیلی معادلات ماکسول -- به زبان ساده» دیدیم که فرم دیفرانسیلی قانون گاوس در مغناطیس به شکل زیر است.
(2)
رابطه فوق بیان میکند که تک قطبی مغناطیسی نمیتواند وجود داشته باشد. در مباحث هندسه تحلیلی یا ریاضیات کاربردی دیدیم که که برای هر میدان برداری دلخواه رابطه زیر برقرار است.
(3)
رابطه فوق بیان میکند که دیورژانسِ کرل یک میدان برداری برابر با صفر است. با توجه به رابطه فوق، میتوانیم میدان مغناطیسی را به صورت کرل یک میدان برداری به شکل زیر بنویسیم.
(4)
در فیزیک الکترومغناطیس، پارامتر به پتانسیل برداری موسوم است.
نوشتن قانون آمپر برحسب پتانسیل برداری
در مقاله «قانون آمپر -- به زبان ساده» دیدیم که معادله ریاضی بیانگر قانون مذکور به فرم زیر است.
(5)
حال با استفاده از قضیه استوکس (Stokes' theorem) میتوانیم رابطه فوق را به صورت دیفرانسیلی زیر بنویسیم.
(6)
(7)
با نوشتن میدان مغناطیسی برحسب پتانسیل برداری (رابطه ۴) داریم:
(8)
از مباحث روشهای ریاضی در فیزیک میدانیم که حاصل جمله سمت چپ رابطه فوق به صورت زیر در میآید:
(9)

از آنجایی که پتانسیل برداری تعریف شده منحصر به فرد نیست، میتوانیم به طور دلخواه دیورژانس آن را بدون آنکه تاثیری بر میدان مغناطیسی داشته باشد، صفر در نظر بگیریم. این امر به پیمانه کولن (Coulomb Gauge) موسوم است. در واقع ما پتانسیلی را انتخاب میکنیم که برایمان مناسبتر باشد و راه حل ریاضی را کوتاه کند. پس داریم:
(10)
با توجه به عبارت فوق، معادله (8) به فرم زیر در میآید:
(11)
رابطه فوق به معادله پواسون برای پتانسیل برداری معروف است.
حل معادله پواسون
حل معادله پواسون () بسیار شبیه به راه حل معادله پواسون در الکترواستاتیک () است. معادله پواسون در الکترواستاتیک که پتانسیل ناشی از توزیع بار را نتیجه میدهد، راه حلی جهت کاهش محاسبات از طریق قانون کولن است. جهت آشنایی با حل معادله پواسون در فیزیک الکتریسیته و مغناطیس به دو مقاله «پتانسیل مغناطیسی — به زبان ساده» و «حل مسائل الکتریسیته ساکن — به زبان ساده» مراجعه فرمایید.
در اینجا نیز قصد داریم تا از حل این معادله پواسون برای پتانسیل برداری مغناطیسی به قانون بیوساوار برسیم که توصیف کننده میدان مغناطیسی ناشی از جریان بار الکتریکی است.
با حل معادله (11)، به پاسخ زیر برای پتانسیل برداری میرسیم.
(12)
محاسبه کرل پتانسیل برداری
پیشتر بیان کردیم که میدان مغناطیسی برابر با کرل پتانسیل برداری است. پس میتوانیم با گرفتن کرل از رابطه (12) به میدان مغناطیسی برسیم. در نتیجه داریم:
(13)
با استفاده از رابطه ریاضی زیر:
(14)
نتیجه میشود:
(15)
دقت داشته باشید که عملگر در اینجا روی متغیر اثر میکند. از آنجایی که برحسب است، حاصل صفر میشود. در نتیجه داریم:
(16)
(17)
در بالا از رابطه ریاضی استفاده کردیم. میدانیم که تعریف چگالی جریان الکتریکی به صورت زیر است:
(18)
در نتیجه میتوانیم عبارت را به صورت بنویسیم. با جایگذاری مقدار مذکور در رابطه (17) و همچنین تعریف ، قانون بیوساوار به فرم زیر نتیجه میشود.
(19)
همانطور که پیشتر بیان کردیم، کاربرد معادله قانون بیوساوار در محاسبه میدان مغناطیسی ناشی از جریان الکتریکی در اطراف ساختاری است که بتوان آن را به صورت جزهای دیفرانسیلی طولی درنظر گرفت.
اگر برایتان سوال است که که چرا مخرج رابطه فوق دارای توان ۳ بوده، درحالی که قانون بیوساوار معرفی شده در رابطه (۱) در ابتدای مقاله دارای توان ۲ است؛ با استفاده از تعریف بردار یکه میتوانید به راحتی رابطه (۱) را به فرم رابطه (19) تبدیل کنید.
(20)
در ادامه در نظر داریم تا بررسی دو مثال و استفاده از قانون بیوساوار بپردازیم.
مثال
سیم نامحدودی را در نظر بگیرید که جریان الکتریکی از آن میگذرد. مطابق با شکل (7) در نظر داریم تا با استفاده از قانون بیوساوار به محاسبه میدان مغناطیسی ناشی از جریان الکتریکی از جزء دیفرانسیلی طول بپردازیم.
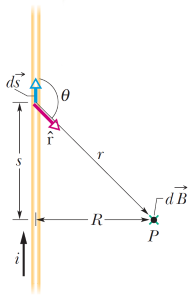
با توجه به حاصل ضرب یا قانون دست راست، جهت بردار میدان مغناطیسی به سمت داخل صفحه است. با نوشتن قانون بیوساوار برای ساختار شکل فوق، روند محاسبه میدان مغناطیسی را شروع میکنیم.
(21)
(22)
با توجه به شکل (7)، متغیر و به جزء دیفرانسلی طول وابستهاند. در نتیجه باید معادل آنها در رابطه انتگرالی (22) جایگذاری کنیم. در نتیجه:
(23)
(24)
با توجه به دو رابطه فوق، معادله (22) به فرم زیر در میآید:
(25)
با توجه به رابطه فوق، میدان مغناطیسی ناشی از حرکت بار الکتریکی (جریان) در اطراف یک سیم حامل حریان بینهایت برابر با مقدار است. اگر سیم را شبه نامحدود فرض کنیم، به دلیل تغییر در حدود انتگرال، میدان به مقدار کاهش پیدا میکند.
همانطور که در فوق مشاهده کردید، محاسبه میدان مغناطیسی به وسیله قانون بیوساوار نیازمند حل انتگرالهای زمانبر است. یک راه حل ساده و کوتاهتر جهت محاسبه میدان مغناطیسی، استفاده از قانون آمپر است. جهت آشنایی با قانون آمپر و مدل تعمیم یافته آن، به مقاله «قانون آمپر -- به زبان ساده» مراجعه فرمایید.
مثال
در اینجا قصد داریم تا با استفاده از قانون بیوساوار به محاسبه میدان مغناطیسی ناشی از سیمی خم شده حامل جریان الکتریکی که قطاعی از دایره را تشکیل میدهد (شکل ۸)، بپردازیم.
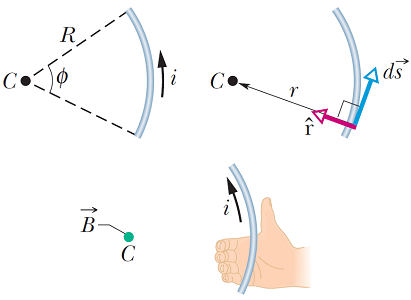
با توجه به شکل فوق و زاویه بین دو بردار و یکه داریم ( در اینجا است):
(26)
(27)
با توجه به شکل میتوانیم تعریف کنیم:
(28)
(29)
با توجه به رابطه فوق، میدان در مرکز یک سیم دایره کامل () حامل جریان برابر با میشود.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- امواج مایکروویو (Microwave) یا ریز موج -- به زبان ساده
- امواج رادیویی -- به زبان ساده
- مخابرات فیبر نوری -- به زبان ساده
- دوقطبی الکتریکی (Electric Dipole) — به زبان ساده
^^













سلام بنده رسولی هستم دانشجوی ارشد میکروالکترونیک دانشگاه ارومیه .
از قانون بیو ساوار برای پیداکردن میدان مغناطیسی حول یک صفحه حامل جریان استفاده میکنم .نتیجه اش میشه یه انتگرال دوگانه که نمیدونم درست حلش کردم یا نه ممنون میشم اگر کمکم کنید اگرم امکانش باشه میخواستم با خود اقای ابوالحسنی در این مورد صحبت کنم متاسفانه هیچ لینکی از ایشون ندارم.