فرمول های مشتق مهم + سوال با جواب و دانلود PDF
مشتق، یکی از مفاهیم مهم و پرکاربرد در دنیای ریاضیات است. این مفهوم، در سطوح متوسطه و به همراه مفاهیم دیگری نظیر حد و پیوستگی آموزش داده میشود. مشتق توابع مختلف، فرمولهای مخصوص به خود را دارند. درک مبانی به دست آوردن این فرمولها و به خاطر سپردن مهمترین آنها، شما را به حل بسیاری از مسائل مرتبط در این حوزه کمک میکند. در این مقاله، به معرفی مهمترین فرمول های مشتق به همراه حل چندین مثال و تمرین میپردازیم. علاوه بر این، فایل PDF پرکاربرترین فرمولها و قوانین مشتقگیری را ارائه میکنیم. با مطالعه این فایل میتوانید فرمول های مهم مشتق گیری را به سرعت مرور کنید.

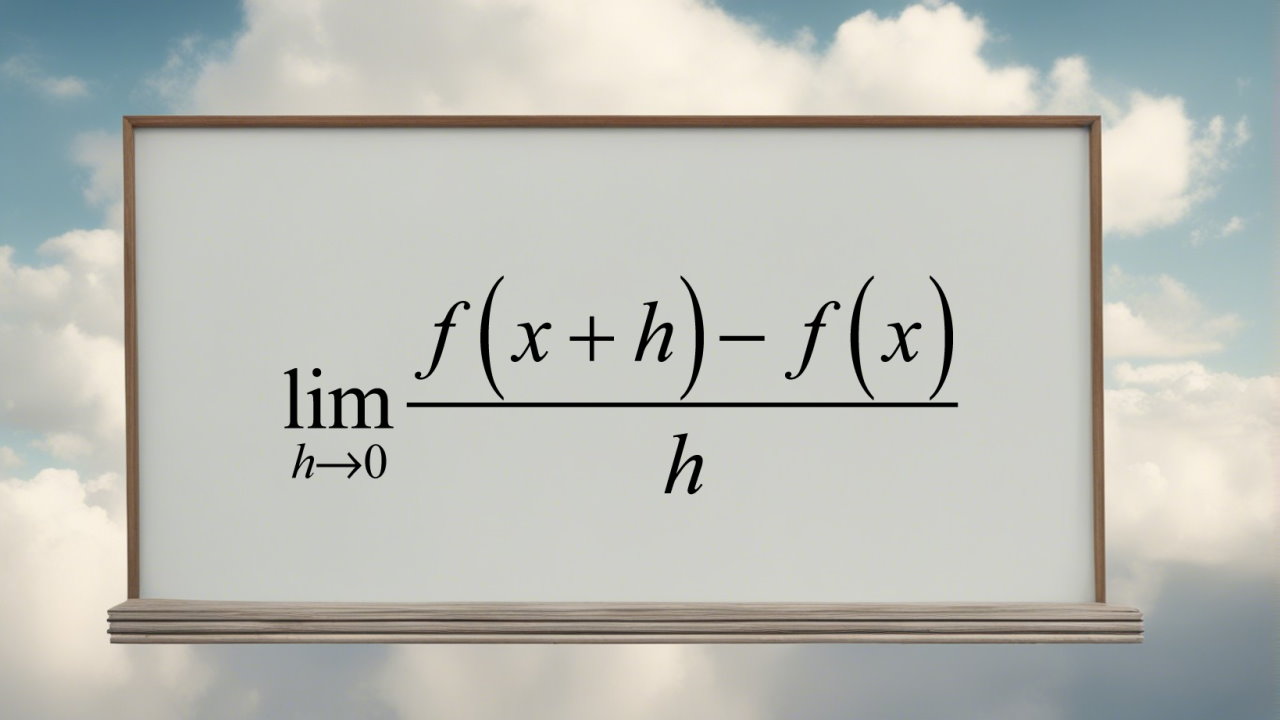
مشتق چیست ؟
«مشتق» (Derivative)، نرخ تغییرات یک تابع نسبت به یک متغیر است.
اگر بخواهیم مشتق را به زبان سادهتر تعریف کنیم، میتوانیم بگوییم که این مفهوم ریاضی، شیب نمودار در یک نقطه را نمایش میدهد. برای درک بهتر مفهوم مشتق، نمودار زیر را در نظر بگیرید.

شیب نمودار (خط سبز) در تصویر بالا، از تقسیم تغییرات Y بر تغییرات X به دست میآید:
تغییرات X ÷ تغییرات Y = شیب
شیب میانگین بین دو نقطه از یک نمودار نیز با استفاده از رابطه بالا به دست میآید. به عنوان مثال، نمودار زیر را به همراه اعداد نمایش داده شده در نظر بگیرید.
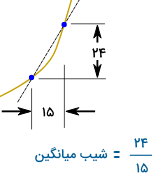
دو نقطه مشخص شده بر روی نمودار، در راستای Y و X با یکدیگر اختلاف دارند. با تقسیم اختلاف در راستای Y بر اختلاف در راستای X، شیب میانگین بین این دو نقطه به دست میآید. در صورت نزدیکی خیلی زیاد دو نقطه به یکدیگر، اختلاف آنها در هر دو راستا، تقریبا برابر با صفر میشد.
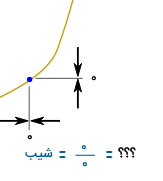
در مثال بالا، چیزی برای اندازهگیری وجود ندارد. با این حال، اگر دو نقطه را از نمای بسیار نزدیک نگاه کنیم، اختلاف جزئی بین آنها نمایان میشود. در ریاضیات، این اختلافهای جزئی را با Δ نمایش میدهند.
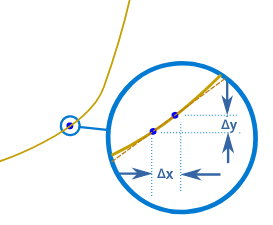
اکنون میتوانیم شیب میانگین بین دو نقطه را به دست بیاوریم. این شیب، عبارت است از:
m، علامت مورد استفاده برای نشان دادن شیب در روابط ریاضی است. اکنون میتوانیم از این رابطه برای گرفتن مشتق توابع استفاده کنیم. تابع زیر را در نظر بگیرید:
برای به دست آوردن مشتق تابع بالا، دو نقطه بسیار نزدیک بر روی نمودار آن را در مشخص میکنیم.
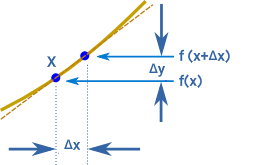
با توجه نمودار، اختلاف دو نقطه در راستای X از x تا x+Δx و اختلاف دو نقطه در راستای Y از f(x) تا f(x+Δx) است. برای به دست آوردن مشتق تابع، مراحل زیر را انجام میدهیم:
- قرار دادن تابع در فرمول
- سادهسازی و باز کردن عبارتها تا حد ممکن
- برابر قرار دادن Δx با صفر
مثال ۱: محاسبه مشتق تابع با فرمول شیب
مشتق تابع را به دست بیاورید.
تعیین مشتق تابع بالا، طی سه مرحله انجام میشود.
مرحله اول: قرار دادن تابع در فرمول شیب
فرمول محاسبه شیب دو نقطه نزدیک به هم در یک تابع عبارت است از:
برابر با x است. به این ترتیب، برابر با x + Δx میشود. با جایگذاری این عبارتها در فرمول شیب، خواهیم داشت:
مرحله دوم: ساده سازی عبارت ها
به این ترتیب، مشتق x برابر با ۱ شد. از آنجایی که پس از سادهسازی، عبارت Δx، باقی نماند، نیازی به انجام مرحله سوم (صفر کردن Δx) نبود.
تمرین و آزمون
علائم مشتق در ریاضیات
در ریاضیات، مشتق تابع f(x) را با f'(x) نمایش میدهند. برای نشان دادن «Δx به سمت صفر» نیز از عبارت dx استفاده میکنند. به عنوان مثال، برای مشتق داریم:
تمرین و آزمون
قانون مشتق اعداد ثابت
مشتق تمام اعداد برابر با صفر است. اعداد، معرف یک نقطه ثابت هستند. مطابق با تعریف، مشتق، نرخ تغییرات تابع را نمایش میدهد. اعداد ثابت، هیچ تغییری ندارند. بنابراین، مشتق آنها برابر با صفر در نظر گرفته میشود. فرم ریاضی این قانون مشتق اعداد ثابت عبارت است از:
در فرمولهای ریاضی، اعداد ثابت را با c یا C (ابتدای کلمه Constant به معنای ثابت) نمایش میدهند.
تمرین و آزمون
در این بخش، اصول مشتقگیری از توابع را مورد بررسی قرار دادیم و یک روش پایهای برای تعیین مشتق ارائه کردیم. در حالت کلی، نیازی به استفاده از مفهوم شیب برای مشتقگیری نیست. توابع مختلف، فرمول های مشتق مختص به خود را دارند.
دانلود فایل فرمول های مهم مشتق
مراحل بالا، روند اثبات مشتق یک تابع با حد و پیوستگی هستند. مجله فرادرس، خلاصهای از فرمول های مهم مبحث مشتق را در یک فایل PDF جمعآوری کرده است. لینک دانلود این فایل در ادامه آورده شده است.
- برای دانلود تقلب نامه (Cheat Sheet) فرمول های مشتق گیری + اینجا کلیک کنید.

فرمول های مشتق چند جمله ای ها
چندجملهای، عبارتی متشکل از متغیرها، ضرایب عددی و عملگرها است. از سادهترین انواع چندجملهایها میتوان به عبارتهای تکجملهای اشاره کرد. در بخشهای قبلی، چندین تکجملهای را مشاهده کردیم. این عبارتهای ریاضی، از یک عبارت (متغیرها و ضرایب عددی) تشکیل میشوند.
فرمول مشتق چند جمله ای های توان دار
مشتق تکجملهایها از قانونی با عنوان «قانون توان» پیروی میکند. فرمول ریاضی این قانون عبارت است از:
برای اینکه از یک تکجملهای مشتق بگیریم، ابتدا توان آن را به صورت ضریب به پشت متغیر انتقال میدهیم و سپس به اندازه یک واحد از توان قبلی متغیر کم میکنیم. به عنوان مثال، بر اساس قانون بالا، مشتق عبارت برابر با میشود.
فرمول مشتق چند جمله ای ها با ضریب ثابت
یکی دیگر از قانونهای مورد استفاده برای نوشتن فرمول های مشتق، قانون ضریب ثابت است. بر اساس این قانون، پس از مشتقگیری، ضریب پشت متغیر تغییر نمیکند. فرمول ریاضی قانون ضریب ثابت در مشتق چندجملهایها به صورت زیر نوشته میشود:
رابطه بالا را میتوانیم به شکل زیر نیز بنویسیم:
مثال ۲: تعیین مشتق عبارت تک جمله ای
مشتق عبارت را به دست بیاورید.
عبارت مورد سوال، یک تکجملهای است. مشتق تکجملهایها از رابطه زیر به دست میآید:
عبارت را درون رابطه بالا قرار میدهیم:

در اینجا، ضریب c برابر با ۴ است. بنابراین، این عدد را در پشت متغیر x ضرب کرده و ۱ واحد از آن کم میکنیم:
در نتیجه، مشتق برابر با است.
تمرین و آزمون
فرمول های مشتق جمع و تفریق توابع و چند جمله ای ها
در بخشهای قبلی، فرمول های مشتق تکجملهایها را مرور کردیم. در صورتی که دو یا چند تکجملهای، جمع و یا تفریق شوند، یک چندجملهای تشکیل میشود. برای به دست آوردن مشتق چندجملهایها، مشتق هر عبارت را به صورت جداگانه تعیین میکنیم؛ اما علائم جمع و تفریق را تغییر نمیدهیم. فرمول ریاضی قانون جمع و تفریق در مشتق چندجملهایها عبارت است از:
قانون توان، قانون ضریب ثابت و دیگر قانونهای مشتقگیری، برای هر یک از جملههای چندجملهای صادق هستند. نحوه استفاده از این قانون را با حل یک مثال توضیح میدهیم.
مثال ۳: محاسبه مشتق تابع چند جمله ای
مشتق تابع را به دست بیاورید.
تابع چندجملهای مورد سوال، از سه عبارت زیر تشکیل میشود:
- عبارت متغیر توانی
- عبارت متغیر
- عبارت ثابت عددی ۴
برای به دست آوردن مشق تابع، مشتق هر یک از عبارتهای بالا را به دست میآوریم:
اکنون، به جای هر یک از عبارتها، مشتق آنها را درون تابع مشتق قرار میدهیم:
به این ترتیب، مشتق تابع چندجملهای به دست آمد.
تمرین و آزمون

فرمول های مشتق ضرب توابع و چند جمله ای ها
محاسبه مشتق ضرب چندجملهایها، روشهای مختلفی دارد. یکی از این روشها، انجام ضرب و تعیین مشتق هر یک از عبارتها است. روش دیگر، با عنوان «قانون ضرب در مشتق چندجملهایها» شناخته میشود. فرمول ریاضی این قانون عبارت است از:
به عبارت دیگر، مشتق حاصلضرب دو تابع، برابر با ضرب تابع اول در مشتق تابع دوم به علاوه ضرب تابع دوم در مشتق تابع اول است.
مثال ۴: محاسبه مشتق ضرب دو چند جمله ای
مشتق تابع را به دست بیاورید.
تابع f(x)، حاصلضرب دو چندجملهای است. برای به دست آوردن مشتق این تابع، ابتدا هر یک از این چندجملهایها را برابر با یک تابع مستقل در نظر میگیریم:
به این ترتیب:
مطابق با فرمول مشتق ضرب چندجملهایها، داریم:
برای حل رابطه بالا، به مشتق توابع u(x) و v(x) را تعیین میکنیم:
اکنون توابع u(x) و v(x) و مشتق آنها را درون رابطه مشتق f(x) قرار میدهیم:
به این ترتیب، مشتق ضرب دو چندجملهای را به دست آوردیم. در این مثال، میتوانستیم دو چندجملهای را ابتدا در یکدیگر ضرب کرده و سپس مشتق حاصلضرب را تعیین کنیم. استفاده از هر دوی این روشها، نتیجه یکسانی دارد. با این وجود، سرعت رسیدن به جواب در مسائل مختلف متفاوت است.
مجله فرادرس، خلاصهای از فرمول های مهم مبحث مشتق را در یک فایل PDF جمعآوری کرده است. لینک دانلود این فایل در ادامه آورده شده است.
- برای دانلود تقلب نامه (Cheat Sheet) فرمول های مشتق گیری + اینجا کلیک کنید.
فرمول های مشتق توابع کسری و تقسیم چند جمله ای ها
فرمول مشتق تقسیم چندجملهایها و توابع کسری، به صورت زیر نوشته میشود:
در مبحث مشتق، به رابطه بالا، «قانون تقسیم» میگویند. برای درک بهتر این رابطه، به حل یک مثال و تمرین میپردازیم.
برای درک بهتر نحوه استفاده از فرمول های مشتق توابع کسری، در ادامه به حل یک مثال و تمرین به همراه جدول قوانین رایج مشتقگیری میپردازیم.

مثال ۵: محاسبه مشتق تقسیم چند جمله ای
مشتق را تعیین کنید.
برای به دست آوردن مشتق تابع مورد سوال، صورت و مخرج آن را به عنوان دو تابع جدا در نظر میگیریم:
اکنون میتوانیم تابع f(x) را به صورت زیر بنویسیم:
بر اساس قانون تقسیم در مشتق، داریم:
به این ترتیب، باید مشتق توابع u(x) و v(x) را تعیین کنیم:
توابع u(x) و v(x) را به همراه مشتقشان درون قانون تقسیم قرار میدهیم:
در نتبجه مشتق تابع کسری f(x) برابر با شد.
تمرین و آزمون
جدول ویژگی ها و فرمول های مشتق
اغلب فرمول های مشتق که در بخشهای قبلی به معرفی آنها پرداختیم، با عنوان قوانین مشتقگیری شناخته میشوند. جدول زیر، خلاصهای از این قوانین را نمایش میدهد.
| قانون مشتقگیری | فرمول مشتقگیری |
|---|---|
| قانون عدد ثابت | |
| قانون ضریب ثابت | |
| قانون توان | |
| قانون جمع | |
| قانون تفریق | |
| قانون ضرب | |
| قانون تقسیم | |
| قانون زنجیرهای |

فرمول های مشتق توابع مثلثاتی
توابع مثلثاتی، توابعی هستند که رابطه بین زوایای داخلی و ضلعهای مثلث قائم الزاویه را نمایش میدهند. سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت، به عنوان توابع مثلثاتی اصلی شناخته میشوند. مهمترین فرمول های مشتق توابع مثلثاتی در جدول زیر آورده شدهاند:
| تابع مثلثاتی | مشتق تابع مثلثاتی |
|---|---|
فرمول های مشتق توابع مثلثاتی برای کاربردهای متعددی نظیر تعیین شیب خطوط مماس و قائم بر منحنی، تعیین معادله خطوط مماس و قائم بر منحنی، تعیین مقادیر حداقلی و حداکثری توابع خاص و غیره مورد استفاده قرار میگیرند. این فرمولها، در حوزههای مختلفی نظیر الکترونیک، برنامهنویسی، مدلسازی، مهندسی و غیره کاربرد دارند.
برای درک بهتر نحوه استفاده از فرمول های مشتق توابع مثلثاتی، در ادامه به حل یک مثال و تمرین میپردازیم.
مثال ۶: تعیین مشتق ضرب توابع مثلثاتی
مشتق تابع را به دست بیاورید.
به منظور تعیین مشتق تابع مورد سوال، از قانون ضرب در مشتق استفاده میکنیم. این قانون به صورت زیر نوشته میشود:
در رابطه بالا، داریم:
مشتق f(x) برابر است با:
مشتق تابع g(x)، مطابق با قانون زنجیرهای عبارت است از:
مشتقهای به دست آمده را درون رابطه قانون ضرب قرار میدهیم:
تمرین و آزمون
فرمول های مشتق توابع هیپربولیک
توابع هذلولی یا هیپربولیک، معادل توابع مثلثاتی معمولی هستند که به جای معادلات دایره، توسط معادلات هذلولی تعریف میشوند. سینوس هیپربولیک (sinh)، کسینوس هیپربولیک (cosh)، تانژانت هیپربولیک (tanh)، کتانژانت هیپربولیک (coth)، سکانت هیپربولیک (sech) و کسکانت هیپربولیک (csch)، به عنوان توابع هذلولی اصلی در نظر گرفته میشود. فرمول های مشتق این توابع در جدول زیر آورده شدهاند.
| تابع هیپربولیک | مشتق تابع هیپربولیک |
در صورت معکوس کردن توابع مثلثاتی و هذلولی، مشتق آنها به شکل یک تابع کسری درمیآید. در بخشهای بعدی، راجع به فرمول های مشتق توابع معکوس صحبت خواهیم کرد.
فرمول های مشتق توابع معکوس
تابع معکوس یا معکوس تابع، عبارتی است که با گرفتن خروجی تابع، ورودی آن را به ما میدهد. در واقع، در تابع معکوس، عنوان خروجی و ورودی عوض میشود. اگر توابع f(x) و g(x) معکوس یکدیگر باشند، رابطه تعیین مشتق آنها (فرمول مشتق توابع مکعوس) برابر خواهد بود با:
برای درک بهتر نحوه استفاده از فرمول های مشتق توابع معکوس، در ادامه به حل یک مثال و تمرین میپردازیم.

مثال ۷: تعیین مشتق معکوس تابع
توابع و ، معکوس یکدیگر هستند. مشتق تابع g(x) را به دست بیاورید.
بر اساس رابطه مشتق تابع معکوس، داریم:
مشتق تابع f(x) برابر است با:
به این ترتیب، f'(g(x)) برابر میشود با:
$$ f’ ( g ( x ) ) = ۳ ( \sqrt [ \leftroot { 1 } \uproot { 4 } ۳ ] { x } ) ^ ۲ = ۳ x ^ { \frac { ۲ } { ۳ } } $$
با قرار دادن نتیجه بالا در رابطه مشتق معکوس تابع، خواهیم داشت:
در این مثال، میتوانستیم مشتق را با استفاده قانون ضرب نیز تعیین کنیم. برای این کار، فرم توانی تابع g(x) را در نظر میگیریم:
بر اساس قانون توان در مشتق داریم:
به این ترتیب:
جواب مشتق هر دو روش، یکسان است.
تمرین و آزمون
فرمول های مشتق توابع معکوس مثلثاتی
توابع معکوس مثلثاتی، توابعی هستند که با گرفتن مقدار خروجی، مقدار ورودی تابع مثلثاتی را به دست میآورند. به زبان سادهتر و به عنوان مثال، اگر بخواهیم بفهیم سینوس چه زاویهای برابر با ۰/۵ میشود، از معکوس تابع سینوس یا اصطلاحا تابع آرکسینوس استفاده میکنیم. توابع معکوس، را با توان (۱-) نمایش میدهند:
فرمول های مشتق توابع معکوس مثلثاتی، در جدول زیر آورده شدهاند. این فرمولها، با توجه به رابطه کلی مشتق توابع معکوس به دست آمدهاند.
| تابع معکوس مثلثاتی | مشتق تابع معکوس مثلثاتی |
برای آشنایی بیشتر با فرمول های مشتق در جدول بالا، مطالعه مطلب زیر را به شما پیشنهاد میکنیم.
فرمول های مشتق معکوس توابع هذلولی
بر اساس رابطه مشتق توابع معکوس، فرمول های مشتق معکوس توابع هذلولی نیز به شکل توابع کسری درمیآیند. جدول زیر، این فرمولها را نمایش میدهد.
| معکوس تابع هذلولی | مشتق معکوس تابع هذلولی |

فرمول های قاعده زنجیره ای در مشتق گیری
قاعده زنجیرهای، به منظور مشتقگیری از توابع تو در تو مورد استفاده قرار میگیرد. فرمول این قاعده عبارت است از:
علاوه بر فرمول بالا، یک فرمول دیگر برای تعیین مشتق توابع تو در تو وجود دارد. در این فرمول، u=x قرار میدهیم. به این ترتیب، رابطه مشتق به صورت زیر تغییر میکند:
برای درک بهتر نحوه استفاده از فرمول های قاعده زنجیرهای، در ادامه به حل یک مثال و تمرین به جدول روابط رایج در مشتقگیری از توابع تو در تو میپردازیم.
مثال ۸: محاسبه مشتق تابع زنجیره ای
مشتق تابع چیست؟
تابع ، یک تابع تو در تو محسوب میشود. در اینجا میتوانیم را به عنوان تابعی درون تابع سینوس در نظر بگیریم. به عبارت دیگر:
اکنون میخواهیم مشتق تابع را به دست بیاوریم. بر اساس فرمول مشتق قاعده زنجیرهای داریم:
عبارت اول، به صورت زیر تعیین میشود:
عبارت دوم نیز به صورت زیر به دست میآید:
عبارتهای بالا را درون فرمول اصلی قرار میدهیم:
با استفاده از تغییر متغیر نیز میتوانستیم به راحتی جواب مشتق تابع مورد سوال به دست بیاوریم. برای این کار، ابتدا تابع درونی ۲x را برابر با یک متغیر دلخواه مانند u و تابع اصلی f(x) را برابر با y در نظر میگیریم:
به این ترتیب، داریم:
اکنون از رابطه زیر برای تعیین مشتق استفاده میکنیم:
عبارت اول در این رابطه ()، به معنای مشتقگیری از تابع y بر حسب u است. حاصل این عبارت به صورت زیر تعیین میشود:
عبارت دوم ()، مشتق تابع u بر حسب x را نشان میدهد. حاصل این عبارت نیز به صورت زیر به دست میآید:
اکنون، مقادیر به دست آمده را درون رابطه اصلی قرار میدهیم:
عبارت u را به عبارت اولیه آن، یعنی ۲x بازمیگردانیم:
تمرین و آزمون

در جدول زیر، برخی از متداولترین فرمول های مشتق توابع زنجیرهای آورده شدهاند.
| تابع زنجیرهای | فرمول مشتق تابع زنجیرهای |
فرمول های مشتق مراتب بالاتر
به مشتقگیری مجدد از مشتق توابع، مشتق مراتب بالاتر میگویند. جدول زیر، روشهای مختلف مشتقهای مراتب بالاتر (تا مرتبه سوم) را نمایش میدهد. در این مشتقها، f(x)=y در نظر گرفته شده است.
| مشتق مرتبه اول | مشتق مرتبه دوم | مشتق مرتبه سوم |
به منظور به دست آوردن مشتق مراتب بالاتر، ابتدا مشتق مرتبه اول را تعیین میکنیم. با مشتقگیری از مشتق مرتبه اول، مشتق مرتبه دوم به دست میآید. تکرار این فرآیند، مشتق مرتبه سوم، چهارم و بالاتر را در پی دارد. در ادامه، فرآیند مشتقگیری مرتبه بالاتر را به یک مثال و تمرین توضیح میدهیم.
برای درک بهتر نحوه استفاده از فرمول های مشتق مراتب بالاتر، در ادامه به حل یک مثال و تمرین میپردازیم.
مثال ۹: تعیین مشتق مراتب بالاتر
مشتق مرتبه دوم تابع را به دست بیاورید.
صورت سوال، مشتق مرتبه دوم را از ما میخواهد. بنابراین، حل سوال، طی دو مرحله انجام میشود. مرحله اول، به دست آوردن اولین متشق از تابع f(x) یا همان f'(x) است:
به منظور تعیین مشتق مرتبه دوم f(x)، از f'(x)، مشتق میگیریم:
تمرین و آزمون
مجله فرادرس، خلاصهای از فرمول های مهم مبحث مشتق را در یک فایل PDF جمعآوری کرده است. لینک دانلود این فایل در ادامه آورده شده است.
- برای دانلود تقلب نامه (Cheat Sheet) فرمول های مشتق گیری + اینجا کلیک کنید.

فرمول های مشتق توابع پارامتری
تابع پارامتری، تابعی است که رابطه بین متغیرهای مختلف را بر حسب یک یا چند متغیر مستقل (پارامتر) بیان میکند. به عنوان مثال، دستگاه معادلات زیر را در نظر بگیرید:
در این دستگاه، دو متغیر x و y، به صورت تابعی از یک متغیر دیگر به نام t بیان شدهاند. در اینجا، به متغیر t، پارامتر و به توابع معرف رابطه بین x و y، تابع پارامتری میگویند. مشتق تابع y بر حسب x عبارت است از:
برای درک بهتر نحوه استفاده از فرمول های مشتق توابع پارامتری، در ادامه به حل یک مثال و تمرین میپردازیم.
مثال ۱۰: تعیین مشتق تابع پارامتری
مشتق تابع پارامتری زیر (مشتق y بر حسب x) را به دست بیاورید.
به منظور تعیین مشتق توابع پارامتری، از فرمول زیر استفاده میکنیم:
برای حل این فرمول، به مشتق x و y بر حسب t نیاز داریم:
در نتیجه:
تمرین و آزمون
آزمون فرمول های مشتق
۱. مشتق چگونه نرخ تغییر یک تابع و ارتباط آن با شیب نمودار را توضیح میدهد؟
مشتق همیشه برابر با مقدار ثابت تابع است.
مشتق نرخ تغییر تابع را نسبت به متغیر مستقل نشان میدهد و با شیب خط مماس بر نمودار تابع مرتبط است.
مشتق تنها برای توابع صعودی قابل استفاده است.
مشتق بیانگر مقدار تابع در نقطه خاص است.
مشتق نرخ تغییر تابع نسبت به متغیر را بیان میکند و معنای هندسی آن معادل شیب خط مماس بر نمودار در هر نقطه است. این ویژگی باعث میشود با استفاده از مشتق بتوان تغییرات لحظهای تابع و جهت روند آن را تحلیل کرد.
۲. در فرآیند مشتقگیری، تفاوت اصلی بین شیب میانگین و شیب آنی چیست و چرا استفاده از حد در این تمایز حیاتی است؟
شیب میانگین فقط وابسته به مشتق توابع نمایی است و شیب آنی مختص توابع خطی.
شیب میانگین تغییرات تابع را بر بازه بزرگ میسنجد اما شیب آنی با استفاده از حد، رفتار تابع را در نقطه دقیق بررسی میکند.
شیب میانگین همیشه ثابت است اما شیب آنی فقط برای توابع صعودی معنی دارد.
شیب میانگین نیاز به محاسبه حد ندارد ولی شیب آنی بدون وجود مشتق جزئی تعریف میشود.
شیب میانگین به اختلاف مقدار تابع بین دو نقطه نسبت به فاصله آنها اشاره دارد، در حالی که برای دستیابی به شیب آنی باید بازه را به سمت صفر میل داد و از مفهوم حد (Limit) کمک گرفت تا نرخ تغییر لحظهای در همان نقطه بدست آید.
۳. برای مشتقگیری به روش گام به گام، کدام توالی از مراحل زیر صحیح است؟
جایگذاری f(x) در فرمول شیب، سادهسازی عبارت و گرفتن حد برای Δx نزدیک به صفر
ابتدا محاسبه f(0)، سپس ضریب x را پیدا کردن و نتیجه را نوشتن
محاسبه مقدار مشتق با جدول، سپس تجزیه عددی و فرض تغییر بزرگ در x
استفاده مستقیم از قانون جمع، سپس قرار دادن x=0 و مقایسه نتیجه
در مشتقگیری تابع به روش گام به گام لازم است ابتدا تابع را در فرمول شیب قرار دهیم، سپس عبارت به دست آمده را ساده کنیم و در نهایت حد آن را برای Δx نزدیک به صفر محاسبه نماییم. این روش، همان روند آموزش داده شده برای مشتق توابع درجه دوم است و به درک فرآیند اصلی مشتقگیری کمک میکند.
۴. کدام مورد درباره نمادهای رایج مشتقگیری در ریاضیات درست است؟
و هر دو فقط برای توابع ثابت استفاده میشوند.
نماد همیشه برای مشتقگیری عدد ثابت استفاده میشود.
نماد مشتق کسری شکل فقط برای مشتق توابع معکوس است.
نماد عمدتا برای مشتق تابع نسبت به متغیر به کار میرود.
در مشتقگیری نماد برای نمایش مشتق تابع نسبت به یک متغیر رایج است و به شکل ساده با علامت ' نشان داده میشود. نماد مشتق کسرگونه () نیز برای همین منظور به کار میرود اما معمولا فرمت کسرگونه تفاوت نمایش را ایجاد میکند.
۵. مشتق کدام نوع تابع همیشه برابر با صفر است و علت این ویژگی از دیدگاه ریاضی چیست؟
توابع چندجملهای با توانهای مثبت
توابع عددی ثابت مانند f(x)=c
توابع کسری با مخرج متغیر
توابع مثلثاتی مانند sin(x)
«توابع عددی ثابت مانند f(x)=c» همیشه مشتقشان صفر است چون مقدار چنین تابعی صرفنظر از مقدار x تغییر نمیکند؛ یعنی نرخ تغییر آن صفر است. در حالی که «توابع چندجملهای با توانهای مثبت» و «توابع مثلثاتی مانند sin(x)» و همچنین «توابع کسری با مخرج متغیر»، مقادیرشان نسبت به x تغییر میکند و مشتق آنها صفر نیست.
۶. هنگام مشتقگیری از چندجملهایهایی با ضریب ثابت و تواندار، باید از کدام قاعده استفاده کنیم و چه عملی انجام میدهیم؟
فقط عدد ثابت را مشتق میگیریم و بقیه حذف میشوند.
هر دو ضریب و توان حذف میشوند و فقط متغیر باقی میماند.
توان را افزایش میدهیم و ضریب را نصف میکنیم.
ضریب را حفظ میکنیم و توان را یک واحد کم میکنیم.
در مشتقگیری از چندجملهایهایی که ضریب عددی دارند و به صورت x به توان n نوشته میشوند، قانون اصلی این است که ضریب را همانطور حفظ کرده و برای متغیر، توان را یک عدد کم میکنیم. نرخ تغییر فقط به تغییر توان وابسته است و ضریب تاثیر مستقیمی بر مشتق ندارد.
۷. کدام قانون مشتقگیری اجازه میدهد عبارات یک چندجملهای را به صورت جداگانه مشتق گرفته و نتیجه را جمع یا کم کنیم؟
قانون زنجیرهای
قانون جمع و تفریق در مشتقگیری
قانون تقسیم
قانون ضرب
قانون جمع و تفریق در مشتقگیری بیان میکند که هر عبارت داخل یک چندجملهای را میتوان مستقل مشتق گرفت و سپس جمع یا تفریق نتیجهها را بدون تغییر انجام داد. بنابراین این قانون محاسبات مشتق را برای چندجملهایها بسیار ساده میکند. قانون ضرب برای مشتق حاصلضرب دو تابع کاربرد دارد، قانون تقسیم برای مشتق توابع کسری استفاده میشود، و قانون زنجیرهای نیز برای مشتق توابع ترکیبی به کار میرود.
۸. اگر دو تابع را در هم ضرب کنیم و بخواهیم مشتق حاصل را به دست آوریم، از کدام قاعده باید استفاده کرد؟
قاعده ضرب که طبق آن مشتق ضرب، مجموع ضرب مشتق هر تابع در تابع دیگر است.
مشتقگیری هر تابع جداگانه و ضرب نتایج با هم
مشتقگیری هر تابع جداگانه و جمع آنها
مشتق تابع اول و دوم را با هم تقسیم و حاصل را ساده میکنیم.
قاعده ضرب بیان میکند که برای مشتقگیری از حاصلضرب دو تابع، باید مشتق هر تابع را به ترتیب در تابع دیگر ضرب و سپس مجموع این دو ضرب را به دست آورد.
۹. در هنگام مشتقگیری یک تابع کسری که صورت و مخرج آن چندجملهای باشند، ترتیب صحیح استفاده از قانون تقسیم مشتقگیری چگونه است؟
مشتق صورت را ضرب در مخرج و منهای صورت ضرب در مشتق مخرج کرده، نتیجه را بر مربع مخرج میگذاریم.
مشتق صورت را منهای مشتق مخرج کرده و حاصل را بر جمع صورت و مخرج قرار میدهیم.
مشتق صورت و مخرج را به صورت جداگانه تقسیم میکنیم و نتیجه همان مشتق کل تابع است.
ابتدا مشتق صورت و سپس مشتق مخرج را جداگانه گرفته، سپس تقسیم میکنیم.
در قانون تقسیم مشتق، باید ابتدا مشتق صورت را در مخرج ضرب کنیم و از آن، ضرب صورت در مشتق مخرج را کم کنیم؛ سپس کل عبارت را بر مربع مخرج قرار دهیم. این روش باعث میشود مشتق درست تابع کسری محاسبه گردد.
۱۰. برای مشتقگیری از ضرب توابع مثلثاتی مانند sin(x) و cos(2x)، چه قواعدی مورد نیاز است؟
قانون مشتق ضرب و قاعده زنجیره ای
قانون مشتق تقسیم و مشتق ثابت
فقط قانون جمع و تفریق مشتقها
فقط قانون مشتق ضرب
برای مشتقگیری ضرب توابعی مانند sin(x) و cos(2x)، باید هم از «قانون مشتق ضرب» برای محاسبه مشتق حاصلضرب دو تابع و هم از «قاعده زنجیرهای» برای مشتقگیری از تابعی مانند cos(2x) که داخل آن متغیر دیگری دارد، استفاده کرد.
۱۱. برای محاسبه مشتق مرتبه دوم یا بالاتر یک تابع چندجملهای، چه مراحلی اجرا میشود و با چه نمادهایی این مراتب نمایش داده میشوند؟
مشتق مرتبه دوم مستقیما با تقسیم ضریبها بر دو به دست میآید و از نماد استفاده میشود.
ابتدا مشتق اول گرفته شده و سپس همین روند تکرار و هر بار از نمادهای یا استفاده میشود.
فقط برای مرتبه اول و دوم مشتقگیری امکانپذیر است و باید هر کدام را با نماد حرفی جدا بیان کرد.
تمام مرتبههای مشتق فقط با نماد نوشته میشوند و کافی است یک بار مشتق بگیریم.
در محاسبه مشتق مرتبه دوم و بالاتر یک تابع چندجملهای، ابتدا مشتق اول تابع را میگیریم و سپس همین روند را بر روی نتیجه ادامه میدهیم تا به مرتبه دلخواه برسیم. هر مشتق جدید با افزودن یک علامت پریم نمایش داده میشود.
۱۲. برای یافتن مشتق تابع پارامتری y(t) نسبت به x که x نیز بر حسب t تعریف شده است، کدام رابطه باید استفاده شود؟
مشتق y نسبت به t را با مشتق x نسبت به y جمع کنیم.
ابتدا y را نسبت به x مشتق بگیریم و متغیر t را کنار بگذاریم.
مشتق معمول y نسبت به t را بر مشتق x نسبت به t تقسیم کنیم.
مشتق y نسبت به x را برابر با t قرار دهیم.
وقتی هر دو تابع x(t) و y(t) بر حسب t تعریف شدهاند، مشتق y نسبت به x از تقسیم مشتق y نسبت به t بر مشتق x نسبت به t به دست میآید. این رابطه باعث میشود تغییرات y بر حسب x با توجه به پارامتر مشترک محاسبه شود.













در تستی که بعد از مثال شماره پنج اومده . باید مشتق صورت در مخرج ضرب بشه و منهای مشتق مخرج در صورت بشه . اما چرا مشتق صورت به جای اینکه در x²(مخرج) ضرب بشه در x ضرب شده؟
با سلام خدمت شما؛
نکته بیان شده کاملا صحیح است و اصلاحات لازم در پاسخ سوال اعمال شدند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
خیلی ممنون بسیار مفید بود
سلام وقت بخیر با تشکر از توضیح کاملی که در خصوص مشتق ارائه کردید. ذکر دو نکته را واجب دیدم:
1. در تست مربوط به محاسبه مشتق تابع چند جمله ای که زیر مثال 3 آورده شده است گزینه درست وجود ندارد.
2. همچنین در تست مربوط به مشتق تابع پارامتری زیر مثال 10 جای صورت و مخرج را اشتباه جایگذاری کرده اید.
با سلام و وقت بخیر؛
فرمولها اصلاح شدند. ممنون از توجه شما.
از همراهیتان با مجله فرادرس سپاسگزاریم.
در جدول مشتق های معکوس توابع هایپربولیک اشتباهی صورت گرفته.
سلام و عرض ادب خدمت عزیزان فرادرس بنده به عنوان دبیر ریاضی از مطالب بالا بسیار بهره بردم ممنون از لطفتان
با سلام؛
از ارائه بازخورد شما سپاسگزار و خوشحالیم که مطالعه این مطلب برای شما مفید بوده است.
با تشکر از همراهی شما با مجله فرادرس
سلام و وقت بخیر؛
نمایش فرمولها اصلاح شد. خیلی ممنون از توجه شما.
از همراهی شما با مجله فرادرس سپاسگزاریم.