شناسایی داده پرت در SPSS – راهنمای کاربردی
اصول و روشهای آماری وابسته به رفتار جامعه آماری و بخصوص اکثریت اعضای آن بنا نهاده شده است. بیشتر شاخصهای آماری، مانند میانگین و انحراف معیار، که برای توصیف چنین جامعهای به کار میرود، براساس همه مشاهدات، محاسبه شده و تحت تاثیر مقادیر آنها هستند. به همین دلیل وجود «داده پرت» (Outlier Data) یا دورافتاده، که ممکن است براثر خطا اندازهگیری بوجود آمده یا واقعا از اعضای استثنایی جامعه باشند، این شاخصها را به شدت تحت تاثیر قرار میدهند. در این نوشتار به شیوههای مختلف شناسایی داده پرت در SPSS میپردازیم تا نتایج حاصل از تحلیلهای آماری را اعتبار بیشتری ببخشیم.


به منظور آشنایی بیشتر با موضوع این نوشتار بهتر است مطالب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و رسم نمودار در SPSS — راهنمای کاربردی را مطالعه کنید. همچنین خواندن تشخیص ناهنجاری (Anomaly Detection) — به زبان ساده و مشاهده ناهنجار و شناسایی آن در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.
شناسایی داده پرت در SPSS
«داده پرت» (Outiler) به مشاهداتی گویند که نسبت به یک نقطه مرکزی (مثل میانگین) فاصله زیادی برحسب یک شاخص پراکندگی (مثال انحراف معیار) داشته باشد. این ایده از خصوصیات توزیع نرمال گرفته شده است. در صورتی که دادهها دارای توزیع نرمال یا طبیعی باشند، احتمال اینکه مقداری خارج از فاصله سه برابر انحراف معیار از میانگین قرار گیرد، بسیار کوچک خواهد بود. در نتیجه اگر به چنین مشاهدهای برخوردیم، آن را داده پرت و در نتیجه مشاهده ناهنجار یا نامتعارف تلقی خواهیم کرد.
شناسایی داده پرت بر اساس توزیع نرمال
در تصویر زیر یک نمودار مربوط به متغیر تصادفی با «توزیع نرمال» (Normal Distribution) را مشاهده میکنید. همانطور که مشخص است، برای چنین مقادیری، شانس یا احتمال اینکه نقطهای خارج از سه انحراف استاندارد از میانگین فاصله داشته باشد تقریبا برابر با حدود 99.7 درصد است. در نتیجه در بین ۱۰۰۰ مشاهده فقط 3 خارج از این ناحیه قرار میگیرد. به این ترتیب اگر تعداد نقاط مربوط به تحلیل، کمتر از ۱۰۰۰ مشاهده باشد، انتظار داریم که نقاطی که خارج از ناحیه سه انحراف استاندارد از میانگین قرار میگیرند، داده پرت باشند.
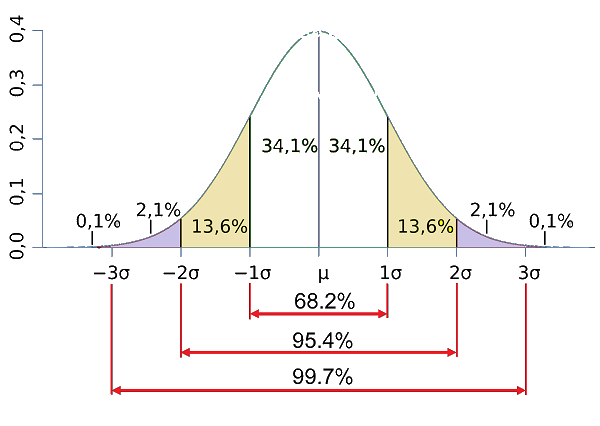
به این ترتیب یک روش برای تشخیص دادههای پرت، رسم نمودار فراوانی یا محاسبه فاصله نقطهها از میانگین و مقایسه آن سه برابر انحراف معیار است. همچنین میتوان مقدار نقطه را با مقدار است. اگر مقدار یک مشاهده از بزرگتر یا کوچکتر بود، آن را نقطه پرت در نظر میگیریم. وجود دادههای پرت، در نمودار فراوانی ممکن است باعث بروز «چولگی» (Skewness) شود.
مثال ۱: فرض کنید جدولی به صورت زیر از مقادیر مربوط به ۱۱ مشاهده در اختیار شما قرار گرفته است. در سطر دوم جدول ۱، فراوانی هر یک از مقادیر مشخص شده است.
جدول ۱: جدول فراوانی ۱۱ مشاهده
| مقدار () | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
| فراوانی () | 2 | 10 | 12 | 15 | 30 | 18 | 12 | 8 | 5 | 2 | 1 |
با توجه به این «جدول فراوانی» (Frequency Table)، «میانگین» (Mean) و «واریانس» (Variance) یا «انحراف معیار» (Standard Deviation) این دادهها طبق رابطه زیر محاسبه میشود.
در نتیجه کرانهای بالایی و پایینی برای چنین توزیعی به صورت زیر در خواهد آمد.
رابطه محاسبه کرانهای بالا و پایین برای مجموعه داده مربوط به جدول ۱ به صورت زیر در خواهد آمد.
بنابراین محدوده سه سیگما فاصله از میانگین در حدود نوشته خواهد شد. از آنجایی که آخرین نقطه یعنی ، خارج از این ناحیه قرار دارد، آن را به عنوان یک نقطه پرت شناسایی میکنیم.
نمودار مربوط به فراوانی نقاط جدول ۱، در نموداری که در تصویر ۲، قرار گرفته، دیده میشود.
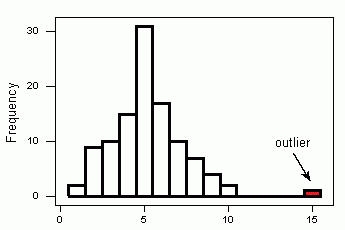
ممکن است همین کار بطور مستقیم و با کمک گرفتن از یک «نمودار فراوانی» (Histogram) نیز انجام شود. اگر نقطهای با فراوانی بسیار اندک و البته دور از بقیه نقاط قرار گرفته باشد، نقطه پرت شناخته خواهد شد. در هیستوگرام مشخص شده در تصویر 3 مشخص است که نقطهای که فراوانی آن با رنگ زرد مشخص شده یک نقطه پرت شناخته میشود زیرا نسبت به بقیه نقاط فاصله زیادی دارد.
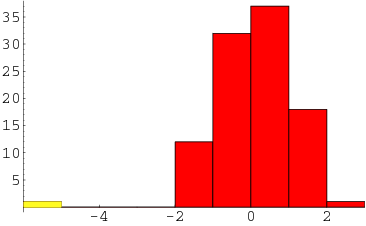
شناسایی داده پرت در SPSS با نمودارهای کنترل کیفی آماری
ممکن است پدیدههایی که وابسته به زمان هستند به منظور شناسایی داده پرت مورد تجزیه و تحلیل قرار گیرند. در نتیجه اندیس زمان مربوط به هر یک از مشاهدات را میتوان روی محور افقی نمودارها ترسیم کرد. شبیه این گونه نمودارها، در کنترل کیفی آماری به کار میرود.
محور افقی شماره نمونهها است که برحسب زمان مرتب شدهاند و محور عمودی نیز مشخصه کمی است که برای هر مشاهده اندازهگیری شده است. با محاسبه میانگین و انحراف معیار و رسم خطوط سه انحراف معیار معروف به سه سیگما، نواحی حول میانگین به شش بخش تقسیم میشود. مقادیری که بیش از سه انحراف معیار از میانگین (چه از بالا و چه از پایین) فاصله داشته باشند، نقطه پرت و به اصطلاح کنترل کیفی، مقدار خارج از کنترل نامیده میشود.
در تصویر زیر یک نمودار کنترل کیفی برای مقایسه میانگین فرآیند تولید یک قطعه دیده میشود. همانطور که میبینید نقطه یا مشاهده شماره 11، که به رنگ قرمز مشخص شده، خارج از کنترل بوده و داده پرت محسوب میشود.
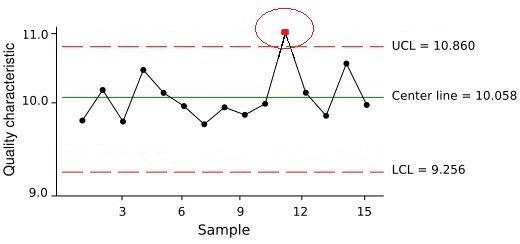
همانطور که مشاهده میکنید، این نمودار شبیه به نمودارهایی است که برای نمایش در کنترل بودن فرآیندها در حوزه کنترل کیفیت آماری ترسیم میشود. حدود بالایی (UCL) و پایینی (LCL) براساس سه انحراف معیار فاصله از میانگین ترسیم شدهاند. حروف UCL مخفف Upper Control Limit یا «کران بالای کنترل» و LCL نیز مخفف Lower Control Limit یا «کران پایین کنترل» است.
البته در مباحث کنترل کیفی، برای نمایش میزان پراکندگی فرآیند نیز نموداری مشابه به کار گرفته میشود که از آن هم برای نمایش نقاط خارج از کنترل میتوان استفاده کرد. برای مشاهده نحوه ترسیم نمودارهای کنترل کیفیت بهتر است نوشتار کنترل کیفیت آماری (Statistical Quality Control) — مفاهیم و نمودارهای کنترل را مطالعه کنید.
شناسایی داده پرت بر اساس شاخصهای ناپارامتری تمرکز و پراکندگی
همانطور که میدانید بسیاری از پدیدههای تصادفی در دنیای واقعی وجود دارند که از توزیع نرمال پیروی نمیکنند. در نتیجه بهتر است به جای استفاده از میانگین و انحراف معیار از برآوردهایی نسبتا پایدار (Robust) آنها یعنی میانه (Median) و دامنه چارکی (Inter-quartile Range) را برای شناسایی داده پرت استفاده کنیم. هر یک از این شاخصها به ترتیب به عنوان برآورد نقطه تمرکز و پراکندگی در روشهای ناپارامتری به کار میروند. بنابراین میتوانیم قاعدهای برای شناسایی داده پرت به این ترتیب پیدا کنیم که اگر نقطهای از سه برابر دامنه چارکی از چارک اول یا سوم دور باشد، آن را داده پرت بشناسیم.
نکته: برای محاسبه چندکها، ابتدا باید دادهها را از کوچک به بزرگ، مرتب کرده، سپس به محاسبه چندکها بپردازید. همچنین توجه داشته باشید که منظور از مشاهده ام بعد از مرتبسازی است.
محاسبه چندکها را براساس رابطه زیر انجام میدهیم.
که در آن
علامت به معنی جزء صحیح است. همچنین مقدار نیز به شکل زیر محاسبه میشود.
بنابراین برای محاسبه چارک اول و سوم کافی است که مقدار را برابر و تعیین کنیم، سپس مقادیر را بدست آوریم. دامنه میان چارکی نیز به شکل زیر محاسبه خواهد شد.
به این ترتیب محدوده مقادیری که به عنوان مجاز و با معنی در نظر گرفته میشوند، در فاصله سه IQR از چارک اول و سوم قرار میگیرد.
مثال ۲: براساس دادههای مربوط به مثال ۱، عمل میکنیم. چارک اول و سوم براساس جدول ۱، به صورت زیر محاسبه میشوند.
به این ترتیب مقدار چارک اول و سوم برابر خواهد بود با:
با توجه به محاسبات صورت گرفته، دامنه میان چارکی برابر با خواهد بود. کرانها نیز بر این اساس به شکل زیر در خواهند آمد.
در نتیجه مقدار مقدار دورافتاده یا پرت محسوب میشود. البته گاهی این معیار را سختگیرانهتر انتخاب کرده و فاصله از چارک اول و سوم را برابر با ۱٫۵ برابر دامنه چارکی در نظر میگیرند. در این حالت خواهیم داشت:
در بازه ارائه شده، مشخص است که مشاهدات 11 و ۱0 و ۹ با مقادیر نیز به عنوان نقاط پرت شناسایی خواهند شد.
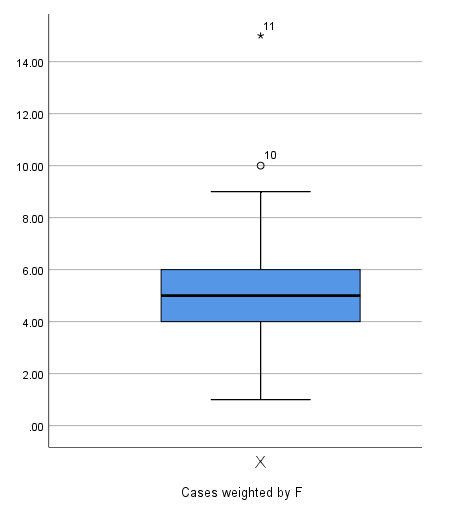
این شاخصها روی «نمودار جعبهای» (Boxplot) به خوبی نمایش داده میشوند. برای مشخص کردن چنین وضعیتی میتوانید یک «نمودار جعبهای» (Boxplot) نیز ترسیم کنید. نمونه یک نمودار جعبهای برای دادههای مربوط به جدول ۱ در تصویر ۵ دیده میشود. دایره و ستارهای که روی نمودار دیده میشود، نشانگر دادههای پرت است که علامت دایره برای فاصله یک و نیم برابر دامنه نیم چارکی مشخص شده و ستاره (*) نیز به کمک ۳ برابر فاصله دامنه نیم چارکی از چارک سوم تشکیل شده است.
نحوه رسم نمودارها در SPSS
از رسم نمودار جعبهای برای شناسایی داده پرت بخصوص زمانی که مشاهدات به صورت یک بُعدی باشند، به بهترین وجه میتوان استفاده کرد. ولی زمانی که با مشاهداتی با چند متغیر مواجه هستیم، استفاده از نمودار جعبهای و تشخیص نقاط نامتعارف براساس بررسی جداگانه متغیرها ممکن است نادرست به نظر آید. در این بین شیوههای تشخیص دادههای نامعمول و ناهنجار متفاوت خواهد بود. برای انجام این کار برای مشاهدات چند متغیره در محیط SPSS بهتر است، مطلب مشاهده ناهنجار و شناسایی آن در SPSS — راهنمای کاربردی را مطالعه کنید.
در این قسمت نحوه ترسیم یک نمودار جعبهای را به منظور شناسایی دادههای پرت معرفی میکنیم. مجموعه دادههای مربوط به مثال ۱ را در نظر بگیرید که در SPSS در پنجره Data Editor دیده میشود.
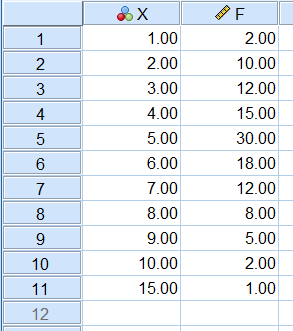
از آنجایی که ستون یا متغیر F، نشان دهنده تکرار یا فراوانی هر یک از مقادیر مربوط به ستون X است، باید SPSS را از این موضوع (وزندهی مشاهدات) مطلع کنیم. به این ترتیب از فهرست Data گزینه Weight Cases را اجرا میکنیم. در پنجرهای که مطابق با تصویر ۷ است، تنظیمات را اجرا میکنیم.
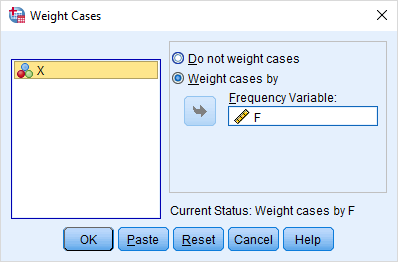
به این ترتیب، هر یک از مشاهدات براساس مقداری که در ستون F قرار گرفته، در محاسبات به صورت تکراری در نظر گرفته میشوند. حال به نحوه ترسیم نمودار جعبهای خواهیم پرداخت تا به کمک آن شناسایی داده پرت را انجام دهیم.
- از فهرست Graph گزینه Chart Builder را انتخاب کنید. سپس دکمه OK را بزنید.
- از داخل کادر Variables، متغیر X را با کلیک راست انتخاب کرده و گزینه Scale را فعال کنید تا SPSS متوجه شود که این متغیر از نوع مقیاس بوده و دارای مقادیر کمی و عددی است. در غیر اینصورت ممکن است نمودار ترسیم شده، صحیح نباشد.
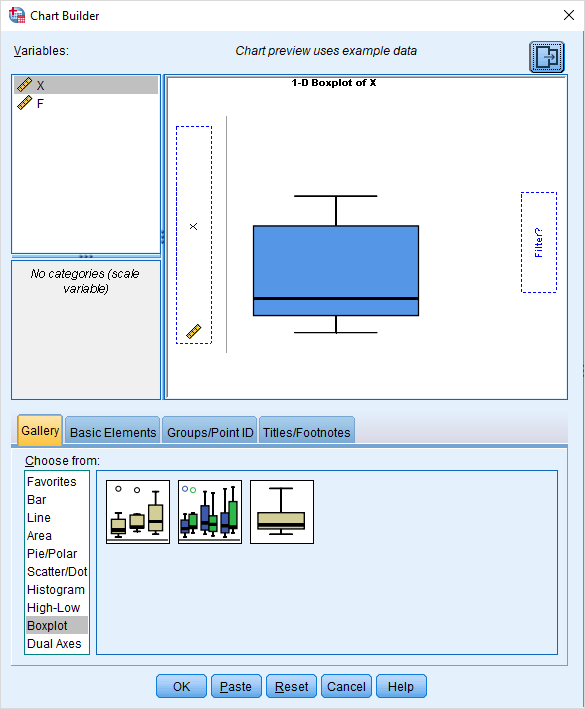
- از برگه Gallery و کادر Choose from گزینه Boxplot را انتخاب کرده و از بخش سمت راست آخرین نوع نمودار یعنی را انتخاب کنید. نمونه این پنجره گفتگو در تصویر ۸ قرار گرفته است.
- در کادر Variables،متغیر X را در کادر بالایی یا پیشنمایش نمودار (Chart Preview) در قسمت X-axis قرار دهید.
- دکمه OK را بزنید تا نمودار در پنجره Output ظاهر شود.
نتیجه اجرای این عملیات برای مجموعه داده جدول ۱ در تصویر 5 قرار گرفت است. همانطور که مشاهده میکنید، در این خروجی، با علامتهای دایره و ستاره، مشاهدات یا نقاط پرت مشخص شدهاند. فقط توجه داشته باشید که شمارههای قرار گرفته روی هر یک از نقاط، شمارهای است که در پنجره ویرایشگر داده مشخص شده است.
شناسایی نقطه پرت برای رابطه بین دو متغیر
شاید براساس دو متغیر بخواهیم یک نقطه پرت را شناسایی کنیم. البته در اینجا فرض بر این است که این دو متغیر بر یکدیگر تاثیرگذار هستند. معمولا برای محاسبه شدت رابطه بین دو متغیر از ضریب همبستگی آمار (Correlation) استفاده میشود. هر چه مقادیر این دو متغیر از یکدیگر بیشتر تاثیر بگیرند، ضریب همبستگی، به ۱ یا ۱- نزدیکتر است. ولی ممکن است بزرگی یا کوچکی این ضریب، به علت وجود نقطه پرت باشد.
بنابراین بهتر است قبل از تصمیم در مورد نحوه ارتباط بین دو متغیر، نمودار پراکندگی (Scatter plot) این دو متغیر را نسبت به یکدیگر ترسیم کنیم. برای مثال ممکن است فرض کنید در یک نمودار پراکندگی، نقطهای وجود دارد که با بقیه نقاط هم راستا نیست. وجود چنین نقطهای میتوان ضریب همبستگی را به شدت کاهش دهد و بیانگر عدم رابطه خطی بین دو متغیر باشد در حالیکه با حذف آن چنین رابطهای به خوبی دیده میشود.
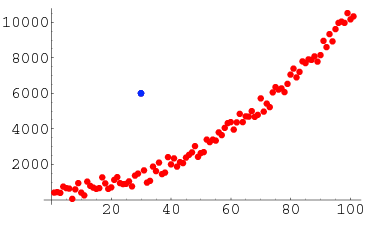
در تصویر ۹، که یک نمودار پراکندگی برای دو متغیر را ترسیم کردهایم، چنین وضعیتی به خوبی دیده میشود. وجود نقطه آبی رنگ باعث کاهش ضریب همبستگی شده ولی با حذف آن ضریب همبستگی افزایش خواهد یافت. در عین حال، وجود رابطه خطی بین دو متغیر به وضوح در این تصویر دیده میشود.
مثال ۳: مجموعه دادههای زیر را در نظر بگیرید. میخواهیم به کمک یک نمودار پراکندگی، مشاهده پرت را در SPSS مشخص کنیم.
جدول ۲: دادههای مرتبط با یکدیگر
| ردیف | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 1 | 5 | 8 | 10 | 5 | 6 | 3 | 9 | 10 | 15 |
| Y | 3 | 6 | 10 | 12 | 26 | 7 | 5 | 12 | 11 | 16 |
حال این اطلاعات را در مجموعه دادههای SPSS وارد میکنیم. تصویر زیر چنین مجموعه دادهای را در SPSS نشان میدهد.
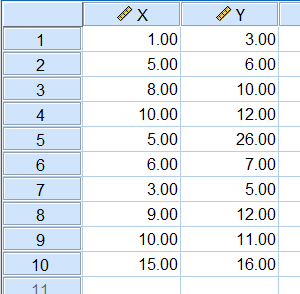
برای ترسیم نمودار پراکندگی بین این دو متغیر در SPSS، از مراحل زیر کمک میگیریم و نمودار Scatter Plot را برایشان ترسیم میکنیم. برای شناسایی داده پرت و انجام این کار مراحل زیر را مطابق با تصویر ۱۱، طی میکنیم.
- مقیاس (Measure) متغیرهای X و Y را از نوع Scale انتخاب کنید.
- از فهرست Graph گزینه Chart Builder را انتخاب کنید. سپس دکمه OK را بزنید.
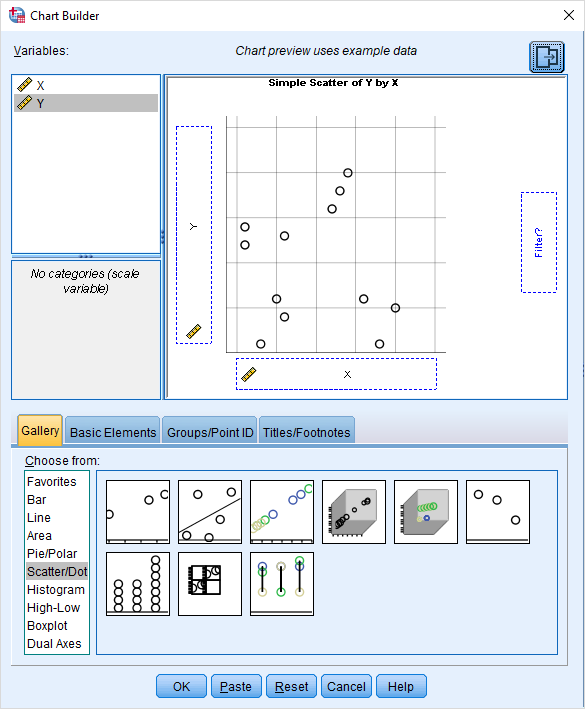
- از برگه Gallery و کادر Choose from گزینه Scatter/Dot را انتخاب کرده و از بخش سمت راست اولین نوع نمودار یعنی Simple Scatter را انتخاب کنید. نمونه این پنجره گفتگو در تصویر ۱۱، قرار گرفته است.
- از داخل کادر Variables، متغیر X را به کادر مربوط به محور افقی بکشید. متغیر Y را هم در کادر محور عمودی قرار دهید.
- دکمه OK را بزنید تا نمودار در پنجره Output ظاهر شود.
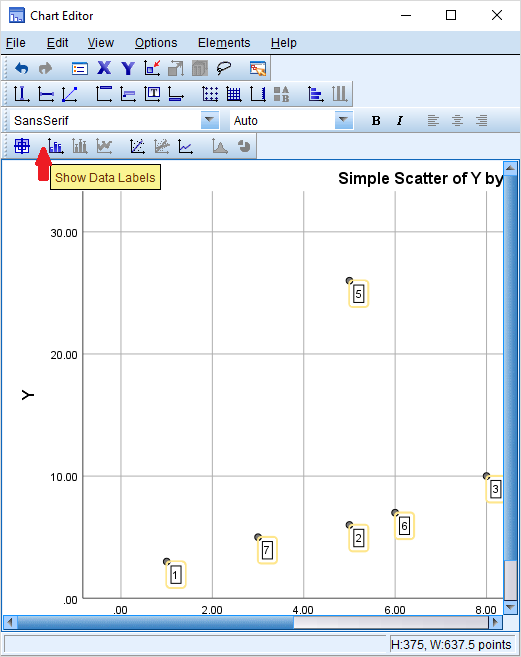
نتیجه ترسیم این نمودار در تصویر ۱۲ دیده میشود. نقطه قرمز رنگ در این نمودار، یک مشاهده پرت تلقی میشود. معمولا چنین نقاطی باید برای تجزیه و تحلیل کلی کنار گذاشته شده و به طور مجزا مورد بررسی قرار گیرند.
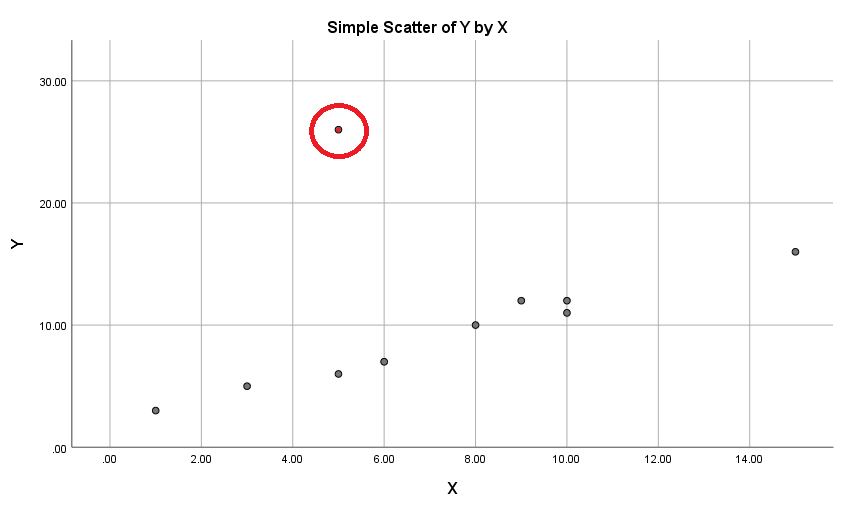
برای آنکه مشخص کنیم، این نقطه مربوط به کدام مشاهده است، روی نمودار در پنجره Output دوبار کلیک کنید تا به محیط ویرایشگر نمودار (Chart Editor) وارد شوید. به انتخاب دستور Show Data Labels از فهرست Elements، میتوانید شماره مشاهده مورد نظر را در نمودار ظاهر کنید. برای مثال ۳، مشاهده شماره ۵ به عنوان نقطه پرت معرفی شده است.
خلاصه و جمعبندی
همانطور که خواندید، در این نوشتار با استفاده از چند تکنیک آمار مبتنی بر شاخصهای آماری و البته رسم نمودارها، روشهای شناسایی داده پرت (Outlier) را در SPSS فرا گرفتیم. همانطور که دیدید، یک روش میتواند با تکیه بر توزیع و استفاده از خصوصیات «توزیع نرمال» (Normal Distribution) صورت گیرد و دیگری به روش تصویری و استفاده از روشهای ناپارامتری انجام میشود. به این ترتیب ترسیم یک نمودار فراوانی یا رسم نمودار جعبهای، محققین را در پیدا کردن دادههای پرت یاری میرساند. توجه داشته باشید که حضور داده پرت در تجزیه و تحلیلهای آماری ممکن است نتایج را منحرف کند در نتیجه پس از شناسایی داده پرت باید آنها را از مجموعه اطلاعاتی که برای پردازش لازم است، خارج کرد و محاسبات آماری و تحلیلها را انجام داد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای SPSS
- آموزش آماده سازی داده ها برای تحلیل آماری در SPSS
- مجموعه آموزشهای آمار و احتمال
- نمایش و رسم نمودار برای دادهها — معرفی و کاربردها
- رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی
- نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده
^^













سلام. ایا داده هایی که به صورت انلاین جمع اوری شده اند. داده های پرت دارند یا خیر؟
مطالب خوبی بود فقط برای شناسایی داده های دور افتاده روش آماری زیر هم می توان استفاده نمود:
آماره کیو تست(ًQ-test)تحت عنوان Dixon’s Q test که با محاسبه “کیو مورد انتظار” یا Q_exp و مقایسه با جدول توزیع آن آماره است یا “مقدار بحرانی کیو” یا Q_crit که در زیر آورده شده است:
Dixon Q Test for Outliers
Q_exp=0.857
Q_crit=0.97
Q_exp=0.857<Q_crit=0.97
پس داده پرت نیست و حفظ می شود.
Data number n = 10
پس داده پرت نیست و حفظ می شود.
و فرض صفر رد نمی شود.
یک سری عکس ها بود بین توضیحات که در قسمت نطر شما چیست برای سایت شما آنها را قبول نمی کند (فکر کنم عکس را در این قسمت قبول نمی کند)
چنانچه آدر س ایمیلتان را به ایمیل من بفرستید تحت عنوان Dixon Q Test for Outliers فایل و فیلم آموزشی را برایتان ایمیل می نمایم.
سلام و تشکر از راهنمای شما،
با اجازه، مطلبی نیز در مورد آزمون Dixon در مجله فرادرس منتشر خواهم کرد.
از این که همراه مجله فرادرس هستید، سپاسگزاریم.