رابطه هم ارزی و افراز مجموعه | به زبان ساده

یکی از ابزارهای مهم در نظریه مجموعه‌ها، تفکیک یا افراز مجموعه است. از طرفی رابطه هم ارزی نیز در بیان خصوصیات مجموعه‌ها، نقش مهمی دارد. در بیشتر مواقع با توجه به خصوصیات جالب در رابطه هم‌ارزی به دنبال پیدا کردن کلاس‌های هم‌ارزی در مجموعه‌ها هستیم. از طرف دیگر در حقیقت افراز، جداسازی و دسته‌بندی اعضای یک مجموعه در زیرمجموعه‌های جدا از هم و غیر تهی است به شرطی که اجتماع این زیرمجموعه‌ها، مجموعه اصلی را بسازد. در این نوشتار، نشان می‌دهیم که رابطه یا به شکل صحیح کلاس رابطه هم ارزی و افراز مجموعه معادل یکدیگر هستند. به دلیل اهمیت این موضوع، این مطلب از مجله فرادرس را به معرفی و آشنایی خوانندگان با رابطه هم ارزی و افراز مجموعه اختصاص داده‌ایم.

به منظور آگاهی از اصطلاحات مربوط به مجموعه و نظریه مجموعه‌ها، بهتر است نوشتارهای دیگر مجله فرادرس به عنوان‌های مجموعه ها در ریاضیات — مفاهیم پایه و رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده را مطالعه کنید. همچنین خواندن مطلب‌های اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده و عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده نیز خالی از لطف نیست.

رابطه هم ارزی و افراز مجموعه

قبل از هر چیز مفهوم رابطه هم‌ارزی (Equivalence Relation) را معرفی خواهیم کرد، سپس با معرفی افراز مجموعه (Set Partition)، به ارتباط بین رابطه هم ارزی و افراز مجموعه خواهیم پرداخت.

رابطه هم ارزی

یک رابطه از مجموعه $$A$$ به $$B$$ را در نظر بگیرید. به یاد دارید که یک رابطه، زیرمجموعه‌ای از ضرب دکارتی دو مجموعه است. اگر رابطه $$R$$ دارای خواص زیر باشد، آن را یک رابطه هم‌ارزی (Equivalence) می‌نامند.

• رابطه $$R$$ یک رابطه بازتابی یا انعکاسی (Reflective) باشد. به این معنی که هر عضوی از مجموعه با خودش در ارتباط باشد. به بیان دیگر برای هر عضو از مجموعه $$A$$ مثل $$x$$ داشته باشیم، $$(x,x) \in R$$
• رابطه $$R$$ یک رابطه تقارنی (Symmetric) باشد. یعنی اگر ترتیب قرارگیری مقادیر در رابطه تاثیری نداشته باشد. به بیان دیگر اگر زوج $$(x,y) $$ در $$R$$ باشند، آنگاه $$(y,x)$$ هم در رابطه هستند.
• رابطه $$R$$ یک رابطه «ترایا» یا «تراگذری» (Transitive) باشد. به این معنی که با داشتن گزاره‌های $$(x,y) \in R , (y, z) \in R$$ بتوان نتیجه گرفت که $$(x,z) \in R$$.

رابطه $$R$$ با خواص گفته شده را یک رابطه هم‌ارزی، و تمامی مجموعه‌هایی که با یک عضو مثلا $$x$$ در یک رابطه هم‌ارزی هستند را کلاس هم‌ارزی $$x$$ می‌نامند.

تعریف افراز مجموعه

یک افراز از مجموعه $$X$$ را به عنوان مجموعه‌ای از زیرمجموعه‌های غیرتهی از $$X$$ در نظر می‌گیرند که هر عضو از $$X$$ دقیقا فقط در یک زیرمجموعه حضور داشته باشد. به این ترتیب اجتماع زیرمجموعه‌های مجزای این افراز، مجموعه اصلی را می‌سازد.

همچنین می‌توان افراز را به صورت یک خانواده از مجموعه‌های $$P$$ در نظر گرفت، اگر و فقط اگر شرایط زیر برایشان برقرار باشند.

• خانواده $$P$$ شامل مجموعه تهی نیست.

$$ \large \emptyset \notin P $$

• اجتماع مجموعه‌های $$P$$ برابر با $$X$$ است. به بیان دیگر $$P$$ مجموعه $$X$$ را پوشش (Covers) می‌دهد.

$$ \large \cup_{A \in P} A = X $$

• اشتراک هر دو مجموعه در $$P$$، تهی است. به این معنی که اعضای مجموعه $$P$$، دو به دو جدا از هم هستند.

$$ \large {\displaystyle (\forall A, B \in P)\ ;A \neq B \implies A \cap B = \emptyset } $$

مجموعه‌های درون $$P$$ را اجزا (Blocks) یا سلول‌های (Cells) افراز می‌نامند.

نکته: رتبه $$P$$ نیز برابر با $$|X|-|P|$$ است به شرطی که $$X$$، متناهی باشد.

در ادامه با چند مثال تعریف ارائه شده برای افراز بوسیله خانواده‌ای از مجموعه‌ها را روشن‌تر می‌کنیم، سپس به معادل بودن رابطه هم ارزی و افراز مجموعه خواهیم پرداخت.

مثال از افراز مجموعه‌ها

در این قسمت با توجه به هر یک از مجموعه‌های معرفی شده، خانواده افرازهایی آن‌ها را مشخص خواهیم کرد.

• مجموعه تهی دارای فقط یک افراز است که به آن $$\emptyset$$ گفته می‌شود. توجه دارید که $$\emptyset$$ یک افراز بوده و عضوی از مجموعه تهی نیست.
• برای هر مجموعه غیر تهی مثل $$X$$، یکی از افرازها به صورت $$P=\{X\}$$ است که به آن افراز بدیهی گفته می‌شود.
• برای هر مجموعه غیرتهی مثل $$X$$، مجموعه‌ای که از سلول تک عضوی‌ $$\{x\}$$ تشکیل شده باشد، یک افراز مجموعه است. که آن را به صورت $$\{\{x\}\}$$ نشان می‌دهند.
• هر زیرمجموعه مانند $$A$$ از $$U$$ به همراه متمم آن (یعنی $$A’ = U – A$$) یک افراز از $$U$$ می‌سازند.
• مجموعه $$\{1,2,3\}$$ دارای ۵ افراز مختلف است که در ادامه هر یک از آن‌ها را مشخص می‌کنیم.
  • افراز تک عضوی که به صورت $$\{\{1\},\{2\},\{3\}\}$$ نوشته شده و گاهی با نماد $$1|2|3$$ نیز مشخص می‌شود. اجزا یا سلول‌های این افراز، تک تک اعضای مجموعه اصلی هستند.
  • افراز بدیهی $$\{\{1,2,3\}\}$$ که به صورت $$123$$ نیز نمایش داده می‌شود یک افراز از مجموعه اصلی است. مشخص است که نماد به کار رفته نمایانگر افراز است، زیرا از  دو علامت $$\{\}$$ برای نمایش آن استفاده شده است و اجزا یا سلول‌های افراز مجموعه، فقط از یک مجموعه تشکیل یافته‌اند.
  • افراز $$\{\{1,2\},3\}$$ یا $$12|3$$
  •  افراز $$\{\{1,3\},2\}$$ یا $$13|2$$
  • افراز $$\{\{1\},\{2,3\}\}$$ یا $$1|23$$

واضح است که برای مجموعه $$\{1,2,3\}$$، مجموعه‌های زیر یک افراز محسوب نمی‌شوند.

• مجموعه $$\{\{ \},\{1,2,3\}\}$$ یک افراز نیست. زیرا باید هر یک از بخش‌های افراز، غیرتهی باشند. در حقیقت، خانواده‌ای که شامل مجموعه تهی باشد، یک افراز برای هیچ مجموعه محسوب نخواهد شد.
• $$\{\{1,2\},\{2,3\}\}$$ نیز یک افراز نخواهد بود زیرا عضو $$2$$ در هر دو سلول یا جزء افراز، مشترک است. در نتیجه اجزای افراز دارای اشتراک بوده و دو به دو جدا از هم نیستند.
• $$\{\{1\},\{2\}\}$$ تشکیل یک افراز را نمی‌دهد زیرا اجتماع اجزای افراز، مجموعه اصلی را نمی‌سازد.

رابطه هم ارزی و افراز مجموعه

در این بخش به کمک مثال‌هایی، یکسان بودن رابطه هم ارزی و افراز مجموعه را مورد بررسی قرار می‌دهیم. مجموعه‌ای از کلاس‌های هم ارزی یک مجموعه مانند $$X$$ تحت یک رابطه هم‌ارزی، یک افراز از $$X$$ است. درست برعکس، از هر افراز $$P$$ از $$X$$، می‌توان یک رابطه هم ارزی روی $$X$$ به صورت $$x\sim y$$ تعریف کرد، بطوری که $$x,y$$ اجزای افراز $$P$$ باشند. به این ترتیب نماد رابطه هم‌ارزی و افراز معادل یکدیگر هستند.

«اصل موضوع انتخاب» (Axiom of Choice) تضمین می‌کند که برای هر افراز مجموعه $$X$$، زیرمجموعه‌ای از $$X$$ وجود دارد که دقیقا یکی از عناصر آن در هر یک از افرازها وجود دارد. این حقیقت، رابطه هم‌ارزی و افراز مجموعه را مشخص می‌کند. به این ترتیب با داشتن هر رابطه هم‌ارزی، افراز و با دانستن افراز، یک رابطه هم‌ارزی روی یک مجموعه بوجود می‌آید.

مثال: برای روشن‌تر شدن موضوع به مثال مربوط به مجموعه $$\{1,2,3\}$$ می‌پردازیم.

• کلاس هم‌ارزی $$\{1\}$$ را به صورت $$\{\{1\},\{2\},\{3\}\}$$ در نظر بگیرد. واضح است که این کلاس یک افراز برای مجموعه اصلی است.
• کلاس هم‌ارزی $$\{1,2\}$$ به صورت $$\{\{1,2\},\{3\}\}$$ نیز یک افراز برای مجموعه اصلی است.
• کلاس هم‌ارزی $$\{1,2,3\}$$ که به شکل $$\{\{1,2,3\}\}$$ نوشته می‌شود نیز یک افراز برای مجموعه $$\{1,2,3\}$$‌ است.

به این ترتیب مشخص است که براساس هر کلاس هم‌ارزی می‌توان یک افراز نوشت و هر افراز را مرتبط با یک کلاس هم‌ارزی در نظر گرفت.

پس هر رابطه هم‌ارزی (Equivalence Relation) یا به شکل صحیح، یک کلاس هم‌ارزی روی یک مجموعه، می‌تواند آن را تفکیک یا افراز کند. همچنین هر افرازی نیز یک رابطه هم‌ارزی می‌سازد. به تصویر 1، توجه کنید. همانطور که مشخص است، تمامی زیر مجموعه‌های ممکن برای پنج نقطه توسط خطوط و اشکال رنگی، مشخص شده است. همانطور که می‌بینید ۵۲ گونه تقسیم‌بندی یا افراز برای این پنج نقطه ترسیم شده است. از طرفی هر یک از این افرازها نیز یک رابطه هم ارزی را بیان می‌کنند. پس در اینجا هم رابطه هم ارزی و افراز مجموعه یکسان خواهند بود.

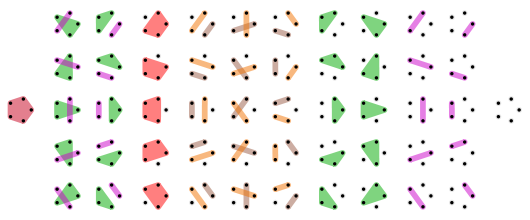
هر کدام از اشکال، یک افراز را نشان می‌دهد. در اولین شکل از سمت راست، تک تک نقطه‌ها نمایش داده شده‌اند که نشانگر یک افراز خواهد بود. همچنین در بخش دوم (ستون‌‌های دوم و سوم از سمت راست)، افرازهایی را مشاهده می‌کنید که دو عضو از اعضای مجموعه با یکدیگر در یک گروه قرار گرفته‌اند.

در مثلث‌های سبز رنگ نیز شاهد افرازهایی هستیم که یکی از زیرمجموعه‌ها، سه عضوی است. همینطور در انتها نیز خود مجموعه به عنوان یک زیر مجموعه از خودش، مشخص شده. واضح است که تک تک نقاط نیز می‌توانند زیرمجموعه‌هایی از مجموعه اصلی باشند.

نکته: هر کدام از شکل‌ها مربوط به تصویر ۱، یک افراز و یک کلاس هم‌ارزی تلقی می‌شوند و مشخص است ۵۲ افراز مختلف از این ۵ عضوی ایجاد شده است. نقطه‌های سیاه رنگ اعضای مجموعه اصلی را نشان می‌دهند. اشکال و رنگ‌هایی که نقطه‌های سیاه رنگ را در بر گرفته‌اند، اجتماع اعضای و یک سلول از افراز را نشان می‌دهند. باقی نقطه‌ها نیز به صورت تک به تک، اجزای افراز محسوب می‌شوند.

افراز نامتقاطع

یک افراز از مجموعه $$N = \{1,2,\ldots.n\}$$  با رابطه هم ارزی با نماد $$\sim$$ را در نظر بگیرید. این افراز را «نامتقاطع» (Noncrossing Partition) گویند اگر شرط زیر برایش برقرار باشد.

• چهار عنصر $$a,b,c,d$$ از $$N$$ را در نظر بگیرید که یک رابطه ترتیب اکید $$a<b<c<d$$ بینشان برقرار است. اگر $$a \sim b$$ و $$ b \sim d$$ آنگاه داشته باشیم $$a \sim b \sim c \sim d$$.

نامی که برای این افراز در نظر گرفته شده به این علت است که اگر عناصر مجموعه را به صورت یک نمودار چند وجهی با توجه به ترتیب یاد شده و خلاف جهت عقربه‌های ساعت ترسیم کنیم، خطوط مشخص کننده اجزای افراز، یکدیگر را قطع نمی‌کنند.

«مشبکه افرازهای نامتقاطع» (Lattice of noncrossing partitions) از این جهت اهمیت پیدا کرده است که در نظریه احتمال آزاد (Free Probability) نقش مهمی دارد.

به تصویر 2 توجه کنید. تمامی افرازهایی که به صورت متقاطع هستند براساس تصویر 1، جدا شده و در سمت راست این تصویر نمایش داده شده‌اند. با مقایسه تصویر سمت راست و سمت چپ این تصویر، تفاوت افرازهای نامتقاطع و متقاطع را خواهید دید. توجه دارید که برای تشکیل افرازهای نامتقاطع، احتیاج به یک رابطه ترتیبی اکید (یا حداقل ترتیب جزئی) داریم.

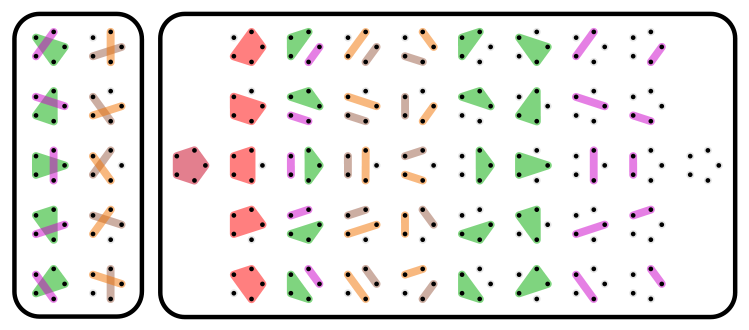
ظریف‌تر کردن افراز مجموعه

افراز $$a$$ از مجموعه $$X$$ را ظریف‌تر از افراز $$p$$ برای $$X$$ گویند، اگر هر عنصر از $$a$$ یک زیر مجموعه از بعضی از عناصر $$p$$ باشد. در این حالت می‌گوییم، $$a$$ ظریفتر از $$p$$‌ است، یا $$p$$ را درشت‌تر از $$a$$ می‌نامیم. به این ترتیب افراز $$a$$ پراکنده‌تر از $$p$$ به نظر می‌رسد. این امر را به صورت $$a \leq p$$ نشان می‌دهیم. مشخص است که چنین امری، نشانگر یکسانی رابطه هم ارزی و افراز مجموعه است.

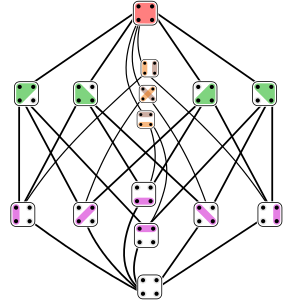
در تصویر 3، افرازهای یک مجموعه چهار عضوی دیده می‌شود. در ابتدای تصویر، درشت‌ترین افراز  که از همان افراز بدیهی است قرار گرفته است. هر چه تعداد سلول‌های افرازها بیشتر شود، افراز ظریف‌تر شده و در انتهای تصویر، افراز تشکیل شده از مجموعه‌های تک عضوی قرار می‌گیرد که از همه افرازهای دیگر ظریف‌تر است.

با توجه به «رابطه ظریفتر از» (Finer than Relation)، می‌توان یک «رابطه ترتیب جزئی» (Partial Order Relation) بین افرازهای مجموعه $$X$$ ایجاد کرد. در اینجا چنین رابطه‌ای را به صورت $$\leq $$ نشان می‌دهیم. هر مجموعه از  عناصر افراز دارای «کمترین کران بالا» (Sup) و «بزرگترین کران پایین» (inf) است. در نتیجه افرازها یک «مشبکه» (Lattice) ایجاد می‌کند که آن را می‌توان به صورت یک «مشبکه هندسی» (Geometric Lattice) به مانند «نمودار هسه» (Hasse Diagram) که در تصویر 3 دیده می‌شود، نمایش داد.

شمارش تعداد افرازها

برای یک مجموعه $$n$$ عضوی، تعداد افرازهای ممکن برابر با عدد بل (Bell numbers) یا $$B_n$$ است. این اعداد توسط ریاضیدان انگلیسی «اریک بل: (Eric Temple Bell) معرفی و به کار گرفته شد. اندیس $$n$$  در اعداد بل $$B_n$$، یک عدد صحیح مثبت است. به این ترتیب اعداد بل برای $$n=0,1,2,3,$$ به صورت زیر است.

$$ \large ‌B_0 = 1 , B_1 = 1 , B_2 = 2 , B_3 = 5 , … $$

اعداد بل در رابطه برگشتی زیر صدق می‌کنند.

$$ \large B_{ n + 1 } = \sum _{ k = 0 }^{n}{ n \choose k }B_{k} $$

توجه دارید که در اینجا منظور از $${ n \choose k}$$ ترکیب (Combination) تعداد $$k$$ شیئ از $$n$$ شیئ است. «تابع مولد نمایی» (Exponential Generating Function) آن نیز به فرم زیر است.

$$ \large\sum _{ n = 0}^{ \infty }{ \frac { B_{n}}{n!}}z^{n} = e^{ e^{z} – 1 }$$

برای نمایش اعداد بل، از مثلث بل نیز می‌توان کمک گرفت. در چنین مثلثی، آخرین عنصر سطر در اولین عنصر سطر بعدی قرار گرفته و اعداد دیگر مربوط به هر ردیف، بوسیله حاصل جمع عدد سمت چپ و مقدار سمت چپ ردیف قبلی حاصل می‌شود. در تصویر 4، شیوه تشکیل این مثلث و اعداد بل نمایش داده می‌شود. این مثلث از هر دو طرف تکرار شده و مثلث کامل می‌شود.

به این ترتیب ستون اول در این مثلث، نشانگر تعداد افرازهای یک مجموعه با صفر (تهی)، یک و … عضوی است. در تصویر 5، تعداد افرازهای ممکن برای مجموعه‌ها تا ۱۰ عضو در اکسل محاسبه و مشخص شده است.

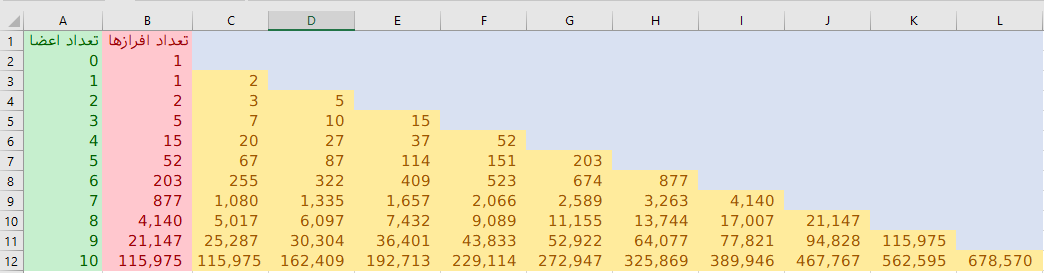
همانطور که در تصویر 5، دیده می‌شود، تعداد افرازهای یک مجموعه پنج عضوی برابر با ۵۲ است که تصویر 1، نیز آن را تایید می‌کند. اعضای کلاس هم‌ارزی یا تعداد رابطه هم ارزی و افراز مجموعه نیز در این حالت یکسان خواهد بود.

تعداد افرازهای یک مجموعه $$n$$‌ عضوی به $$k$$ سلول یا بخش مجزا همان «عدد استرلینگ از نوع دوم» (Stirling number of the second kind) است که با نماد $$S(n,k)$$ یا $$ \{ { n  \atop k} \}$$ نشان داده شده و به شکل زیر محاسبه می‌شود.

$$ \large { \displaystyle S(n , k) = \left\{{n \atop k} \right\} = { \frac {1}{k!}} \sum _{ i = 0}^{k}(-1)^{i}{ \binom {k}{i}}( k- i )^{n}}$$

همچنین تعداد افرازهای نامتقاطع برای مجموعه $$n$$ عضوی برابر با «عدد کاتالان» (Catalan Number) با نماد $$C_n$$ است که به شکل زیر محاسبه می‌شود.

.$$ \large { \displaystyle C_{n} = {1 \over n + 1}{ 2n \choose n }} $$

خلاصه و جمع‌بندی

در این نوشتار با رابطه هم ارزی و افراز مجموعه، نحوه تشکیل افرازها براساس کلاس هم‌ارزی و همچنین تعداد افرازهای ممکن برای یک مجموعه آشنا شدید. به این ترتیب هر افراز می‌تواند یک رابطه هم‌ارزی ایجاد کرده و برعکس می‌توان یک رابطه هم‌ارزی را به صورت افراز نمایش داد. مثال‌هایی نیز برای نحوه تشکیل و همچنین قوانین شمارش افرازهای ممکن یک مجموعه در این نوشتار از مجله فرارس بیان شد. همچنین مشخص شد که رابطه هم ارزی و افراز مجموعه معادل هستند. هر چند افراز مفهوم ساده و قابل درکی برای مجموعه‌ها است ولی نقش آن در آنالیز ریاضی و بخصوص ریاضیات مدرن و نظریه مجموعه‌ها، بسیار اهمیت دارد. بسیاری از قضیه‌های پیچیده در نظریه اندازه نیز به کمک افراز یا تفکیک، قابل حل شدن هستند و قضیه‌های جدید توسعه داده می‌شوند. به همین دلیل در این نوشتار سعی شده مفهوم آن یادآوری شود تا کسانی که به ریاضیات مدرن علاقمند هستند، با پایه‌های نظریه مجموعه‌ها آشنا شوند.