درخت در ساختمان داده چیست؟ — به زبان ساده + انواع

ساختمان داده درخت به عنوان مجموعه‌ای از اشیاء یا موجودیت‌هایی به نام گره‌ (Node) تعریف می‌شود که به صورت سلسله مراتبی (به وسیله یال) به یکدیگر مرتبط شده‌اند. درخت ساختمان داده‌ای غیرخطی است، زیرا داده‌ها را نه به صورت متوالی، بلکه به صورت سلسله‌مراتبی ذخیره می‌کند. در ساختمان داده درخت، اولین گره به عنوان گره ریشه شناخته می‌شود. درخت از گره ریشه شروع می‌شود و توسعه می‌یابد. هر گره حاوی داده ‌و همچنین حاوی ارجاعاتی به گره‌های فرزند است. یک گره ریشه هرگز نمی‌تواند گره والد داشته باشد.

ضرورت وجود درخت در ساختمان داده

سایر ساختمان‌ داده‌ ها مانند آرایه‌ها، لیست پیوندی، پشته‌ها و صف‌ها، ساختمان داده‌‌های خطی هستند و همه این ساختارها، داده‌ها را به ترتیب و به صورت متوالی ذخیره می‌کنند و در نتیجه پیچیدگی زمانی با افزایش اندازه داده‌ها برای انجام عملیاتی مانند درج و حذف به صورت خطی افزایش می‌یابد که در دنیای محاسبات امروزی قابل قبول نیست.

فیلم آموزش رایگان ساختمان داده ها – سریع و آسان در ۱۲۰ دقیقه در فرادرس

کلیک کنید

ساختار غیرخطی درختان، فرآیندهای ذخیره‌سازی، دسترسی به داده‌ها و دستکاری داده‌ها را با استفاده از روش‌های پیمایش و کنترل افزایش می‌دهد.

اصطلاحات رایج درخت در ساختمان داده

درخت یک ساختمان داده سلسله مراتبی است که به عنوان مجموعه‌ای از گره‌ها تعریف می‌شود. در یک درخت، گره‌ها مقادیر را نشان می‌دهند و توسط یال‌ها به هم متصل می‌شوند. در تصویر زیر برخی از اصطلاحات اصلی مورد استفاده در درخت ساختمان داده به صورت بصری نشان داده شده است.

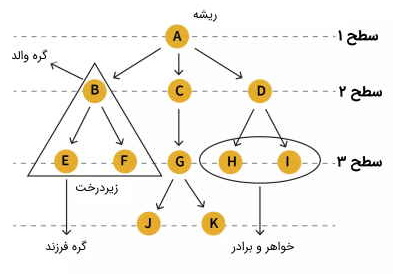
در ادامه، هر یک از این اصطلاحات و اجزای درخت به طور خلاصه شرح داده شده‌اند و در انتها نیز پیوند دسترسی به جدول اصطلاحات رایج درخت در ساختمان داده آمده است.

• ریشه (Root): در ساختار داده درختی، گره ریشه اولین گره یا گره والد است. گره ریشه گرهی است که کل درخت از آن سرچشمه می‌گیرد. گره ریشه والد ندارد و فقط دارای گره‌های فرزند است. در تصویر بالا، گره A ریشه درخت محسوب می‌شود.
• گره والد (Parent Node): گره‌ای که بلافاصله ماقبل یک گره مفروض قرار دارد، گره والد آن گره مفروض نامیده می‌شود. در تصویر بالا، B والد E و F است.
• گره فرزند (Childe Node): همه گره‌هایی که بلافاصله بعد از یک گره مفروض قرار دارند و وارث آن به حساب می‌آیند، فرزندان آن گره مفروض هستند. در تصویر بالا، F و E فرزندان B محسوب می‌شوند.
• برگ (Leaf): گره‌ای که هیچ فرزندی ندارد، برگ نامیده می‌شود. معمولاً گره‌های مرزی یک درخت یا آخرین گره‌های درخت، برگ‌های درخت نامیده می‌شوند. در تصویر بالا، E ، F ، J ، K ، H ، I گره‌های برگ هستند.
• یال (Edge): یال ارتباطی است بین دو گره و به وسیله خطی اتصال‌دهنده بین آن دو گره نشان داده می‌شود. در درختی با n گره، تعداد یال‌ها برابر با n-1 خواهد بود. در تصویر بالا، خط اتصال بین A و B یا A و C یا B وF یا هر گره دیگری که به یکدیگر متصل می‌شوند را یال می‌نامیم.
• همزاد (Siblings): همزاد در زندگی واقعی به معنای افرادی با والدین یکسان است، به طور مشابه در مورد درختان، گره‌هایی با والدین مشترک، همزاد در نظر گرفته می‌شوند. در تصویر بالا، H و I همزاد هستند.
• مسیر (Path): مسیر، تعدادی یال متوالی از گره مبدا تا گره مقصد است. در تصویر بالا، A ، C ، G ، K مسیری از گره A به K به حساب می‌آید.
• ارتفاع گره (Height of Node): ارتفاع یک گره نشان دهنده تعداد یال‌های طولانی‌ترین مسیر بین آن گره و یک برگ است. در تصویر بالا، A ، C ، G و K ارتفاع را تشکیل می‌دهند. ارتفاع A برابر با تعداد یال‌های بین A و K برابر با ۳ است. به طور مشابه ارتفاع G برابر با یک است زیرا فقط یک یال تا گره برگ بعدی دارد.
• سطح گره (Levels of Node): سطح یک گره نشان دهنده نسل آن گره است. گره ریشه در سطح صفر قرار دارد و گره فرزند بعدی آن در سطح یک و نوه آن در سطح ۲ است. در تصویر بالا، سطح H ، I و J برابر با ۳ و سطح D ، E ، F و G برابر با ۲ است.
• درجه گره (Degree of Node): درجه یک گره مفروض به تعداد گره‌های فرزند آن گره مفروض گفته می‌شود. در تصویر بالا، درجه D برابر با ۲ و درجه C برابر با ۳ است.
• بازدید (Visiting): هنگامی که مطابق با برنامه، پیمایش به یک گره خاص انجام می‌شود، بررسی یا دسترسی به مقدار گره جاری، بازدید نامیده می‌شود.
• گره داخلی (Internal Node): گره‌ای که حداقل یک فرزند داشته باشد، به عنوان گره داخلی شناخته می‌شود. در تصویر بالا، تمام گره‌ها به جز E ، F ، J ، K ، H ، I داخلی هستند.
• پیمایش (Traversing): پیمایش، فرآیند بازدید از یک گره با ترتیب و نظمی خاص است. سه نوع پیمایش وجود دارد که شامل پیمایش‌های به‌ترتیب، پیش‌ترتیب و پس‌ترتیب هستند.
• گره اجدادی (Ancestor Node): اجداد یک گره، همه گره‌های پیشین از ریشه تا آن گره هستند. یعنی والدین در نسل‌های مختلف مربوط به یک گره خاص، اجداد آن گره هستند. در تصویر بالا، A ، C و G اجداد گره‌های K و J هستند.
• نسل (Descendant): گره‌ای که بلافاصله بعد از یک گره مفروض قرار می‌گیرد از نسل آن گره مفروض نامیده می‌شود. در تصویر بالا، K از نسل G است.
• زیردرخت (Sub Tree): نوادگان یک گره، نشان دهنده زیردرخت هستند. درخت به عنوان یک ساختمان داده بازگشتی می‌تواند شامل بسیاری از زیردرخت‌ها در داخل خود باشد. در تصویر بالا، گره‌های B ، E ، F نشان دهنده یک زیردرخت هستند.

برای مشاهده جدول اصطلاحات فنی درخت در ساختمان داده + اینجا کلیک کنید.

فیلم آموزش ساختمان داده ها – جامع و با نکات مهم در فرادرس

کلیک کنید

درخت کامل در ساختمان داده

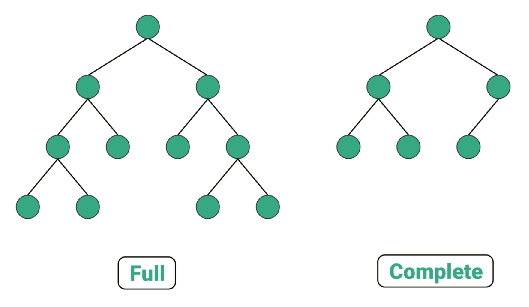
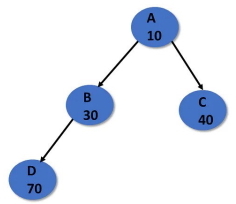
درخت کامل دودویی درختی است که به استثناء سطح آخر کاملاً پًر شده است که در سطح آخد تا جای امکان از سمت چپ به راست پُر می‌شود. یک درخت کامل دودویی با ارتفاع $$h$$ بین $$2^h$$ و $$2^{h+1}$$ گره دارد. در درخت دودویی کامل یک گره می‌تواند تنها یک فرزند داشته باشد.

در یک «درخت دودویی پُر شده» (Full Binary Tree) یک گره نمی‌تواند تنها یک فرزند داشته باشد. در درخت دودویی کامل، گره باید از چپ به راست پُر شود. در درخت Full هیچ ترتیبی برای پر کردن گره‌ها وجود ندارد.

ویژگی‌های ساختمان داده درخت

در این بخش به ویژگی‌های یا خاصیت‌های مهم درخت در ساختمان داده پرداخته شده است. از جمله این خاصیت‌های می‌توان به بازگشتی بودن، امکان محاسبه تعداد یال از روی تعداد گره‌ها و سایر موارد اشاره کرد.

بازگشتی بودن ساختار داده درخت

متد بازگشتی متدی است که خود را فراخوانی می‌کند. به طور مشابه، یک ساختمان داده بازگشتی، ساختاری است که خود را شامل می‌شود. یک درخت را می‌توان به عنوان یک ساختمان داده بازگشتی در نظر گرفت، زیرا هر گره به عنوان یک گره ریشه برای زیردرخت‌های دیگر به حساب می‌آید. برای درک بهتر این موضوع، در ادامه مثالی ارائه شده است.

مثالی برای درک بهتر خاصیت بازگشتی بودن درخت در ساختمان داده

در شکل زیر، درخت شماره ۱ را با گره ریشه "A" ملاحظه می‌کنید. زیردرخت‌های موجود شامل درخت‌های ۲ و ۳ با ریشه‌های به ترتیب "C"و "D" به خودی خود درختان مستقلی محسوب می‌شوند. به این ترتیب یک درخت شامل چندین زیردرخت است، و بنابراین درخت یک ساختمان داده بازگشتی به حساب می‌آید چرا که ساختمان داده بازگشتی خود را شامل می‌شود.

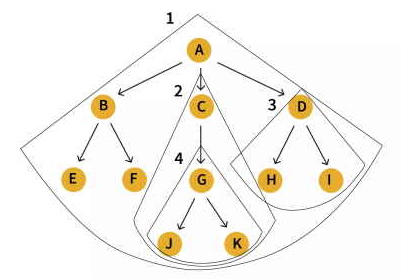
• نکته: حتی گره‌های برگ نیز به خودی خود یک درخت هستند، یعنی می‌توان یک گره برگ را به تنهایی به عنوان درختان بدون گره فرزند در نظر گرفت.

رابطه ثابت بین تعداد یال و گره در ساختمان داده درخت

اگر در یک درخت تعداد $$n$$ گره وجود داشته باشد، تعداد یال‌ها n-1 خواهد بود. یال خط جهت‌داری است که دو گره را به هم متصل می‌کند.

فیلم آموزش ساختمان داده ها و پیاده سازی در سی پلاس پلاس C++‎ در فرادرس

کلیک کنید

ویژگی عمق گره در ساختمان داده درخت

عمق گره x برابر با طول مسیر از ریشه تا گره x تعریف می‌شود. هر یک یال به اندازه یک واحد، عمق گره را افزایش می‌دهد. بنابراین عمق گره x را می‌توان برابر با تعداد گره‌ها از گره ریشه تا گره x نیز در نظر گرفت. عمق گره x برابر است با:

$$depth = L + 1$$ (تعداد سطوح از ریشه تا سطح L به اضافه ۱)

در رابطه فوق،‌ سطح L سطحی است که گره x در آن قرار دارد. باید توجه داشت که سطح اول با صفر شروع می‌شود.

ارتفاع گره درخت در ساختمان های داده

ارتفاع یک گره نشان دهنده تعداد یال‌های طولانی‌ترین مسیر بین آن گره و یک برگ است. در ادامه به موضوع پیاده‌سازی درخت در ساختمان داده پرداخته شده است؛ پیش از آن، ابتدا به معرفی مجموعه دوره‌های آموزش ساختمان داده و طراحی الگوریتم برای یادگیری بیشتر پرداخته شده است.

پیاده سازی ساختار داده درخت

در تصویر زیر نشان داده شده است که درخت در حافظه چگونه قرار می‌گیرد. بر این اساس، هر گره از سه فیلد تشکیل شده است. قسمت چپ گره شامل آدرس حافظه فرزند چپ، قسمت راست گره شامل آدرس حافظه فرزند سمت راست و قسمت مرکزی، حاوی داده ذخیره شده در این گره است.

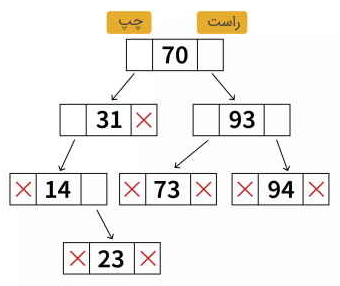
مطابق با بیان بالا، هر گره را می‌توان در برنامه نویسی به صورت یک کلاس تعریف کرد:

1Class Node {
2    public int value;
3    public Node left;
4    public Node right; 
5}

در قطعه کد بالا، left به گره‌ای (شیNode ) اشاره دارد که مقدار آن کمتر از مقدارNodeجاری است. به همین ترتیب،right به گره‌ای (شیNode ) اشاره دارد که مقدار آن بیشتر ازNode جاری است. در اینجا بحث مربوط به درخت دودویی می‌شود. درخت دودویی در بیشترین حالت، دارای دو فرزند است. یعنی یک گره دارای صفر، یک یا حداکثر ۲ فرزند است. یک «درخت عمومی‌» (Generic Tree) می‌تواند بیش از ۲ فرزند نیز داشته باشد.

معرفی فیلم های آموزش ساختمان داده و طراحی الگوریتم

مبحث درخت یکی از سرفصل‌های آموزش‌های ساختمان داده و طراحی الگوریتم است. ساختمان داده و طراحی الگوریتم از آموزش‌های پایه، مهم و پیش‌نیاز دیگر آموزش‌ها در علوم کامپیوتر به حساب می‌آید. فرادرس در قالب مجموعه‌ای جامع و کاربردی، دوره‌های آموزشی ساختمان داده و طراحی الگوریتم را منتشر کرده است. تصویر بالا تنها برخی از آموزش‌های ارئه شده در این مجموعه را نمایش می‌دهد.

‍

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

• برای شروع یادگیری ساختمان داده و طراحی الگوریتم و دسترسی به تمام دوره‌های این مجموعه + اینجا کلیک کنید.

کاربرد درخت در ساختمان داده

ساختمان داده درخت به صورت عملیاتی در دنیای واقعی کاربرد دارد و مورد استفاده قرار می‌گیرد. در ادامه به برخی از این کاربردها اشاره شده است.

پیمایش درخت

یکی از مهم‌ترین کاربردهای درخت، پیمایش در «مدل شی سند» (Document Object Model | DOM) است. «پیمایش» از طریق درخت برای دسترسی برنامه‌نویسان به گره‌های مرتبط، امکان‌پذیر می‌شود و به این ترتیب امکان دسترسی به تمام همزادهای یک گره مفروض ممکن می‌شود. ساختمان داده درخت به مسیری برای مفسر HTML تبدیل شده است و می‌تواند سراسر سند HTML را پیمایش کند.

جستجو با ساختمان داده درخت

از آنجایی که درخت ساختمان داده‌ای سلسله مراتبی به حساب می‌آید و هر گره به گره دیگری متصل است، از این رو دسترسی به یک گره داده خاص به راحتی و به صورت کارآمد امکان‌پذیر خواهد بود. درخت جستجوی دودویی را در نظر بگیرید که نسخه بهبودیافته‌ای از یک درخت به حساب می‌آید، زیرا هر گره حداکثر ۲ گره فرزند دارد. یعنی یک گره چپ و یک گره راست در این ساختمان داده وجود دارد. گره چپ داده‌ای را در خود جای می‌دهد که کمتر از داده گره جاری است و گره سمت راست، داده‌هایی بزرگ‌تر از داده‌های گره جاری دارد. بنابراین جستجوی یک داده خاص در درخت جستجوی دودویی آسان است.

با وجود اینکه درخت جستجوی دودویی امکان جستجوی بهینه را فراهم می‌کند، اما باید این مسئله را هم در نظر گرفت که نیاز به تلاش بیشتری برای ایجاد درخت جستجوی دودویی وجود دارد. پیچیدگی زمانی یا همان مرتبه اجرایی جستجوی یک عنصر در درخت جستجوی دودویی معادل O(H) است، که در آن H ارتفاع درخت است. O(H) نه تنها جستجو را کارآمد می‌کند، بلکه درج و حذف را در هر گره درخت امکان‌پذیر می‌کند. از این رو سازماندهی داده‌ها در یک درخت نیز با درج و حذف کارآمد در هر گره ممکن می‌شود.

فیلم آموزش ساختمان داده ها – جامع و با نکات مهم در فرادرس

کلیک کنید

تصمیم گیری به کمک ساختار درخت

درخت در ساختمان داده را می‌توان به عنوان ساختاری به کار گرفت که در آن هر گره تصمیمی را به تصویر می‌کشد که توسط کاربر اتخاذ شده است. هر گره دو انتخاب را در اختیار ما قرار می‌دهد و وقتی کاربر یکی را انتخاب می‌کند، یک قدم به سمت پایین درخت حرکت می‌کند. با رسیدن به یک برگ، به تصمیم نهایی می‌رسیم.

از این رو، تمام جریان‌ها در هر کاربردی را می‌توان در یک درخت به گونه‌ای تصویرسازی کرد که هر جریان و همه جریان‌ها تعریف شده‌اند و جریان‌ها در یک کاربرد بی‌نهایت نیستند (مگر آنکه دایره‌ای باشند).

برای مثال در نمودار زیر چند انتخاب نشان داده شده است که در آن کاربر باید در حین انتخاب فیلم در مورد آن‌ها تصمیم‌گیری کند. از این رو، جریان‌های مربوطه برای رسیدن به فیلمی که کاربر می‌خواهد ببیند بسیار محدود هستند.

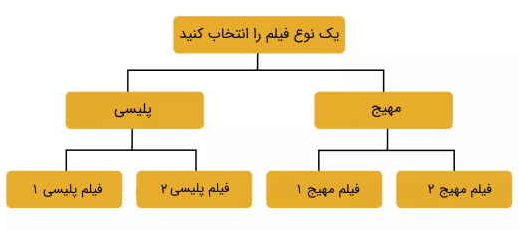
از دیدگاه مشتری یا کاربر، ممکن است این ساختار یکسان به نظر نرسد. اما از منظر برنامه یا کدهای برنامه، ساختار داده درخت مانندی وجود دارد که از ساختاری مشابه تصویر بالا پیروی می‌کند. بنابراین به واسطه ساختار داده درختی، الگوریتمی بدست می‌آید که می‌تواند به کاربر امکان دهد اپلیکیشن‌های پخش فیلم را به‌گونه‌ای جست و جو کنند که بتوانند بهترین فیلم پیشنهادی موجود را بیابند.

اما اگر اپلیکیشن مربوطه دارای قابلیت خودکار نمایش بهترین فیلم پیشنهادی به کاربر باشد، آیا امکان پیدا کردن فیلم جدیدی وجود دارد که کاربر تا کنون ندیده است و احتمال لذت بردن کاربر از آن فیلم هم بیشینه باشد؟ برای پاسخ به این پرسش، یکی دیگر از کاربردهای مهم ساختار درخت، یعنی یادگیری ماشین مطرح می‌شود که در ادامه به آن پرداخته شده است.

فیلم آموزش ساختمان داده ها با پایتون در فرادرس

کلیک کنید

کاربرد ساختمان داده درخت در یادگیری ماشین

برای اینکه ماشین به طور خودکار برای کاربر تصمیم بگیرد، ماشین به داده‌های تاریخی بسیار و روند داده‌های زیادی در مورد انتخاب دستی داده‌ها توسط کاربر نیاز دارد، به‌طوری که ماشین با انتخاب‌های گذشته کاربر سازگار می‌شود.

با فرض داشتن چنین داده‌هایی، دسترسی به ساختمان داده درخت و مجموعه داده‌های تاریخی به ماشین داده می‌شود تا آمار و مجموعه داده‌های خودش را داشته باشد و به این وسیله روندها و الگوهای موجود در داده‌ها را درک کند (در فضای این مثال، منظور تصمیم‌گیری در مورد انتخاب فیلم برای کاربر است) و به نوعی این امکان فراهم می‌شود تا ماشین برای هر گره داده‌هایی را تعیین کند.

با فرض اینکه برنامه‌ای وجود داشته باشد که الگوریتم را با استفاده از ساختمان داده درخت اجرا می‌کند تا بر اساس مجموعه داده‌های ارائه شده به نتیجه برسد (در این مورد، نتیجه بهترین فیلم ممکن است). در ابتدا، ساختمان داده با هر داده‌ای شروع می‌کند که برایش فراهم شده است. در ادامه برنامه از با استفاده از تک تک داده‌ها تکرار می‌شود، و بارها به نتایج اشتباه می‌رسد. اما زمانی که برنامه به تعداد قابل توجهی از تکرارها برسد، گرایش آن به نتیجه‌گیری اشتباه کاهش می‌یابد، زیرا اکنون آمار خاص خود را خواهد داشت (مثلاً اینکه کاربر چه دسته‌ای را بیشتر تماشا می‌کند، چه نوع فیلم‌هایی را معمولاً رد می‌کند، چه نوع فیلم‌هایی را ناتمام رها می‌کند و غیره).

بر اساس این روند داده‌ها و آمارها، ساختمان داده درختی به برنامه اجازه می‌دهد تا به نتیجه درست متمایل شود که در مثال ما، انتخاب بهترین فیلم برای کاربر است. همه چیز به داده‌های موجود در گره‌های درختان بستگی دارد. اگر برنامه روند داده‌ها و آمار مناسب را جمع آوری کند و اگر داده‌ها به درستی در گره‌های ساختمان داده درخت استفاده شوند و الگوریتم تصمیم‌گیری به درستی تشخیص دهد که فرزند مناسب بعدی چیست، آنگاه برنامه عمدتاً به نتیجه درست خواهد رسید.

• توجه: موارد بالا تنها برخی از توضیحاتی هستند که به ما امکان می‌دهند تا ساختمان داده درختی را با موقعیت‌های دنیای واقعی مرتبط کنیم و این فقط ایده‌ای سطح بالا است که چگونه ساختمان داده درخت را می‌توان در یادگیری ماشین یا تصمیم‌گیری یا سازمان‌دهی فایل‌ها در ماشین اعمال کرد.

فیلم آموزش درخت تصمیم در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

دیگر کاربردهای ساختار داده درخت

از جمله سایر کاربردهای ساختار درخت می‌توان به موارد زیر اشاره کرد.

• «درخت هرمی» (Heap Tree) نوعی درخت است که برای مرتب‌سازی هرمی استفاده می‌شود.
• «درخت پیشوندی» (Trie) نسخه اصلاح شده درخت مورد استفاده در مسیریابی مودم به اطلاعات روتر است.
• در برخی از سیستم‌های مدیریت بانک اطلاعاتی از B-tree استفاده می‌شود.
• کامپایلرها از درخت‌های نحوی برای بررسی سینتکس برنامه استفاده می کنند.

انواع درخت در ساختمان داده چیست ؟

در شرح کاربردهای ساختمان داده درخت تلویحاً به برخی از انواع درخت در ساختمان داده اشاره شد. در این بخش سعی شده است هر یک از انواع ساختارهای درختی تا حد امکان به‌طور جامع معرفی شود. ابتدا در ادامه هر یک از انواع درخت در ساختمان داده تنها فهرست شده‌اند.

• درخت عمومی (Generic)
• درخت دودویی (Binary)
• درخت جستجوی دودویی (Binary Search)
• درخت AVL
• درخت سرخ-سیاه (Red–black)
• درخت گسترده (Splay Tree)
• درخت تریپ (Treap)

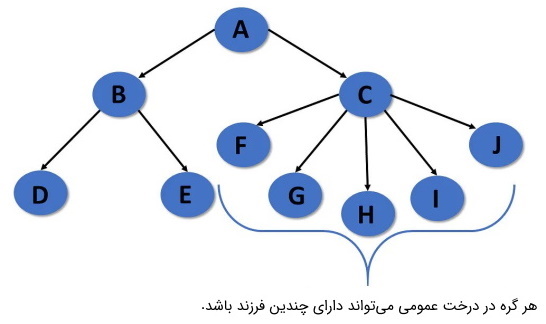
درخت عمومی در ساختمان داده

«درخت عمومی» (Generic Tree) یکی از انواع درخت در ساختمان داده است که در ساختار سلسله مراتبی آن محدودیتی برای تعداد گره‌ها وجود ندارد. هر گره دارای صفر تا n گره است. درخت عمومی با یک گره ریشه شروع می‌شود و فرزندان گره والد، یک زیردرخت عمومی‌ دیگر می‌سازند. از این رو، هر گره ریشه یک زیردرخت است، یعنی در یک درخت عمومی‌، تعداد n زیردرخت وجود دارد. همه زیردرخت‌ها در یک درخت عمومی‌ نامرتب قرار دارند.

ویژگی های درخت عمومی در ساختمان داده

خصوصیت‌های این نوع درخت در ادامه آمده است.

• درخت عمومی از تمام خصوصیات ساختمان داده درخت پیروی می کند.
• یک گره می‌تواند هر تعداد گره داشته باشد.

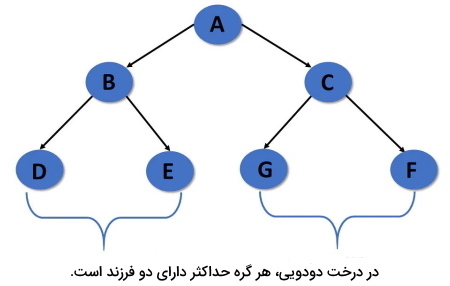
درخت دودویی در ساختمان داده

«درخت دودویی» (Binary) یکی از انواع درخت در ساختمان داده است که در آن هر گره می‌تواند حداکثر ۲ فرزند (یعنی تعداد صفر، یک یا ۲ فرزند) داشته باشد. هیچ محدودیتی در مورد داده‌های فرزند چپ یا فرزند راست وجود ندارد.

ویژگی های درخت دودویی در ساختمان داده

این ویژگی‌ها در ادامه فهرست شده‌اند.

• این نوع درخت از تمام خصوصیات ساختمان داده درخت پیروی می‌کند.
• درخت دودویی می‌تواند حداکثر دو گره فرزند داشته باشند.
• این دو فرزند را فرزند چپ و فرزند راست می‌نامند.

درخت جستجوی دودویی در ساختمان داده

یکی دیگر از انواع درخت در ساختمان داده، درخت جستجوی دودویی است که بسط فشرده‌تری از درخت دودویی به حساب می‌آید. درخت جستجوی دودویی درست مانند درخت دودویی می‌تواند حداکثر ۲ فرزند داشته باشد. این نوع درخت می‌تواند n گره داشته باشد و همچنین هر گره را می‌توان به عنوان یک بخش داده تعریف کرد که داده‌ها را در فرزند سمت چپ و فرزند سمت راست نگه می‌دارد. فرزند سمت چپ ارجاع به گره حاوی داده‌هایی را انجام می‌دهد که کمتر از داده‌های گره جاری است و به طور مشابه فرزند سمت راست حاوی ارجاع به گره حاوی داده‌هایی است که دقیقاً بزرگتر از داده‌های گره جاری هستند.

ویژگی های درخت دودویی در ساختمان داده

خصوصیات درخت دودویی به شرح زیر است.

• درخت دودویی هم از تمام خصوصیات ساختمان داده درخت پیروی می‌کند.
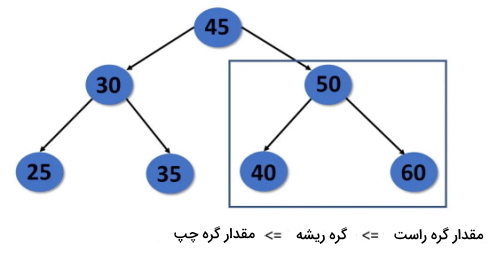
• درخت جستجوی دودویی دارای یک ویژگی منحصر به فرد است. این ویژگی بیان می‌کند که مقدار یک گره فرزند سمت چپ درخت باید کمتر یا مساوی با مقدار گره والد درخت باشد و مقدار گره فرزند سمت راست باید بزرگتر یا مساوی با مقدار والد باشد.

درخت AVL در ساختمان داده

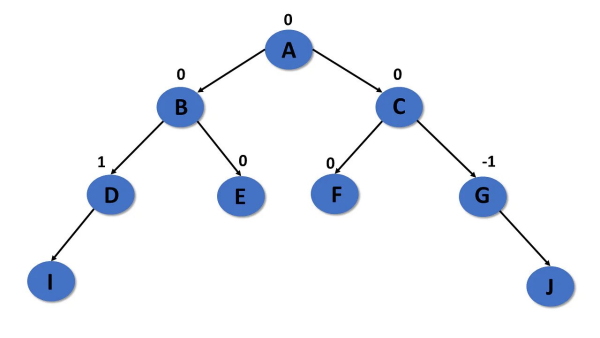
درخت AVL از دیگر انواع درخت در ساختمان داده است. می‌توان آن را درخت دودویی و همچنین نوعی درخت جستجوی دودویی در نظر گرفت. این نوع درخت هم ویژگی‌های درخت دودویی و هم ویژگی‌های درخت جستجوی دودویی را دارد. این یک درخت خود متعادل‌ساز است، یعنی ارتفاع زیردرخت سمت چپ و زیردرخت راست را متعادل می‌کند.

این تعادل با چیزی به نام عامل متعادل‌کننده مشخص می‌شود. درختی به عنوان درخت AVL در نظر گرفته می‌شود که ویژگی‌های درخت جستجوی دودویی و عامل متعادل کننده را برآورده کند. تفاوت بین ارتفاع زیردرخت سمت چپ و زیر درخت سمت راست به عنوان ارتفاع درخت AVL در نظر گرفته می‌شود. مقدار عامل متعادل کننده باید برای هر گره در یک درخت AVL برابر با صفر، یک و ‎-۱‎ باشد.

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

ویژگی های درخت AVL در ساختمان داده

هر یک از ویژگی‌های درخت AVL در ساختمان داده در ادامه فهرست شده‌اند.

• AVL هم از تمام خصوصیات ساختار داده درختی پیروی می کند.
• خودمتعادل‌کننده (Self-Balancing) است.
• هر گره مقداری به نام عامل متعادل‌کننده را ذخیره می‌کند که اختلاف ارتفاع زیردرخت سمت چپ و زیر درخت سمت راست است.
• همه گره‌های درخت AVL دارای «عامل متعادل‌کننده» (Balance Factor) با مقادیر 1-، 0 و یا 1 هستند.

درخت سرخ-سیاه در ساختمان داده

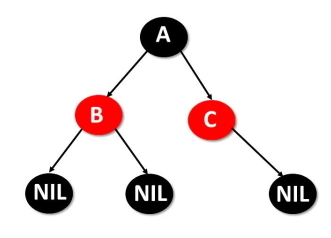
«درخت سرخ-سیاه» (Red-Black Tree) یکی دیگر از انواع درخت در ساختمان داده که یک درخت جستجوی دودویی خود متعادل‌کننده به حساب می‌آید و در آن هر گره یا رنگ قرمز یا سیاه دارد. رنگ گره‌ها برای اطمینان از این مسئله استفاده می‌شود که درخت در طول درج و حذف تقریباً متعادل باقی می‌ماند.

تنها تفاوت درخت سرخ-سیاه با درخت AVL این است که ما نمی‌دانیم چقدر چرخش برای متعادل کردن درخت لازم است. اما در درخت سرخ-سیاه حداکثر دو چرخش برای متعادل کردن درخت مورد نیاز است. این نوع درخت حاوی بیتی است که رنگ قرمز یا سیاه گره را برای اطمینان از تعادل درخت نشان می‌دهد.

فیلم آموزش درخت در نظریه گراف و کاربردها (رایگان) در فرادرس

کلیک کنید

ویژگی های درخت سرخ-سیاه در ساختمان داده

خصلت‌های درخت سرخ-سیاه در ساختمان داده به شرح زیر هستند.

• تمام خصوصیات ساختار داده درخت دودویی را دارد.
• خودمتعادل‌کننده است.
• هر گره یا قرمز یا سیاه است.
• گره ریشه و برگ سیاه است.
• اگر گره قرمز باشد، هر دو فرزند سیاه هستند.
• هر مسیر از یک گره معین به هر یک از گره‌های آن باید از همان تعداد گره سیاه عبور کند.

درخت Splay در ساختمان داده

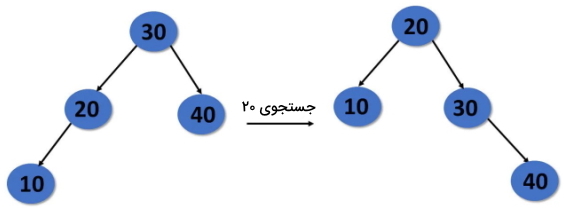
درخت Splay یا گسترده از دیگر انواع درخت در ساختمان داده محسوب می‌شود. درخت اسپلی یک درخت دودویی خودمتعادل کننده است.

ویژگی های درخت Splay در ساختمان داده

خصوصیت‌های درخت Splay در ساختمان داده در ادامه فهرست شده است:

• از ویژگی‌های ساختار داده درختی دودویی پیروی می‌کند.
• خودمتعادل‌کننده است.
• دسترسی مجدد به عناصری که اخیراً به آنها دسترسی پیدا کرده‌اند سریعتر است.

بعد از اینکه عملیاتی مانند درج و حذف انجام شد، درخت Splay وارد عمل می‌شود و انجام عملیات «Splaying» را آغاز می‌کند و به این صورت است که درخت را دوباره مرتب می‌کند، به طوری که عناصر خاص در ریشه درخت قرار می‌گیرند.

درخت Treap در ساختمان داده

تریپ نوعی درخت جستجوی دودویی است که در آن به هر گره یک اولویت عددی تصادفی اختصاص داده می‌شود و گره‌ها با توجه به آن اولویت‌ها به صورت هرمی قرار می‌گیرند.

ویژگی های درخت تریپ در ساختمان داده

ویژگی‌های درخت تریپ در ساختمان داده به شرح زیر هستند:

• هر گره دارای دو مقدار است؛ یک کلید و یک اولویت.
• این نوع درخت از خواص درخت جستجوی دودویی پیروی می‌کند.
• اولویت درخت Treap از خاصیت هرمی پیروی می‌کند.

پیمایش درخت در ساختمان های داده

پیمایش درخت فرآیند بازدید از هر گره و چاپ ارزش آن‌ها است. سه راه برای پیمایش ساختمان داده درخت وجود دارد:

• «پیمایش به‌ترتیب» (In-Order Traversal)
• «پیمایش پیش‌ترتیب» (Pre-Order Traversal)
• «پیمایش پس‌ترتیب» (Post-Order Traversal)

در ادامه به طور مجزا به هر یک از این ۳ روش پیمایش در ساختار درختی پرداخته شده است.

پیمایش درخت به روش به ترتیب

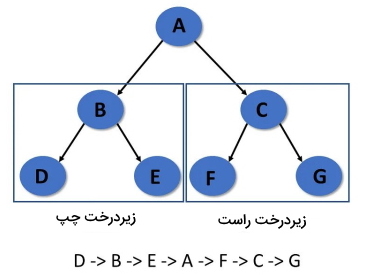
در «پیمایش به‌ترتیب» (In-Order Traversal)، ابتدا زیردرخت سمت چپ، سپس ریشه و بعداً زیردرخت سمت راست بازدید می‌شود.

الگوریتم پیمایش به ترتیب در درخت

هر یک از گام‌های پیمایش درخت در روش In-Order به شرح زیر هستند:

• مرحله 1: به صورت بازگشتی زیر درخت سمت چپ را پیمایش می‌کند.
• مرحله 2: از گره ریشه بازدید می‌شود.
• مرحله 3: به صورت بازگشتی زیر درخت سمت راست پیمایش می‌شود.

پیمایش درخت به روش پیش ترتیب

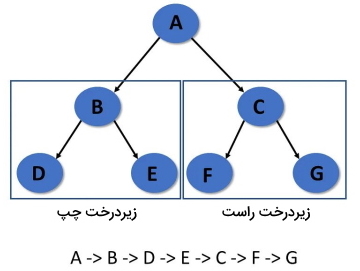
در «پیمایش پیش‌ترتیب» (Pre-Order Traversal)، ابتدا گره ریشه، سپس زیر درخت سمت چپ و در نهایت زیر درخت سمت راست بازدید می‌شود.

الگوریتم پیمایش درخت به روش پیش ترتیب

گام‌های اجرای الگوریتم پیمایش درخت به روش Pre-Order در ادامه فهرست شده‌اند:

• مرحله 1: از گره ریشه بازدید می‌شود.
• مرحله 2: به صورت بازگشتی زیردرخت سمت چپ را پیمایش می‌کند.
• مرحله 3: به صورت بازگشتی زیر درخت سمت راست پیمایش می‌شود.

پیمایش درخت به روش پس ترتیب

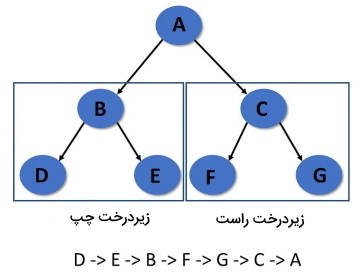
در «پیمایش پس‌ترتیب» (Post-Order Traversal) ابتدا زیردرخت سمت چپ، سپس زیردرخت سمت راست و در نهایت گره ریشه بازدید می‌شود.

الگوریتم پیمایش پس ترتیب

گام‌های پیمایش درخت به روش Post-Order در ادامه آمده است.

• مرحله 1: به صورت بازگشتی زیر درخت سمت چپ را پیمایش کنید.
• مرحله 2: از گره ریشه بازدید کنید.
• مرحله 3: به صورت بازگشتی زیردرخت سمت راست را پیمایش کنید.

سوالات متداول ساختار داده درخت

در این بخش به برخی از سوالات متداول در ارتباط با ساختار داده درخت پرداخته شده است.

چرا درخت یک ساختمان داده غیرخطی به حساب می‌آید؟

ساختار داده درختی، غیرخطی است، زیرا به صورت متوالی ذخیره نمی‌شود. درخت یک ساختمان سلسله‌مراتبی دارد، زیرا عناصر یک درخت در چندین سطح مرتب شده‌اند. بالاترین گره در ساختمان داده درخت به عنوان گره ریشه شناخته می‌شود. هر گره، حاوی داده‌هایی است و داده‌ها می‌توانند از هر نوعی باشند.

ساختمان داده درخت در زندگی واقعی چه کاربردی دارد؟

پایگاه‌های داده ممکن است از ساختمان داده درخت برای «نمایه‌سازی» (Indexing) استفاده کنند. «سرور نام دامنه» (DNS) نیز از ساختارهای درختی استفاده می‌کند. BST در گرافیک کامپیوتری استفاده می‌شود.

درخت کامل چیست؟

درخت دودویی کامل، نوعی درخت دودویی است که در آن هر گره داخلی دقیقاً دو گره فرزند دارد و تمام گره‌های برگ در یک سطح هستند.

چرا از درخت در ساختمان داده استفاده می شود؟

برخلاف آرایه و لیست پیوندی که ساختمان داده‌های خطی محسوب می‌شوند، ساختمان داده درخت، سلسله مراتبی (یا غیر خطی) است. اگر کلیدها را به صورت درختی سازماندهی کنیم، می‌توانیم یک کلید معین را در زمانی سریع‌تر از لیست پیوندی و کندتر از آرایه‌ها جستجو کنیم.

ویژگی های درخت در ساختمان داده چیست؟

درخت یک گراف غیرمدور است و بین هر جفت راس آن، یک مسیر منحصر به فرد جود دارد. درختی با N تعداد راس حاوی (N-1) یال است. رأسی که درجه آن صفر باشد ریشه درخت نامیده می‌شود.

چه عملیاتی را می توان روی درخت انجام داد؟

عملیات معمول روی درخت عملیاتی هستند که در ساختمان داده‌های متوالی نیز وجود دارند که شامل افزودن و حذف عناصر، جستجو، و پیمایش هستند.

انواع درخت در ساختمان داده کدامند و چه کاربردی دارند؟

درخت جستجوی دودویی را می‌توان برای جستجوی یک عنصر در مجموعه‌ای از عناصر به‌کار برد. درختان هرمی برای مرتب‌سازی هرمی استفاده می‌شوند. روترهای مدرن از نوعی درخت به نام Tries برای ذخیره اطلاعات مسیریابی استفاده می کنند. B-Tree و T-Tree بیشتر در پایگاه‌های داده رایج به منظور ذخیره داده‌ها بکار می‌روند.

جمع‌بندی

ساختمان داده درخت شامل مجموعه‌ای از اشیاء یا موجودیت‌های شناخته شده است که به عنوان گره‌های درخت تعریف می‌شوند. این گره‌ها به صورت سلسله مراتبی و مرتبط به یکدیگر نمایش داده می‌شوند. درخت یک ساختمان داده بازگشتی به حساب می‌آید. بازگشتی بودن درخت به این دلیل است که هر درخت شامل چندین زیردرخت می‌شود، زیرا هر گره در درخت به عنوان ریشه درخت دیگری است که آن را به یک زیردرخت تبدیل می‌کند.

در این مطلب به برخی از کاربردهای مهم درخت از جمله پیمایش، جستجو، تصمیم‌گیری و یادگیری ماشین اشاره شد و همچنین به موضوع مهم انواع درخت در ساختمان داده هم پرداختیم. از جمله رایج ترین انواع درخت در ساختمان داده شامل درخت دودویی، درخت جستجوی دودویی، درخت AVL و درخت سرخ-سیاه هستند.