حجم استوانه و محاسبه آن — به زبان ساده

در آموزش‌های پیشین از مجموعه مطالب ریاضی مجله فرادرس، با روش محاسبه حجم برخی از اشکال و احجام هندسی از قبیل مخروط و کره آشنا شدیم. در این آموزش، فرمول محاسبه حجم استوانه را همراه با حل چند مثال بیان خواهیم کرد.

استوانه چیست؟

اگر به شکل یک قوطی نوشابه یا فرش لوله شده دقت کرده باشید، خواهید دید که شبیه یک استوانه است. «استوانه» یا سیلندر (Cylinder) یکی از حجم‌های هندسی است که دو دایره موازی و هم‌اندازه در بالا و پایین دارد.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

این دایره‌ها «قاعده» (Base) استوانه نامیده می‌شوند. فاصله بین دو قاعده را نیز «ارتفاع» (Height) می‌گوییم و معمولاً با $$h$$ نشان می‌دهیم. اگر قاعده‌های بالا و پایین استوانه در یک راستا باشند، استوانه را قائم و اگر بر هم منطبق نباشند، استوانه را مایل می‌نامیم. شکل زیر استوانه مایل و قائم را نشان می‌دهد.

محاسبه حجم استوانه

برای محاسبه حجم استوانه باید طول ارتفاع و مساحت قاعده آن را داشته باشیم. فرض کنید مساحت قاعده و ارتفاع استوانه‌ای به ترتیب برابر با $$A$$ و $$h$$ باشند. در این صورت اندازه حجم استوانه برابر است با:

$$\large V = A h$$

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

همان‌طور که می‌دانیم، قاعده‌های استوانه دایره‌ای هستند و بنابراین، مساحت قاعده استوانه همان مساحت دایره است. در نتیجه، به طور خلاصه می‌توان چنین گفت که مساحت استوانه مایل یا قائم با ارتفاع $$h$$ و شعاع قاعده $$r$$ برابر است با:

$$\large \boxed {V = \pi r ^ 2 h }$$

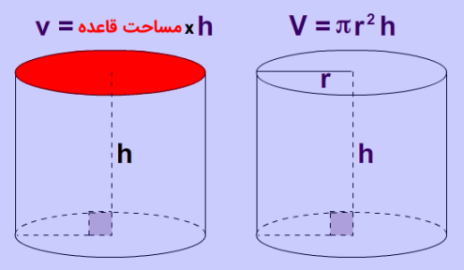
نکته: ممکن است به جای شعاع دایره، طول قطر آن را داشته باشیم که در این موارد، ابتدا قطر را تقسیم بر دو کرده و شعاع را به دست می‌آوریم، سپس از فرمول بالا استفاده می‌کنیم.

مثال های حجم استوانه

در این بخش، چند مثال را از محاسبه حجم استوانه بررسی می‌کنیم.

مثال اول حجم استوانه

حجم استوانه شکل زیر را به دست آورید.

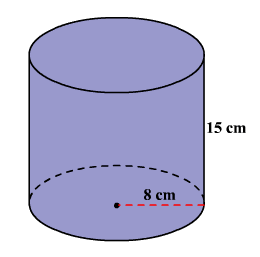
حل: با توجه به اینکه ارتفاع و شعاع قاعده استوانه را داریم، به سادگی می‌توانیم حجم آن را به دست آوریم:

$$\large V = \pi r ^ 2 h = \pi \times (8^2)\times 15 = 3.14\times 64\times 15 = 3014.4\; \text{cm}^3$$

مثال دوم حجم استوانه

شکل زیر بخشی از یک لوله فلزی را نشان می‌دهد. شعاع داخلی لوله 2 سانتی‌متر، شعاع خارجی آن 2٫4 سانتی‌متر و طول لوله 10 سانتی‌متر است. حجم فلز مورد استفاده را پیدا کنید.

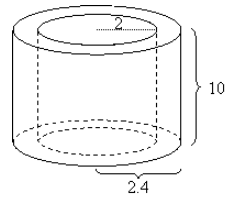
حل: سطح مقطع لوله یک حلقه است که مساحت آن از تفاضل مساحت دایره بزرگ و کوچک به دست می‌آید (شعاع دایره بزرگ را $$R$$ و شعاع دایره کوچک را $$r$$ در نظر می‌گیریم):

$$\large A = \pi R^2-\pi r^ 2 = \pi [R^2-r^2]=\pi [2.4^2-2^2]=5.53\; \text{cm}^ 2$$

با توجه به اینکه طول لوله یا همان ارتفاع $$h$$ را داریم، می‌توانیم حجم فلز را محاسبه کنیم:

$$\large V = A h = 5.53\times 10 = 55.3 \; \text{cm}^3$$

مثال سوم حجم استوانه

قطر استوانه‌ای برابر با ۶ سانتی‌متر و ارتفاع آن ۱۰ سانتی‌متر است. حجم این استوانه را برحسب لیتر به دست آورید. برای حل مثال به ادامه این مطلب از مجله فرادرس توجه کنید.

حل: با توجه به اینکه قطر را داریم، می‌توانیم شعاع را با نصف کردن آن به دست آوریم. بنابراین، قطر برابر با $$r= \frac 6 2 =3\;\text{cm}$$ و ارتفاع $$h = 10\; \text{cm}$$ است. در نتیجه، حجم استوانه برابر است با:

$$\large V = \pi r ^ 2 h = \pi\times 3^2\times 10= 3.14\times 9\times 10=282.6 \;\text{cm}^3$$

همان‌طور که می‌بینیم، حجم بالا برحسب سانتی‌متر مکعب است و باید آن را به لیتر تبدیل کنیم. با توجه به مطالبی که در آموزش «تبدیل واحد حجم — به زبان ساده (+ دانلود فیلم آموزش رایگان)» از مجله فرادرس به آن اشاره کردیم، حجم استوانه برحسب لیتر به صورت زیر محاسبه می‌شود:

$$\large V = 282.6 \;\text{cm}^3 \times \frac {0.001\; \text{L}}{1 \;\text{cm}^3}= 0.2826\; \text{L}$$

مثال چهارم حجم استوانه

در شکل زیر، $$R=2 \;\text{cm}$$ و $$h = 4 \; \text{cm}$$ است. حجم این استوانه را محاسبه کنید.

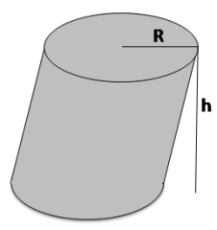
حل: فرمول حجم استوانه مایل نیز برابر با مساحت قاعده ضرب در ارتفاع است و داریم:

$$\large V = \pi R ^ 2 h = \pi \times (2^2)\times 4 = 3.14\times 4\times 4 = 50.24\; \text{cm}^3$$