جستجوی عمقی در هوش مصنوعی – توضیح الگوریتم به زبان ساده

الگوریتم‌های جستجو در «ساختمان داده‌‌ها» (Data Structures) یکی از موضوعات مهم در مباحث طراحی الگوریتم و برنامه نویسی محسوب می‌شوند. این نوع الگوریتم‌‌ها برای پیدا کردن مقادیر خاصی از اطلاعات ذخیره شده در ساختار داده‌های مختلف نظیر درخت و گراف کاربرد دارند. الگوریتم «جستجوی عمقی» (Depth First Search | DFS) به عنوان یکی از الگوریتم‌های جستجوی رایج در هوش مصنوعی تلقی می‌شود که قصد داریم این مطلب از مجله فرادرس را به آن اختصاص دهیم.

در مطلب حاضر در ابتدا به توضیح الگوریتم‌های پیمایش گراف و معرفی الگوریتم جستجوی عمقی می‌پردازیم و پس از توضیحاتی پیرامون ویژگی‌ها، کاربردها مزایا و معایب روش DFS، با ارائه یک مثال ساده، مراحل این الگوریتم را برای پیدا کردن پاسخ مسئله شرح می‌دهیم.

الگوریتم پیمایش گراف چیست ؟

در ساختمان داده‌هایی نظیر درخت و گراف از الگوریتم‌های پیمایش برای پیدا کردن مقداری خاص استفاده می‌شوند. در این نوع ساختار داده‌ها، حلقه‌ای وجود ندارد و در روال پیمایش، هر راس از درخت یا گراف با ترتیبی خاص مورد بررسی قرار می‌گیرند که آیا دربرگیرنده مقدار «هدف» (Target) هستند و عملیات پیمایش خاتمه یابد یا باید روال جستجو ادامه پیدا کند؟

برای انجام روال پیمایش، می‌توان درخت یا گراف را به دو شیوه کلی پیمایش کرد که در ادامه به آن‌ها اشاره شده است:

• روش «جستجوی اول سطح» (Breadth-First Search) یا همان الگوریتم BFS
• روش «جستجوی اول عمق» (Depth-First Search) یا الگوریتم DFS

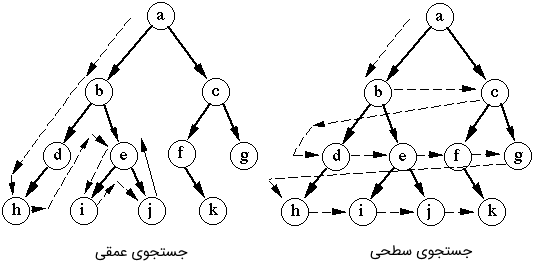
در مطلب پیشین از مجله فرادرس با عنوان «الگوریتم BFS» روال پیمایش گراف را به همراه مثال کاربردی توضیح دادیم. در مطلب فعلی قصد داریم روال جستجوی درخت یا گراف را با روش جستجوی DFS توضیح دهیم و برای درک این الگوریتم مثالی ساده از آن ارائه کنیم.

الگوریتم جستجوی عمقی چیست ؟

از الگوریتم جستجوی DFS در هوش مصنوعی به منظور پیمایش ساختار داده‌هایی نظیر درخت و گراف استفاده می‌شود. با کمک این نوع پیمایش، روال جستجوی درخت یا گراف به‌صورت عمقی انجام می‌شود. روند جستجوی الگوریتم از گره ریشه درخت شروع می‌شود و برای جستجوی گراف می‌توان از هر گره‌ای کار پیمایش را آغاز کرد.

به منظور نگهداری مقادیر گره‌های ساختمان‌ داده‌های درخت یا گراف در روال جستجوی عمقی، از ساختار داده پشته استفاده می‌شود تا بتوان مسیر جستجو را دنبال کرد. در بخش‌های بعدی این مطلب، به یک مثال کاربردی از جستجوی عمقی در هوش مصنوعی می‌پردازیم تا به درک این روند پیمایش کمک کند.

کاربرد الگوریتم جستجوی عمقی در هوش مصنوعی

کاربردهای الگوریتم جستجوی اول عمق در هوش مصنوعی را می‌توان به‌صورت فهرست زیر خلاصه کرد:

فیلم آموزش ساختمان داده ها با پایتون

کلیک کنید

• از الگوریتم جستجوی DFS در مرتب‌سازی توپولوژی استفاده می شود.
• الگوریتم جستجوی عمقی در هوش مصنوعی در پیدا کردن مسیر بین دو راس کاربرد دارد.
• از روش پیمایش جستجوی اول عمق برای تشخیص وجود حلقه در گراف استفاده می‌شود. زمانی در گراف حلقه وجود دارد که یک راس را دو بار در پیمایش ملاحظه کنیم.
• از الگوریتم جستجوی DFS برای تشخیص نوع «گراف دو بخشی» (Bipartite Graph) استفاده می‌شود.
• از الگوریتم جستجوی اول عمق در مسائل و معماهایی استفاده می‌شود که تنها دارای یک راه‌حل هستند.

مراحل الگوریتم جستجوی اول عمق چیست ؟

به منظور پیاده‌سازی الگوریتم جستجوی اول عمق، از ساختار داده پشته و یک لیست خالی استفاده می‌کنیم و مراحل زیر را دنبال می‌کنیم:

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

1. پشته‌ و لیستی را به اندازه تعداد گره‌های گراف یا درخت ایجاد کنید.
2. گره‌ای ریشه را از درخت انتخاب و آن را به لیست اضافه کنید. اگر از ساختمان داده گراف استفاده می‌کنید، می‌توانید یکی از گره‌ها را به عنوان نقطه شروع جستجو به لیست اضافه کنید.
3. تمامی گره‌های مجاور (گره‌های فرزند) گره دیده شده را در بالای پشته قرار دهید.
4. به ترتیب گره‌های موجود در پشته را خارج کرده و به لیست اضافه کنید.
5. مرحله ۳ و ۴ را آنقدر تکرار کنید تا پشته خالی شود.

در ادامه، شبه کد الگوریتم جستجوی DFS را ملاحظه می‌کنید:

در بخش بعدی، به ارائه یک مثال کاربردی از الگوریتم DFS می‌پردازیم.

مثال کاربردی از الگوریتم DFS

در این بخش از مطلب حاضر مجله فرادرس، به توضیح یک مثال کاربردی برای درک بهتر روال الگوریتم جستجوی DFS می‌پردازیم.

گراف و پشته خالی زیر را در نظر بگیرید. از یک لیست نیز برای ذخیره کردن گره‌های ملاحظه شده استفاده می‌شود.

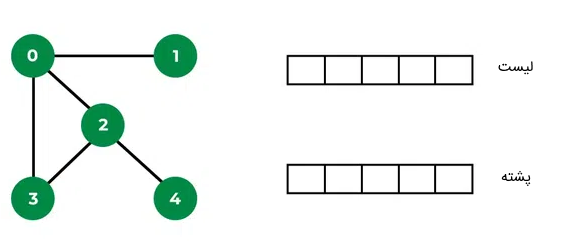
مرحله اول: گره ۰ از گراف بالا را به عنوان نقطه آغاز پیمایش جستجوی اول عمق در نظر می‌گیریم و این گره را به لیست اضافه می‌کنیم:

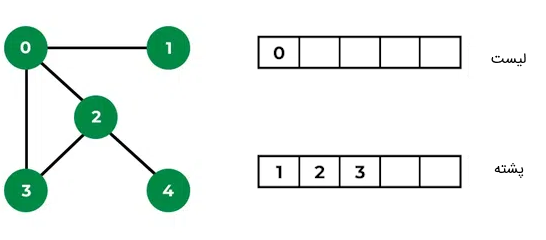
مرحله دوم: یکی از گره‌‌هایی را که در مجاورت با گره ۰ در گراف وجود دارد و در بالای پشته ذخیره شده است، درون لیست ذخیره می‌کنیم. در این مرحله گره ۱ را اضافه کردیم:

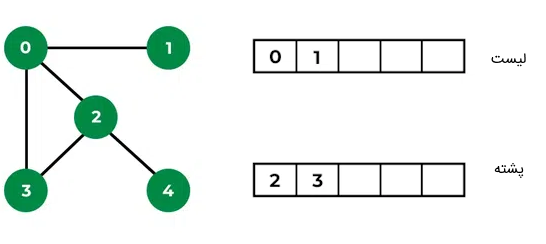
مرحله سوم: حال، گره بعدی را از پشته به درون لیست اضافه می‌کنیم و اگر این گره دارای فرزند است، آن را در بالای پشته قرار می‌دهیم. در این مرحله، عدد ۲ را از بالای پشته خارج کرده و در لیست قرار می‌دهیم و فرزند آن را که عدد ۴ است، در بالای پشته ذخیره می‌کنیم:

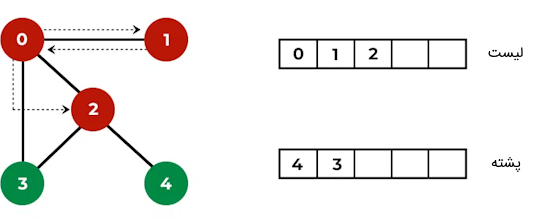
مرحله چهارم: حال، گره بالای پشته (یعنی گره ۴) را می‌خوانیم و آن را درون لیست قرار می‌دهیم. اگر این گره فرزندی داشته باشد، در بالای پشته قرار می‌گیرد.

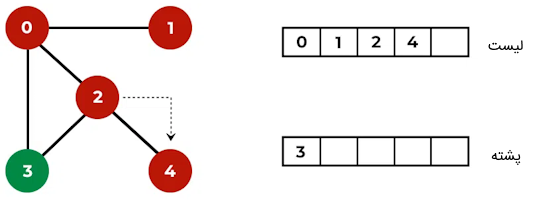
مرحله پنجم: گره بالای پشته (گره ۳) خارج و به لیست اضافه می‌شود. اگر گره ۳ فرزندی داشته باشد، درون پشته اضافه می‌شود. با توجه به این که تمام گره‌های گراف در لیست گره‌های مشاهده شده قرار گرفته‌اند، پیمایش جستجوی DFS به اتمام می‌رسد و در این مرحله پشته نیز دارای هیچ مقداری نیست.

پیچیدگی زمانی و پیچیدگی فضایی الگوریتم جستجوی عمقی چیست؟

پیچیدگی زمانی الگوریتم جستجوی عمقی برابر با O(V + E) است. مقدار V برابر با تعداد راس‌ها و مقدار E برابر با تعداد یال‌های گراف است. پیچیدگی فضایی الگوریتم جستجوی اول عمق نیز برابر با O(V) است زیرا در بدترین وضعیت، الگوریتم باید تمام راس‌های گراف را برای پیدا کردن مقدار هدف در حافظه ذخیره کند.

فیلم آموزش مروری بر پیچیدگی محاسبات Computational Complexity در فرادرس

کلیک کنید

مزایای الگوریتم جستجوی اول عمق

الگوریتم جستجوی هوش مصنوعی اول عمق دارای مزیت‌هایی است که در ادامه به دو مورد از مهم‌ترین ویژگی‌های مثبت این الگوریتم اشاره شده است:

• الگوریتم جستجوی اول عمق به حافظه کم‌تری نسبت به الگوریتم جستجوی اول سطح احتیاج دارد زیرا در این روش از الگوریتم، تنها کافی است مسیر ریشه تا گره فعلی در پشته ذخیره شود.
• این روش جستجو ممکن است در برخی مسائل خیلی سریع به پاسخ برسد و به همین دلیل میزان زمان و فضای مورد استفاده الگوریتم بسیار کاهش خواهد یافت.

معایب الگوریتم DFS چیست ؟

الگوریتم DFS علاوه‌بر ویژگی‌های مثبت، دارای معایبی نیز است که در ادامه به برخی از مهم‌ترین معایب آن اشاره می‌کنیم:

• از معایب اصلی الگوریتم جستجوی اول عمق این است که روال جستجو در عمق درخت ممکن است بی‌نهایت طول بکشد. البته می‌توان برای جستجو در عمق درخت مرز قائل شد تا جستجوی عمقی از یک سطح مشخص بیشتر پیش نرود. اما در این حالت ممکن است الگوریتم نتواند جواب مسئله را پیدا کند زیرا بخشی از مسیر را در روند پیمایش نادیده می‌گیرد.
• تضمین قطعی وجود ندارد که با الگوریتم جستجوی DFS به پاسخ مسئله برسیم.
• چنانچه بیش از یک پاسخ برای مسئله وجود داشته باشد، این تضمین وجود ندارد که پاسخ الگوریتم جستجوی اول عمق، بهینه‌ترین راه‌حل باشد.

پیاده سازی الگوریتم جستجوی عمقی در هوش مصنوعی

در این بخش، نحوه پیاده‌سازی الگوریتم DFS را برای مثال گرافی ملاحظه می‌کنید که در بخش قبل ارائه کردیم. قطعه کدهای ارائه شده به ۶ زبان برنامه نویسی C ،C++‎ ،C#‎ ،جاوا، جاوا اسکریپت و پایتون هستند که خروجی تمامی این قطعه کدها، یکسان است.

پیاده سازی الگوریتم DFS با زبان برنامه نویسی ++C

در قطعه کد زیر، نحوه پیاده‌سازی الگوریتم جستجوی اول عمق را با زبان برنامه نویسی ++C ملاحظه می‌کنید.

خروجی قطعه کد بالا در ادامه دیده می‌شود:

Following is Depth First Traversal (starting from vertex 2) 
2 0 1 3 

پیاده سازی الگوریتم جستجوی عمقی با زبان برنامه نویسی جاوا

در قطعه کد زیر، نحوه پیاده‌سازی الگوریتم جستجوی DFS در هوش مصنوعی را با زبان برنامه نویسی جاوا ملاحظه می‌کنید.

پیاده سازی الگوریتم جستجوی اول عمق با زبان برنامه نویسی پایتون

در قطعه کد زیر، نحوه پیاده‌سازی الگوریتم پیمایش عمقی در هوش مصنوعی را با زبان برنامه نویسی پایتون ملاحظه می‌کنید.

پیاده سازی الگوریتم جستجوی هوش مصنوعی اول عمق با زبان برنامه نویسی C#‎

در قطعه کد زیر، نحوه پیاده‌سازی الگوریتم پیمایش عمقی در هوش مصنوعی را با زبان برنامه نویسی C#‎ ملاحظه می‌کنید.

پیاده سازی الگوریتم جستجوی اول عمق با زبان برنامه نویسی جاوا اسکریپت

در قطعه کد زیر، نحوه پیاده‌سازی الگوریتم پیمایش اول عمق در هوش مصنوعی را با زبان برنامه نویسی جاوا اسکریپت ملاحظه می‌کنید.

جمع‌بندی

الگوریتم‌های جستجوی هوش مصنوعی به منظور پیدا کردن مقداری خاص درون ساختمان داده‌های مختلف مورد استفاده قرار می‌گیرند. یکی از پرکاربردترین الگوریتم‌های پیمایشی، الگوریتم جستجوی عمقی است که کاربرد مختلفی در مسائل گوناگون دارد. در این مطلب از مجله فرادرس سعی داشتیم به این پرسش پاسخ دهیم که الگوریتم DFS چیست و چه ویژگی‌هایی دارد. سپس، با ارائه یک مثال کاربردی، مراحل کار این الگوریتم را شرح دادیم تا درک آن برای خوانندگان ساده باشد.