تابع پیچش (Convolution) در OpenCV پایتون — پیاده سازی گام به گام

در مطالب قبلی مجله فرادرس، به اپراتور سوبل در پایتون پرداختیم و فیلترهای مورد نیاز را گام به گام پیادهسازی و مفهوم آنها را بررسی کردیم. در این مطلب سعی میکنیم عمل پیچش در پایتون را بررسی کرده و با استفاده از کتابخانه OpenCV از آن استفاده کنیم.
فرآیند پیچش (Convolution) چگونه است؟
در عمل پیچش (Convolution)، فیلتری روی تمامی موقعیتهای ممکن روی یک تصویر قرار میگیرد و هر ضریب موجود در فیلتر، به مقدار پیکسل متناظر ضرب شده، مقادیر حاصل جمع شده و تصویر خروجی حاصل میشود. در تصویر زیر روش انجام این فرآیند را میبینیم.
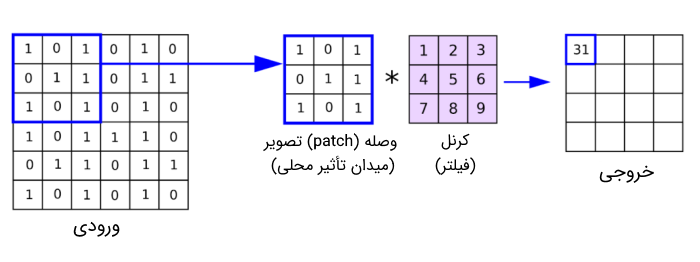
توجه داشته باشید که عملگر «*» موجود بین ماتریس وصله تصویر (Image Patch) و کرنل یا هسته (Kernel) نشاندهنده ضرب متناظر است.
برای عمل پیچش برخی پارامترهای دیگر نیز قابل تعریف هستند، مانند:
- «گام» (Stride): این عدد نشاندهنده میزان حرکت فیلتر پس از هر بال اعمال است که برای پیچش معمولی برابر با ۱ است.
- «حاشیه» (Padding): این عدد تعیین میکند که چند لایه پیکسل خالی با مقدار ۰ به اطراف تصویر اولیه افزوده شود. با تنظیم Padding میتوان اندازه تصویر خروجی را با تصویر ورودی یکسان کرد. برای مثال، اگر از یک فیلتر ۳×۳ استفاده کنیم، یک Padding با اندازه ۱ باعث میشود تصویر خروجی هماندازه با تصویر اولیه شود.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی پیچش در پایتون
در این بخش، پیادهسازی پیچش در پایتون را برای دو کتابخانه OpenCV و Scipy بیان میکنیم.
پیاده سازی پیچش در پایتون با استفاده از OpenCV
ابتدا یک تصویر انتخاب و در کنار فایل برنامه قرار میدهیم.
توجه: برای بزرگنمایی تصاویر این آموزش، روی آنها کلیک کنید.

حال میتوانیم کتابخانههای مورد نیاز را فراخوانی کنیم:
1import cv2 as cv
2import numpy as np
3import scipy.signal as sigاین کتابخانهها بهترتیب برای اعمال زیر کاربرد خواهند داشت:
- پردازش روی تصویر و نمایش آنها
- کار با آرایهها و محاسبات برداری
- پردازش سیگنال
حال تصویر انتخابشده را با استفاده از کتابخانه OpenCV میخوانیم (نام این تصویر Picture_1 با پسوند jpg است):
1Image = cv.imread('Picture_1.jpg')برای نمایش تصویر میتوان بهشکل زیر نوشت:
1cv.imshow('Original Image', Image)
2cv.waitKey()
3cv.destroyAllWindows()حال میتوانیم برخی از فیلترهای پرکاربرد را اعمال و نتایج را مشاهده کنیم:
۱. فیلتر Sharpening
این فیلتر باعث افزایش وضوح (Sharp) نواحی در تصویر میشود. برای اعمال این فیلتر، بهشکل زیر مینویسیم:
1F1 = np.array([[ 0, -1, 0],
2 [-1, +5, -1],
3 [ 0, -1, 0]])
4
5G1 = cv.filter2D(Image, -1, F1)برای نمایش و ذخیره تصویر حاصل نیز مینویسیم:
1cv.imshow('Sharpening Filter Result', G1)
2cv.imwrite('Sharpening Filter Result.jpg', G1)
3cv.waitKey()
4cv.destroyAllWindows()پس از اجرای کد فوق، نتیجه زیر حاصل میشود.

به این ترتیب، مشاهده میکنیم که نواحی ریز و برخی حاشیهها، وضوح بیشتری پیدا کردهاند.
۲. فیلتر Bluring
این فیلتر برای ایجاد حالت تارشدگی روی تصویر ایجاد میشود. فیلتر Bluring بهنوعی یک میانگین متحرک ساده (Simple Moving Average) است که روی دو بعد کار میکند. برای اعمال این فیلتر بهشکل زیر عمل میکنیم:
1F2 = np.ones((3, 3)) / 9
2
3G2 = cv.filter2D(Image, -1, F2)
4
5cv.imshow('Blurint Filter Result', G2)
6cv.imwrite('Bluring Filter Result.jpg', G2)
7cv.waitKey()
8cv.destroyAllWindows()و تصویر زیر حاصل میشود.

به این ترتیب، محوشدگی در تصویر بهخوبی مشاهده میشود.
۳. فیلتر Outline
این فیلتر برای مشخص کردن حاشیهها و مرز به اشیا در تصویر استفاده میشود. برای پیادهسازی آن میتوانیم بهشکل زیر عمل کنیم:
1F3 = np.array([[-1, -1, -1],
2 [-1, +8, -1],
3 [-1, -1, -1]])
4
5G3 = cv.filter2D(Image, -1, F3)
6
7cv.imshow('Outline Filter Result', G3)
8cv.imwrite('Outline Filter Result.jpg', G3)
9cv.waitKey()
10cv.destroyAllWindows()که تصویر زیر در خروجی ایجاد خواهد شد.

به این ترتیب، واکنش فیلتر به مرزها کاملاً مشهود است.
اگر این فیلتر را بهشکل زیر تغییر دهیم:
تصویر زیر حاصل میشود.

به این ترتیب، مشاهده میکنیم که تصویر با حفظ رنگ اصلی خود، مرزها را نیز مشخص کرده است. علت این اتفاق، در مجموعِ اعداد فیلتر نهفته است. اگر مجموع اعداد یک فیلتر برابر ۰ باشد، تصویر خروجی غالباً در طیف خاکستری خواهد بود، اما اگر مجموع آن ۱ یا بیشتر باشد، رنگ اصلی تصویر نیز حفظ خواهد شد.
۴. فیلتر Emboss
این فیلتر برای برجسته کردن تصویر و بهنوعی مشتقگیری در جهتی خاص از تصویر استفاده میشود. برای مثال، فیلتر آوردهشده در بالا، نسبت به مرزهایی با زاویه نزدیک به ۴۵ و ۲۲۵ درجه حساسیت بالایی دارد. این فیلترها شامل خانوادهای از فیلترها میشوند که با توجه به نیاز میتوان آنها را طراحی و استفاده کرد.
برای پیادهسازی این فیلتر، مینویسیم:
1F5 = np.array([[-2, -1, 0],
2 [-1, +1, +1],
3 [ 0, +1, +2]])
4
5G5 = cv.filter2D(Image, -1, F5)
6
7cv.imshow('Emboss Filter Result', G5)
8cv.imwrite('Emboss Filter Result.jpg', G5)
9cv.waitKey()
10cv.destroyAllWindows()که شکل زیر را خواهیم داشت.

به این ترتیب، واکنش این فیلتر به زوایای ۴۵ و ۲۲۵ درجه کاملاً معلوم است.
۵. فیلتر Sobel
این دو فیلتر نیز بهنوعی نقش گرادیان را ایفا میکنند. میتوان آنها را جزو فیلترهای Emboss در نظر گرفت. فیلتر اول در جهت افقی مشتقگیری میکند و فیلتر دوم در جهت عمودی.
برای پیادهسازی این دو فیلتر، به شکل زیر عمل میکنیم:
1F6 = np.array([[-1, 0, +1],
2 [-2, 0, +2],
3 [-1, 0, +1]])
4
5G6 = cv.filter2D(Image, -1, F6)
6
7cv.imshow('Sobel(X) Filter Result', G6)
8cv.imwrite('Sobel(X) Filter Result.jpg', G6)
9cv.waitKey()
10cv.destroyAllWindows()
11
12
13F7 = np.array([[+1, +2, +1],
14 [ 0, 0, 0],
15 [-1, -2, -1]])
16
17G7 = cv.filter2D(Image, -1, F7)
18
19cv.imshow('Sobel(Y) Filter Result', G7)
20cv.imwrite('Sobel(Y) Filter Result.jpg', G7)
21cv.waitKey()
22cv.destroyAllWindows()در خروجی بهترتیب دو تصویر زیر حاصل میشود.

و تصویر دوم در زیر آورده شده است.

مشاهده میکنیم که تصویر اول، برخی خطوط عمودی را بهتر تشخیص داده که با توجه به ذات آن، کاملاً توجیهپذیر است.
برای ترکیب دو تصویر و بهترین عملکرد در تشخیص حاشیهها، میتوان دو خروجی را باهم ادغام یا از فیلتر متفاوتی استفاده کرد.
همچنین میتوان خروجی یک فیلتر را بهعنوان یک ورودی فیلتری دیگر استفاده کرد:
1G8 = cv.filter2D(G6, -1, F7)
2
3cv.imshow('Sobel(Y)(Sobel(X)) Filter Result', G8)
4cv.imwrite('Sobel(Y)(Sobel(X)) Filter Result.jpg', G8)
5cv.waitKey()
6cv.destroyAllWindows()در این حالت نیز تصویر زیر حاصل میشود.

به این ترتیب، میبینیم که فیلتر ترکیبی از رفتار دو فیلتر سوبل را داراست.
پیاده سازی پیچش در پایتون با استفاده از Scipy
توجه داشته باشید که بهجای کتابخانه OpenCV میتوان از کتابخانه Scipy نیز بهشکل زیر استفاده کرد:
1G = sig.convolve(Image, F)از این تابع میتوان برای سیگنالهای تکبعدی و یا با ابعاد بالاتر نیز استفاده کرد.
جمعبندی پیاده سازی پیچش در پایتون
در این مطلب به بررسی دقیقتر عمل پیچش و ویژگی برخی فیلترهای مهم پرداختیم. برای مطالعه بیشتر، میتوان پاسخ پرسشهای زیر را بررسی کرد:
- آیا جز ترکیب خطی از پیکسلهای ورودی، میتوان از توابعی دیگر مانند Min, Max, ReLU, Sigmoid استفاده کرد؟ چگونه میتوان این عمل را انجام داد؟
- در معماری «شبکههای عصبی پیچشی» (Convolutional Neural Networks)، به جز لایه پیچش، از چه لایههای دیگری استفاده میشود؟
- چگونه میتوان بهترین فیلتر را برای مجموعه داده انتخاب کرد؟












