فرادرسبارگذاری متحرک در تیرها — به زبان ساده
در مطلب نیروی برشی و گشتاور خمشی نحوه ترسیم نمودار نیرو‌های برشی و گشتاور خمشی برای تیری تحت بارگذاری را توضیح دادیم. در مطلب مذکور دیدیم که ماکزیمم مقدارِ گشتاور در نقطه‌ای با نیروی برشی صفر رخ می‌دهد. جرثقیل و خودرو‌های عبوری از روی پل‌ها معروف‌ترین نمونه‌های بارگذاری متحرک در تیرها محسوب می‌شوند.
تک بارِ متحرک
در اولین حالت، باری به‌صورت تک نیرو را در نظر بگیرید که روی یک تیر در حال حرکت است. با توجه به مطلب نیروی برشی و گشتاور خمشی می‌توان گفت که گشتاور هنگامی ماکزیمم است که نیرو در وسط قرار داشته باشد و نیروی برشی نیز زمانی ماکزیمم است که بار در نزدیکی یکی از تکیه‌گاه‌ها قرار گیرد.
در شکل زیر محل قرار‌گیری نیروی $$ P $$ برای ماکزیمم شدن نیروی برشی و گشتاور خمشی نشان داده شده است.
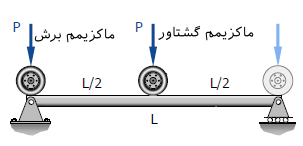
مقادیر نیرو و گشتاور ماکزیمم برابرند با:
$$ \large M _{ m a x } = \dfrac { P L } { 4 } \, \, \text {and}\,\,V _ {max} = P $$
دو بار متحرک
برای بار متحرک قرار گرفته روی یک تیر، حالتی را در نظر می‌گیریم که در آن دو بار به تیر وارد می‌شوند. همچنین یکی از بار‌ها بزرگ‌تر از دیگری است. در شکل زیر تیر به همراه این دو بار نشان داده شده‌اند.
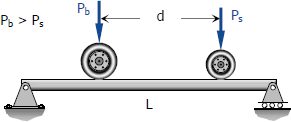
در این حالت نیز ماکزیمم مقدارِ نیروی برشی در تکیه‌گاه‌ها زمانی رخ می‌دهد که نیروی بزرگ‌تر روی تکیه‌گاه قرار داشته باشد. همچنین در این حالت مقدار ماکزیممم گشتاور برابر است با:
$$ \large M _ { m a x } = \dfrac { ( P L - P_s d ) ^ 2 } { 4 P L } $$
توجه داشته باشید که $$ p _ s $$ نشان‌دهنده نیروی کوچک‌تر، $$ p _ b $$، نیروی بزرگ‌تر و $$ p $$ کل نیرو است ($$ P = P _ s + P _ b $$).
سه یا چند بار متحرک
در حالتی عمومی، گشتاور خمشیِ ایجاد شده در نتیجه یک بار، زمانی ماکزیمم است که مرکز تیر بین بار و برآیند بار‌ها قرار گرفته باشد. معمولا طبق این قانون گشتاور ماکزیمم در نتیجه هریک از بار‌ها بدست آمده و بیشترین مقدار آن به‌عنوان مقدار طراحی در نظر گرفته می‌شود.
بیشترین مقدار نیروی برشی نیز در عکس‌العمل زمانی رخ می‌دهد که برآیند بار‌های وارد شده به تیر در نزدیک‌ترین موقعیت ممکن به تکیه‌گاه‌ها باشند. بنابراین در حالتی که بزرگ‌ترین نیرو روی تکیه‌گاه قرار می‌گیرد نیز می‌توان گفت احتمال رخ دادن ماکزیمم نیروی برشی در تکیه‌گاه وجود دارد.
مثال ۱
مطابق با شکل زیر تیری را در نظر بگیرید که دو بارِ $$40 kN$$ و $$60 kN$$ به آن وارد می‌شوند. فرض کنید دو بار در فاصله $$5$$ متری از هم قرار گرفته‌‌اند. همچنین طول کل تیر برابر با $$10$$ متر است (توجه داشته باشید که فاصله دو بار ثابت بوده اما آن‌ها می‌توانند روی تیر حرکت کنند). با این فرضیات، بیشترین نیروی برشی و گشتاور خمشی وارد شده به تیر را بدست آورید.
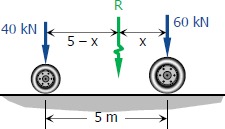
در اولین قدم دو نیرو را با نیروی معادل $$ R $$ جایگزین می‌کنیم. در قدم بعد، می‌توان فاصله $$x$$ را از لبه سمت راست در نظر گرفته و گشتاور معادل نیروی برآیند را در آن بدست آورد. با برابر قرار دادن این گشتاور با گشتاور ناشی از وارد شدن نیروی سمت چپ، اندازه $$ x $$ بدست می‌آید.
$$ \large R = 40 + 60 = 100 \, \text {kN} $$
$$ \large x R = 40 ( 5 ) $$
$$ x = 200 / R $$
$$ x = 200/100 $$
$$ x = 2 \, \text {m} $$
به‌منظور بدست آوردن ماکزیمم مقدار گشتاور، در ابتدا عکس‌العمل $$ R _ 1 $$ را بدست می‌آوریم. لذا داریم:
$$ \large \Sigma M _ { R 2 } = 0 $$
$$ \large 10 R _ 1 = 3 . 5 ( 100 ) $$
$$ \large R _ 1 = 35 \, \text{kN} $$
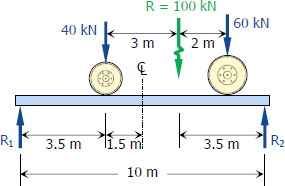
از طرفی همان‌طور که عنوان شد، ماکزیمم گشتاور ناشی از هر نیرو، بین آن نیرو و نیروی برآیند است. بنابراین در فاصله $$3.5$$ از سمت راست، ماکزیمم مقدار گشتاور رخ می‌دهد.
$$ \large M _ { m a x } = 3.5 R _ 1 = 3.5 × 35 =122.5 \ \ k N . m $$
دقیقا به روشی مشابه، گشتاور ماکزیمم ناشی از نیروی $$60 \ kN$$ نیز به صورت زیر قابل محاسبه است.
$$ \large \Sigma M _ { R _ 1 } = 0 $$
$$ \large 1 0 R _ 2 = 4 ( 100 ) $$
$$ \large R _ 2 = 40 \, \text {kN} $$
ماکزیمم مقدار گشتاور نیز مشابه با نیروی قبل برابر است با:
$$ \large M _ { m a x } = 4 R _ 2 = 4 × 40 =160 \ \ k N . m $$
تاکنون ماکزیمم گشتاور ایجاد شده در نتیجه هریک از بار‌ها بدست آمد. اما پاسخ درست، پاسخ بزرگ‌تر است. لذا بیشترین مقدار گشتاور برابر است با:
$$ \large M _ { m a x } = 160 \, \text{kN}\cdot\text{m} \,\,$$
ماکزیمم مقدار نیروی برشی نیز زمانی رخ می‌دهد که نیروی بزرگ‌تر در تکیه‌گاه قرار داشته باشد. در این حالت عکس‌العمل $$ R _ 2 $$ باید در اولین قدم محاسبه شود. در این حالت عکس‌العمل $$ R _ 2 $$ برابر است با:
$$ \large \Sigma M _ { R 1 } = 0 $$
$$ \large 1 0 R _ 2 = 100 ( 8 ) $$
$$ R _ 2 = 80 \, \text{kN} $$
در نتیجه ماکزیمم مقدار نیروی برشی برابر است با:
$$ \large V _ { m a x } = 80 \, \text {kN} \,\, $$
مثال ۲
مطابق با شکل زیر تراکتوری به وزنِ $$ 3000 \ \ l b $$ را در نظر بگیرید که فاصله دو چرخ آن برابر با $$ 9 \ f t $$ است. در محل قرار‌گیری چرخ بزرگ‌تر وزنِ $$1800 \ lb$$ تحمل می‌شود. گشتاور و نیروی برشی ماکزیمم در هنگام عبور این تراکتور روی یک تیر طول $$14 \ ft$$ را بدست آورید.
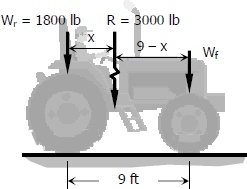
به‌منظور حل در ابتدا باید نیروی ناشی از وزن را محاسبه کنیم. بدین منظور داریم:
$$ \large R = W _ r + W _ f $$
$$ \large 3000 = 1800 + W _ f $$
$$ \large W _ f = 1200 \, \text{lb} $$
با فرض قرار داشتن نیروی معادل در فاصله $$ x $$ از لبه سمت چپ داریم:
$$ R _ x = 9 W _ f $$
$$\large 3000 x = 9 ( 1200 ) $$
$$ \Rightarrow x = 3.6 \ \ ft $$
بنابراین فاصله نیروی معادل تا چرخ سمت راست نیز برابر است با:
$$ \large 9 - x = 5.4 \, \text{ft}$$
با توجه به این‌که وسط تیر بین دو نیروی معادل ($$ W _ r $$) و بار ناشی از چرخ ($$ R $$) بزرگ‌تر قرار گرفته، می‌توان گفت بار ناشی از چرخ کوچک‌تر روی تیر قرار نگرفته است. در این حالت فقط بار ناشی از چرخ بزرگ‌تر، روی تیر نیز اعمال می‌شود.
ماکزیمم گشتاور در این شرایط زمانی رخ می‌دهد که بار چرخ بزرگ‌تر دقیقا در وسط تیر قرار گرفته باشد. در این حالت عکس‌العمل‌ها برابرند با:
$$ \large R _ 1 = R _ 2 = \frac { 1 } { 2 } ( 1800 ) $$
$$ \large R _ 1 = 900 \, \text{lb} $$
این حالت از بارگذاری نیز در شکل زیر ارائه شده.
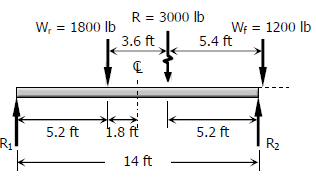
در این حالت ماکزیمم میزان گشتاور زیر نیروی $$ W _ r $$ برابر می‌شود با:
$$ \large M _ { m a x } = 7 R _ 1 $$
$$ \large M _ { m a x } = 7 (900) = 6300 \ lb.ft $$
محل نیرو‌ها در حالتِ ماکزیمم میزان بارگذاری نشان داده شده‌اند.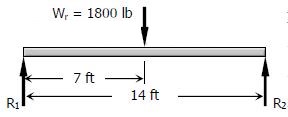
برای بدست آوردنِ میزان گشتاور در نتیجه وارد شدن نیروی $$ W _ f $$ در اولین قدم باید عکس‌العمل‌های تیکه‌گاه را بدست آوریم. عکس‌العملِ $$ R _ 2 $$ برابر است با:
$$ \sum M _ { R 1 } = 0 $$
$$ 14 R _ 2 = 4.3 R \Rightarrow R _ 2 = 921.43 \ lb $$
بنابراین گشتاور ماکزیمم ناشی از نیروی $$ W _ f $$ برابر می‌شود با:
$$ M _ { m a x } = 4 . 3 R _ 2 $$
$$ \Rightarrow M _ { m a x } = 4 . 3 × 921.43 = 3962 . 1 $$
در نتیجه با مقایسه حالت‌های فوق، ماکزیمم میزان گشتاور برابر می‌شود با:
$$ m a x \ \ {(6300,3962.1)} = 6300 $$
ماکزیمم میزان نیروی برشی نیز هنگامی رخ می‌دهد که بار ناشی از چرخ بزرگ‌تر روی تکیه‌گاه قرار داشته باشد. در این حالت در ابتدا باید عکس‌العمل تکیه‌گاه را در نقطه ۱ بدست آورد.
$$ Σ M R _ 2 = 0 \\
14 R _ 1=10 . 4 R \\
14 R _ 1 = 10.4 ( 3000 ) \\
R _ 1 = 2 2 2 8 .57 l b $$
در نتیجه بیشترین مقدار ممکن برای نیروی برشی نیز برابر می‌شود با:
$$ \large V _ { max } = 2228.57 \, \text{lb} \,\,$$
در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی عمران و مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- تحلیل پیچش در لوله های جدار نازک – آموزش جامع
- تعیین مولفه های تنش و کرنش در حالت برش خالص – آموزش جامع
^^
