فرادرس
انواع مختلف کنترل کننده صنعتی — راهنمای جامع
در حالت کلی می‌توان گفت که یک کنترل کننده صنعتی واحدی است که در یک سیستم کنترلی حضور دارد و مسئول تولید سیگنال‌های کنترلی به منظور کاهش انحراف «مقدار واقعی» (Actual Value) از «مقدار مطلوب» (Desired Value) شناخته می‌شود. در واقع کنترل کننده تلاش می‌کند که اختلاف بین سیگنال واقعی و سیگنال مطلوب در حالت ایده‌آل به صفر برسد، البته در کاربردهای عملی این مقدار که به آن خطا می‌گویند، به صفر نمی‌رسد، بلکه تلاش می‌شود به کمترین حد ممکن کاهش پیدا کند. بنابراین کنترل کننده در سیستم‌های صنعتی باید عملکرد سیستم را کنترل کند تا دقیق‌ترین پاسخ یا خروجی ممکن از سیستم دریافت شود. در این مطلب قصد داریم با انواع مختلف کنترل کننده صنعتی آشنا شویم و هر کدام را به اختصار بررسی کنیم.
کنترل کننده صنعتی چیست؟
همان طور که گفتیم، کنترل کننده در یک سیستم صنعتی مسئول تولید سیگنال کنترلی است. روش تولید سیگنال کنترلی توسط کنترل کننده الگوریتم‌های مختلفی دارد و به آن «عمل کنترلی» (Control Action) یا الگوریتم کنترل می‌گویند.
در تصویر زیر بلوک دیاگرام یک کنترل کننده صنعتی را نشان می‌دهد.
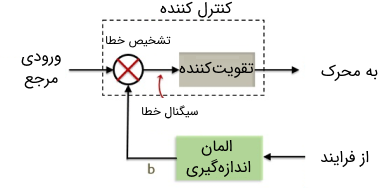
در تصویر فوق نیز دیده می‌شود که مقدار انحراف سیگنال به دست آمده نسبت به سیگنال مرجع برابر با سیگنال خطا است و باید توسط کنترل کننده این مقدار خطا را «جبران» (Compensate) کرد تا در خروجی سیستم، یک سیگنال مطلوب به دست آید. در مقالات قبلی فرادرس به این موضوع اشاره کردیم که کنترل کننده می‌تواند سیستم را برای تولید مقادیر مختلف خروجی مدیریت کند، پس به عبارت دیگر در یک سیستم کنترلی، کنترل کننده مدیریت مورد نیاز برای سیستم را فراهم می‌کند تا مقدار خروجی لازم تولید شود. در ادامه انواع مختلف کنترل کننده ها را بررسی می‌کنیم که در سیستم‌های صنعتی مورد استفاده قرار می‌گیرند.
انواع کنترل کننده صنعتی
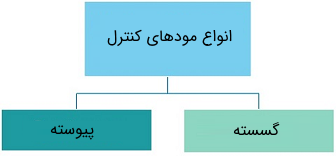
قبل از بررسی انواع مختلف کنترل کننده صنعتی، باید مودهای کنش کنترلی را بشناسیم؛ زیرا اساسا انواع مختلف کنترل کننده از مودهای مختلف کنش کنترلی سرچشمه می‌گیرد. دو نوع مود کنش کنترلی در نظر گرفته می‌شود که عبارتند از مود عملکرد پیوسته و مود عملکرد گسسته.
مود گسسته کنترل کننده صنعتی
مود عملکرد گسسته در کنترل کننده این امکان را فراهم می‌کند که کنترل کننده مقادیر گسسته را در خروجی ایجاد کند. در این مود کاری، خروجی متناسب با سیگنال تولید شده توسط کنترل کننده «تغییرات نرم» (Smooth Variation) ندارد و در عوض از یک مقدار به مقدار دیگری جهش می‌کند. بر اساس این مود کاری، کنترل کننده ها را می‌توان به دو نوع تقسیم کرد.
- کنترل کننده دو موقعیتی یا خاموش و روشن (On-Off / Two-Position Controllers)
- کنترل کننده چند موقعیتی (Multiposition Controllers)
مود پیوسته کنترل کننده صنعتی
این مود امکان تغییرات نرم خروجی کنترل شده را در سرتاسر بازه عملکرد ایجاد می‌کند. بنابراین خروجی سیستم کنترلی به صورت نرم متناسب با تمام یا بخشی از سیگنال خطا تغییر خواهد کرد. پس بر اساس ورودی اعمال شده به سیستم کنترل کننده در این مود را به انواع زیر تقسیم می‌کنند:
- کنترل کننده تناسبی (Proportional Controller)
- کنترل کننده انتگرال‌گیر (Integral Controller)
- کنترل کننده مشتق‌گیر (Derivative Controller)
حال می‌توانیم انواع مختلف کنترل کننده را بررسی کنیم.
کنترل کننده صنعتی دو موقعیتی
کنترل کننده صنعتی دو موقعیتی را با نام کنترل کننده خاموش و روشن نیز می‌شناسند. در این حالت، خروجی کنترل کننده بین دو مقدار مشخص نوسان می‌کند که این مقادیر معمولا مقادیر کمینه و بیشینه هستند. مقدار بیشینه برابر با ۱۰۰ درصد و مقدار کمینه برابر با ۰ درصد در نظر گرفته می‌شوند. این کنترل کننده ساده‌ترین و متداول‌ترین نوع کنترل کننده در صنعت محسوب می‌شود. در کنترل کننده خاموش و روشن، خروجی متناسب با سیگنال خطای «محرک» (Actuating)، بین مقدار کمینه و بیشینه نوسان می‌کند.
در واقع، زمانی که مقدار سیگنال خطای محرک به بالاتر از یک مقدار بحرانی از پیش تعیین شده برسد، خروجی نیز از مقدار کمینه به مقدار بیشینه تغییر خواهد یافت. به طریق مشابه، زمانی که سیگنال خطا به زیر مقدار بحرانی کاهش پیدا کند، خروجی نیز مجددا از مقدار بیشینه به مقدار کمینه کاهش پیدا می‌کند. فرض کنید $$ m $$ خروجی کنترل کننده، $$ e $$ سیگنال خطای محرک و $$ m _ 1 $$ و $$ m _ 2 $$ نیز به ترتیب نمایش دهنده مقادیر بیشینه و کمینه باشند. آن‌گاه می‌توانیم بنویسم:
$$ m = m _ 1 ( 100 ) \; \text {when } \; e > 0 $$
$$ m = m _ 2 ( 0 ) \; \text {when } \; e < 0 $$
در تصویر زیر بلوک دیاگرام یک کنترل کننده دو موقعیتی نشان داده شده است.
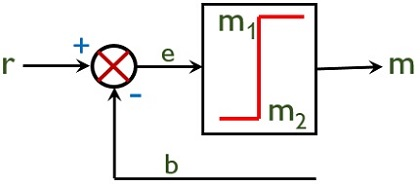
ذکر این نکته بسیار مهم است که در یک کنترل کننده دو موقعیتی، هر بار که سیگنال خطا کاهش یا افزایش می‌یابد، مقداری همپوشانی وجود خواهد داشت. این همپوشانی باعث می‌شود که گستره‌ای از خطا به وجود بیاید که به آن «ناحیه مرده» (Dead Zone) می‌گویند. به عنوان مثالی از سیستم‌هایی که از کنترل کننده دو موقعیتی یا خاموش و روشن استفاده می‌کنند، می‌توان به سیستم‌های گرمایشی، سیستم‌های کنترل سطح مایعات در مخازن آب و سیستم‌های تهویه هوا اشاره کرد.
کنترل کننده تناسبی
در این نوع از کنترل کننده‌ها، بین متغیر کنترل شده و سیگنال خطای محرک، یک رابطه خطی تناسبی وجود دارد. فرض کنید m برابر با خروجی کنترل کننده و e نشان دهنده سیگنال خطا باشد، در این صورت، برای کنترل کننده تناسبی، می‌توان رابطه ریاضی زیر را نوشت:
$$ m ( t ) = K _ p e ( t ) $$
در این رابطه، $$ K _ p $$ ثابت بهره تناسبی است و در واقع تعیین کننده رابطه بین خروجی کنترل شده و سیگنال خطا در نظر گرفته می‌شود. اگر بخواهیم رابطه فوق را بر اساس تبدیل لاپلاس بازنویسی کنیم، آن‌گاه معادله زیر به دست می‌آید:
$$ M ( S ) = K _ p E ( S ) $$
بنابراین ثابت بهره تناسبی به صورت زیر محاسبه می‌شود:
$$ K _ p = \frac { M ( S ) } { E ( S ) } $$
در نتیجه می‌توان گفت که در این حالت هر مقدار سیگنال خطا موجب تولید شدن یک مقدار خروجی کنترل کننده یکتا می‌شود. همان طور که گفتیم، یک تناسب خطی بین خروجی کنترل کننده و سیگنال خطا وجود دارد. البته توجه کنید که نباید خروجی کنترل کننده برابر با صفر شود؛ زیرا مقدار صفر برای سیگنال خطا منجر به ایجاد یک حالت «مکث» (Halt) در فرایند می‌شود. بنابراین برای حالتی که سیگنال خطا برابر با ۰ باشد، باید مقدار خروجی کنترل کننده به صورت زیر باشد:
$$ m ( t ) = K _ p e ( t ) + m _ 0 $$
در این رابطه $$ m _ 0 $$ برابر با خروجی کنترل شده در حالتی است که سیگنال خطا برابر با صفر باشد. این نوع کنترل کننده‌ها هم اجازه عمل کردن در مود مستقیم و هم در مود غیرمستقیم را می‌دهند. این ویژگی بدین دلیل است که مقدار خطا می‌تواند هم مثبت و هم منفی باشد که بستگی به مقدار تفاضل بین ورودی مرجع و سیگنال فیدبک دارد. در حالتی که همزمان با افزایش سیگنال ورودی به کنترل کننده، خروجی کنترل کننده نیز افزایش یابد، آن گاه کنترل کننده با نام «عمل کنترل مستقیم» (Direct Control Action) شناخته می‌شود. در حالی که اگر افزایش در سیگنال ورودی به کنترل کننده موجب کاهش در خروجی آن شود و یا کاهش در ورودی کنترل کننده موجب افزایش خروجی کنترل کننده شود، آن‌گاه کنترل کننده به عنوان «عمل معکوس» (Reverse Action) شناخته می‌شود.
کنترل کننده انتگرال‌گیر
یک کنترل کننده با نوعی عمل کنترلی که در آن نرخ تغییرات خروجی متناسب با سیگنال خطای محرک باشد را کنترل کننده انتگرال‌گیر می‌گویند. رابطه بین ورودی و خروجی یک کنترل کننده نوع انتگرال‌گیر را می‌توان با رابطه ریاضی زیر نشان داد:
$$ \frac { d } { d t } m ( t ) = K _ i e ( t ) $$
در این رابطه، پارامتر $$ K _ i $$ نشان دهنده مقداری ثابت است. رابطه فوق را می‌توان به صورت زیر نیز بازنویسی کرد:
$$ m ( t ) = K _ i \int e ( t ) + m _ 0 $$
پارامتر جدید $$ m _ 0 $$ که در رابطه به وجود می‌آید، نشان دهنده خروجی کنترل کننده در $$ t = 0 $$ است. در مورد کنترل کننده انتگرال‌گیر، نرخ تغییرات خروجی کنترل کننده به ثابت زمانی انتگرال‌گیری وابسته است تا سیگنال خطای زمانی صفر شود. بنابراین می‌توان گفت که در حالت کلی کنترل کننده نوع انتگرال‌گیر نسبت به کنترل کننده نوع تناسبی کندتر عمل می‌کند. به عبارت دیگر، در یک کنترل کننده نوع انتگرال‌گیر به منظور تولید یک خروجی مناسب، به زمان نسبتا بیشتری برای صفر شدن سیگنال خطای زمانی نیاز داریم.
کنترل کننده مشتق‌گیر
یک نوع دیگر از کنترل کننده‌ها وجود دارند که به آن‌ها کنترل کننده‌های مشتق‌گیر می‌گویند. در یک کنترل کننده نوع مشتق‌گیر، خروجی کنترل کننده به نرخ تغییرات سیگنال خطا بستگی دارد. در کاربردهای عملی، می‌توان گفت که خطا تابعی از زمان است و در هر لحظه از زمان می‌تواند برابر با صفر شود. البته به هیچ وجه ضرورت ندارد که بعد از آن لحظه از زمان همچنان صفر باقی بماند. بنابراین ضروری است که یک عمل کنترلی انجام گیرد که نرخ تغییرات سیگنال خطا را مشخص کند. گاهی اوقات به آن «مود عمل نرخ» (Rate Action Mode) نیز می‌گویند. کنترل کننده‌های نوع مشتق‌گیر را می‌توان به رابطه ریاضی زیر توصیف کرد:
$$ m ( t ) = K _ d \frac { d } { d t } e ( t ) $$
در این رابطه، $$ K _ d $$ نشان دهنده بهره ثابت مشتق‌گیر است که میزان تغییرات در خروجی کنترل کننده را به ازای هر نرخ تغییرات سیگنال خطای محرک (بر ثانیه) نشان می‌دهد. رابطه بین ورودی و خروجی یک کنترل کننده نوع مشتق‌گیر را می‌توان در فرم لاپلاس به صورت زیر نشان داد:
$$ M ( S ) = K _ d S . E ( S ) $$
همچنین این رابطه را می‌توان به صورت زیر بازنویسی کرد:
$$ \frac { M ( S ) } { E ( S ) } = S K _ d $$
بر اساس این روابط می‌توان گفت که به ازای هر میزان نرخ تغییرات سیگنال خطا، یک مقدار متفاوتی برای خروجی کنترل کننده به دست می‌آید. این خاصیت به عنوان یک مزیت برای سیستم شناخته می‌شود؛ زیرا هر بار خروجی با تغییرات سیگنال خطا تغییر می‌کند. بنابراین کنترل کننده قبل از اینکه خطا به یک مقدار بسیار بزرگ نزدیک شود، یک سیگنال کنترلی مناسب را ایجاد می‌کند و خروجی را تصحیح می‌کند.
نکته مهمی که در مورد این کنترل کننده‌ها وجود دارد این است که معمولا در کاربردهای عملی از آن‌ها به تنهایی استفاده نمی‌شود، بلکه کنترل کننده اصلی ترکیبات مختلفی از انواع تناسبی، مشتق‌گیر و انتگرال‌گیر به شمار می‌آید. این ترکیبات به صورت زیر هستند.
کنترل کننده‌های تناسبی انتگرال‌گیر
کنترل کننده‌های تناسبی انتگرال‌گیر (Proportional Integral Controller) یا به اختصار PI، از طریق ترکیب دو عمل کنترلی تناسبی و انتگرالی به وجود می‌آیند. کنترل کننده‌های نوع PI را می‌توان با استفاده از عبارت ریاضی زیر نمایش داد:
$$ m ( t ) = K _ p e ( t ) + K _ p K _ i \int _ { 0 } ^ { t } d t + m ( 0 ) $$
در این رابطه، $$ m ( 0 ) $$ نشان دهنده مقدار خروجی اولیه در زمان $$ t = 0 $$ است.
کنترل کننده‌های تناسبی مشتق‌گیر
کنترل کننده‌های تناسبی مشتق‌گیر (Proportional Derivative Controller) یا PD زمانی به وجود می‌آیند که عمل کنترلی تناسبی به صورت سریال با عمل کنترلی مشتقی ترکیب شود. کنترل کنده‌های تناسبی مشتق‌گیر را می‌توان با رابطه ریاضی زیر نشان داد:
$$ m ( t ) = K _ p e ( t ) + K _ p T _ d \frac { d } { d t } e ( t ) $$
کنترل کننده‌های تناسبی مشتق‌گیر انتگرال‌گیر
کنترل کننده‌های تناسبی مشتق‌گیر انتگرال‌گیر (Proportional Integral Derivative Controller) که به اختصار به آن‌ها کنترل کننده PID می‌گویند، نوع دیگری از کنترل کننده‌های ترکیبی هستند که هر سه نوع کنترل کننده تناسبی، مشتق‌گیر و نیز انتگرال‌گیر را با هم ترکیب می‌کند. کنترل کننده PID را با رابطه زیر نشان می‌دهند:
$$ m ( t ) = K _ p e ( t ) + K _ p T _ d \frac { d } { d t } e ( t ) + K _ p \frac { 1 } { T _ i } \int _ { 0 } ^ { t } e ( t ) d t $$
اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس مهندسی کنترل
- آموزش سیستم های کنترل خطی
- مجموعه آموزش‌های مهندسی برق
- آموزش مدارهای الکتریکی ۱
- حاشیه فاز و حاشیه بهره — از صفر تا صد
- معیار پایداری نایکویست در سیستم کنترل — از صفر تا صد
- جبران ساز پیش فاز و پس فاز — از صفر تا صد
^^
