جبران ساز پیش فاز و پس فاز — از صفر تا صد
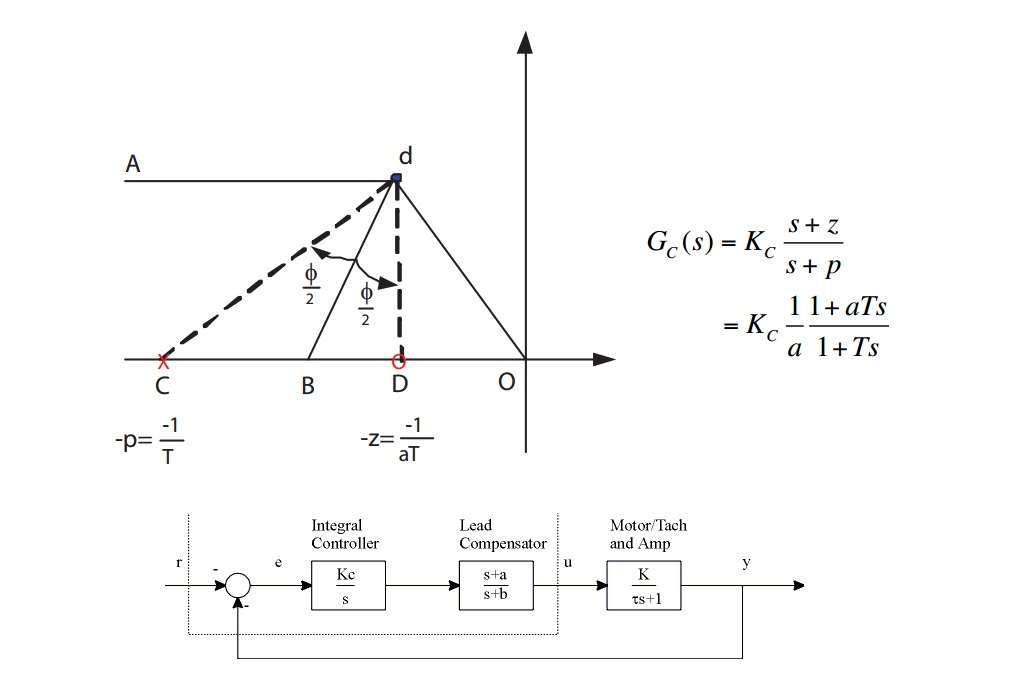
در مطالب قبلی مجله فرادرس به بررسی نحوه ترسیم نمودار مکان هندسی ریشهها پرداختیم. در این مطلب قصد داریم به بررسی جبران ساز پیش فاز (Lead Compensator) و جبران ساز پس فاز (Lag Compensator) بپردازیم. برای ترسیم مکان هندسی ریشهها قوانین متعددی وجود دارد. اما مهمترین این قواعد، نقاط شکست (Breakaway Points) روی محور حقیقی، محل تلاقی مجانبها (Origin of Asymptotes) و زاویه خروج از قطبهای حلقه باز و زاویه ورود به صفرهای حلقه باز هستند. در ادامه ابتدا به بررسی موضوع کنترلکننده PD با استفاده از جبران ساز دینامیک میپردازیم و سپس نحوه طراحی جبران ساز پیش فاز و پس فاز را بیان میکنیم.
کنترلکننده PD با استفاده از جبران ساز دینامیک
با استفاده از ترسیم مکان هندسی ریشهها (Root Locus) میتوان تاثیر افزودن کنترل D را به یک کنترلکننده نشان داد. افزودن یک صفر در سمت چپ صفحه باعث میشود که قطبهای حلقه بسته به سمت چپ صفحه حرکت داده شوند و بنابراین به پایداری سیستم کمک میکند.
البته در حال حاضر میدانیم که کنترلکننده PD به صورت فیزیکی قابل تحقق نیست؛ زیرا یک سیستم غیرعلّی است. اما جبران سازهای دینامیک نسبت به کنترل P با کنترلکنندهها به صورت عمومیتر برخورد میکنند. جبران ساز دینامیک توسط سیستمهای علی به فرم زیر قابل پیادهسازی است:
$$ \begin{align*}
\dot{z} &= Az + Be \\
u &= Cz + De.
\end{align*} $$
در شکل زیر نمایش بلوک دیاگرامی جبران ساز دینامیک را مشاهده میکنید.
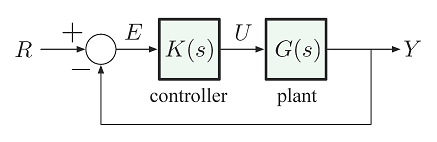
به دلیل این که سیستم علی است، میتوان آن را توسط یک تابع انتقال مناسب توصیف کرد. میتوانیم المان کنترلکننده D یعنی $$ K_{\rm D}s $$ را به صورت زیر تقریب بزنیم:
$$ \begin{align*}
K_{\rm D}\frac{ps}{s+p} \longrightarrow K_{\rm D}s \text{ as } p \to \infty.
\end{align*} $$
در تقریب بالا، P قطب کنترلکننده محسوب میشود. در این کنترلکننده میتوانیم $$ K_{\rm P} + K_{\rm D}s $$ را توسط $$ \begin{align*} K(s) = K_{\rm P} + K_{\rm D}\frac{ps}{s+p}
\end{align*} $$ جایگزین کنیم. بنابراین معادله مشخصه به صورت زیر است:
$$ 1 + \left( K_{\rm P} + K_{\rm D}\dfrac{ps}{s+p} \right) G(s) = 0. $$
با تطبیق این معادله و مکان هندسی ریشهها، میتوانیم معادله کنترلکننده PD را به صورت زیر بنویسیم:
$$ \begin{align*}
K_{\rm P} + K_{\rm D}\frac{ps}{s+p} &= \frac{(K_{\rm P} + pK_{\rm D})s + pK_{\rm P}}{s+p} \\
&= (K_{\rm P} + pK_{\rm D}) \cdot \frac{s + \frac{pK_{\rm P}}{K_{\rm P}+p K_{\rm D}}}{s+p}.
\end{align*} $$
بنابراین کنترلکننده PD در فرم $$ K \cdot \frac{s+z}{s+p} $$ نوشته میشود. در این فرمول داریم:
- پارامتر $$ K = K_{\rm P} + pK_{\rm D} $$ ترکیب بهره کنترل P، بهره کنترل D و P است.
- کنترلکننده دارای صفر حلقه باز در $$ -z = -\frac{pK_{\rm P}}{K} $$ است.
فرم انتگرالگیر دوگانه را به یاد بیاورید. در تصویر زیر جبران ساز دینامیک برای سیستم انتگرالگیر دوگانه پیادهسازی شده است.
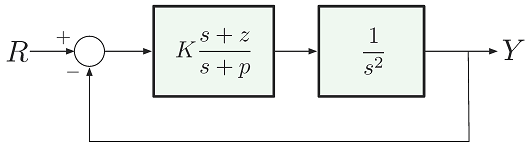
معادله مشخصه در این جبران ساز دینامیک به صورت زیر نوشته میشود:
$$ 1 + K \cdot \underbrace{\dfrac{s+z}{s+p} \cdot \dfrac{1}{s^2}}_{:=L(s)} = 1 + KL(s) = 0. $$
توجه کنید که $$ L(s) $$ تابع انتقال حلقه باز سیستم نیست، این تابع با استفاده از بهره مسیر مستقیم تحت تاثیر کنترلکننده روی پلنت به دست میآید.
جبران ساز پیش فاز و پس فاز
در این قسمت میخواهیم جزئیات بیشتری را درباره استفاده از جبران ساز دینامیک برای پیادهسازی تقریبی کنترلکننده PD و PI بررسی کنیم.
بر اساس دیاگرام جبران ساز دینامیک برای انتگرالگیر دوگانه که در قسمت قبل نمایش داده شد، معادله مشخصه متناظر با آن را میتوان به صورت زیر نوشت:
$$ \large
1 + K \cdot \underbrace { \dfrac { s + z } { s + p } \cdot \dfrac { 1 } { s ^ 2 } } _ { : = L ( s ) } = 1 + K L ( s ) = 0 . \; \; \; \; \; \; \; \; ( 1 ) $$
در این سیستم، کنترلکننده به فرم زیر است:
$$ \large K \frac { s + z } { s + p } $$
که در آن، پارامترهای مثبتِ $$ K $$، $$ z $$ و $$ p $$ پارامترهای طراحی هستند. کنترلکننده بالا یک جبران ساز پیش فاز یا پس فاز است. برای این کنترلکننده دو حالت زیر امکانپذیر است:
- یک جبران ساز پیش فاز است، اگر $$ z < p $$.
- یک جبران ساز پس فاز است، اگر $$ z > p $$.
اما نامگذاری جبران ساز پس فاز و جبران ساز پیش فاز به چه دلیل است؟ در واقع، با در نظر گرفتن $$ s = j\omega $$ در پاسخ فرکانسی، داریم:
$$ \large \begin {align*}
\angle \frac { j \omega + z } { j \omega + p } & = \angle ( z + j \omega ) - \angle ( p + j \omega ) \\
& = \psi - \phi .
\end{align*} \; \; \; \; \; \; \; \; (2) $$
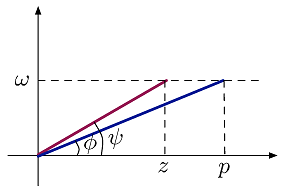
با توجه به شکل و معادله بالا میتوان نوشت:
- اگر $$ z < p $$ باشد، آنگاه $$ \psi - \phi > 0 $$ است و تقدم یا پیشی فاز داریم.
- اگر $$ z > p $$ باشد، آنگاه $$ \psi - \phi < 0 $$ است و تأخر یا پسی فاز داریم.
اعمال جبران ساز پیش فاز به انتگرالگیر دوگانه
همانگونه که در بلوک دیاگرام جبران ساز دینامیکی نشان داده شد، یک جبران ساز دینامیکی (تقریبی از کنترل PD) به صورت زیر به انتگرالگیر دوگانه اعمال شده است:
$$ \large K \dfrac { s + z } { s + p } \; \; \; \; \; \; \; \; (3) $$
که در آن، $$ K = K_{\rm P} + pK_{\rm D} $$ و $$ z = \frac { p K _ { \rm P } } { K _ { \rm P } + p K _ { \rm D } } $$ است. توجه کنید که اگر $$ p \to \infty $$، آنگاه $$ z \to
\frac{K_{\rm P}}{K_{\rm D}} $$ میل میکند که یک ثابت است.
بنابراین، جبران ساز دینامیکی مربوط به تقریب کنترل PD معادله (۳) یک جبران ساز پیش فاز است.
برای سادگی، فرض میکنیم $$ K_{\rm P} = K_{\rm D} $$ باشد. در نتیجه، خواهیم داشت:
$$ \large \begin {align*}
K & = K _ { \rm P } + p K _ { \rm D } = ( 1 + p ) K _ { \rm D } , \\
z & = \frac { p K _ { \rm P } } { K _ { \rm P } + p K _ { \rm D } } \\
& = \frac { p K _ { \rm D } } { ( 1 + p ) K _ { \rm D } } \\
& = \frac { p } { 1 + p } \\
& \to 1 , \text { as } p \to \infty .
\end {align*} $$
از آنجایی که میتوانیم $$ p $$ و $$ z $$ را مستقیماً انتخاب کنیم، فرض میکنیم $$ z = 1 $$ و $$ p $$ مقداری بزرگ باشد. بنابراین، انتظار داریم کنترلکننده معادله (۳) مشابه کنترل PD باشد.
اکنون میخواهیم چند مقدار عددی برای $$ p $$ با در نظر گرفتن $$ z = 1 $$ آزمایش کنیم. تابع تبدیل حلقه باز معادل $$ L ( s ) $$ در معادله (۱) به صورت زیر است:
$$ \large \begin {align*}
L ( s ) & = \frac { s + z } { s + p } \cdot \frac { 1 } { s ^ 2 } \\
& = \frac { s + 1 } {s ^ 2 ( s +p ) } .
\end {align*} $$
با قرار دادن $$ p = 10 $$، مکان ریشه $$L ( s) $$ به صورت زیر خواهد بود.
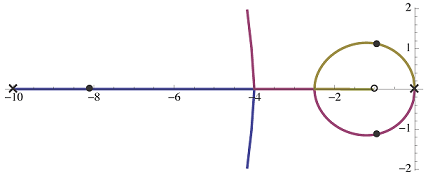
مطابق شکل بالا، مکان هندسی ریشهها شبیه مکان هندسی کنترل PD است. البته قطب در $$ s = -10 $$ سبب شده مکان هندسی در نیمصفحه سمت چپ متفاوت از مکان هندسی کنترل PD باشد. همان طور که از شکل مکان هندسی فوق مشخص است، طراحی جبران ساز پیش فاز مطلوب است و میرایی خوبی دارد.
اما آیا میتوانیم از هر مقداری برای $$ p $$ استفاده کنیم؟ در مرحله قبل از $$ p = 10 $$ استفاده کردیم و دیدیم که با بزرگ بودن $$ p $$ به کنترل PD بسیار نزدیک هستیم. اکنون مقدار $$p = 5 $$ را در نظر میگیریم. مکان هندسی ریشههای $$ L(s) = \frac{s+1}{s^2 (s+p)} $$ برای $$ p = 5 $$ در زیر نشان داده شده است.
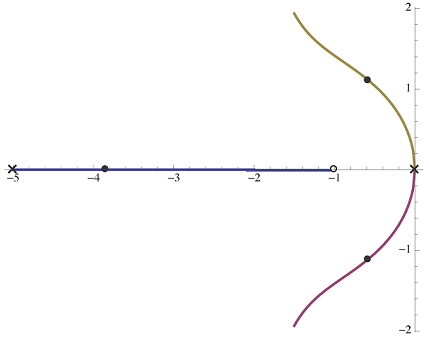
برای مقدار $$ p = 5 $$، نمودار مکان ریشه به صورت شکل بالا خواهد بود و همان طور که میبینیم تفاوت زیادی با حالت $$ p = 10 $$ دارد. میرایی در این حالت به خوبی حالت $$ p = 10 $$ نیست. اگر مقادیر مختلف بین $$ p = 5 $$ و $$ p = 10 $$ را بررسی کنیم، خواهیم دید که $$ p = 9 $$ انتخاب مناسبی است. نمودار مکان ریشههای $$ L(s) = \frac{s+1}{s^2 (s+p)} $$ برای $$ p = 9 $$ در تصویر زیر نشان داده شده است.
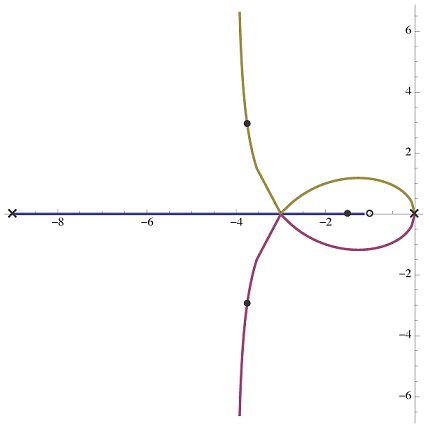
همان طور که میبینم، وقتی $$ p =9 $$ باشد، شاخههای مکان هندسی در نقطهای روی محور حقیقی به یکدیگر میرسند یا از هم جدا میشوند.
به طور خلاصه، در این روش سعی و خطا میتوان گفت:
- برای $$ p $$ بزرگ، میتوان نشان داد که نمودار مکان هندسی ریشهها میرایی مناسبی دارد، اما حذف نویز آن مناسب نیست که بسیار شبیه به کنترل PD است. در این حالت، شاخههای مکان ابتدا روی محور حقیقی به یکدیگر میرسند و سپس جدا میشوند.
- برای $$ p $$ کوچک، میتوان نشان داد که حذف نویز بهتر از حالت $$ p $$ بزرگ است. اما از آنجایی که $$ p $$ کوچک است، شباهت زیادی با کنترل PD ندارد. اما نمودار مکان هندسی در حالت کلی به محور $$ j \omega $$ نزدیک است که میرایی مناسبی ندارد. برای مقادیر کوچک $$ p $$، نقطه ورود و تلاقی وجود ندارد.
- برای مقدار $$ p $$ بین دو حالت قبلی، میتوان مکان هندسی ریشهها را رسم کرد و نشان داد که در این حالت نقاط تلاقی ورود و خروج یکی هستند.
طراحی جبران ساز پیش فاز
گفتیم که با بهرهگیری از یک جبران ساز پیش فاز، تابع تبدیل زیر را خواهیم داشت:
$$ \large K L ( s ) = K \frac { s + z } { s+ p } \cdot G _ p ( s ) , $$
که پارامتر صفر جبران ساز پیش فاز $$ z $$ و پارامتر قطب جبران ساز پیش فاز $$ p $$ در رابطه $$ z < p $$ صدق میکنند.
در مثال کنترل انتگرالگیر دوگانه با تابع تبدیل $$ G_p(s) = \frac{1}{s^2} $$، برای کنترل تقریبی PD مقدار $$ z = 1 $$ را فرض کردیم. پس از آن، $$ p > 1 $$ را به عنوان پارامتر طراحی در نظر گرفتیم. $$ K $$ پارامتر بهره متغیر در مکان هندسی ریشهها بود.
میتوانیم $$ p $$ را به عنوان پارامتر معلوم در نظر بگیریم (به دلیل الزامات حذف نویز) و $$ z $$ مناسب را پیدا کنیم. حال این پرسش پیش میآید که آیا روند نظاممندی برای طراحی جبران ساز پیش فاز وجود دارد؟ بخش بعدی، پاسخ این پرسش است.
جایابی قطب با استفاده از مکان ریشهها
باز هم مثال انتگرالگیر دوگانه را با جبران ساز پیش فاز در نظر میگیریم:
$$ \large K L ( s ) = K \frac { s + z } { s + p } \cdot \frac { 1 } { s ^ 2 } . \; \; \; \; \; \; \; \; (4) $$
با فرض داشتن $$ p $$ و قطب حلقه بسته مطلوب $$ s $$، میخواهیم (در صورت امکان) مقدار $$ z $$ را تعیین کنیم. برای این کار، از شرط فاز $$ \angle L(s) = 180^{\circ} $$ برای $$ L (s) $$ در معادله (۴) استفاده میکنیم.
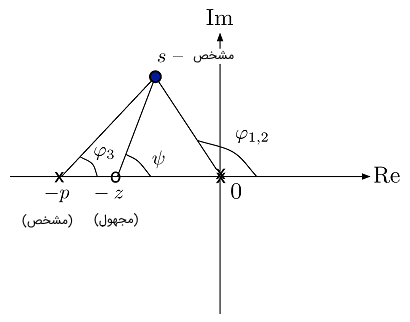
بنابراین، داریم:
$$ \large \begin {align*}
\angle L ( s ) & = \underbrace { \psi } _ { \text {angle from} \atop \text {$s$ to zero}} - \sum _ i \underbrace { \varphi _ i } _ { \text {angles from} \atop\text {$s$ to poles}} \\
& = \angle ( s + z ) - \angle ( s + p ) - 2 \angle ( s - 0 ) \\
& \\
& = 1 8 0 ^ \circ . \\
\implies \psi & = 1 8 0 ^ \circ + \sum _ i \varphi _ i \\
& = 1 8 0 ^ \circ + \angle ( s + p ) + 2 \angle s .
\end {align*} $$
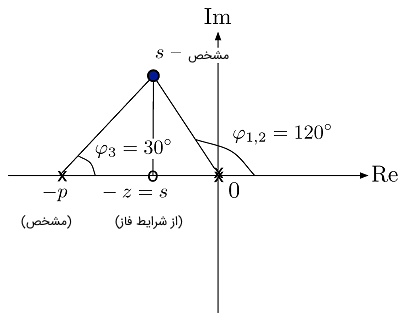
برای مثال، با فرض $$ \varphi_1 = \varphi_2 = 120^\circ $$ و $$ \varphi_3 = 30^\circ $$، داریم:
$$ \large \begin {align*}
\psi & = 1 8 0 ^ \circ + \sum _ i \varphi _ i \\
& = 1 8 0 ^ \circ + 1 2 0 ^ \circ + 1 2 0 ^ \circ + 3 0 ^ \circ \\
& = 4 5 0 ^ \circ \\
& = 9 0 ^ \circ \bmod 3 6 0 ^ \circ
\end {align*} $$
بنابراین، باید داشته باشیم:
$$ z = -{\rm Re}(s) $$
طراحی کنترل با استفاده از مکان ریشهها
تابع تبدیل ناپایدار $$ G _ p ( s ) = \dfrac { 1 } { s - 1 } $$ را در نظر بگیرید. میخواهیم آن را با ردیابی یک مرجع ثابت پایدار کنیم. میدانیم که برای بهبود ردیابی حالت ماندگار میتوان از کنترلکننده PI استفاده کرد.
در تصویر زیر بلوک دیاگرام کنترلکننده PI برای سیستم ناپایدار $$ G_p(s) = \dfrac{1}{s-1} $$ را مشاهده میکنید.
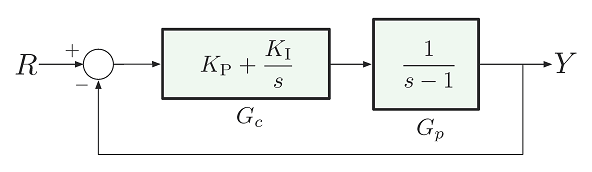
قطبهای حلقه بسته برای این سیستم توسط معادله مشخصه زیر تعیین میشوند:
$$ \large 1 + \underbrace{\left(K_{\rm P} + \frac{K_{\rm I}}{s}\right)}_{G_c(s)} \underbrace{\left(\frac{1}{s-1}\right)}_{G_p(s)} = 0. $$
برای استفاده از روش مکان ریشهها، معادله فوق را به فرم $$ 1 + KL(s) = 0 $$ تبدیل کردیم که در آن داریم:
$$ L(s) = \dfrac{b(s)}{a(s)} = \dfrac{s^m + b_1 s^{m-1} + \cdots}{s^n +
a_1 s^{n-1} + \cdots} $$
مقدار فوق باید به صورت مناسب و منطقی انتخاب شود. $$ K = K_{\rm P} $$ را به عنوان پارامتر متغیر انتخاب میکنیم. همچنین با فرض $$ K_{\rm I}/K_{\rm P} $$ برابر با مقدار ثابتی مانند یک، معادله مشخصه را بازنویسی میکنیم تا $$ L(s) $$ را در سیستم حلقه باز به دست آوریم:
$$ \begin{align*}
1 + \left(K_{\rm P} + \frac{K_{\rm I}}{s}\right)\frac{1}{s-1} &= 1 + \frac{K_{\rm P}s + K_{\rm I}}{s} \frac{1}{s-1} \\
& = 1 + K_{\rm P} \frac{s + K_{\rm I}/K_{\rm P}}{s(s-1)}\\
& = 1 + K \underbrace{\frac{s + 1}{s(s-1)}}_{:=L(s)}.
\end{align*} $$
حال با داشتن $$ L(s) = \frac{s + 1}{s(s-1)} $$، میتوان مکان هندسی ریشهها را برای $$ 1 + KL(s) $$ ترسیم کنیم.
- بر اساس قاعده اول، میتوان دانست که ۲ شاخه در مکان هندسی وجود دارد.
- بر اساس قاعده دوم، شاخههای مکان هندسی از $$ p_1 = 0 $$ و $$ p_2 = 1 $$ شروع میشوند. همچنین باید توجه کرد که $$ p_2 = 1 $$ در سمت راست صفحه قرار دارد.
- بر اساس قاعده سوم، شاخههای مکان هندسی در $$ z_1 = -1 $$ و $$ \pm \infty $$ به پایان می رسند.
- بر اساس قاعده چهارم، مکان هندسی در دو بازه $$ [0,1] $$ و $$ (-\infty,-1] $$ روی محور حقیقی قرار دارند.
- بر اسای قاعده پنجم، تنها یک مجانب با زاویه 180 درجه در نمودار مکان هندسی وجود دارد.
- بر اساس قاعده ششم، نقاط عبور از محور $$ jω $$ به صورت زیر به دست میآیند:
$$ \large \begin{align*}
a(s) + Kb(s) &= 0 \\
\implies s(s-1) + K(s+1) &= 0 \\
s^2 + (K-1)s + K &= 0 \\
\implies \hspace{1cm} K_{\rm critical} = 1,\, \omega_0 &= 1.
\end{align*}\;\;\;\;\;\;\;(5) $$
مکان هندسی ریشهها در تصویر زیر نشان داده شده است.

با توجه به مکان هندسی ریشهها، میتوان نتیجه گرفت که:
- برای اینکه قطبهای سیستم حلقه بسته در سمت چپ صفحه قرار گیرند و سیستم پایدار باشد، باید به سمت چپ معادله شماره (۵) بر اساس معیار راث هرویتز $$ K > 1 $$ را اعمال کنیم.
- برای $$ k $$های بسیار بزرگ، سیستم به صورت کامل میرا میشود. به عبارت دیگر، در قطبهای حقیقی منفی $$ \zeta > 1 $$ است.
- ردیابی حالت ماندگار یک مرجع ثابت، ایدهآل است. در واقع:
$$ \begin{align*}
\frac{E}{R}(s) &= \frac{1}{1+G_cG_p} \\
&= \frac{s(s-1)}{s(s-1) + K(s+1)}. \\
\end{align*} $$
- تا زمانی که $$ K > 1 $$ باشد، پایداری سیستم تضمین شده است. بنابراین، بر اساس قضیه مقدار نهایی، بهره DC در $$ \frac{E}{R}(s) $$ برابر با صفر خواهد بود.
اما $$ \frac {1} {s} $$ یک المان پایدار نیست، بنابراین میخواهیم که یک کنترلکننده PI را با جبران ساز دینامیک تقریب بزنیم. این کار بسیار شبیه به آنچه است که در مورد کنترلکننده PD انجام دادیم.
تقریب PI با جبران سازی دینامیکی
یک کنترلکننده PI به فرم عمومی $$ K_{\rm P} + \frac{K_{\rm I}}s $$ را میتوان با یک جبران ساز پس فاز تقریب زد. با فرض $$ z = \frac{ K_{\rm I} }{ K_{\rm P} } $$، عبارت $$ K \frac{s+z}{s} $$ را با $$ K\frac{s+z}{s+p} $$ جایگزین میکنیم که در آن، $$ p < z $$ است.
این جایگزینی به یک جبران ساز یا کنترلکننده پس فاز میانجامد. در نتیجه، کنترلکننده پس فاز جبران سازی برای تقریب کنترل PI است.
سیستم ناپایدار $$ G_p(s) = \frac{1}{s-1} $$ را با جبران ساز پس فاز $$ G_c(s) = K \frac{s+z}{s+p} $$ و $$ p < z $$ در نظر بگیرید. انتظار میرود جبران ساز پس فاز از آنجایی که تقریبی از کنترل PI است، ردیابی کاملی داشته باشد.
برای تضمین پایداری حلقه بسته، تابع تبدیل زیر نباید قطبی در نیمصفحه سمت راست داشته باشد:
$$ \frac { E ( s ) } { R ( s ) } = \dfrac { 1 } { 1 + G _ c ( s ) G _ p ( s ) } . $$
از معادله مشخصه استفاده میکنیم:
$$ \large \begin {align*}
( s + p ) ( s - 1 ) + K ( s + z ) & = 0 \\
s ^ 2 + ( K + p - 1 ) s + K z - p & = 0
\end {align*} $$
برای پایداری حلقه بسته، باید روابط $$ K > 1-p $$ و $$ Kz > p $$ برقرار باشند.
با در نظر گرفتن پایداری حلقه بسته، از قضیه مقدار نهایی استفاده میکنیم:
$$ \large \begin {align*}
e ( \infty ) & = \frac { 1 } { 1 + G _ c ( s ) G _ p ( s ) } \Big | _ { s = 0 } \\
& = \frac { 1 } { 1 + K \frac { s + z } { ( s + p ) ( s - 1 ) } } \Big | _ { s = 0 } \\
& = \frac { 1 } { 1 - \frac { K z } { p } } .
\end{align*} \; \;\;\;\;\;\;\; (6)
$$
همانطور که میبینیم، خطای حالت ماندگار در معادله (۶) دقیقاً برابر با صفر نیست و اگر $$ \frac{Kz}{p} $$ بزرگ باشد، میتواند نزدیک صفر (و منفی) شود. جبران سازی پس فاز ردیابی کاملی ندارد و در واقع، نوع سیستم را تغییر نمیدهد. اما میتوانیم با استفاده از آن و تنظیم مناسب پارامترهای $$ K $$، $$ z $$ و $$p$$ ردیابی مناسبی انجام دهیم. از طرف دیگر، برخلاف کنترل PI، جبران سازی پس فاز، یک کنترلکننده پایدار را نتیجه خواهد داد.
تأثیر جبران سازی پس فاز بر مکان ریشهها
اکنون تابع تبدیل زیر را در حضور کنترل PI (که در آن $$ \frac{K_{\rm I}}{K_{\rm P}} = 1 $$ است.) برای سیستم ناپایدار $$ G_p (s) = \frac{1}{s - 1} $$ در نظر بگیرید:
$$ \large L ( s ) = \frac { s + 1 } { ( s + p ) ( s - 1 ) } $$
با انتخاب یک $$ p $$ کوچک، که بسیار نزدیک به صفر است، میتوانیم مکان ریشه را به طور دلخواه به مکان ریشه PI نزدیک کنیم (برای $$ K $$ به اندازه کافی بزرگ پایدار است). در واقع، $$ p = 0.1 $$ را در نظر میگیریم.
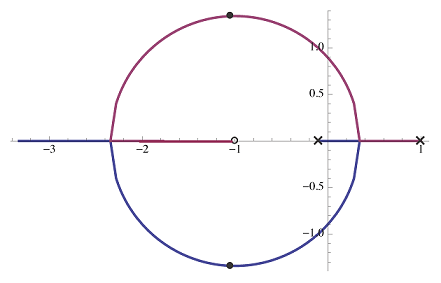
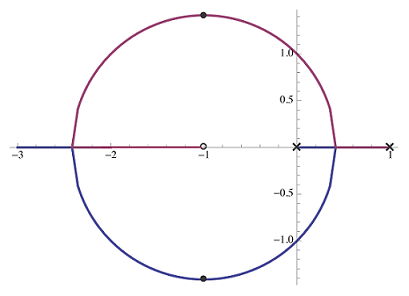
با توجه به شکلهای قبل، زمانی که کنترل PD را با یک جبران ساز پیش فاز $$ K \frac{s + z}{s + p} $$ با $$ p $$ بزرگ تقریب بزنیم، مکان ریشه تنها به بخشی از مکان هندسی اصلی شباهت دارد. زیرا تقریب $$ s \mapsto \frac{ps}{s + p} $$ با $$ p $$ بزرگ متفاوت از مکان اصلی با یک قطب اضافه است.
$$ \large s \mapsto \frac{ps}{s + p}, ~\, p \text{ large }$$
اما در اینجا، شکل مکان هندسی ریشه PI در برابر کنترل پس فاز، در مقایسه با مکان هندسی ریشه PD در برابر کنترل پیش فاز، تغییر کیفی دچار تغییر کیفی چندانی نخواهد شد؛ زیرا تعداد صفرها یا قطبهای اصلی را با تقریب تغییر ندادهایم.
$$ \large \frac{1}s \mapsto \frac{1}{s + p}, ~\, p \text{ small}. $$
مانند قبل، میتوانیم $$ \large z_{lag} $$ را با توجه به مکان قطبهای مطلوب برای یک $$ \large p_{\rm lag} $$ ثابت به دست آوریم (و بالعکس). فرایند انجام این کار، دقیقاً مشابه آنچه است که برای جبران ساز پیش فاز انجام دادیم.
پارامترها را به گونهای انتخاب میکنیم که در شرایط فاز صدق کنند، یعنی نقاط روی مکان ریشه باید همیشه به صورتی باشند که $$\angle L(s) = 180^\circ$$ برقرار باشد.
مثال
سیستم $$ G_p(s) $$ و کنترلکننده $$ G_c(s) $$ را به صورت زیر در نظر بگیرید:
$$ \large G _ p ( s ) = \dfrac { 1 } { s - 1 } , \qquad G _ c ( s ) = K \dfrac { s + z } { s + p } . $$
به ازای $$p = 2 $$، پارامترهای $$ K $$ و $$ z $$ را به صورتی محاسبه کنید که قطبها در $$ -2 \pm 3j $$ قرار گیرند.
حل:
چندجملهای مشخصه مطلوب به صورت زیر است:
$$ \large \begin {align*}
( s + 2 ) ^ 2 + 9 = s ^ 2 + 4 s + 1 3 .
\end {align*} $$
ضریب میرایی نیز برابر با $$ \zeta = \frac{2}{\sqrt{13}} \approx 0.555 $$ به دست میآید.
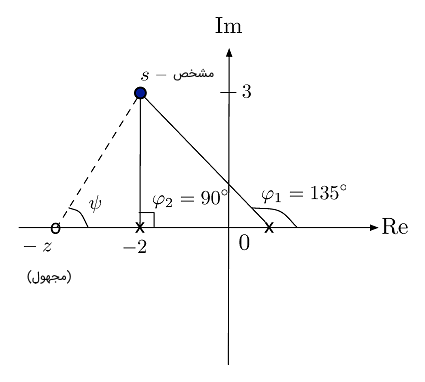
در نتیجه، باید داشته باشیم:
$$ \large \begin {align*}
\underbrace { \psi } _ { \text {angle from} \atop \text {$s$ to zero}} - \sum _ i \underbrace { \varphi _ i } _ { \text {angles from} \atop \text {$s$ to poles}} = 1 8 0 ^ \circ , & \\
\implies \psi = 1 8 0 ^ \circ + \sum _ i \varphi _ i & .
\end {align*} $$
بر اساس محل قطبها، باید $$ \varphi_1 = 135^\circ $$ و $$ \varphi_2 = 90^\circ $$ باشد. بنابراین، داریم:
$$ \large \begin {align*}
\psi & = 1 8 0 ^ \circ + \sum _ i \varphi _ i \\
& = 1 8 0 ^ \circ + 1 3 5 ^ \circ + 9 0 ^ \circ \\
& = 4 0 5 ^ \circ \\
& = 4 5 ^ \circ \bmod 3 6 0 ^ \circ .
\end {align*} $$
صفر $$ -z = -5 $$ را مطابق شکل زیر انتخاب میکنیم.
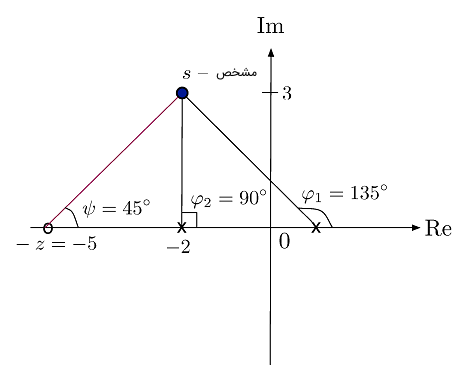
با $$ z = 5 $$، چندجملهای مشخصه بر اساس $$ G_p(s) = \frac{1}{s - 1} $$ و $$ G_c(s) = K \frac{s + z}{s + p} $$ به صورت زیر خواهد بود:
$$ \large \begin {align*}
( s - 1 ) ( s + p ) & + K ( s + z ) \\
( s - 1 ) ( s + 2 ) & + K ( s + 5 ) \\
s^2 + (K+1)s &+ 5K-2.
\end{align*} $$
با تطبیق معادله مشخصه مطلوب و معادله مشخصه بالا، داریم:
$$ \large \begin {align*}
s ^ 2 + 4 s + 1 3 & = s ^ 2 + ( K + 1 ) s + 5 K - 2 \\
\implies K + 1 & = 4 , 5 K - 2 = 1 3 .
\end {align*} $$
در نهایت $$ K=3 $$ به دست میآید.
با استفاده از معادله (۶)، خطای حالت ماندگار برابر با $$ \left | \dfrac { 1 } { 1- \frac { K z } { p } } \right | = \dfrac { 1 } { 6 . 5 } \approx 1 5 \% $$ است.
به عنوان جمعبندی از آنچه درباره کنترل PD و PI و جبران ساز پیش فاز و پس فاز گفتیم:
- کنترل PD
- پایداری را فراهم میکند و به ما اجازه میدهد مشخصات پاسخ گذرا را شکل دهیم.
- کنترلکننده مشتقی $$ Ks $$ را با یک کنترلکننده علی و پایدار پیش فاز $$ K \dfrac{s+z}{s+p} $$ جایگزین میکند که در آن $$ p > z $$ است.
- یک صفر $$ -z $$ در سمت چپ صفحه مختلط قرار میدهد و در نتیجه، مکان ریشه را به سمت چپ صفحه مختلط انتقال میدهد؛ اما شکل مکان بسته به بزرگی $$ p $$ تفاوت دارد.
- کنترل PI
- پایداری و ردیابی حالت ماندگار را مراجع ثابت به خوبی انجام میدهد.
- کنترلکننده انتگرالی $$ \frac{K}s $$ با یک کنترلکننده پایدار پیش فاز $$ K \dfrac{s+z}{s+p} $$ جایگزین میشود که در آن $$ p < z $$ است و شکل مکان ریشه را در مقایسه با PI تغییر نمیدهد.
بنابراین، با ترکیب کنترل PI و PD یا تقریبهای آنها، یعنی جبران ساز پس فاز و جبران ساز پیش فاز میتوان کنترل PID را به دست آورد که مشخصات هر دو را داشته باشد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی کنترل
- آموزش کنترل مدرن – حل ۱۰۰ مساله
- مجموعه آموزشهای مهندسی برق
- آموزش کنترل مدرن به همراه پیاده سازی در متلب
- سیستم کنترل حلقه باز — به زبان ساده
- تقلب نامه (Cheat Sheet) کنترل خطی
- پاسخ سیستم مرتبه دوم — از صفر تا صد
^^










