الگوریتم های جستجو در هوش مصنوعی – توضیح به زبان ساده

در سالهای اخیر، اهمیت استفاده از الگوریتمهای جستجو در «یادگیری ماشین» (Machine Learning)، «یادگیری عمیق» (Deep Learning) و بهطور کلی «هوش مصنوعی» (Artificial Intelligence | AI) بیش از پیش آشکار شده است. ارائه راهحل برای مسائل مرتبط با هوش مصنوعی را میتوان از جمله دلایل این اهمیت برشمرد. الگوریتم جستجو، روشی پایهای برای پایش و یافتن بهینهترین پاسخ در فضای مسئله است. در این مطلب از مجله فرادرس، ابتدا به توضیح مفهوم الگوریتم های جستجو در هوش مصنوعی میپردازیم و پس از آشنایی با اصطلاحات رایج و همچنین انواع الگوریتمهای جستجو، چند نمونه کاربردی را نیز بررسی میکنیم.
در این مطلب، ابتدا تعریفی از الگوریتمهای جستجو در هوش مصنوعی را بیان میکنیم. در ادامه، اصطلاحات رایج در این موضوع را مرور خواهیم کرد. بعد از بیان شاخصهای ارزیابی عملکرد، انواع الگوریتمهای جستجو در هوش مصنوعی را بیان میکنیم که ازجمله آنها میتوان به جستجوی اول عمق و و اول سطح اشاره کرد. جستحوی هزینه یکنواخت و الگوریتمهای جستجوی آگاهانه، سایر موضوعات این مطلب را پوشش میدهند. در انتهای این مطلب نیز، کاربردهای الگوریتمهای جستجو در هوش مصنوعی را بیان میکنیم.
منظور از الگوریتم های جستجو در هوش مصنوعی چیست؟
الگوریتم های جستجو در هوش مصنوعی، الگوریتمهایی هستند که برای حل مسائل جستجو از آنها استفاده میشود. یک مسئله جستجو از سه بخش کلی تشکیل میشود:
- «فضای جستجو» (Search Space)
- «موقعیت شروع» (Start State)
- «موقعیت هدف» (Goal State)
الگوریتم های جستجو در هوش مصنوعی، با بررسی راهکارهای مختلف، «عامل هوشمند» (Ai Agent) را در مسیر رسیدن به موقعیت هدف راهنمایی میکنند. این دسته از الگوریتمها، با تبدیل موقعیت شروع به موقعیت ایدهآل، راهحلهایی جستجو-محور را پدید میآورند. در نتیجه، اجرای توابع جستجو و کشف راهحالهای قابل اجرا، قدمی لازم و ضروری برای استفاده از الگوریتمهای جستجو است. عامل هوشمند، وظیفه انجام و به سرانجام رساندن کارهایی را که به نتیجه دلخواه منتهی میشوند بر عهده دارد.

اصطلاحات رایج
هر مسئله در حوزه هوش مصنوعی را میتوان از طریق اصطلاحات زیر تعریف کرد:
- «انتقال» (Transition): به عمل جابهجایی میان موقعیتهای مختلف گفته میشود.
- «فضای جستجو» (Search Space): به مجموع تمام موقعیتهای موجود در مسئله گفته میشود.
- «موقعیت شروع» (Start State): موقعیتی که عامل هوشمند، فرایند جستجو را از آنجا شروع میکند.
- «موقعیت میانی» (Intermediate State): موقعیتهایی که در فاصله میان موقعیت شروع و پایان واقع شدهاند و باید پیمایش شوند.
- «موقعیت هدف» (Goal State): موقعیتی که در آن، فرایند جستجو به پایان میرسد.
- «درخت جستجو» (Search Tree): طرحوارهای به شکل درخت برای نمایش مسئله. وضعیت شروع در درخت جستجو، «گره ریشه» (Root Node) یا همان موقعیت شروع نام دارد.
- «عمل» (Action): تمامی انتخابهایی که در دسترس عامل هوشمند است.
شاخص های ارزیابی عملکرد
برای ارزیابی عملکرد هر یک از الگوریتمهای جستجو، از چهار شاخص زیر بهره میبریم:
- «کامل بودن» (Completeness): یک الگوریتم جستجو کامل است؛ اگر در صورت وجود، به ازای هر ورودی تصادفی، راهحلی پیدا کند.
- «بهینگی» (Optimality): راهحل یک الگوریتم، بهینه است؛ اگر بهترین راهحل یعنی کم هزینهترین، در میان تمامی راهحلهای موجود باشد.
- «پیچیدگی زمانی» (Time Complexity): مدت زمانی که طول میکشد تا اجرای یک الگوریتم به پایان برسد.
- «پیچیگی فضایی» (Space Complexity): حداکثر حافظهای که الگوریتم برای اجرا به آن نیاز دارد.
انواع الگوریتم های جستجو در هوش مصنوعی
بهطور کلی، الگوریتمهای جستجو را میتوان به دو گروه «جستجوی ناآگاهانه» (Uninformed Search) و «جستجوی آگاهانه» (Informed Search) دستهبندی کرد.
در این مطلب به توضیح و شرح سه روش از هر گروه و در مجموع شش روش از پرکاربردترین انواع این الگوریتمها در هوش مصنوعی میپردازیم.
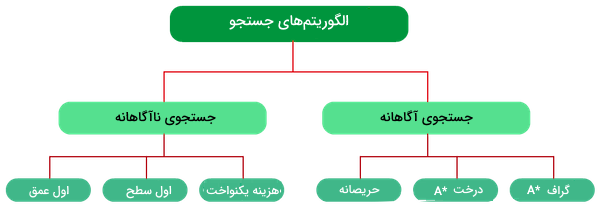
الگوریتم های جستجوی ناآگاهانه
الگوریتمهای جستجوی ناآگاهانه، علاوهبر اطلاعاتی که مسئله در اختیار ما قرار میدهد، اطلاعات اضافه دیگری درباره موقعیت هدف و هزینه انتقال میان موقعیتها به ما ارائه نمیدهند. تفاوت مسیرهای مختلف برای رسیدن به موقعیت هدف از موقعیت شروع، تنها با ترتیب و یا طول هر عمل مشخص میشود. به الگوریتم جستجوی ناآگاهانه، «جستجوی کورکورانه» (Blind Search) نیز گفته میشود. توانایی این الگوریتمها، در ایجاد موقعیتهای جدید و همچنین ایجاد تمایز میان موقعیت هدف و دیگر موقعیتها خلاصه میشود. به عنوان سه نمونه مهم از این الگوریتمها میتوان به موارد زیر اشاره کرد:
- روش «جستجوی اول عمق» (Depth-First Search | DFS)
- روش «جستجوی اول سطح» (Breadth-First Search | BFS)
- روش «جستجوی هزینه یکنواخت» (Uniform Cost Search | UCS)
هر یک از روشهای ذکر شده، شامل اجزای زیر هستند:
- گراف مسئله با دو گره شروع و پایان، که به ترتیب با حروف S و G نشانهگذاری میشوند.
- رویکردی برای حل مسئله؛ شامل روش پیمایش گراف برای رسیدن به گره G.
- لیستی به نام لیست انتقالی، برای ذخیره تمام موقعیتهای ممکنی که میتوان از موقعیت فعلی به آنها منتقل شد.
- طرحواره درختی، که همزمان با حرکت به سمت گره هدف ایجاد میشود.
- ترتیب پیمایش گرهها از گره S به G، که در واقع همان نقشه راه است.
جستجوی اول عمق
جستجوی اول عمق یا الگوریتم DFS، الگوریتمی برای پیمایش درخت یا ساختار داده «گراف» (Graph) است. این الگوریتم کار خود را با انتخاب گرهای به عنوان گره ریشه آغاز کرده و سپس هر شاخه از درخت را پیش از عقبگرد و انتقال به شاخه بعدی، تا انتها پیمایش میکند. از آنجایی که الگوریتم DFS از رویکرد «ورودی-آخر-خروجی-اول» (Last-in-First-out | LIFO) برای پیگیری گرههای ملاقات شده استفاده میکند، پیادهسازی آن با بهرهگیری از ساختمان داده «پشته» (Stack) انجام میشود. در ادامه مثالی از این روش را با هم بررسی میکنیم.
مثال جستجوی اول عمق
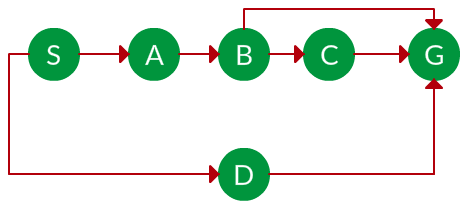
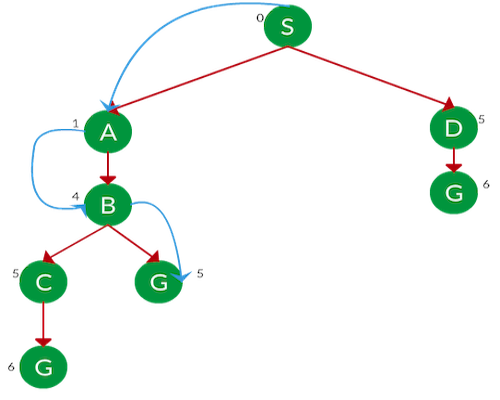
در گراف زیر، الگوریتم DFS چه مسیری را برای انتقال از گره S به گره G پیدا میکند؟
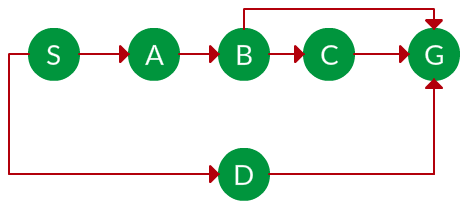
پاسخ: الگوریتم DFS همیشه عمیقترین شاخه را تا زمان رسیدن به گره هدف، یا تمام شدن سایر گرهها انتخاب و پیمایش میکند. همانطور که در تصویر زیر مشاهده میشود:
- ابتدا و در گره S، شاخه عمیقتر یعنی سمت چپ را انتخاب و به گره A منتقل میشود.
- گره A تنها یک یال دارد. در نتیجه به گره B منتقل میشود.
- از آنجا که گره B از دو شاخه تشکیل شده است، شاخه عمیقتر یعنی سمت چپ را انتخاب و به گره C منتقل میشود.
- گره C تنها یک یال دارد. در نتیجه به گره هدف یا همان G ختم میشود.
مسیر حرکت: S → A → B → C → G
ویژگیهای الگوریتم DFS
از جمله ویژگیهای الگوریتم جستجوی اول عمق، میتوان به موارد زیر اشاره کرد:
- نشان : بیانگر عمق یا همان تعداد سطوح درخت جستجو.
- نشان : بیانگر تعداد گرهها در سطح اُم درخت.
- کامل بودن: الگوریتم DFS کامل است، اگر درخت جستجو «متناهی» (Finite) باشد. به این معنی که در صورت وجود راهحل، الگوریتم DFS قادر به پیدا کردن آن باشد.
- بهینگی: در الگوریتم DFS، تعداد مراحل لازم یا هزینه صرف شده برای رسیدن به راهحل زیاد است. در نتیجه الگوریتم بهینهای نیست.
- پیچیدگی زمانی: برابر با تعداد گرههای پیمایش شده.
- پیچیگی فضایی: برابر با حداکثر اندازه لیست انتقالی.
جستجوی اول سطح
جستجوی اول سطح یا الگوریتم BFS نیز الگوریتمی برای پیمایش و جستجو درخت یا گراف است. این الگوریتم، فرایند جستجو را از گره ریشه درخت یا گرهای دلخواه از ساختار داده گراف که با نام «کلید جستجو» (Search Key) شناخته میشود شروع کرده و پس از ملاقات کردن تمامی گرههای یک عمق مشخص، به عمق بعدی میرود.
مثال جستجوی اول سطح
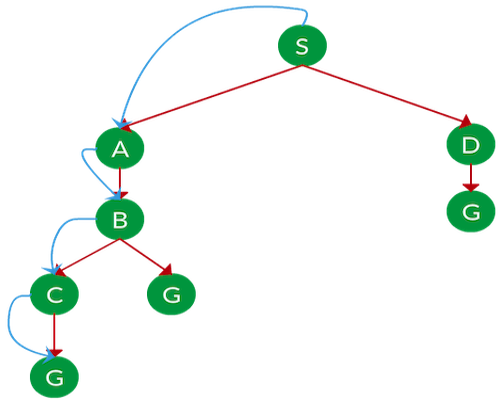
در گراف زیر، الگوریتم BFS چه مسیری را برای انتقال از گره S به گره G پیدا میکند؟
پاسخ: الگوریتم BFS، تا زمان رسیدن به گره هدف یا تمام شدن سایر گرهها و انتقال به شاخه بعدی، کمعمقترین شاخهها را برای پیمایش انتخاب میکند. مانند تصویر زیر:
- ابتدا و در گره شروع یا همان S، شاخه کمعمقتر یعنی شاخه سمت راست را انتخاب و به گره D منتقل میشود.
- گره D تنها یک یال دارد؛ پس همان یال را انتخاب و به گره G ختم میشود.
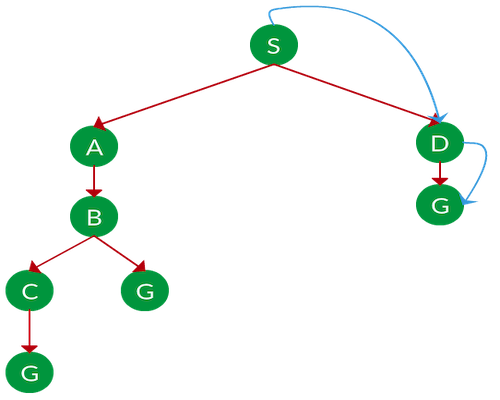
مسیر حرکت: S → D → G
ویژگیهای الگوریتم BFS
برخی از ویژگیهای الگوریتم جستجوی اول سطح به شرح زیر است:
- نشان : بیانگر عمق کوتاهترین مسیر.
- نشان : بیانگر تعداد گرهها در سطح اُم درخت.
- کامل بودن: الگوریتم BFS کامل است؛ به این معنی که در صورت وجود راهحل، الگوریتم BFS آن را پیدا میکند.
- بهینگی: الگوریتم BFS بهینه است؛ تا زمانی که هزینه انتقال از تمامی «یالها» (Edges) برابر باشد.
- پیچیدگی زمانی: برابر با تعداد گرههای پیمایش شده در کوتاهترین مسیر.
- پیچیگی فضایی: برابر با حداکثر اندازه لیست انتقالی.
جستجوی هزینه یکنواخت
نحوه عملکرد جستجوی هزینه یکنواخت یا الگوریتم UCS، با دو روش قبلی متفاوت است؛ در این الگوریتم، دیگر هزینه انتقال و جابهجایی از یالهای مختلف، یکسان نیست. از همین رو، هدف پیدا کردن مسیری با کمترین هزینه انباشته است. منظور از هزینه انباشه برای یک گره خاص، مجموع هزینه تمامی یالها، از گره ریشه تا آن گره است.
هزینه یک گره، مانند زیر تعریف میشود:
cost(node) = هزینه انباشته تمامی گرههای پیمایش شده از گره ریشه
به عنوان مثال، هزینه گره ریشه همیشه برابر با صفر است:
cost(root) = 0
مثال جستجوی هزینه یکنواخت
در گراف زیر، الگوریتم UCS چه مسیری را برای انتقال از گره S به گره G پیدا میکند؟
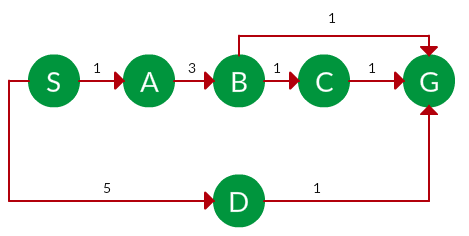
پاسخ: در الگوریتم UCS، هزینه هر گره، برابر است با هزینه انباشته از گره ریشه تا آن گره. در این این الگوریتم، مسیری به عنوان راهحل انتخاب میشود که کمترین هزینه را داشته باشد. توجه داشته باشید که به دلیل وجود انتخابهای زیاد در لیست انتقالی، تا زمانی که هزینه پایین باشد، الگوریتم UCS تمامی مسیرها را پیمایش کرده و پس از پیدا کردن مسیری کمهزینهتر، مسیرهای قبلی را حذف میکند. در تصویر زیر تنها مسیر منتخب ترسیم شده است.
- گره S دو زیر شاخه دارد. هزینه انتقال به شاخه سمت چپ برابر با ۱ و شاخه سمت راست برابر با ۵ است. پس یال کمهزینهتر، یعی سمت چپ را انتخاب و به گره A منتقل میشود.
- گره A تنها یک یال دارد؛ در نتیجه از طریق همان یال و با هزینه ۳، به گره B منتقل میشود.
- گره B شامل دو زیر شاخه است. یال سمت راست با هزینه ۱ به گره G رسیده و یال سمت چپ با هزینه ۱ به گرهای غیر از گره هدف منتهی میشود. در نتیجه یال سمت راست را انتخاب و به گره G ختم میشود.
مسیر حرکت: S → A → B → G
هزینه مسیر: ۵
ویژگیهای الگوریتم UCS
به عنوان ویژگیهای الگوریتم جستجوی هزینه یکنواخت، میتوان به موارد زیر اشاره کرد:
- نشان : هزینه مسیر منتخب.
- نشان : هزینه یال.
- عمق موثر: .
- پیچیدگی زمانی: .
- پیچیگی فضایی: .
مزیتها
برخی از مزیتهای الگوریتم جستجوی هزینه یکنواخت به شرح زیر است:
- الگوریتم UCS در صورتی کامل است که موقعیتها متناهی بوده و حلقهای با وزن صفر نیز وجود نداشته باشد.
- الگوریتم UCS بهینه است؛ اگر هزینه منفی وجود نداشته باشد.
معایب
الگوریتمهای جستجوی هزینه یکنواخت در کنار مزیتها، معایبی نیز دارند، از جمله:
- پیمایش تمامی گرهها در هر جهت ممکن
- نداشتن اطلاعات کافی درباره موقعیت هدف

الگوریتم های جستجوی آگاهانه
الگوریتمهای جستجوی آگاهانه، اطلاعاتی درباره موقعیت هدف در اختیار دارند که به آنها در انجام فرایند جستجویی موثر کمک میکند. به این اطلاعات اضافه «هیوریستیک» (Heuristic) گفته میشود. در این بخش از مطلب مجله فرادرس، به شرح سه مورد از این الگوریتمها میپردازیم:
- روش «جستجوی حریصانه» (Greedy Search)
- روش جستجوی درخت *A
- روش جستجوی گراف *A
در جستجوی آگاهانه، تابع هیوریستیک، نزدیکی فاصله یک موقعیت به موقعیت هدف را تخمین میزند. از جمله توابع هیوریستیک نمونه، میتوان به «فاصله اقلیدسی» (Euclidean Distance) و «فاصله منهتن» (Manhattan Distance) اشاره کرد. در الگوریتمهای جستجوی آگاهانه مختلف، از توابع هیوریستیک متفاوتی استفاده میشود.
جستجوی حریصانه
هدف در روش جستجوی حریصانه، بسط دادن نزدیکترین گره به گره هدف است. تخمین این «نزدیکی» (Closeness)، از طریق تابع هیوریستیک محاسبه میشود. هرقدر خروجی این تابع کوچکتر باشد، یعنی گره مورد نظر به هدف نزدیکتر است. در نتیجه، گرهای بسط داده میشود که به گره هدف نزدیکتر باشد.
جستجوی حریصانه، در بدترین حالت، ممکن است نتیجهای برابر با الگوریتم DFS داشته باشد. اما بهطور معمول، برای مسائلی که تعداد گره کمی دارند، نتیجه خوبی را حاصل میدهد.
مثال جستجوی حریصانه
با استفاده از روش جستجوی حریصانه، مسیر حرکت از گره S به گره G را پیدا کنید. در تصویر زیر، مقدار تابع هیوریستیک در پایین هر گره درج شده است.
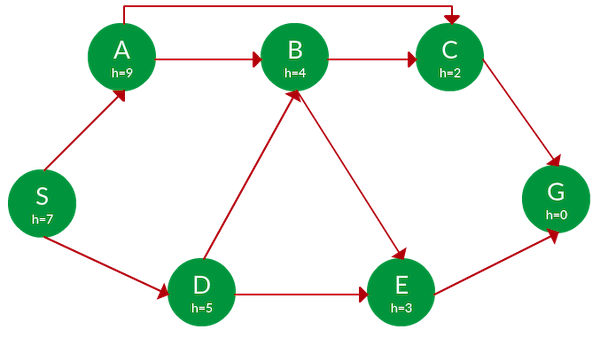
پاسخ: تابع هیوریستیک h(x)، الگوریتم جستجوی حریصانه را قادر میسازد تا در هر مرحله، نزدیکترین گره به گره هدف را پیدا کند.
- با شروع از گره S، میتوان به یکی از دو گره A با مقدار هیوریستیک ۹ یا گره D با هیوریستیک ۵ منتقل شد. از آنجایی که هدف ما انتخاب گرهای با نزدیکترین فاصله به هدف است، گره D را انتخاب میکنیم.
- انتخاب بعدی از گره D، میتواند گره B با هیوریستیک ۴ یا گره E با هیوریستیک ۳ باشد. مجدد گرهای که هزینه کمتری دارد، یعنی E را انتخاب کرده و به آن منتقل میشویم.
- در آخر، از گره E به گره G با هیوریستیک صفر منتقل میشویم.
مسیر پیمایش، با رنگ آبی در تصویر زیر مشخص شده است:
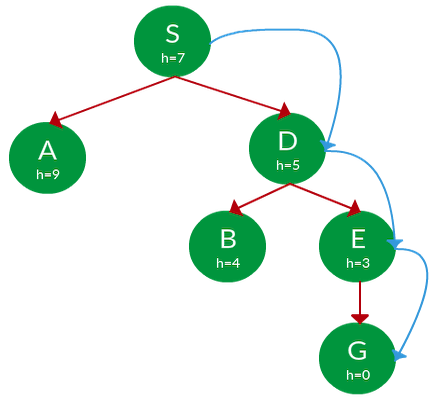
مسیر حرکت: S → D → E → G
جستجوی درخت *A
روش جستجوی درخت *A، در واقع ترکیبی است از نقاط قوت دو روش جستجوی هزینه یکنواخت و جستجوی حریصانه. در این روش، جمع تابع هزینه الگوریتم UCS با نماد g(x) و تابع هزینه جستجوی حریصانه با نماد h(x)، تابع هیوریستیک را تشکیل میدهند. تعریف تابع هیوریستیک در روش جستجوی درخت *A مانند زیر است:
- در این تعریف، h(x) که به آن «هزینه رو به جلو» (Forward Cost) نیز گفته میشود، تخمینی از فاصله گره فعلی تا گره هدف است.
- تابع g(x) یا «هزینه رو به عقب» (Backward Cost)، هزینه انباشته از گره ریشه تا گره فعلی است.
- روش *A، زمانی بهینه است که تخمین تابع h(x) از هزینه حقیقی فاصله تا گره هدف، یعنی h*(x) کمتر باشد. به این ویژگی از تابع هیوریستیک الگوریتم *A، «پذیرفتگی» (Admissibility) میگویند.
- در این روش، هدف انتخاب گرهای با کمترین مقدار f(x) است.
معیار پذیرفتگی مانند زیر تعریف میشود:
مثال جستجوی درخت *A
با استفاده از روش جستجوی درخت *A، مسیر حرکت از گره S به G را پیدا کنید.
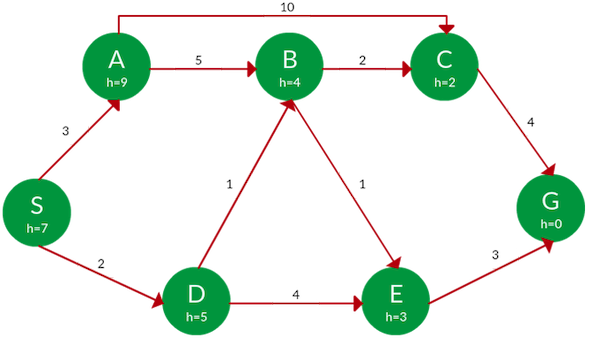
پاسخ: الگوریتم با شروع از گره S، تابع هیوریستیک که مجموع دو تابع g(x) و h(x) بود را برای تمامی گرههای موجود در لیست انتقالی حساب میکند. سپس گرهای که کمترین مجموع را داشته باشد برای قدم بعدی انتخاب میشود. توجه داشته باشید که اگر در یک مرحله از الگوریتم، دو گره هزینه یکسانی داشتند، ابتدا هر دو آنها را بسط داده، و در مرحله بعدی، گرهای که جمع هزینه کمتری داشته باشد را انتخاب میکنیم (مانند ردیف ششم و هفتم در جدول). مراحل کامل انتخاب مسیر با استفاده از روش *A در جدول زیر آمده است:
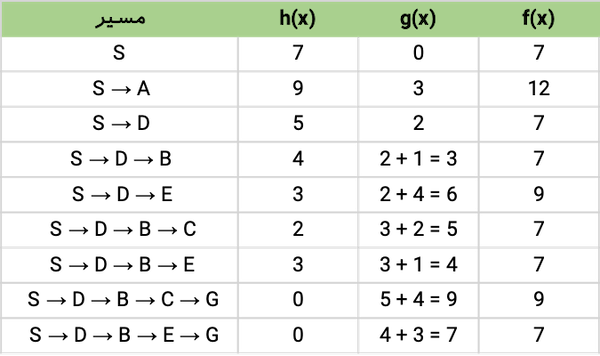
مسیر حرکت: S → D → B → E → G
هزینه مسیر: ۷
جستجوی گراف *A
روش جستوی درخت *A، نتایج خوبی را ارائه میدهد؛ اما از آنجایی که چندین مرتبه هر شاخه را پیمایش میکند، کمی زمانبر است. در واقع اگر گره یکسانی، دو مرتبه در شاخههای متفاوت یک درخت بسط داده شده باشد، این احتمال وجود دارد که روش جستجوی درخت *A، هر دو شاخه را پیمایش و در نتیجه باعث اتلاف زمان شود. اما در روش جستجوی گراف *A، این قانون وجود دارد که هر گره باید فقط و فقط یک مرتبه بسط داده شود. جستجوی گراف بهینه است اگر تفاضل هزینه رو به جلو دو گره متوالی، کمتر یا برابر با هزینه رو به عقب میان همان دو گره باشد. به این ویژگی تابع هیوریستیک جستجوی گراف، «ثبات» (Consistency) گفته میشود.
تعریف معیار ثبات در جستجوی گراف به صورت زیر است:
مثال جستجوی گراف *A
با استفاده از روش جستجوی گراف *A، مسیر حرکت از گره S به G را پیدا کنید.

پاسخ: روش حل و پیدا کردن مسیر بهینه مانند جستجوی *A است؛ با این تفاوت که، گرههای بسط داده شده ثبت میشوند، تا مجدد توسط الگوریتم پیمایش نشوند.
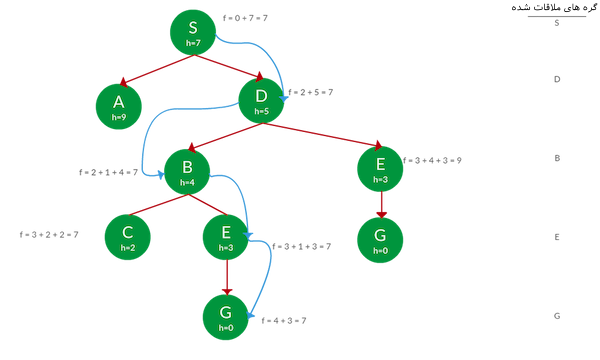
مسیر حرکت: S → D → B → E → G
هزینه مسیر: ۷
کاربردهای الگوریتم های جستجو در هوش مصنوعی چیست؟
از آنجا که با استفاده از الگوریتمهای جستجو میتوان بهینهترین راهحلها را در یک مسئله پیدا کرد، کاربرد این الگوریتمها در حوزه هوش مصنوعی نیز بسیار است. در ادامه این مطلب، به چند نمونه از این کاربردها اشاره میکنیم.
حل مسئله
بهرهمندی الگوریتمهای جستجو از ساز و کارهایی همچون شرح مسئله و فضای جستجو، موجب شده است تا استفاده از آنها در هوش مصنوعی روز به روز بیشتر شود. به عنوان نمونه، میتوان کاربردهایی چون مسیریابی، در ابزارهایی مانند «نقشه گوگل» (Google Maps) را مثال زد که در آن با استفاده از الگوریتمهای جستجو، راهحلی کاربردی برای مسئلهای مهم در جهان حقیقی ایجاد شده است. در این نرمافزارها، از روشهای جستجو برای پیدا کردن کوتاهترین و سریعترین مسیر، میان دو موقعیت مکانی استفاده میشود.
پیاده سازی
بسیاری از فعالیتهای مرتبط با حوزه هوش مصنوعی را میتوان در غالب الگوریتمهای جستجو بازتعریف کرد. راهکاری که موجب بهبود فرمولبندی راهحل یک مسئله میشود. مهندسین نرمافزار میتوانند با بهرهگیری از انواع مختلف الگوریتمهای جستجو که در این مطلب از مجله فرادرس نیز به چند نمونه مهم آن اشاره شد و همچنین با طراحی الگوریتمهایی هدفمند در فضای جستجویی از پیش تعریف شده، مسائل مختلف را به نوعی مدل محاسباتی تبدیل کنند.
عامل های مبتنی بر هدف
یکی دیگر از کاربردهای الگوریتم های جستجو در هوش مصنوعی، افزایش بهرهوری «عاملهای مبتنی بر هدف» (Goal-Based Agents) است. الگوریتمهای جستجو به عاملهای مبتنی بر هدف این امکان را میدهند تا با جابهجایی در فضای مسئله و بهمنظور رسیدن به هدفی مشخص، در محیطی آزمایشی شروع به فعالیت کرده و بهینهترین مجموعه عملها را پیدا کنند. از دیگر کاربردهای الگوریتمهای جستجو، حدف مسیرهای جستجوی غیرضروری و در نتیجه افزایش سرعت نتیجهگیری برای عاملهای هوشمند است.
پشتیبانی سیستم های تولید
الگوریتم های جستجو در هوش مصنوعی را میتوان به عنوان یکی از عوامل اجرایی مهم در «سیستمهای تولید» (Production Systems) در نظر گرفت. با بهرهگیری از قوانین و روشهای موجود در این سیستمها، میتوان کاربردهای هوش مصنوعی را در عمل به اجرا گذاشت. سیستمهای تولید، برای پیدا کردن قواعدی که منجر به مجموعه اقدامات ضروری میشوند، از الگوریتم های جستجو در هوش مصنوعی استفاده میکنند.
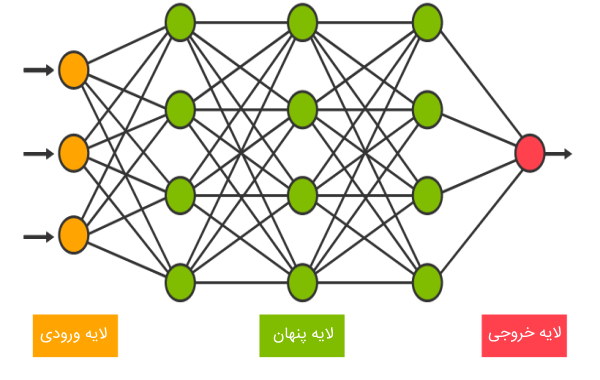
شبکه های عصبی
«شبکههای عصبی» (Neural Networks)، سیستمهای محاسباتی هستند مشکل از یک یا چند «لایه پنهان» (Hidden Layer)، یک «لایه ورودی» (Input Layer) و یک «لایه خروجی» (Output Layer)، که هر لایه نیز، از تعدادی گره یا «نود» (Node) تشکیل شده است. از شبکههای عصبی برای اجرای فرایندهای بسیاری در هوش مصنوعی استفاده میشود. به عنوان مثال، جستجو برای پیدا کردن «پارامترهای وزنی» (Weight Parameters)، یکی از کاربردهای الگوریتمهای جستجو در شبکههای عصبی است.
جمعبندی
الگوریتمهای جستجو نقش بسیار مهمی را به عنوان ابزاری برای حل مسئله و تصمیمگیری در حوزه هوش مصنوعی بر عهده دارند. دو روش جستجوی ناآگاهانه و آگاهانه، به سیستمهای هوشمند این امکان را میدهند، تا راهحلی برای مسائل پیچیده مرتبط با هوش مصنوعی پیدا کنند. در این مطلب از مجله فرادرس، ابتدا با مفهوم الگوریتمهای جستجو و چند روش پرکاربرد آن در هوش مصنوعی آشنا شدیم و سپس برای درک بهتر، چند کاربرد مهم آن در زمینههای مختلف را نیز بررسی کردیم.













