کار چیست؟ – فیزیک به زبان ساده

هنگامی که نیرویی بر جسمی وارد شود و آن را از مکانی به مکان دیگر جابجا کند، کار فیزیکی انجام شده است. برای آن‌که مقدار کار را به‌دست آوریم، به دانستن سه کمیت نیرو، مقدار جابجایی و زاویه بین نیرو و جابجایی، نیاز داریم. به بیان دیگر، کار برابر حاصل‌ضرب نیرو در جابجایی است. در این مطلب، در ابتدا به پرسش کار چیست پاسخ می‌دهیم و در ادامه در مورد فرمول کار، قضیه کار و انرژی، کار نیروهای پایستار و ناپایستار، کار فنر و کار نیروی جاذبه صحبت خواهیم کرد.

کار چیست ؟

تعریف کار در فیزیک، رابطه آن را با انرژی مشخص می‌کند. هر زمان که کار انجام شود، انرژی منتقل شده است. برای آن‌که کار انجام شود، نیروی خارجی باید بر جسمی وارد شود و آن را در راستای نیروی وارد شده جابجا کند.

مثال‌های زیادی از کار در زندگی روزمره وجود دارند. هنگامی که می‌خواهید به مسافرت بروید، چمدان سنگین را بلند می‌کنید و در ماشین قرار می‌دهید. با بلند کردن و جابجا کردن چمدان، کار فیزیکی انجام داده‌اید. نکته مهم در این مثال، جابجایی جسم پس از اعمال نیرو است. اما باید به این نکته توجه داشته باشیم که جابجایی باید در راستای نیروی وارد شده، صورت بگیرد. اگر تمام نیروی خود را به سنگ بزرگی وارد کنید تا آن‌ را جابجا کنید، آیا کاری انجام داده‌اید؟ اگر سنگ جابجا شود، کار انجام شده است، اما اگر نتوانید سنگ را تکان دهید، علی‌رغم خستگی بسیار، کاری انجام نداده‌اید.

گفتیم اگر جابجایی صفر باشد، کاری انجام نشده است. اکنون حالت دومی را در نظر بگیرید. سینی غذا را با یک‌ دست بلند می‌کنید و آن را بالای سر خود نگه می‌دارید. سپس، با سرعت ثابتی شروع به حرکت می‌کنید. آیا کار انجام می‌دهید؟ به طور حتم پاسخ شما به این پرسش آری است. اما از دیدگاه فیزیکی کاری انجام نشده است. چرا؟

برای نگه داشتن سینی بالای سر، نیرویی بر آن وارد کرده‌اید. جهت نیروی وارد شده به سمت بالا است. همچنین، سینی در راستای افقی جابجا می‌شود. در اینجا، نیرو وارد شده و سینی جابجا شده است، اما آیا جابجایی و نیرو در یک راستا هستند؟ خیر. نیرویی که وارد می‌کنید سبب جابجایی سینی در راستای عمودی نشده است. بار دیگر به این عبارت مهم توجه کنید:

برای آن‌که جابجایی انجام شود، نیرو باید مولفه‌ای در راستای جابجایی داشته باشد. 

برای درک بهتر این عبارت، به مثال دیگری توجه کنید. صبح پس از آماده شدن، کو‌له‌پشتی سنگین خود را برمی‌دارید و مسافت طولانی را پیاده راه می‌روید. احساس خستگی بسیار می‌کنید و با خود فکر می‌کنید «من امروز چقدر کار انجام دادم». از دیدگاه فیزیک، شما کاری انجام نداده‌اید. چرا؟ به کوله‌پشتی نیرو وارد و آن را جابجا کرده‌اید. آیا نیروی وارد شده و جابجایی در یک راستا هستند؟ خیر. نیرو بر جابجایی عمود است، بنابراین مقدار کار انجام شده برابر صفر خواهد بود.

پس از آشنایی با مفهوم کار چیست، در مورد فرمول کار و نحوه محاسبه آن صحبت می‌کنیم.

فرمول کار چیست ؟

گفتیم برای آن‌که کاری انجام شود، نیروی خارجی باید بر جسم وارد شود و جسم باید در راستای نیروی وارد شده جابجا شود. در نتیجه، برای به‌دست آوردن کار نیاز به مولفه نیرو در راستای جابجایی داریم. تعریف کار به زبان ریاضی به صورت ضرب داخلی نیرو در جابجایی و به صورت زیر نوشته می‌شود:

$$W = (F\ cos\theta) \ d = \overrightarrow{F}.\overrightarrow{d}$$

برای رابطه فوق داریم:

• W برابر کار انجام شده توسط نیروی وارد شده است.
• F نیرویی است که بر جسم وارد می‌شود و آن را به اندازه مشخصی جابجا می‌کند.
• $$\theta$$ زاویه بین بردارهای نیرو و جابجایی است.

دیمانسیون کار و انرژی یکسان و برابر $$[ML^2T^{-2}]$$ است.

تا اینجا آموختیم که کار چیست و در مورد فرمول کار صحبت کردیم. در ادامه، در مورد و واحد کار و روش محاسبه کار در فیزیک صحبت خواهیم کرد.

واحد کار چیست ؟

واحد SI کار، ژول است. یک ژول به صورت کار انجام شده توسط نیرویی برابر یک نیوتن برای جابجایی جسم به اندازه یک متر در راستای نیرو، تعریف می‌‌شود.

تاکنون به پرسش کار چیست به زبان ساده پاسخ دادیم. در ادامه، در مورد نحوه محاسبه کار در فیزیک صحبت خواهیم کرد.

روش محاسبه کار چیست ؟

با فرمول کار و پرسش کار چیست آشنا شدیم. برای محاسبه کار نیاز به دانستن مقدار نیرو و جابجایی انجام شده در راستای نیرو، داریم. برای محاسبه کار، دو حالت را در نظر می‌گیریم. در حالت نخست، فرض می‌کنیم که تنها یک نیرو بر جسم وارد می‌شود. به مثال‌های زیر توجه کنید.

تاکنون با فرمول کار و وابستگی آن به نیرو و جابجایی آشنا شدیم. آیا می‌دانید نقش نیرو و جابجایی و زاویه بین آن ها در محاسبه کار چیست؟ مثال زیر به شما در پاسخ به این پرسش کمک خواهد کرد.

مثال اول روش محاسبه کار

نیرویی برابر ۱۰۰ نیوتن در راستای افقی بر جسمی به جرم ۱۵ کیلوگرم وارد می‌شود و آن را به اندازه ۵ متر در راستای افقی جابجا می‌کند. مقدار کار انجام شده را به‌دست آورید.

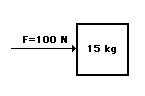
پاسخ: رابطه ریاضی کار عبارت است از:

$$W=Fd\ cos\theta$$

مقدار نیرو برابر ۱۰۰ نیوتن و جسم به اندازه ۵ متر جابجا شده است. همچنین، زاویه بین نیرو و جابجایی برابر صفر است. در نتیجه، داریم:

$$W = (100 \ N)\times(5 \ m)\times cos (0^o) = 500 \ J$$

آیا می دانید نقش نقش نیرو در محاسبه کار چیست؟ در ادامه، مثالی در این رابطه حل می‌شود.

مثال دوم روش محاسبه کار

نیرویی برابر ۱۰۰ نیوتن با زاویه‌ای برابر ۳۰ درجه نسبت به افق به جسمی به جرم ۱۵ کیلوگرم وارد می‌شود. اگر جسم به اندازه ۵ متر در راستای افقی جابجا شود، مقدار کار انجام شده را به‌دست آورید.

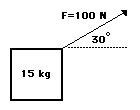
پاسخ: مقدار کار و جابجایی، داده شده است. در مثال ۱، نیرو و جابجایی در یک راستا قرار داشتند. بنابراین، زاویه بین آن‌ها برابر صفر درجه بود. در این مثال، نیروی وارد شده با افق و در نتیجه با بردار جابجایی زاویه ۳۰ درجه ساخته است. مقدار کار انجام شده به صورت زیر به‌دست می‌آید:

$$W = (100 \ N)\times(5 \ m)\times cos (30^o) = 433 \ J$$

در دو مثال بالا در مورد زاویه‌های کمتر از ۹۰ درجه بین نیرو و جابجایی صحبت کردیم. آیا می دانید نقش زاویه‌های ۹۰ درجه و بیشتر در محاسبه کار چیست؟

مثال سوم روش محاسبه کار

نیرویی عمودی بر جسمی به جرم ۱۵ کیلوگرم وارد می‌شود و آن‌ را از سطح زمین به اندازه ۵ متر، بالا می‌برد. اگر جسم با سرعت ثابت حرکت کند، مقدار کار انجام شده را محاسبه کنید.

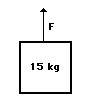
پاسخ: مانند مثال ۱، نیرو و جابجایی در یک راستا قرار گرفته‌اند و زاویه بین آن‌ها برابر صفر درجه است. در نتیجه، داریم:

$$W = (147 \ N)\times(5 \ m)\times cos (0^o) = 735 \ J$$

چرا مقدار نیروی وارد شده برابر ۱۴۷ نیوتن است؟ دو نیرو بر جسم وارد می‌شوند، نیروی وزن و نیروی ‌F به سمت بالا. از آنجایی که جسم با سرعت ثابت حرکت می‌کند، برآیند نیروهای وارد بر آن در راستای افقی و عمودی برابر صفر است. در نتیجه، نیروی F برابر نیروی وزن خواهد بود.

$$F = W = mg = (15 \ kg) \times (9.8 \ \frac{m}{s^2}) = 147 \ N$$

در بیشتر موارد، بیشتر از یک نیرو بر جسم وارد می‌شوند. در این حالت برای محاسبه کار، گام‌های زیر را به ترتیب طی می‌کنیم:

• در ابتدا، تمام نیروهای وارد شده بر جسم را رسم می‌کنیم.
• نمودار جسم آزاد را رسم می‌کنیم.
• نیروهای وارد شده بر جسم را در راستای عمودی و افقی تجزیه می‌کنیم.
• زاویه بین نیروی برآیند را با جابجایی به‌دست می‌آوریم.
• کار را محاسبه می‌کنیم.

برای درک بهتر این مطلب، به مثال‌های زیر توجه کنید:

مثال چهارم روش محاسبه کار

جسمی بر روی سطح افقی بدون اصطکاکی، توسط نیرویی برابر ۱۰ نیوتن کشیده می‌شود. اگر جابجایی آن برابر ۵ متر و به سمت راست باشد، مقدار کار انجام شده را به‌دست آورید.

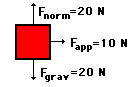
پاسخ: همان‌ گونه که در تصویر مشخص است، سه نیرو بر جسم وارد می‌شوند:

• نیروی وارد شده در راستای افقی.
• نیروی وزن.
• نیروی عمودی سطح.

دو نیروی وزن و نیروی عمودی سطح بر مسیر حرکت جسم عمود هستند، بنابراین کار انجام شده توسط این دو نیرو برابر صفر است. تنها نیروی خارجی وارد شده بر جسم، بر روی آن کار انجام می‌دهد. مقدار کار انجام شده برابر است با:

$$W _ {app} = (10 \ N)\times(5 \ m)\times cos (0^o) = +\ 50 \ J$$

مثال پنجم روش محاسبه کار

نیرویی برابر ۱۰ نیوتن بر جسمی وارد و منجر به کم شدن سرعت حرکت آن می‌شود. اگر جسم پس از طی مسافتی برابر ۵ متر از حرکت بایستد، مقدار کار انجام شده را به‌دست آورید.

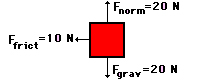
پاسخ: سه نیرو بر جسم وارد می‌شوند: نیروی وزن، نیروی عمودی سطح و نیروی اصطکاک. دو نیروی وزن و عمودی سطح بر جابجایی جسم عمود هستند. بنابراین، مقدار کار انجام شده توسط آن‌ها برابر صفر خواهد بود. نیروی ۱۰ نیوتنی که در خلاف جهت حرکت جسم بر آن وارد می‌شود، همان نیروی اصطکاک است. کار انجام شده توسط این نیرو برابر است با:

$$W _ {fric} = (10 \ N)\times(5 \ m)\times cos (180^o) = -\ 50 \ J$$

نکته: مقدار کار انجام شده منفی است. بنابراین، هنگامی‌که نیروی وارد شده در خلاف جهت جابجایی باشد، مقدار کار منفی به‌دست خواهد آمد.

مثال ششم روش محاسبه کار

جسمی بر روی سطح دارای اصطکاکی قرار گرفته است. نیرویی برابر ۱۰ نیوتن جسم را بر روی سطح می‌کشاند. اگر جسم مسافتی برابر ۵ متر را با سرعت ثابت طی کند، مقدار کار انجام شده را به‌دست آورید.

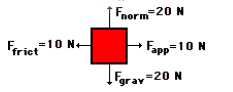
پاسخ: نیروهای وارد شده بر جسم عبارت هستند از:

1. نیروی وزن.
2. نیروی عمودی سطح.
3. نیروی اصطکاک.
4. نیروی وارد شده بر جسم.

دو نیروی وزن و عمودی سطح بر مسیر حرکت جسم عمود هستند، بنابراین کار انجام شده توسط این در نیرو برابر صفر خواهد بود. نیروهای افقی وارد شده بر جسم، نیروی اصطکاک و نیروی وارد شده بر آن هستند. کار انجام شده توسط این دو نیرو برابر است با:

$$W _ {app} = (10 \ N)\times(5 \ m)\times cos (0^o) = +\ 50 \ J$$

$$W _ {fric} = (10 \ N)\times(5 \ m)\times cos (180^o) = -\ 50 \ J$$

مثال هفتم روش محاسبه کار

جسمی به جرم ۲ کیلوگرم بر روی سطح بدون اصطکاکی با سرعت ثابت حرکت می‌کند. مقدار کار انجام شده پس از طی مسافت ۵ متر چه مقدار است؟

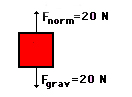
پاسخ: تنها دو نیروی وزن و نیروی عمودی سطح بر جسم وارد می‌شوند. این دو نیرو بر مسیر حرکت جسم عمود هستند، در نتیجه کار انجام شده توسط آن‌ها برابر صفر است.

مثال هشتم روش محاسبه کار

جسمی به جرم ۲ کیلوگرم با نیرویی برابر ۲۰ نیوتن و با سرعت ثابت به سمت بالا کشیده می‌شود. اگر جسم تا ارتفاع ۵ متری از سطح زمین بالا برده شود، مقدار کار انجام شده توسط نیروی وزن و نیروی کشش طناب را به‌دست آورید.

پاسخ: فرض می‌کنیم جسم توسط طنابی به سمت بالا کشیده می‌شود. در نتیجه، نیروهای وارد شده بر جسم، نیروهای وزن و نیروی کشش طناب هستند. هر دو نیرو کار انجام می‌دهند، زیرا در راستای جابجایی قرار دارند. زاویه بین نیروی وزن و بردار جابجایی برابر ۱۸۰ درجه است، بنابراین کار انجام شده توسط این نیرو برابر است با:

$$W _ {mg} = (20 \ N) \times(5 \ m) \times cos (0^o) = -+\ 100 \ J$$

همچنین، زاویه بین نیروی کشش و جابجایی برابر صفر درجه است، بنابراین کار انجام شده توسط این نیرو مثبت و برابر است است با:

$$W _ {T} = (20 \ N) \times(5 \ m) \times cos (180^o) = -\ 100 \ J$$

تاکنون مثال‌هایی در رابطه با حرکت جسم بر روی سطح افقی حل کردیم، آیا می‌دانید نقش سطح شیبدار و زاویه آن در محاسبه کار چیست؟ آیا زاویه سطح شیبدار بر روی کار انجام شده تاثیر می‌گذارد؟

مثال نهم روش محاسبه کار

اتومبیلی به جرم ۲۰۰۰ کیلوگرم پایین سطح شیبداری با شیب متغیر قرار گرفته است. ارتفاع سطح شیبدار را ۶۰ متر در نظر بگیرید. با توجه به جدول زیر، به این پرسش پاسخ دهید:

در کدام زاویه سطح شیبدار، کار بیشتری انجام خواهد شد؟ نیروی وارد شده بر اتومبیل، موازی سطح شیبدار است.

پاسخ: به این موضوع توجه داشته باشید که زاویه‌های داده شده، زاویه سطح شیبدار هستند نه زاویه بین نیرو و جابجایی. در رابطه کار، زاویه خواسته شده، زاویه بین نیرو و جابجایی است.

اگر نیروی وارد شده موازی سطح شیبدار باشد، زاویه $$\theta$$ در رابطه کار برابر صفر خواهد بود. در نتیجه، برای هر یک از حالت‌های داده شده در جدول، مقدار کار انجام شده به طور تقریب برابر است با:

$$W _ {T} = 1.18 \times 10^6\ J$$

بنابراین، زاویه سطح شیبدار بر مقدار کار انجام شده بر روی اتومبیل، تاثیری نخواهد داشت.

حرکت جسم در تمام مثال‌های فوق به یک مرحله تقسیم می‌شد. در مورد حرکت‌های چند مرحله‌ای جه می‌توان گفت؟ آیا می دانید نقش حرکت‌های چند مرحله‌ای در محاسبه کار چیست؟

مثال دهم روش محاسبه کار

چمدانی به وزن ۲۰۰ نیوتن را از سه طبقه به زحمت بالا می‌برید (ارتفاعی برابر ۱۰ متر) و سپس آن را با نیروی افقی برابر ۵۰/۰ نیوتن با سرعت ثابتی برابر ۰/۵ متر بر ثانیه به اندازه ۳۵/۰ متر جابجا می‌کنید. مقدار کار انجام شده در کل مسیر را به‌دست آورید.

پاسخ: مسیر کل حرکت از دو بخش تشکیل شده است:

1. بالا بردن چمدان از پله‌ها (زاویه صفر).
2. جابجایی افقی چمدان (زاویه صفر).

برای حالت یک داریم:

$$W = (200 \ N) \times(10 \ m) \times cos (0^o) = 2000 \ J$$

$$W _ {T} = (50 \ N) \times(35 \ m) \times cos (0^o) = 1750 \ J$$

مقدار کار کل انجام شده برابر جمع جبری این دو کار و برابر ۳۷۵۰ ژول است.

مثال یازدهم روش محاسبه کار

نیرویی برابر ۵۰ نیوتن بر جسمی وارد می‌شود. زاویه این نیرو با افق برابر ۳۰ درجه است. اگر جسم در راستای افقی به اندازه ۳/۰ متر جابجا شود، مقدار کار انجام شده توسط نیروی وارد شده بر آن را به‌دست آورید.

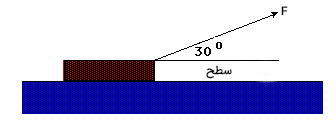
پاسخ: زاویه بین نیرو و جابجایی برابر ۳۰ درجه است، بنابراین مقدار کار انجام شده توسط این نیرو برابر است با:

$$W = (50 \ N) \times(3 \ m) \times cos (30^o) = 129.9 \ J$$

اکنون می‌دانیم کار چیست و با فرمول آن با حل مثال‌های مختلف آشنا شدیم. در ادامه، در مورد رابطه بین کار و انرژی صحبت خواهیم کرد.

رابطه بین کار و انرژی چیست ؟

برای به حرکت درآوردن جسم، باید به آن انرژی منتقل کنیم. انتقال انرژی می‌تواند به شکل اعمال نیرو بر جسم باشد. به مقدار انرژی که توسط نیرو به جسم منتقل می‌شود تا آن را به حرکت درآورد، کار یا کار انجام شده می‌گوییم. بنابراین، رابطه بین کار و انرژی مستقیم است. در واقع، تفاوت بین انرژی جنبشی جسم برابر کار انجام شده توسط آن است. بنابراین، رابطه دیگری برای کار انجام شده توسط جسم به‌دست خواهد آمد:

$$W = \frac{1}{2}m v_f^2 - \frac{1}{2}m v_i^2$$

در رابطه فوق:

• W برابر کار انجام شده توسط جسم و بر حسب ژول است.
• m برابر جرم جسم و بر حسب کیلوگرم است.
• $$v_i$$ برابر سرعت اولیه جسم و بر حسب متر بر ثانیه اندازه گرفته می‌شود.
• $$v_f$$ برابر سرعت نهایی جسم و بر حسب متر بر ثانیه اندازه گرفته می‌شود.

در نتیجه، قضیه کار و انرژی بیان می‌کند:

مقدار کار کل انجام شده توسط نیرو بر روی جسم برابر با تغییرات انرژی جنبشی آن است. 

برای پاسخ به پرسش کار چیست، نمونه سوالات مفهومی در مورد قضیه کار و انرژی در ادامه حل می‌شوند.

نمونه سوالات مفهومی قضیه کار و انرژی

برای درک بهتر پرسش کار چیست و قضیه کار و انرژی، به مثال‌های زیر توجه کنید.

مثال اول قضیه کار و انرژی

انتقال انرژی می‌تواند به چه شکلی باشد؟

1. حرکت
2. انرژی
3. نیرو
4. هیچ‌کدام

پاسخ: پاسخ صحیح گزینه ۳، یعنی نیرو است.

مثال دوم قضیه کار و انرژی

در قضیه کار و انرژی، جرم بر حسب چه واحدی اندازه گرفته می‌شود؟

1. گرم
2. کیلوگرم
3. متر
4. کلوین

پاسخ: پاسخ صحیح گزینه ۲، یعنی کیلوگرم است.

مثال سوم قضیه کار و انرژی

مقدار کار کل انجام شده بر روی جسم برابر با تغییرات:

1. انرژی پتانسیل
2. انرژی جنبشی
3. انرژی شیمیایی
4. انرژی درونی

پاسخ: پاسخ صحیح گزینه ۲، یعنی انرژی جنبشی است.

آیا می‌دانید اثبات قضیه کار و انرژی چگونه است؟ برای اثبات این قضیه، از معادلات حرکت با شتاب ثابت استفاده می‌کنیم.

اثبات قضیه کار و انرژی

برای اثبات این قضیه فرض می‌کنیم که جهت و اندازه نیروهای وارد شده بر جسم و در نتیجه نیروی برآیند ثابت هستند. همچنین، نیرو را موازی جهت سرعت حرکت جسم در نظر می‌گیریم. جسم با شتاب ثابتی برابر a بر روی خط راستی حرکت می‌کند. رابطه بین برآیند نیروی کل و شتاب برابر F=ma است (قانون دوم نیوتن). جابجایی جسم، d، با استفاده از معادله زیر به‌دست می‌آید:

$$v_f^2 = v_i^2 + 2ad \\ d= \frac{v_f^2 - v_i^2}{2a}$$

گفتیم کار برابر با حاصل‌ضرب نیروی وارد شده بر جسم در مقدار جابجایی آن جسم است. با جایگذاری رابطه به‌دست آمده برای جابجایی در معادله کار داریم:

$$W = Fd = m\times a \times \frac{v_f^2 - v_i^2}{2a} = \frac{1}{2} m v_f^2 - \frac{1}{2} mv_i^2 = KE_f - KE_i = \triangle KE$$

حل مسئله‌ های قضیه کار و انرژی

اکنون می‌دانیم کار چیست و با قضیه کار و انرژی و اثبات آن آشنا شدیم. برای درک بهتر این قضیه، مثال‌های مختلفی در ادامه حل شده‌اند.

مثال ۱

برای نگه داشتن اتومبیلی به جرم ۱۲۰۰ کیلوگرم که با سرعت ۹۹ کیلومتر بر ساعت بر خط مستقیمی در حال حرکت است، چه مقدار کار باید انجام شود؟

پاسخ: بر طبق قضیه کار و انرژی، مقدار کار کل انجام شده جسم برابر تغییرات انرژی آن است:

$$W_{net} = K_2 - K_1$$

برای این مثال، مقدار سرعت‌های اولیه و نهایی اتومبیل به ترتیب برابر ۹۹ و صفر کیلومتر بر ساعت هستند. با استفاده از قضیه کار و انرژی داریم:

$$W_{net} = \frac{1}{2}m (v_f^2 - v_i^2) \\ = \frac{1}{2} (1200 \ kg) (0 - (27.5 \ \frac{m}{s})^2)\\ = 453750 \ J$$

برای حل این مثال، کیلومتر بر ساعت را به متر بر ثانیه تبدیل کرده‌ایم:

$$1 \ \frac{km}{h} = \frac{1000}{3600} \ \frac{m}{s}$$

مثال ۲

جسمی به جرم ۶ کیلوگرم در نقطه A با سرعت ۲ متر بر ثانیه و در نقطه B با سرعت ۴ متر بر ثانیه حرکت می‌‌کند. مقدار کار کل انجام شده بر روی جسم وقتی از A به B حرکت می‌کند، چه مقدار است؟

پاسخ: جرم جسم و سرعت‌های آن در دو نقطه مختلف داده شده‌اند. بهترین راه برای حل این مثال، استفاده از قضیه کار و انرژی است.

$$W_{net} = \triangle K \\= \frac{1}{2}m (v_B^2 - v_A^2) \\ = \frac{1}{2} (6 \ kg) ((4 \ \frac{m}{s})^2 - (2 \ \frac{m}{s})^2)\\ = 36 \ J$$

برای داشتن درک بهتری از پرسش کار چیست مثالی در مورد ترمز کردن اتومبیل و مقدار کار انجام شدن در هنگام ترمز حل می‌کنیم.

مثال ۳

اتومبیلی به جرم ۱۶۵۰ کیلوگرم در مدت زمان ۲/۷ ثانیه، سرعت خود را از صفر به ۲۷ متر بر ثانیه می‌رساند. مطلوب است:

1. مقدار شتاب اتومبیل.
2. مقدار جابجایی اتومبیل.
3. مقدار کار انجام شده بر روی اتومبیل.
4. مقدار نیروی متوسط وارد شده بر اتومبیل در این فاصله زمانی.

پاسخ: در ابتدا، قسمت یک را حل می‌کنیم.

قسمت ۱: سرعت اولیه برابر صفر و سرعت نهایی برابر ۲۷ متر بر ثانیه است. تغییرات سرعت در فاصله زمانی ۲/۷ ثانیه رخ داده است. با استفاده از فرمول شتاب ثابت در حرکت بر روی خط راست، داریم:

$$a= \frac{v_2 - v_1}{\triangle t} = \frac{27 - 0 }{2.7} = 10 \ \frac{m}{s^2}$$

قسمت ۲: مقدار جابجایی اتومبیل در فاصله زمانی داده شده، به صورت زیر به‌دست می‌آید:

$$\triangle x = \frac{1}{2} at^2 + v_0 t \\ = \frac{1}{2} (10) (2.7)^2 + (0)(2.7) \\ = 36.45 \ m$$

قسمت ۳: در این قسمت، مقدار کار انجام شده بر روی اتومبیل محاسبه خواهد شد. برای محاسبه کار از قضیه کار و انرژی استفاده می‌کنیم.

$$W_{net} = \triangle K \\= \frac{1}{2}m (v_2^2 - v_1^2) \\ = \frac{1}{2} (1650 \ kg) ((27 \ \frac{m}{s})^2 - (0 \ \frac{m}{s})^2)\\ = 601425 \ J$$

قسمت ۴: در قسمت ۲، مسافت طی شده توسط اتومبیل حساب شد و مقدار ۳۶/۴۵ متر به‌دست آمد. در قسمت ۳، مقدار کار کل انجام شده محاسبه شد. در نتیجه، با استفاده از فرمول کار، یعنی W=Fd، مقدار نیروی متوسط وارد شده بر اتومبیل را به‌دست می‌آوریم:

$$F = \frac{W}{ d}= \frac{601425}{36.45} = 16500 \ N$$

مثال ۴

کامیونی به جرم ۱۲۰۰۰ کیلوگرم با سرعت ثابت ۱۲۶ کیلومتر بر ساعت حرکت می‌کند. ناگهان راننده مانعی را می‌بیند و به سرعت ترمز می‌کند و پس از طی مسافت ۱۲ متر می‌ایستد. چه مقدار کار بر روی کامیون انجام شده است؟

پاسخ: کار کل انجام شده بر روی کامیون برابر با کار انجام شده توسط نیروی اصطکاک بین لاستیک کامیون و جاده و کار انجام شده توسط ترمزها برای نگه داشتن آن است.

به منظور به‌دست آوردن کار کل، نیازی به دانستن بزرگی این نیروهای پیچیده نیست، بلکه تنها با دانستن سرعت‌های اولیه و نهایی کامیون و استفاده از قضیه کار و انرژی، می‌توانیم مقدار کار انجام شده بر روی کامیون را به‌دست آوریم.

در ابتدا، سرعت‌ها را از کیلومتر بر ساعت به متر بر ثانیه تبدیل می‌کنیم:

$$126 \ \frac{km}{h} \times \frac{10}{36} = 35 \ \frac{m}{s}$$

اکنون، با استفاده از قضیه کار و انرژی مقدار کار انجام شده را به‌دست می‌آوریم:

$$W_{net} = \triangle K \\ = \frac{1}{2}m v_2^2 - \frac{1}{2}m v_1^2 \\ = \frac{1}{2} (1200) (0)^2 - \frac{1}{2} (1200)(35)^2 \\ = 735 \ kJ$$

مثال ۵

اتوبوسی به وزن ۴۶۰۰ کیلوگرم با سرعت ۲۶/۵ متر بر ثانیه حرکت می‌کند. اگر اتوبوس ناگهان ترمز کند و پس از طی مسافت ۴۶ متر بایستد، مقدار نیرویی که توسط ترمزها بر آن وارد می‌شود را به‌دست آورید.

پاسخ: برای حل این مثال، دو راه حل وجود دارد:

1. استفاده از قضیه کار و انرژی
2. استفاده از قانون دوم نیوتن.

تمام اطلاعات لازم برای استفاده از قضیه کار و انرژی داده شده است. بنابراین، داریم:

$$W_{net} = \triangle K \\ = \frac{1}{2}m v_2^2 - \frac{1}{2}m v_1^2 \\ = \frac{1}{2} (4600) (0)^2 - \frac{1}{2} (4600)(26.5)^2 \\ = 1615175 \ kJ$$

مقدار به‌دست آمده برابر کار انجام شده توسط تمام نیروها، بر روی اتوبوس است. برای به‌دست آوردن بزرگی نیروی کل، از تعریف کار استفاده می‌کنیم:

$$W = Fd \rightarrow F = \frac{W}{d} = \frac{1615157}{46}= 35112.5 \ N$$

برای حل این مثال می‌توانیم از رابطه‌های حرکت بر خط راست با شتاب ثابت نیز استفاده کنیم. با استفاده از معادله مستقل از زمان حرکت با شتاب ثابت داریم:

$$v^2 - v_0^2 = 2a\triangle x \\ a = \frac{v^2 - v_0^2}{2 a \triangle x} \\ = \frac{0 - (26.5)^2}{2\times 46}= 7.633 \ \frac{m}{s^2}$$

از قانون دوم نیوتن برای به‌دست آوردن بزرگی نیرو استفاده می‌کنیم:

$$F = ma = (4600 \ kg)\times (7.633) = 35112.5$$

مثال ۶

جعبه‌ای به جرم ۲ کیلوگرم با نیروی ثابتی برابر ۵۰ نیوتن بر روی سطح لغزنده‌ای کشیده می‌شود. اگر جعبه از حالت سکون شروع به حرکت کرده باشد، انرژی جنبشی آن پس از طی چه مسافتی برابر ۳۸۰ ژول می‌شود؟

پاسخ: سرعت اولیه و در نتیجه انرژی جنبشی اولیه جعبه برابر صفر است. با استفاده از قضیه کار و انرژی، مقدار کار انجام شده بر روی جعبه را به‌دست می‌آوریم:

$$W_{net} = \triangle K = K_2- K_1 = 380 \ J$$

اگر فرض کنیم که تمام نیروهای وارد شده بر جعبه ثابت و موازی جابجایی آن باشند، فرمول $$W_{net} = Fd$$ مقدار جابجایی را می‌دهد:

$$d = \frac{W_{net}}{F} = \frac{380 }{50 } = 7.6 \ m$$

مثال ۷

جسمی به جرم ۲ کیلوگرم مطابق تصویر نشان داده شده در ادامه توسط نیروی برابر ۶۶ نیوتن از حالت سکون، شروع به حرکت می‌کند. جسم بر روی سطح زبر و به اندازه ده متر جابجا می‌شود. اگر مقدار متوسط نیروی اصطکاک برابر ۲۵ نیوتن باشد، سرعت جسم در انتهای مسیر را به‌دست آورید.

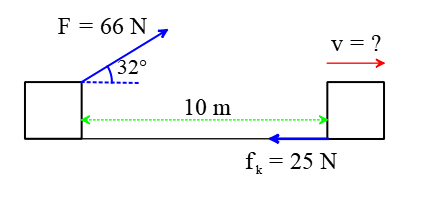
پاسخ: این مثال را با استفاده از قضیه کار و انرژی حل می‌کنیم. برای استفاده از این اصل، نیاز به دانستن مقدار نیروی کل وارد شده بر جسم و سرعت‌های اولیه و نهایی آن داریم. در ابتدا، نمودار آزاد جسم را رسم می‌کنیم و تمام نیروهای وارد شده بر آن را نشان می‌دهیم. همان گونه که در تصویر فوق نشان داده شده است، دو نیرو بر جسم وارد می‌شوند:

1. مولفه موازی سطحِ نیروی وارد شده بر جسم.
2. نیروی اصطکاک که در خلاف جهت جسم بر آن وارد می‌شود.

دو نیرو در خلاف جهت یکدیگر قرار دارند، بنابراین نیروی کل برابر است با:

$$F_{tot} = F_{\parallel} - f_k \\ = F cos \alpha - f_k \\ = 66\ cos 32^o - 25 \\ = 31.1 \ N$$

از اصل کار و انرژی داریم:

$$\triangle K = W_{net} \\ K_2 - K_1 = F_{tot} d \\ K_2 - 0 = 31.1 \times 10 \\ \Rightarrow K_2 = 311 \ J$$

مقدار انرژی جنبشی در انتهای مسیر را به‌دست آوردیم. برای محاسبه سرعت در انتهای مسیر از رابطه انرژی جنبشی استفاده می‌کنیم:

$$K = \frac{1}{2}m v^2 \\ v = \sqrt{\frac{2K}{m}} = \sqrt{\frac{2 \times 311}{2}} = 17.6 \ \frac{m}{s}$$

پس از پاسخ به پرسش کار چیست و آشنایی با قضیه کار و انرژی، در مورد رابطه میان انرژی پتانسیل و کار صحبت می‌کنیم.

انرژی پتانسیل و کار

در مطالب فوق به پرسش کار چیست پاسخ دادیم. همچنین، در مورد رابطه بین کار و انرژی جنبشی صحبت کردیم. انرژی پتانسیل نیز با کار رابطه دارد. انرژی پتانسیل، U، برابر مقدار کاری است که برای جابجایی جسم از نقطه مرجع با انرژی پتانسیل صفر به نقطه‌ای با موقعیت r، انجام می‌شود. نقطه مرجع یک نقطه دلخواه است، بنابراین با توجه به مساله داده شده انتخاب می‌شود.

نیروی وارد شده بر جسمی دلخواه برابر منفی مشتق تابع انرژی پتانسیل است. به بیان دیگر، منفی شیب نمودار انرژی پتانسیل برابر نیرو خواهد بود. رسم نمودار انرژی پتانسیل کمک زیادی به درک بهتر تغییرات نیرو در ناحیه مشخصی از فضا می‌کند.

$$U = -\int_{ref}^{r} \overrightarrow{F}. d \overrightarrow{r} \\ F(x) = - \frac{\text{d}U}{\text{d}x}$$

چرا در رابطه‌های فوق از علامت منفی استفاده شده است؟

گفتیم انرژی پتانسیل برابر مقداری کاری است که باید برخلاف نیرو، انجام شود تا جسمی از نقطه مرجع به نقطه‌ای با پتانسیل U، منتقل شود. نیرویی که برای جابجایی جسم وارد می‌کنیم برابر ولی در خلاف جهت حرکت است و این دلیل گذاشتن علامت منفی در رابطه‌های فوق است. علامت منفی در مشتق انرژی پتانسیل نشان می‌دهد که اگر پتانسیل U با افزایش r، افزایش یابد، نیرو تمایل به حرکت جسم به سمت rهای کمتر برای کاهش انرژی پتانسیل دارد.

نیروهای پایستار

در تعریف کار چیست بیان کردیم که اگر نیرویی بر جسمی وارد شود و جسم به ‌اندازه معینی در راستای نیروی وارد شده جابجا شود، مقدار کار انجام شده بر روی آن برابر $$W=Fd$$ خواهد بود. جسم جابجا می‌شود و برای جابجا شدن، مسیر مشخصی را طی می‌کند. مسیرهای مختلفی توسط جسم طی می‌شود، آیا مقدار کار انجام شده به این مسیرها بستگی خواهد داشت؟ با توجه به اینکه کار انجام شده به مسیر بستگی داشته باشد یا خیر، دو نوع نیرو تعریف می‌شود:

1. نیروهای پایستار
2. نیروهای ناپایستار

نیروی پایستار نیرویی است که کار کل انجام شده برای جابجایی ذره‌ای از نقطه ‌A به B، مستقل از مسیر پیموده شده باشد. مفهوم مستقل در این تعریف به دلیل آن است که ذره می‌تواند از مسیر ۱ از نقطه A به B برود و از مسیر متفاوت ۲ به نقطه A برگردد. در این تغییر مسیر هیچ اتلاف انرژی نداریم.

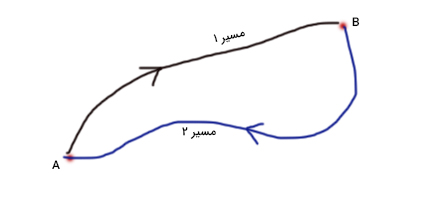
کار انجام شده توسط نیروهای پایستار مستقل از مسیر است. به بیان دیگر، کار انجام شده توسط نیروی پایستار برای هر دو مسیر متصل‌کننده نقطه‌های اولیه و پایانی، یکسان است:

$$W_{AB, path-1} = \int_{AB, path-1} \overrightarrow{F}_{cons} d\overrightarrow{r} = W_{AB, path-2} = \int_{AB, path-2} \overrightarrow{F}_{cons} d\overrightarrow{r}$$

کار انجام شده توسط نیروی ناپایستار به مسیر طی شده وابسته است.

به طور معادل، کار انجام شده توسط نیروی پایستار در هر مسیر بسته‌ای برابر صفر است:

$$W_{closed path} = \oint \overrightarrow{F}_{cons} d\overrightarrow{r} = 0$$

در رابطه فوق از علامت دایره در وسط انتگرال استفاده شده است. این علامت برای انتگرال بر روی مسیر بسته و در بسیاری از کتاب‌های فیزیک و ریاضی استفاده می‌شود. هر مسیر بسته‌ای برابر جمع دو مسیر است:

• مسیر ۱ از A به ‌B
• مسیر ۲ از B به A

کار انجام شده برای رفتن از B به A برابر منفی کار انجام شده برای رفتن از A به B است. A و B هر دو نقطه‌ای بر روی مسیر بسته هستند.

$$0 = \int \overrightarrow{F}_{cons} d\overrightarrow{r} = \int_{AB, path-1} \overrightarrow{F}_{cons} d \overrightarrow{r} + \int_{BA, path-2} \overrightarrow{F}_{cons} d \overrightarrow{r} \\ = \int_{AB, path-1} \overrightarrow{F}_{cons} d \overrightarrow{r} - \int_{AB, path-2} \overrightarrow{F}_{cons} d \overrightarrow{r} = 0$$

اگر F نیرویی پایستار و W کار انجام شده بر روی جسم توسط نیروی F باشد، داریم:

$$\triangle U = -W \\ \int dU = - \int \overrightarrow{F}. d\overrightarrow{r} \\ \int dU = \int - \overrightarrow{F}. d\overrightarrow{r} \\ dU = - \overrightarrow{F}. d\overrightarrow{r}$$

ضرب داخلی فوق را برای مولفه‌های مختلف نیرو و جابجایی انجام می‌دهیم:

$$dU = - \overrightarrow{F}. d\overrightarrow{r} = -F_xdx - F_y dy - F_z dz$$

dU را نیز به صورت زیر می‌نویسیم:

$$dU = \frac{\partial U}{\partial x} dx + \frac{\partial U}{\partial y} dy + \frac{\partial U}{\partial z} dz$$

در نتیجه، برای مولفه نیروی F در راستای محور x داریم:

$$F_x = - \frac{\partial U}{\partial x}$$

مشخصه‌های کلی نیروی پایستار به صورت زیر خلاصه می‌شوند:

• نیرو تنها به نقطه‌های اولیه و پایانی بستگی و مستقل از مسیر طی شده است.
• در هر مسیر بسته‌ای، مقدار کار انجام شده برابر صفر است.
• کار انجام شده توسط نیروی پایستار، برگشت‌پذیر است.

سوالی که ممکن است مطرح شود آن است که اگر نیروی درگیر، پایستار نباشد چه اتفاقی رخ خواهد داد؟ آیا پاسخ پرسش کار چیست تغییر می‌کند؟

نیروهای ناپایستار

نیروی ناپایستار نیرویی است که کار آن به مسیر طی شده توسط ذره بستگی دارد. نیرویی ناپایستار است که انرژی مکانیکی را تغییر دهد. کار انجام شده توسط نیروهای ناپایستار سبب کم شدن یا اضافه شدن مقدار انرژی مکانیکی می‌شود. به عنوان مثال، هنگامی که نیروی اصطکاک کار انجام دهد، انرژی به صورت گرما تلف می‌شود.

مشخصه‌های نیروهای ناپایستار عبارت هستند از:

• به مسیر طی شده و در نتیجه نقطه‌های اولیه و نهایی وابسته است.
• در هر مسیر بسته، کار کل انجام شده توسط نیروی ناپایستار صفر نیست.
• کار انجام شده توسط نیروی ناپایستار برگشت‌ناپذیر است.

برای درک بهتر پرسش کار چیست و کار انجام شده توسط نیروهای ناپایستار، دو مثال در این مورد حل می‌شوند.

مثال اول کار نیروی ناپایستار

ضریب اصطکاک بین جسمی به جرم ۳/۰ کیلوگرم و سطح برابر ۰/۴ است. سیستم از حالت سکون شروع به حرکت می‌کند. سرعت جسم آویزان به جرم ۵/۰ کیلوگرم پس از ۱/۵ متر سقوط را به‌دست آورید.

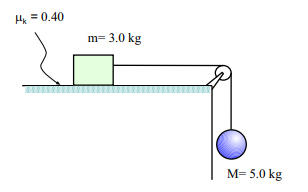
پاسخ: هنگامی که سیستم نشان داده شده در شکل فوق شروع به حرکت می‌کند، دو جرم شتاب می‌گیرند، زیرا هر دوی آن‌ها توسط طناب نازکی به یکدیگر متصل شده‌اند. جرم m بر روس سطح زبری حرکت می‌کند و نیروی اصطکاک بر روی آن کار انجام می‌دهد. از آنجایی که ارتفاع آن ثابت است، انرژی پتانسیل آن تغییر نخواهد کرد، اما انرژی جنبشی آن افزایش می‌یابد. جرم آویزان M، آزادانه به طرف پایین حرکت می‌کند. انرژی پتانسیل آن کاهش ولی انرژی جنبشی آن افزایش می‌یابد.

برای حل این مثال از اصل‌های انرژی استفاده خواهیم کرد. از آنجایی که نیروی اصطکاک بر جرم قرار داده شده بر روی میز، وارد می‌شود، باید کار انجام شده توسط آن را به‌دست آوریم. نیروهای وارد شده بر جرم m در شکل زیر نشان داده شده‌اند:

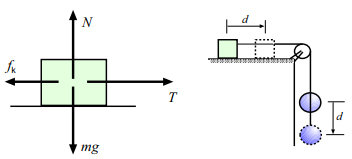
نیروی عمودی سطح برابر نیروی وزن است. بنابراین، فرمول نیروی اصطکاک جنبشی بر روی جرم m برابر $$\mu_k N = \mu_k m g$$ است. این نیرو در خلاف جهت حرکت جسم بر آن وارد می‌شود. کار انجام شده توسط این نیرو برابر است با:

$$W_{fric} = f_k d\ cos\phi = (\mu_k mg) (d) (-1) = - (0.4)(3.0 \ kg) (9.80 \ \frac{m}{s^2} (1.5 \ m) = -\ 17.6 \ J$$

زاویه بین نیروی اصطکاک و جابجایی برابر ۱۸۰ درجه است.

سرعت اولیه جرم m برابر صفر و سرعت نهایی آن برابر v است. بنابراین، برای تغییرات انرژی جنبشی داریم:

$$\triangle K = \frac{1}{2}(3.0 \ kg) v^2 - 0 = (1.5 \ kg) \ v^2$$

همان گونه که گفتیم، تغییرات انرژی پتانسیل جرم m برابر صفر است.

تغییرات انرژی پتانسیل جرم M برابر است با:

$$\triangle K = \frac{1}{2}(5.0 \ kg) v^2 - 0 = (2.5 \ kg) \ v^2$$

جرم M از طناب آویزان است، بنابراین ارتفاع آن نیز تغییر خواهد کرد. این جرم به اندازه d- به‌سمت پایین حرکت می‌کند. در نتیجه، تغییرات انرژی پتانسیل جاذبه آن برابر است با:

$$\triangle U = Mg\triangle y = (5.0 \ kg) (9 .80 \ \frac{m}{s^2}) (-1.5 \ m) = -73.5 \ J$$

برای به‌دست آوردن تغییرات کل انرژی مکانیکی سیستم، تغییرات انرژی دو جرم را با یکدیگر جمع می‌کنیم:

$$\triangle E = (1.5 \ kg) v^2 + (2.5 \ kg) v^2 - 73.5 \ J \\ = (4.0 \ kg) v^2 - 73.5 \ J$$

با استفاده از رابطه $$\triangle E = W_{fric}$$ داریم:

$$(4.0 \ kg) v^2 - 73.5 \ J =-17.6 \ J$$

رابطه فوق را بر حسب v حل می‌کنیم:

$$(4.0 \ kg) v^2 = 55.9 \ J \Rightarrow v^2 = \frac{55.9 \ J}{4.0 \ kg} = 14.0 \ \frac{m^2}{s^2} \\ v = 3.74 \ \frac{m}{s}$$

مثال دوم کار نیروی ناپایستار

جسمی به جرم ۲/۰ کیلوگرم از حالت سکون از نقطه A رها می‌شود (تصویر نشان داده شده در ادامه). مسیر حرکت ذره، به جز در قسمت BC به طول ۶/۰۰ متر، بدون اصطکاک است. جسم پس از پایین آمدن از ارتفاع ۳/۰۰ متری و گذشتن از قسمت BC، به فنری با ثابت فنر ۲۲۵۰ نیوتن بر متر برخورد می‌کند و آن را به اندازه ۰/۳۰۰ متر فشرده می‌کند. ضریب اصطکاک جنبشی بین سطح BC و جسم را به‌دست آورید.

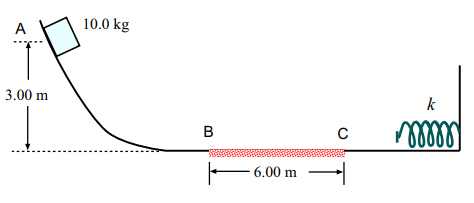
پاسخ: برای حل این مثال از روش‌های انرژی استفاده می‌کنیم. نیروهای وارد شده بر جرم از سقوط آن تا فشردن فنر عبارت هستند از:

• نیروی جاذبه
• نیروی فنر
• نیروی اصطکاک هنگامی‌ که از مسیر زبر می‌گذرد.

نیروهای جاذبه (گرانش) و نیروی وارد شده از طرف فنر، نیروهای پایستار هستند. اما نیروی اصطکاک نیروی ناپایستار است. هنگامی‌که نیروها ناپایستار هستند، داریم:

$$\triangle K + \triangle U = W_{non-cons}$$

برای به‌دست آوردن ضریب اصطکاک ایستایی، از رابطه فوق استفاده می‌کنیم. در این رابطه، مقدار تغییرات انرژی‌های جنبشی و پتانسیل به ‌آسانی محاسبه می‌شوند.

جسم از نقطه A رها می‌شود، بنابراین سرعت و مقدار انرژی جنبشی اولیه آن برابر صفر خواهد بود. جسم از ارتفاع ۳/۰۰ متری سطح زمین رها شده است، در نتیجه مقدار انرژی پتانسیل آن برابر است با:

$$U_i = mg h = (10.0 \ kg) (9.80 \ \frac{m}{s^2}) (0.300 \ m) ^2 = 1.01 \times 10^2 \ J$$

جسم پس از پایین آمدن و حرکت بر روی سطح زبر، فنر را فشرده می‌کند. زمانی را در نظر می‌گیریم که فنر به حداکثر فشردگی خود توسط جسم رسیده است، در این حالت جسم ساکن و سرعت آن برابر صفر خواهد بود.

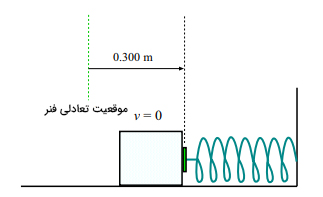
در اینجا، تنها به نقطه‌های ابتدایی و انتهایی مسیر حرکت توجه می‌کنیم، این‌که جسم با چه سرعتی حرکت یا به فنر برخورد کرده است، مهم نیست.

در نقطه پایانی (فشردگی حداکثر فنر)، جسم در حالت سکون قرار دارد، بنابراین سرعت و انرژی جنبشی آن برابر صفر است. همچنین، جسم بر روی زمین و در ارتفاع صفر از آن قرار گرفته است، بنابراین مقدار انرژی پتانسیل جاذبه برابر صفر خواهد بود. اما، جسم سبب فشردگی فنر شده است و باید مقدار انرژی پتانسیل ذخیره شده در فنر را به‌دست آوریم:

$$U_{spring} = \frac{1}{2}k x^2 = \frac{1}{2}(2250 \ \frac{N}{m}) ( 0.300 \ m)^2 = 1.01 \times 10^2 \ J$$

بنابراین، مقدار انرژی پتانسیل نهایی برابر با $$1.01 \times 10^2$$ است.

مقدار انرژی مکانیکی کل سیستم تغییر خواهد کرد، زیرا نیروی ناپایستار اصطکاک بر روی جسم کار انجام می‌دهد. هنگامی‌ که جسم بر روی سطح زبر حرکت می‌کند، نیروهای عمودی وارد شده بر جسم، نیروهای وزن و نیروی عمودی سطح هستند. از آنجایی که جسم موردنظر در راستای عمودی حرکتی انجام نمی‌دهد، برآیند این دو نیرو برابر صفر است:

N = mg

بزرگی نیروی اصطکاک برابر است با:

$$f_k = \mu_k N = \mu_k mg = \mu_k (10.0 \ kg) (9.80 \ \frac{m}{s^2}) = \mu_k (98.0 \ N)$$

طول مسیر زبر و دارای اصطکاک برابر ۶/۰۰ متر است و نیروی اصطکاک در خلاف جهت حرکت جسم بر آن وارد می‌شود. بنابراین، کار انجام شده توسط این نیرو بر روی جسم برابر است با:

$$W_{fric} = f_kd \ cos\phi = \mu_k (98.0 \ N) (6.00 \ m) cos 180^o = - \ \mu_k (5.88 \times 10^2 \ J)$$

برای به‌دست آوردن ضریب اصطکاک ایستایی، تمام داده‌های موردنظر را به‌دست آورده‌ایم:

$$(0 - 0) + (1.01 \times 10^2 \ J - 2.94 \times 10^2 \ J) =- \mu_k (5.88 \times 10^2 \ J) \\ -1.93 \times 10^2 \ J = - \mu_k (5.88 \times 10^2 \ J)\Rightarrow \mu_k = 0.328$$

اکنون می‌توانید به خوبی به پرسش کار چیست پاسخ دهید. با نیروهای پایستار و ناپایستار و تفاوت بین آن‌ها آشنا شدید. در ادامه، در مورد کار انجام شده توسط نیروهای متغیر، نیروی گرانش و نیروی فنر آشنا می‌شویم.

کار انجام شده توسط نیروی متغیر

تاکنون پرسش کار چیست را تنها برای نیروهای ثابت پاسخ دادیم. در ادامه، در مورد کار انجام شده توسط نیروهای متغیر صحبت خواهیم کرد. ابتدا در مورد نیروهای متغیر و ثابت صحبت می‌کنیم. کار انجام شده توسط نیرو می‌تواند به کار انجام شده توسط نیروی ثابت و متغیر تقسیم شود. نیرو هنگامی ثابت است که جهت و اندازه آن با گذشت زمان ثابت باقی بماند. در این حالت، کار برابر حاصل‌ضرب نیروی وارد شده در مقدار جابجایی جسم است (زاویه بین نیرو و جابجایی مهم است).

کار انجام شده توسط نیروی متغیر کمی پیچیده است. در این حالت، بزرگی و جهت نیرو با گذشت زمان تغییر می‌کند. بیشتر کارهای انجام شده در زندگی روزمره مثال‌هایی از کار نیروی متغیر هستند. برای محاسبه کار توسط نیروی متغیر، نیاز به حل انتگرال داریم.

همان‌ گونه که می‌دانیم، نیرو هنگامی بر روی سیستمی کار انجام می‌دهد که سیستم در راستای نیروی اعمال شده جابجا شود. کار انجام شده توسط نیروی ثابتی با بزرگی F که ذره‌ای را به ‌اندازه $$\triangle x$$ جابجا می‌کند برابر است با:

$$W = F \triangle x$$

زمانی که نیرو متغیر است، کار با استفاده از انتگرال محاسبه می‌شود. به عنوان مثال، جسم متصل به فنری افقی را در نظر بگیرید. مقدار نیروی وارد شده از طرف فنر برابر است با:

$$F_s = -k x$$

در رابطه فوق:

• k ثابت فنر است.
• x جابجایی جسم متصل به فنر است.

همان گونه که مشخص است نیرو متناسب با جابجایی جسم از مکان تعادل است. نیروی وارد شده بر جسم با تغییر مکان آن نسبت به حالت تعادل، تغییر می‌کند. بنابراین، برای به دست آوردن کار کل، سهم بی‌نهایت کوچک از کار انجام شده در هر لحظه محاسبه و با یکدیگر جمع می‌شوند. کار انجام شده توسط فنر عبارت است از:

$$W_s = \int F(x) dx = \int_{x_i}^{x_f} k dx = \frac{1}{2}k \triangle x^2$$

نمودار نیرو - جابجایی

به نمودار داد شده نیرو بر حسب جابجایی دقت کنید.

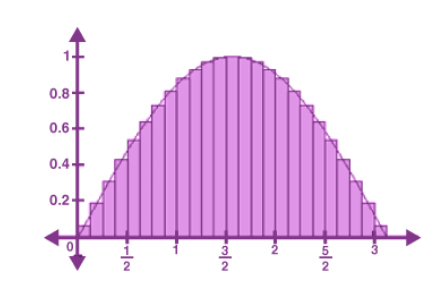
سطح زیر نمودار به فاصله‌های کوچک و مساوی برابر $$\triangle x$$ تقسیم شده است. فرض می‌کنیم $$\triangle x$$ بسیار کوچک است. در این صورت، می‌توان نیروی اعمال شده در جابجایی $$\triangle x$$ را ثابت در نظر گرفت. هر قسمت تقسیم شده مستطیلی با طولی برابر بزرگی نیروی F(x) و عرضی برابر جابجایی $$\triangle x$$ است، در نتیجه، مقدار کار انجام شده برای هر قسمت برابر است با:

$$\triangle W = F(x) \triangle x$$

مقدار کار کل برابر جمع کار انجام شده در هر قسمت است:

$$W = \sum_{x_i}^{x_f} F(x) \triangle x$$

فرض می‌کنیم که جابجایی هر قسمت به صفر نزدیک می‌شود، در نتیجه تعداد مستطیل‌های زیر نمودار به سمت بی‌نهایت میل می‌کند و جمع به انتگرال تبدیل می‌شود:

$$W = \lim_{x \rightarrow 0}\sum_{x_i}^{x_f} F(x) \triangle x \\ W = \int_{x_i}^{x_f} F(x)dx$$

بنابراین، کار انجام شده توسط نیروی متغیر به صورت انتگرال معین نیرو در جابجایی سیستم، محاسبه می‌شود.

نمونه سوال کار نیروی متغیر

برای درک بهتر کار انجام شده توسط نیروی متغیر، مثال‌هایی در این مورد حل می‌شوند.

مثال ۱

اگر نیرویی برابر $$\overrightarrow{F} = 30 \overrightarrow{i} + 5\overrightarrow{j}$$ سبب جابجایی ذره‌ای به اندازه $$\overrightarrow{r} = 5 \overrightarrow{i} + 2 \overrightarrow{j}$$ شود، مقدار کار انجام شده را به‌دست اورید.

پاسخ: کار انجام شده توسط نیروی ثابت به صورت زیر به‌دست می‌آید:

$$W = \overrightarrow{F}. \overrightarrow{r}$$

با جایگذاری نیرو و جابجایی در رابطه فوق داریم:

$$W = (30 \overrightarrow{i} + 5 \overrightarrow{j}). ( 5 \overrightarrow{i} + 2 \overrightarrow{j} ) \\ W = (30)(50) + (5)(2) \\ W = 150 + 10 \\ W = 160 \ J$$

مثال ۲

اگر مقدار نیروی اعمال شده بر ذره‌ای برابر $$F=x$$ باشد و آن را به اندازه ۴ متر جابجا کند، بزرگی کار انجام شده توسط این نیرو را به‌‌دست آورید.

پاسخ: کار انجام شده توسط نیروی متغیر به صورت زیر به‌دست می‌آید:

$$W = \int_{x_i}^{x_f} F dx$$

نیرو را در رابطه فوق قرار می‌دهیم:

$$W = \int_{x_i}^{x_f} F dx \\ W = \int_{0}^{x} F dx \\ = \int_{0}^{x} x dx \\ = |\frac{x^2}{2} |_0^2 \\ W = \frac{x^2}{2}$$

در اینجا، مقدار جابجایی یعنی x برابر ۴ متر است. در نتیجه، مقدار کار برابر است با:

$$W = 8 \ J$$

مثال ۳

اگر نیروی نوسانی به صورت $$F(x) = sinx$$ بر ذره‌ای وارد شود و آن را از مکان x= -1 به x=1 ببرد، مقدار کار انجام شده در این جابجایی را به‌دست آورید.

پاسخ: کار انجام شده توسط نیروی متغیر برابر است با:

$$W = \int_{x_i}^{x_f} F dx$$

با جایگذاری نیرو در رابطه بالا داریم:

$$W = \int_{x_i}^{x_f} F dx \\ W = \int_{-1}^{1} F dx \\ = \int_{-1}^{1} sinx dx \\ = |-cos(x) |_{-1}^1 \\ W = \cos (-1) - cos (1) = 0$$

مثال ۴

نیروی متغیری بر جسمی به جرم ۲ کیلوگرم در راستای محور x وارد می‌شود. نیرو به صورت تابع زیر بر حسب x تغییر می‌کند:

$$F_x = (3+0.2x) \ N$$

مقدار کار انجام شده توسط این نیرو را در جابجایی جسم از مکان صفر تا ۵ متر به‌دست آورید.

پاسخ: مقدار کار انجام شده در این جابجایی به صورت زیر محاسبه می‌شود:

$$W = \int_{x_a}^{x_b}Fdx \\ W = \int_{0}^{5} (3 + 0.2x)dx = 17.5 \ J$$

مثال ۴

نیروی متغیری مطابق تصویر زیر و در راستای محور x بر جسمی وارد می‌شود، مطلوب است:

1. کار انجام شده در فاصله x=0 تا x=5 متر.
2. کار انجام شده در فاصله x=5 تا x=10 متر.
3. کار انجام شده در فاصله x=10 تا x=15 متر.

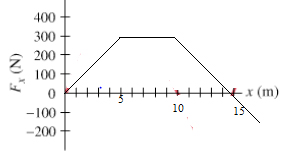
پاسخ: کار انجام شده در هر ناحیه برابر با مساحت زیر نمودار در آن ناحیه است:

قسمت ۱: کار انجام شده در فاصله x=0 تا x=5 متر برابر است با:

$$W = \frac{1}{2} \times 300 \times 5 = 750 \ N$$

قسمت ۲: کار انجام شده در فاصله x=5 تا x=10 متر برابر است با:

$$W = 300 \times 5 =1500 \ N$$

قسمت ۳: کار انجام شده در فاصله x=10 تا x=15 متر برابر است با:

$$W = \frac{1}{2} \times 300 \times 5 = 750 \ N$$

مثال ۵

مردی کامیونی را با نیرویی برابر ۱۰۰ نیوتن بر روی سطح زبری به اندازه ۱۰ متر می‌کشاند. مرد خسته می‌شود، بنابراین مقدار نیروی وارد شده بر کامیون را به صورت خطی با مکان تا مقدار ۵۰ نیوتن کاهش می‌دهد. مسیر کل طی شده توسط کامیون برابر ۲۰ متر است.

1. نمودار نیروی اعمال شده توسط مرد را بر حسب مکان رسم کنید.
2. مقدار کار انجام شده را در فاصله ۲۰ متری به‌دست آورید.
3. مقدار کار انجام شده توسط نیروی اصطکاک در فاصله ۲۰ متری را به‌دست آورید.
4. مقدار کار کل انجام شده را به‌دست آورید.

پاسخ:

قسمت ۱: نمودار نیروی اعمال شده از طرف مرد و نیروی اصطکاک (۵۰ نیوتن) به صورت زیر رسم شده است:

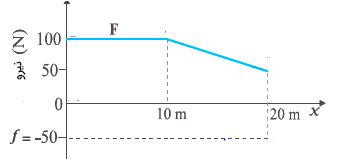
نیروی اصطکاک ثابت و در خلاف جهت نیروی اعمال شده است.

قسمت ۲: کار انجام شده توسط مرد با مساحت زیر نمودار به‌دست می‌آید. نمودار از دو قسمت تشکیل شده است. تا مکان ۱۰ متر، نیروی وارد شده از طرف مرد ثابت و برابر ۱۰۰ نیوتن است. در نتیجه، مساحت زیر نمودار این قسمت برابر مساحت مستطیلی به عرض ۱۰۰ نیوتن و طول ۱۰ متر است. از مکان ۱۰ تا ۲۰ متر، نیروی وارد شده به صورت خطی تا مقدار ۵۰ نیوتن کاهش می‌یابد. بنابراین، مساحت این قسمت برابر مساحت ذوزنقه‌ای به ارتفاع ۱۰ متر خواهد بود.

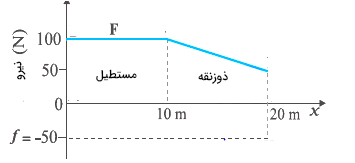
کار کل انجام شده در جابجایی ۲۰ متر برابر است با:

$$W = 100 \times 10 + \frac{1}{2}(100 + 50) \times 10 \\ = 1000 + 750 \\ = 1750 \ J$$

قسمت ۳: کار انجام شده توسط نیروی اصطکاک برابر مساحت زیر نمودار است (مستطیل):

$$W = -50 \times 20 = -1000 \ J$$

قسمت ۴: مقدار کار کل انجام شده بر روی کامیون برابر جمع جبری کار انجام شده توسط مرد و کار انجام شده توسط نیروی اصطکاک است:

$$W = -50 \times 20 = -1000 \ J$$

مثال ۶

مخزن آب مخروطی شکلی با ارتفاع ۸ متر و قطر ۶ متر در گوشه حیاط ساختمانی قرار دارد. تمام محتویات داخل تانک باید به بالای آن منتقل شود. اگر مخزن تا ارتفاع ۴ متری پر شده باشد، مقدار کار لازم را به‌دست آورید.

پاسخ: آب تا ارتفاع ۴ متری مخزن پر شده است، این فاصله را به فاصله‌های بسیار کوچک تقسیم می‌کنیم:

$$0 = x_0 < x_1< x_2 ...< x_{n-1} < x_n= 4$$

$$T = t_1 \leq t_2 \leq ...\leq t_n$$

کار $$W_i$$ برای پمپاژ آب بین فاصله‌های $$x_{i-1}$$ و $$x_{i}$$ به طور تقریب برابر حاصل‌ضرب نیروی $$F_i$$ لازم برای بالا بردن آب در فاصله $$d_i = 8 - t_i$$ (فاصله‌ای که باید بالا برده شود) است. حجم آبی که بین سطح‌های $$x_{i-1}$$ و $$x_{i}$$ قرار گرفته است به طور تقریب برابر حجم دیسکی با شعاع $$r_i= (8 - t_i)\frac{3}{8}$$ و ضخامت $$\triangle x_i = x_i - x_{i-1}$$ است. حجم این قسمت برابر است با:

$$V_i = \pi r_i^2\triangle x_i= \frac{9 \pi}{64}(8-t_i)^2\triangle x_i$$

جرم $$M_i$$ این حجم آب برابر است با:

$$M_i = 1000 \ kg \times V_i = 1000 \times \frac{9 \pi}{64}(8 - t_i)^2 \triangle x_i \ kg$$

نیروی $$F_i$$ لازم برای بلند کردن آب برابر است با:

$$F_i = 9.8 M_i = 9800 \times \frac{9 \pi}{64}(8 - t_i)^2 \triangle x_i \ N$$

بنابراین، مقدار کار $$ٌW_i$$ برای بلند کردن جرم به بالای مخزن آب به طور تقریب با استفاده از رابطه زیر به‌دست می‌آید:

$$F_i d_i= 9800 \times \frac{9 \pi}{64}(8 - t_i)^2 \triangle x_i \ N \times (8 - t_i) = 9800 \pi (8-t_i)^3 \times \frac{9}{64}\triangle x_i$$

با جمع بستن تمام $$W_i$$ها، کار کل به‌دست خواهد آمد:

$$W_i = \sum_{i=1}^n \ 9800 \ (8-t_i)^3 \times \frac{9\pi}{64}\triangle x_i$$

 اگر هر یک از تقسیم‌بندی‌ها را بسیار کوچک کنیم، داریم:

$$W_i = \lim_{|ُT| \rightarrow 0}\sum_{i=1}^n F_id_i = \sum_{i=1}^n \ 9800 \ (8-t_i)^3 \times \frac{9\pi}{64}\triangle x_i \\ W = 9800 \ \frac{9 \pi}{64} \int_{x=0}^{x=4} (8-x)^3 dx$$

برای حل انتگرال فوق، از روش جایگزینی استفاده می‌کنیم:

$$u= 8-x \Rightarrow dx = -du$$

اگر x=0 باشد مقدار u برابر ۸ , و اگر x=4 باشد مقدار u برابر ۴ خواهد بود. بنابراین، داریم:

$$9800\times \frac{9 \pi}{64}\int_{x = 0}^{x = 4} (8-x)^ 3 dx = -9800 \times \frac{9 \pi}{64}\int_{u= 8}^{u = 4 } u^3 du = -9800 \frac{9 \pi}{64} \frac{u^4}{4}| _{u=8}^{u=4}\\ = -9800 \times \frac{9 \pi}{4(64)} 4^4 (1^4 - 4^4) =-9800 (9\pi) (-225) = 70.8 \times10^6 \ J$$

مثال ۷

کابلی به طول ۴۰ متر و وزن ۵ کیلوگرم بر متر از سقف ساختمان بسیار بلندی آویزان شده است. مقدار کار موردنیاز برای بالا بردن تمام کابل به سقف چه‌ مقدار است؟

پاسخ: فرض کنید x متر از کابل بالا برده شده است، بنابراین $$40-x$$ متر از کابل با جرمی برابر $$5 \times (40-x)$$ آویزان است. وزن قسمت آویزان برابر است با:

$$= 9.8 \times 5(40-x) = 49 (40 - x) \ N$$

مقدار کار لازم برای بالا بردن کابل به مسافت $$\triangle x$$ برابر است با:

$$W= 49 (40 - x) \triangle x \ N$$

با جمع بستن کار کل انجام شده در فاصله صفر تا ۴۰ متر داریم:

$$W= \sum_{i =1} ^n 49 (40 - x) \triangle x \rightarrow \int_{0}^{40 } 49 (40 - x) dx$$

انتگرال فوق را در بازه داده شده محاسبه می‌کنیم:

$$W = \int_{0}^{40 } 49 (40 - x) dx \ J = 49 (40 x - \frac{x^2}{2})|_0^{40} \ J = 49 (40 (40) - \frac{(40)^2}{2}) \ J = 49 (800) \ J = 39200 \ J$$

مثال ۸

نیروی متغیر $$F_x$$ (نشان داده شده در شکل زیر) به ذره‌ای وارد می‌شود. مقدار کار انجام شده توسط نیروی وارد شده بر ذره را در:

1. فاصله مکانی صفر تا ۵/۰ متر
2. فاصله مکانی ۵/۰ تا ۱۰ متر
3. فاصله مکانی ۱۰ تا ۱۵ متر، به‌دست آورید.
4. مقدار کار کل انجام شده در فاصله مکانی صفر تا ۱۵ متر چه مقدار است؟

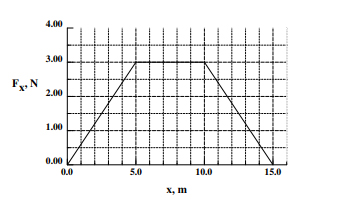
پاسخ: در این‌جا، نیروی وارد شده بر جسم بر حسب مکان تغییر می‌کند. بنابراین، از رابطه ساده $$W=F_x x$$ نمی‌توانیم استفاده کنیم. برای محاسبه کار، از تعریف کلی‌تر کار استفاده می‌کنیم:

$$W = \int_{x_i}^{x_f }F_x dx$$

رابطه بالا برابر مساحت زیر نمودار $$F_x$$ بر حسب x است.

قسمت ۱: در این قسمت، مساحت زیر نمودار نیرو بر حسب فاصله را از x=۰ تا x=۵/۰ به‌دست می‌آوریم. همان گونه که در شکل مشاهده می‌شود، مساحت این قسمت برابر مساحت مثلث قائم‌الزاویه‌ای به ارتفاع ۳/۰ (نیوتن) و قاعده ۵/۰ متر است. بنابراین، کار انجام شده برابر است با:

 $$W = \frac{‌1}{2} (3.0 \ N) (5.0 \ m) = 7.5 \ J$$

قسمت ۲: مساحت زیر نمودار در فاصله مکانی ۵/۰ تا ۱۰/۰ متر برابر با مساحت مستطیل کاملی به عرض ۳/۰ (نیوتن) و طول ۵/۰ (متر) است. در نتیجه، مقدار کار انجام شده در این فاصله زمانی برابر است با:

$$W = (3.0 \ N) (5.0 \ m) = 15.0 \ J$$

قسمت ۳: برای حرکت ذره در فاصله مکانی ۱۰/۰ تا ۱۵/۰ متر، مساحت ناحیه زیر نمودار برابر مساحت مثلث قائم‌الزاویه‌ای به ارتفاع ۳/۰ (نیوتن) و قاعده ۵/۰ (متر) است. بنابراین، مقدار کار انجام شده برابر است با:

$$W = \frac{‌1}{2} (3.0 \ N) (5.0 \ m) = 7.5 \ J$$

قسمت ۴: مقدار کار کل انجام شده در فاصله بین صفر تا ۱۵/۰ متر برابر با جمع جبری کارهای انجام شده در هر ناحیه است:

$$W_{total} = 7.5 \ J + 15.0 \ J + 7.5 \ J = 30.0 \ J$$

مثال ۹

مقدار کار انجام شده توسط نیروی $$\overrightarrow{F} = (2x \ N)\overrightarrow{i}+ (3 \ N) \overrightarrow{j}$$ (x بر حسب متر است) را برای جابجایی ذره‌ای از موقعیت $$r_i = (2 \ m) \overrightarrow{i} + (3 \ m) \overrightarrow{j}$$ به $$r_f = -\ (4 \ m) \overrightarrow{i} -\ (3 \ m) \overrightarrow{j}$$ به‌دست آورید.

پاسخ: در حالت کلی، رابطه کار در دوبعد به صورت زیر نوشته می‌شود:

$$W= \int_{x_i}^{x_f} F_x(\overrightarrow{r}) dx + \int_{y_i}^{y_f}F_y(\overrightarrow{r})dy$$

$$F_x = 2x$$ و $$F_y = 3$$، بنابراین داریم:

$$W= \int_{2 \ m}^{-4 \ m} 2x dx + \int_{3 \ m }^{-3 \ m}3dy \\ = x^2 |_{2 \ m} ^ { -\ 4 \ m} + 3y \ |_{3 \ m} ^ { -\ 3 \ m} = [(16-(4)] \ J + [(-9) - (9)] \ J = -\ 6 \ J$$

اکنون می‌توانیم به خوبی به پرسش کار چیست پاسخ دهیم. پس از آشنایی با کار انجام شده توسط نیروهای پایستار، غیرپایستار و نیروهای متغیر، در مورد کار انجام شده توسط نیروهای جاذبه و فنر صحبت خواهیم کرد.

کار نیروی جاذبه

برای پاسخ به پرسش کار چیست و درک بهتر ان، در مورد کار انجام شده در مورد نیروهای ثابت و متغیر و روش محاسبه آن ها صحبت کردیم. برای درک بهتر مفهوم کار چیست نیاز به محاسبه کار انجام شده توسط دو نیروی بسیار پرکاربرد در زندگی روزمره است. در ابتدا، در مورد کار انجام شده توسط نیروی جاذبه صحبن می‌کنیم.

نیروی جاذبه نیرویی است که سبب سقوط اجسام می‌شود. به بیان دیگر، نیروها توانایی انجام کار دارند (تغییر انرژی سیستم و تبدیل آن به دیگر شکل‌های انرژی). آیا این بدان معنا است که گرانش کار انجام می‌دهد؟

بله، گرانش کار انجام می دهد، زیرا انرژی پتانسیل را به انرژی جنبشی تبدیل می‌کند. توجه به این نکته مهم است که گرانش تنها در جهت نیروی جاذبه کار انجام می‌دهد.

این نکته که گرانش تنها در راستای نیرو کار انجام می دهد، به ویژگی نیروی پایستار، یعنی استقلال از مسیر حرکت، مربوط می شود. بنابراین، کار نیروی انجام شده توسط گرانش، تنها به کل جابجایی در جهت نیروی جاذبه، وابسته است. فرض کنید پرتقالی به پایین (به طرف زمین) سقوط می‌کند. نیروی جاذبه برابر حاصل‌ضرب جرم پرتقال در شتاب جاذبه است. کار انجام شده توسط گرانش (نیروی جاذبه زمین) برابر با W=mgh خواهد بود (h ارتفاعی است که پرتقال از آن سقوط کرده است). در این حالت، فرض کنید که پرتقال مسیر ساده‌ خط مستقیم را طی کرده است.

اکنون، فرض کنید پرتقال مسیر پیچیده‌ای را طی می‌کند. آیا کار انجام شده توسط نیروی گرانش بزرگ‌تر است؟ خیر. کار انجام شده توسط نیروی گرانش مستقل از مسیر حرکت است و تنها به نقطه‌های ابتدایی و انتهایی مسیر بستگی دارد.

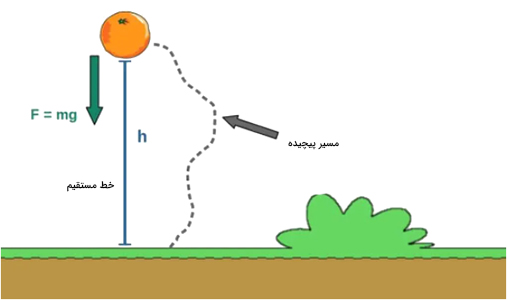
انرژی پتانسیل جاذبه به کار انجام شده توسط گرانش مربوط می‌شود و با آن رابطه تنگاتنگی دارد. به رابطه کار انجام شده توسط نیروی جاذبه دقت کنید (W=mgh). این رابطه با رابطه مربوط به انرژی پتانسیل جاذبه یعنی U=mgh، یکسان است.

انرژی پتانسیل جاذبه به صورت مقدار کار موردنیاز برای حرکت جسمی در خلاف جهت نیروی جاذبه، تعریف می‌شود. 

با توجه به آن‌که انرژی پتانسیل به صورت کار انجام شده در مقابل جاذبه تعریف شده است، علامت کار انجام شده و انرژی پتانسیل همواره مخالف یکدیگر خواهند بود. این مورد برای تمام نیروهای پایستار صدق می‌کند.

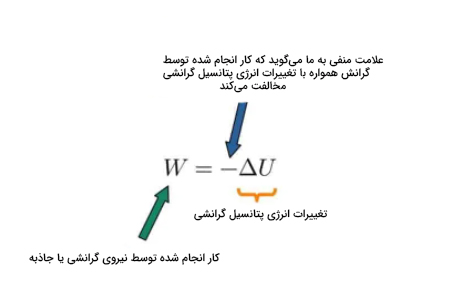
به این مثال توجه کنید. جسمی به علت جاذبه زمین به سمت پایین سقوط می‌کند. از آنجایی که ارتفاع آن کاهش می‌یابد، تغییرات انرژی پتانسیل منفی خواهد بود. همچنین، از آنجایی که $$\triangle U$$ منفی است، کار انجام شده مثبت خواهد بود (علامت مخالف). کار مثبت به معنای افزایش انرژی جنبشی است (قضیه کار و انرژی).

به بیان دیگر، اگر کار انجام شده توسط نیروی گرانش منفی بود، انرژی جنبشی کاهش و انرژی پتانسیل کاهش می‌یافت. به عنوان مثال، هنگامی که توپی را به سمت بالا پرتاب می‌کنیم، سرعت آن کاهش و ارتفاع آن از سطح زمین زیاد می‌شود، بنابراین انرژی جنبشی کاهش و انرژی پتانسیل افزایش می‌یابند.

کار انجام شده توسط گرانش می‌تواند بر حسب تغییرات انرژی جنبشی نیز بیان شود. به این نکته توجه داشته باشید که برای این حالت، علامت مقدار کار انجام شده و تغییرات انرژی جنبشی یکسان هستند.

$$W = \triangle K$$

نتیجه می‌گیریم که تغییرات انرژی جنبشی برابر تغییرات انرژی پتانسیل خواهد بود، اما علامت آن‌ها مخالف یکدیگر است. افزایش مقدار انرژی جنبشی برابر کاهش مقدار انرژی پتانسیل خواهد بود.

$$\triangle K = -\triangle U$$

نکته‌های مهم این قسمت عبارت هستند از:

• هر زمانی که جسمی در راستای نیروی جاذبه حرکت کند، گرانش کار انجام خواهد داد.
• کار انجام شده توسط جاذبه تنها به جابجایی کل در راستای نیروی جاذبه بستگی دارد.
• کار انجام شده توسط جاذبه معادل انرژی پتانسیل تبدیل شده به انرژی جنبشی و برعکس، است.

محاسبه کار انجام شده توسط جاذبه

به تنها فرمولی که برای محاسبه کار انجام شده توسط جاذبه نیاز داریم، تعریف کار است که در ابتدای مطلب عنوان شد.

$$W = F\triangle r cos \theta$$

در این رابطه، ‌F نیروی جاذبه، $$\triangle r$$ مقدار جابجایی کل و $$\theta$$ زاویه بین نیرو و جابجایی هستند. اگر جسمی بر روی زمین حرکت کند، مقدار کار انجام شده توسط نیروی جاذبه برابر صفر است. زیرا نیروی جاذبه بر جابجایی عمود است.

پس از درک بهتر پرسش کار چیست و محاسبه کار انجام شده توسط نیروی وزن، به حل مثال‌های زیر توجه کنید.

مثال اول کار انجام شده توسط نیروی جاذبه

می‌دانیم که جاذبه سبب افتادن جسم می‌شود. بنابراین، انرژی پتانسیل آن تغییر خواهد کرد. بنابراین، آیا جاذبه بر روی جسم در حال سقوط، کار انجام می‌دهد؟

جاذبه بر روی هر جسم در حال سقوطی، کار انجام می‌دهد. مقدار این کار تنها به تغییر ارتفاع بستگی دارد:

$$W=mg\triangle h$$

اگر ارتفاع جسمی تغییر نکند، جاذبه کار انجام نخواهد داد.

توپ بسکتبالی را در ارتفاع h از سطح زمین نگه داشته‌ایم.

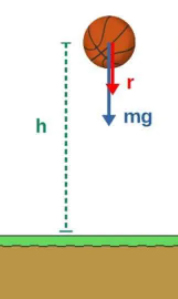
$$\trriangle r$$

کار انجام شده توسط نیروی جاذبه بر روی سطح شیبدار

فرض کنید جسمی بر روی سطح شیبداری قرار گرفته است. جسم به‌ دلیل نیروی جاذبه شروع به پایین آمدن از سطح شیبدار می‌کند. آیا جاذبه کار انجام می‌دهد؟

بله، جاذبه در این حالت نیز بر روی جسم کار انجام می‌دهد. مقدار کار تنها به تغییر ارتفاع بستگی دارد. به بیان دیگر، کار انجام شده توسط جاذبه بر روی سطح شیبدار با استفاده از رابطه W=mgh به‌دست می‌آید. این رابطه مشابه رابطه به‌دست آمده برای جسمی است که آزادانه سقوط می‌کند. چرا؟ آیا مقدار کار انجام شده به زاویه سطح شیبدار بستگی دارد؟ خیر. به تصویر زیر دقت کنید.

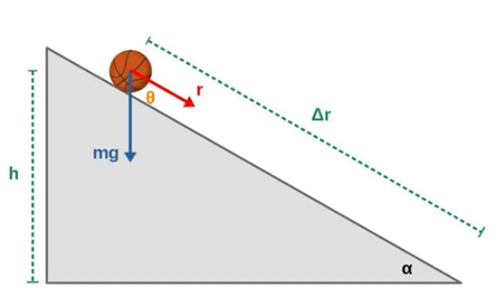
جسم در ارتفاع h از سطح زمین قرار گرفته است. نیروی جاذبه در جهت پایین به جسم وارد می‌شود. جابجایی آن بر روی سطح شیبدار برابر $$\triangle r$$ است. مقدار کار انجام شده توسط نیروی اصطکاک برابر است با:

$$W = \overrightarrow{F} . \overrightarrow{r} = mg\ (\triangle r) (cos \theta)$$

$$\theta$$ زاویه بین نیروی جاذبه (نیروی وزن) و جابجایی است. اکنون مثلت قرمز نشان داده شده در تصویر را در نظر بگیرید:

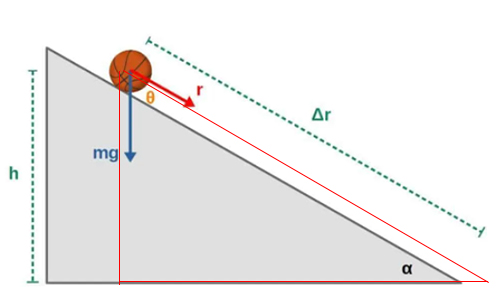
$$cos \theta$$ را با توجه به مثلث نشان داده شده می‌نویسیم:

$$cos \theta = \frac{h}{\triangle r} \Rightarrow h cos \theta = \triangle r$$

نکته جالب در مورد این مثال آن است که کار انجام شده توسط جاذبه به شیبدار بودن سطح بستگی ندارد، بلکه تنها به جابجایی کل انجام شده وابسته است: تغییرات ارتفاع.

کار انجام شده توسط جاذبه بر روی آونگ

آونگ سیستمی است که در آن جرمی تحت جاذبه زمین، نوسان می‌کند. آیا جاذبه در این حالت کاری انجام می دهد؟

بله، جاذبه بر روی آونگ کار انجام می دهد، زیرا ارتفاع آونگ پیوسته تغییر می‌کند. مقدار کاری که جاذبه بر روی آونگ انجام می دهد تنها به تغییر ارتفاع آن از سطح زمین بستگی دارد و برابر W=mgh است. به تصویر زیر توجه کنید. آونگ از ارتفاع h بالاتر از سطح زمین رها می‌شود.

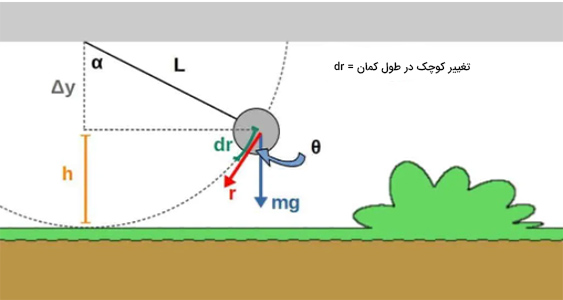
نخستین موردی که به آن توجه خواهیم کرد، رابطه بین زاویه‌های $$\alpha$$ و $$\theta$$ است.

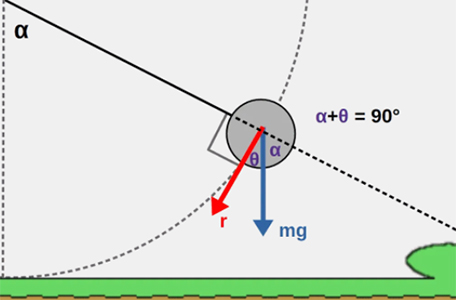
با توجه به تصویر نشان داده شده داریم:

$$\theta + \alpha = 90^o \ \Rightarrow \theta = 90^o - \alpha$$

همچنین، می‌توانیم جابجایی جسم را به راحتی به‌دست آوریم. این جابجایی برابر طول کمان نشان داده شده در تصویر زیر است.

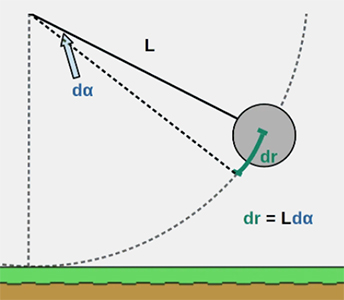
سیستم آونگ نسبت به سیستم‌های بیان شده در دو مثال قبل، پیچیده‌تر است. آسان‌ترین راه برای محاسبه کار انجام شده توسط جاذبه، استفاده از تعریف کار است:

$$W = \int_{r_1}^{r_2} \overrightarrow{F} . d \overrightarrow{r}= \int_{r_1}^{r_2} Fdr \ cos\theta$$

dr برابر طول کمان نشان داده شده در تصویر فوق است. همچنین، با استفاده از رابطه بین $$\theta$$ و $$\alpha$$، رابطه دیگری برای $$cos\theta$$ به‌دست می‌آوریم:

$$cos\theta = cos (90^o - \alpha) \ \parallel \ \theta = 90^o - \alpha$$

با جایگذاری رابطه‌های فوق، مقدار کار را به‌دست می‌آوریم:

$$W = \int_{r_1}^{r_2} Fdr\ cos\theta = mgL \int_{\alpha}^{0} sin\alpha \ d\alpha$$

محاسبه انتگرال فوق بسیار راحت است:

$$W = mgL \int_{\alpha}^{0} sin\alpha \ d\alpha = mgL (cos \alpha - 1)$$

رابطه به‌دست آمده برای کار را کمی ساده‌تر می‌کنیم. به تصویر زیر دقت کنید.

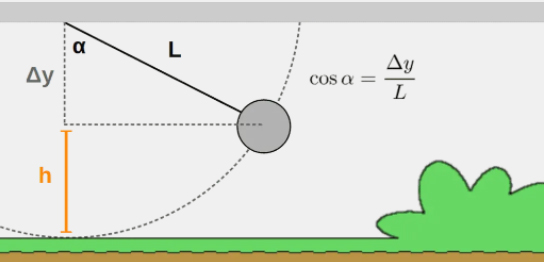
با توجه به تعریف کسینوس داریم:

$$cos \alpha = \frac{\triangle y}{L}$$

رابطه فوق را در رابطه به‌دست آمده برای کار قرار می‌دهیم:

$$W = mgL (cos \alpha - 1) = mgL(\frac{\triangle y}{L}-1) = mg (\triangle y - L)$$

اما معنای $$\triangle y - L$$ چیست؟ هنگامی که آونگ در حالت عمودی قرار دارد، این رابطه $$\triangle y + h = L$$ برقرار است. بنابراین، داریم:

$$\triangle y -L = -h \\ W = mg (\triangle y - L) = -mgh$$

اگر جهت رو به پایین را جهت مثبت در نظر بگیریم، رابطه کار به صورت زیر نوشته خواهد شد:

$$W = mgh$$

شاید مثال آونگ کمی پیچیده به‌ نظر برسد، اما کار انجام شده توسط جاذبه mgh است. اما سوالی که مطرح می‌شود آن است که کار انجام شده توسط نیروی جاذبه، کجا می‌رود؟ این کار تبدیل به انرژی جنبشی می‌شود. به عنوان مثال، سرعت آونگ افزایش خواهد یافت. مقدار انرژی جنبشی به‌دست آمده توسط آونگ برابر با کار انجام شده توسط نیروی جاذبه است (اصل پایستگی انرژی).

هنگامی که آونگ در پایین‌ترین نقطه قرار دارد، تمام انرژی پتانسیل به انرژی جنبشی تبدیل شده است. در واقع، در این نقطه، کار انجام شده توسط جاذبه برابر انرژی جنبشی آونگ است. در این حالت فرض شده است که آونگ از ارتفاع h و از حالت سکون رها شده است، بنابراین انرژی جنبشی و سرعت اولیه آن برابر صفر خواهد بود.

$$W = \frac{1}{2}m v^2$$

همان گونه که محاسبه شد، کار انجام شده برابر mgh است:

$$\frac{1}{2}m v^2 = mgh$$

با استفاده از رابطه فوق، سرعت حرکت آونگ را به‌‌دست می‌آوریم:

$$v = \sqrt{2gh}$$

می‌دانیم که آونگ به صورت رفت و برگشتی نوسان می‌کند. بنابراین، هنگامی که آونگ به بیشینه ارتفاع می‌رسد، انرژی جنبشی به انرژی پتانسیل تبدیل می‌شود. در اینجا از مقاومت هوا که به عنوان نیروی مخالف حرکت عمل می‌کند، چشم‌پوشی شده است، در نتیجه ارتفاع بیشینه با ارتفاعی که آونگ از آن رها شده است، یکسان خواهد بود. در حالت ایده‌آل، تغییرات انرژی پتانسیل به جنبشی و برعکس، پیوسته رخ می‌دهند.

کار انجام شده بر روی ماهواره ای که به دور زمین می چرخد

هنگامی که ماهواره‌ای به فضا پرتاب می‌شود، در مداری به دور زمین قرار داده می‌شوند. در این مدار، نیروی جاذبه زمین بر ماهواره وارد می‌شود و آن را در مدار نگه می‌دارد. بنابراین، آیا جاذبه بر روی ماهواره‌ای که به دور زمین می‌چرخد کار انجام می‌دهد؟

جاذبه بر روی ماهواره‌ چرخان به دور زمین، کار انجام نمی‌دهد. مدار ماهواره به طور تقریب دایره‌ای است و جابجایی آن بر نیروی جاذبه عمود است. بنابراین، کار انجام شده توسط نیروی جاذبه بر روی ماهواره برابر صفر خواهد بود. اگر مدار چرخش بیضی باشد، آیا نیروی جاذبه کار انجام می‌دهد؟ بله، در این حالت نیروی جاذبه حول کمانی کوچک، کار انجام خواهد داد. اما به این نکته توجه داشته باشید که کار کل انجام شده در چرخش کامل برابر صفر است.

در ابتدا، مدار دایره‌ای را در نظر می‌گیریم (مدار دایره‌ای حالت ایده‌آل است، در حالت واقعی مدارها کم‌و‌بیش به‌شکل بیضی هستند). در مدار دایره‌ای، نیروی جاذبه همواره به طرف مرکز زمین قرار دارد و جابجایی بر مدار حرکت مماس است. بنابراین، زاویه بین بردارهای نیرو و جابجایی برابر ۹۰ درجه است و کار انجام شده توسط جاذبه بر روی ماهواره، صفر خواهد بود.

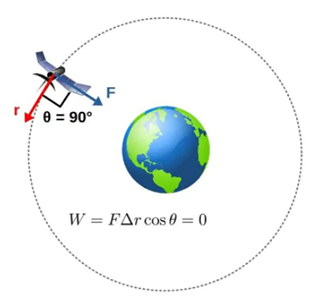
به این نکته توجه داشته باشید که جهت بردار r (جابجایی) در جهت حرکت و نه در راستای شعاع دایره، قرار دارد.

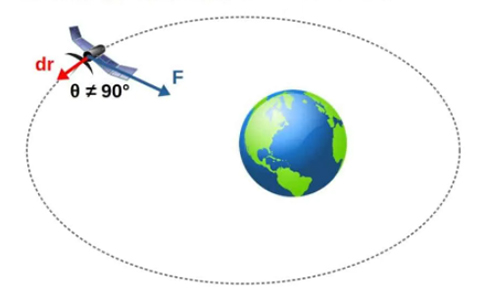
اکنون به دنیای واقعی بازمی‌گردیم. مدارهای واقعی به‌دلیل عامل‌های زیادی، دایره کامل نیستند و بیضی‌شکل هستند. در مدار بیضی، جهت حرکت همواره بر نیروی جاذبه عمود نیست. بنابراین، کار انجام شده توسط نیروی جاذبه صفر نخواهد بود. در واقع، کار انجام شده توسط جاذبه در قسمت‌های کوچکی از مدار (کار لحظه‌ای) صفر نیست.

کار کل انجام شده در مدار کامل، صفر باقی می‌ماند. این جمله به پایستگی تکانه زاویه‌ای در مدارهای ثابت (دایره‌ای یا بیضی) مربوط است.

کار لحظه‌ای $$dW = Fdr\ cos\theta\neq 0$$

کار کل انجام شده در مدار $$W = \oint\overrightarrow{F}.d \overrightarrow{r}= 0$$

تاکنون به پرسش کار چیست برای نیروهای مختلف، ثابت و متغیر، پاسخ دادیم. در ادامه، کار نیروی انجام شده توسط فنر را محاسبه می‌کنیم.

کار نیروی فنر

فنر می‌تواند به جسم متصل به آن نیرو وارد کند. نیروی فنر شباهت بسیار زیادی به نیروی جاذبه دارد. اما تفاوت بسیار مهم آن با نیروی جاذبه آن است که اندازه نیروی فنر با جابجایی تغییر می‌کند.

نیروی فنر

نیروی فنر با استفاده از رابطه زیر داده می‌شود:

$$F= -kx$$

در رابطه فوق، k ثابت فنر، x مقدار کشیدگی آن و F نیروی وارد شده است. مقدار k را می‌توان به طور تجربی برای هر فنری به‌دست آورد. ثابت فنر مقدار سختی فنر را نشان می‌دهد. هرچه مقدار آن بزرگ‌تر باشد، برای تغییر طول فنر باید نیروی بیشتری وارد شود. به رابطه بین نیرو و جابجایی در فنر، قانون هوک نیز گفته می‌شود. این قانون هنگامی برقرار است که:

• جرم فنر قابل چشم‌پوشی باشد.
• هیچ نیروی اتلافی (مانند اصطکاک) وجود نداشته باشد.

مقدار x را چگونه اندازه می‌گیریم؟ x برابر مقدار کشیدگی فنر نسبت به طول طبیعی است. طول طبیعی فنر طولی است که فنر کشیده یا فشرده نشده است. این حالت را مبدا مختصات در نظر می‌گیریم.

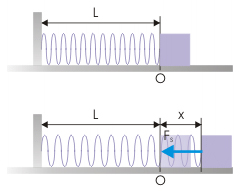
علامت منفی در رابطه فوق بسیار مهم است. این علامت نشان‌دهنده آن است که نیروی فنر همواره مخالف جهت جابجایی است. در واقع، جهت نیروی فنر همواره به طرف مبدا یا موقعیت تعادلی فنر (طول طبیعی) خواهد بود. به تصویر زیر توجه کنید. همان‌ گونه که در تصویر نشان داده شده است، جهت نیروی فنر همواره به سمت مرکز است و در تلاش برای برگردان فنر به طول طبیعی است.

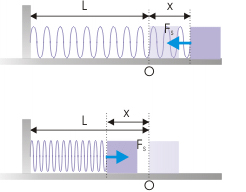
کار فنر

کشیدگی در فنر ایده‌آل به‌ طور مستقیم متناسب با نیروی فنر است:

$$F = -kx$$

 انرژی پتانسیل ذخیره شده در فنر برابر $$U = -\ \frac{1}{2}kx^2$$ است.

اکنون، رابطه مربوط به انرژی پتانسیل را به‌دست می‌آوریم. فرض کنید فنر را به اندازه dx از حالت تعادل می‌کشیم. مقدار کار انجام شده به هنگام کشیدگی فنر برابر است با:

$$dW = F\ dx$$

F مقدار نیرویی است که برای کشیدن فنر به آن وارد می‌شود. کار کل انجام شده برای کشیدن فنر از مقدار تعادل، یعنی x=0، تا مقدار x متر با استفاده از انتگرال زیر به‌دست می‌آید:

$$\int dW = \int_{0}^{x} F \ dx$$

با جایگذاری F = -kx داریم:

$$W = \int_{0}^{x}-kxdx = -k \int_{0}^{x} x\ dx = -k[\frac{x^2}{2}]_0^x = -\ \frac{1}{2}kx^2$$

این کار انجام شده توسط فنر چیزی جز انرژی پتانسیل فنر نیست:

$$U = -\ \frac{1}{2}kx^2$$

اگر تنها نیروی وارد بر جسم نیروی فنر باشد، مقدار کار از رابطه فوق به‌دست خواهد آمد. در حرکت به سمت راست، نیروی فنر در خلاف جهت حرکت بر جسم وارد خواهد شد. مقدار آن با افزایش جابجایی، افزایش می‌یابد. بنابراین، فنر با انجام کار منفی بر روی جسم، انرژی را از آن منتقل می‌کند. در نتیجه، انرژی جنبشی جسم (سرعت آن) کاهش خواهد یافت.

این روند تا هنگامی ادامه می یابد که انرژی جنبشی و سرعت جسم صفر شوند. سپس، فنر جسم را به سمت مبدا و در جهت منفی محور x می‌کشاند. در این حالت، نیروی فنر در جهت حرکت است. بنابراین، با انجام کار مثبت بر روی جسم، انرژی را به آن منتقل می‌کند.

این روند تا بازگشت ذره به مکان اولیه ادامه می‌یابد. در این هنگام، سرعت آن برابر سرعت اولیه است. از انجایی که هیچ نیروی اتلافی مانند نیروی اصطکاک وجود ندارد، انرژی جنبشی جسم در بازگشت برابر انرژی جنبشی آن در شروع حرکت است.

$$K_f= K_i$$

در حرکت رفت و برگشتی، مقدار کار کل برابر صفر خواهد بود. همچنین، انرژی کل منتقل شده به جسم یا انتقال یافته از آن، برابر صفر است. مقدار انرژی جنبشی اولیه با مقدار انرژی جنبشی در انتهای مسیر برابر خواهد بود. بنابراین، با کمی دقت متوجه خواهیم شد که حرکت تحت نیروی فنر شباهت زیادی به حرکت تحت نیروی جاذبه دارد.

جسم با انرژی جنبشی برابر انرژی جنبشی اولیه به نقطه شروع بازگشته است، پس از آن چه اتفاقی رخ خواهد داد؟ جسم دارای سرعتی به سمت چپ است. بنابراین، پس از عبور از مبدا، به سمت چپ حرکت می‌کند. اما نقش نیرو فنر را نباید فراموش کنیم. با حرکت جسم به سمت چپ، فنر فشرده می‌شود. نیروی فنر سعی در برگرداندن جسم به حالت تعادل (مبدا) دارد. بنابراین، در خلاف جهت حرکت اعمال خواهد شد.

با افزایش فشردگی فنر، مقدار نیروی آن افزایش و انرزی جنبشی جسم کاهش می‌یابد. هنگامی که فنر به بیشینه فشردگی خود می‌رسد، مقدار انرژی جنبشی صفر و مقدار انرژی پتانسیل ذخیره شده در فنر، بیشینه خواهد بود. پس از آن، نیروی فنر جسم را به نقطه تعادل بازمی‌گرداند. اگر از نیروی اتلافی چشم‌پوشی شود، این روند ادامه می‌یابد و جسم حول مبدا نوسان می‌کند.

مثال اول کار نیروی فنر

جسمی به جرم ۲ کیلوگرم به فنر افقی متصل شده است. اگر ثابت فنر برابر ۵۰۰ نیوتن بر متر باشد و به اندازه ۱۰ سانتی‌متر کشیده شده باشد، کار انجام شده توسط نیروی افقی خارجی را به‌دست آورید. فرض کنید نیروی فنر به‌‌آهستگی آن را می‌کشد.

پاسخ: به عبارت «به آهستگی» دقت کنید. از این عبارت می‌توان به این نتیجه رسید که جسم بدون انرژی جنبشی کشیده می‌شود. در این حالت، سرعت‌های اولیه و نهایی و در نتیجه انرژی جنبشی معادل، برابر صفر هستند. بنابراین، طبق قضیه کار و انرژی، کار انجام شده توسط دو نیروی خارجی اعمال شده و فنر برابر صفر است. در نتیجه، کار انجام شده توسط نیروی افقی (نیروی خارجی اعمال شده) برابر کار انجام شده توسط نیروی فنر است (با علامت مخالف). کار انجام شده توسط نیروی فنر برابر است با:

$$W_S = -\ \frac{1}{2}kx^2 = -\ \frac{1}{2}\times (500) \times (0.1)^2 \\ W_S = -\ 2.5 \ J$$

کار انجام شده توسط نیروی افقی برابر است با:

$$W = -\ W_S = -\ (- \ 2.5 \ J) = 2.5 \ J$$

باید به این نکته توجه کنیم که این مثال به طور دقیق شبیه جاذبه است. به منظور به‌دست آوردن هر نیروی خارجی، کار انجام شده توسط نیروی فنر را محاسبه می‌کنیم.

توجه به این نکته مهم است که کار انجام شده توسط فنر برای هر جابجایی دلخواهی، مستقل از حضور نیروهای دیگر است. کار انجام شده توسط نیروی فنر یکسان باقی خواهد ماند. طبق قضیه کار و انرژی داریم:

$$K_f - K_i = W_S + W_F$$

در رابطه فوق، $$W_S$$ و $$W_F$$ به‌ ترتیب کار انجام شده توسط فنر و نیروهای اعمال شده هستند.

تحلیل کار انجام شده توسط نیروهای خارجی با توجه به نکته‌های زیر انجام می‌شود:

1. سرعت‌های اولیه و نهایی برابر صفر هستند.
2. سرعت‌های اولیه و نهایی یکسان هستند.
3. سرعت‌های اولیه و نهایی متفاوت هستند.

در دو حالت اول، سرعت‌های اولیه و نهایی یکسان هستند، در نتیجه انرژی جنبشی اولیه و نهایی نیز با یکدیگر برابر خواهند بود:

$$K_f - K_i = W_S + W_F \\ W_F = -W_S$$

این نتیجه بسیار مهم است. به راحتی می‌توانیم کار انجام شده توسط نیروی فنر را محاسبه کنیم و با قرار دادن علامت منفی، کار انجام شده توسط نیروهای دیگر را به‌دست آوریم.

در حالت سوم (سرعت‌های متفاوت)، انرژی جنبشی اولیه با نهایی برابر نیست. اما کار انجام شده توسط نیروی فنر بدون تغییر باقی می‌ماند. در نتیجه، تفییرات انرژی جنبشی برابر کار کل انجام شده توسط فنر و نیروهای دیگر است.

مثال دوم کار نیروی فنر

جسمی به جرم یک کیلوگرم با سرعت یک متر بر ثانیه به فنر افقی برخورد می‌کند. اگر ثابت فنر برابر ۱۰۰۰ نیوتن بر متر باشد، مقدار فشردگی آن را به‌دست آورید.

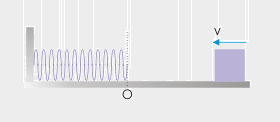
پاسخ: هنگامی که جسم به فنر برخورد می‌کند، آن را تا توقف کامل فشرده می‌کند. در این حالت، مقدار انرژی جنبشی اولیه و نهایی با یکدیگر برابر نیستند. زیرا جسم با سرعت مشخصی به فنر برخورد می‌‌کند، اما پس از بیشینه فشردگی فنر، سرعت آن برابر صفر خواهد بود. به این نکته توجه داشته باشید که تنها نیروی وارد شده بر جسم، نیروی فنر است.

$$K_f - K_i = W_S \\ \Rightarrow W_S = K_f - K_i = 0 - \frac{1}{2}mv^2 \\ \Rightarrow W_S = -\ 0.5 \times 1\times 1^2 = - \ 0.5 \ J$$

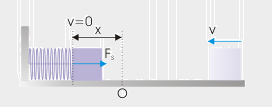
با استفاده از رابطه به دست آمده برای کار نیروی فنر، مقدار آن را محاسبه می‌کنیم:

$$‌W_S = -\ \frac{1}{2}kx^2 \\ \Rightarrow \ W_S = -\ 0.5 \times 1000\times x^2 = -500 \ x^2$$

با برابر قرار دادن رابطه‌های بالا، داریم:

$$-500 \ x^2 = - \ 0.5 \\ \Rightarrow x^2 = \frac{0.5}{500 } = 0.001\\ \Rightarrow x = 0.032 \ m$$

با توجه به اهمیت پرسش کار چیست، نمونه سوالات بیشتری در مورد کار نیروی ناپایستار و قضیه کار و انرژی حل می‌کنیم.

نمونه سوالات کار چیست

تا اینجا دیدیم که مفهوم کار چیست و با زبانی ساده با آن آشنا شدیم، در ادامه برای درک بهتر این مفهوم، پرسش‌های گوناگونی حل خواهند شد.

پرسش اول کار چیست

کدام‌یک از عبارت‌های زیر در مورد حرکت قطار اسباب‌بازی با سرعت ثابت بر روی حلقه، صحیح است؟

1. جاذبه تنها نیرویی است که بر روی قطار کار انجام می‌دهد.
2. دو نیرو بر قطار وارد می‌شوند، اما هیچ‌کدام از آن‌ها کاری بر روی قطار انجام نمی‌دهند.
3.  جمع تمام نیروهای وارد بر قطار برابر صفر است.
4. قطار شتاب می‌گیرد.

پاسخ: قطار با سرعت ثابتی بر روی ریل دایره‌ای حرکت می‌کند. در اینجا باید به حرکت دایره‌ای توجه کنیم. سرعت ثابت نشان‌دهنده سرعت مماسی است. در حلقه عمودی، دو نیرو بر جسم وارد می‌شوند:

• نیروی عمودی سطح
• نیروی جاذبه

اگر نیروی وارد شده بر جسم بر جابجایی آن عمود باشد، مقدار کار انجام شده برابر صفر خواهد بود. تنها در نقطه‌های بالا و پایین حلقه عمودی، جاذبه عمود بر جابجایی است.

اگر جمع تمام نیروهای وارد شده بر قطار برابر صفر باشد، قطار باید با سرعت ثابت بر خط راست حرکت کند یا بدون حرکت باشد. هنگامی‌ که جسمی حرکت دایره‌‌ای انجام می‌دهد، بزرگی سرعت یا تندی ثابت است، اما جهت آن پیوسته تغییر می‌کند. بنابراین، جسم به‌ دلیل تغییر جهت سرعت، با شتاب ثابت حرکت خواهد کرد.

با توجه به توضیحات فوق، پاسخ صحیح گزینه ۴ است.

نقش انرژی مصرفی جسمی به جرم m در کار چیست ؟

جسمی به جرم m از حالت سکون شروع به حرکت می‌کند و پس از گذشت مدت زمان t سرعت آن به v می‌رسد. کدام‌یک از گزینه‌های زیر انرژی مصرف شده در این بازه زمانی را نشان می‌دهد.

1. $$\frac{W}{t}$$
2. $$\frac{Fv}{t}$$
3. $$\frac{mv^2}{2t}$$
4. $$\frac{- \ mv^2}{t}$$

پاسخ: پاسخ صحیح گزینه ۳ است. توان به صورت نرخ انجام کار تعریف می‌شود. تعریف دیگر توان، انرژی مصرف شده در بازه زمانی مشخص، است. فرمول محاسبه به صورت زیر نوشته می‌شود:

$$P = \frac{\triangle W}{\triangle t} = \frac{\triangle E}{ t}$$

جسم متحرک همواره انرژی جنبشی به‌دست می‌آورد، بنابراین تغییرات انرژی جسمی که از حال سکون شروع به حرکت می‌کند، برابر است با:

$$P = \frac{\frac{1}{2}mv^2}{ t} = \frac{mv^2}{2 t}$$

نقش مسافت توقف در محاسبه کار چیست ؟

به مسافت طی شده از ترمز تا توقف کامل اتومبیل، مسافت توقف، d، گفته می‌شود. اتومبیل مسابقه‌ای به جرم m با سرعت ۱۰۰ متر بر ثانیه حرکت می‌کند. ضریب اصطکاک بین آسفالت خیس و لاستیک‌ها برابر ۰/۲۰ است، در حالی که ضریب اصطکاک بین آسفالت خشک و لاستیک‌ها می‌تواند به مقدار ۰/۹۰ برسد. با فرض آن‌که نیروی اصطکاک تمام کار لازم برای توقف اتومبیل را انجام می‌دهد، کدام‌یک از عبارت‌های نوشته شده در مورد مسافت توقف صحیح است.

1. مسافت توقف محاسبه شده بر روی آسفالت خیس ۴/۵ برابر بزرگ‌تر از توقف بر روی آسفالت خشک است.
2. مسافت توقف به طور مستقیم متناسب با سرعت اولیه اتومبیل است.
3. هرچه ضریب اصطکاک بزرگ‌تر باشد، مسافت توقف نیز بزرگ‌تر است.
4. هر دو اتومبیل از اصطکاک ایستایی برای توقف کامل استفاده می‌کنند.

پاسخ: قبل از پاسخ به این پرسش، معادله‌ای برای مسافت توقف به‌دست می‌آوریم. اتومبیل با سرعت اولیه $$v_0$$ حرکت می‌کند و پس از ترمز، به طور کامل متوقف می‌شود. بنابراین، انرژی جنبشی نهایی برابر صفر خواهد بود. با توجه به قضیه کار و انرژی، تغییرات انرژی جنبشی برابر کار انجام شده است. از آنجایی که اصطکاک تمام کار لازم برای توقف اتومبیل را انجام می‌دهد، کار انجام شده توسط نیروی اصطکاک عبارت است از:

$$\triangle K = W_{net} = - \ \mu mgd$$

با نوشتن رابطه مربوط به انرژی جنبشی، مسافت توقف را به‌دست می‌آوریم:

$$\triangle K = - \ \frac{1}{2}m v_0^2 = - \ \mu mgd \ \Rightarrow \ d = \frac{v_0^2}{2\mu g}$$

با توجه به رابطه به‌دست آمده برای مسافت توقف داریم:

• مسافت توقف به طور مستقیم با مجذور سرعت حرکت اولیه اتومبیل متناسب است.
• هر چه ضریب اصطکاک بزرگ‌تر باشد، مسافت توقف کوتاه‌تر خواهد بود.
• اگر اتومبیل مسابقه بر روی آسفالت خشک حرکت کند، برای توقف از اصطکاک ایستایی استفاده می‌کند.
• اگر اتومبیل مسابقه بر روی آسفالت خیس حرکت کند، برای توقف از اصطکاک جنبشی استفاده می‌کند.

با توجه به توضیحات فوق، پاسخ صحیح گزینه یک است.

نقش سطح شیبدار در محاسبه کار چیست ؟

جسمی به جرم ۱۰/۰ کیلوگرم بر روی تپه‌ای در ارتفاع ۳/۰ متری از سطح زمین قرار گرفته است. جسم از بالای تپه به پایین حرکت می‌کند و از میان زمین گل‌آلودی با ضریب اصطکاک ۰/۲۰ می‌گذرد. در ادامه، جسم از سطح شیبدار بدون اصطکاکی با زاویه ۴۵/۰ درجه بالا می‌رود. جسم تا چه ارتفاعی از سطح شیبدار بالا خواهد رفت؟

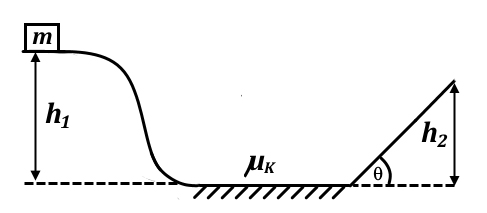
1. ۱/۰ متر
2. ۱/۵ متر
3. ۲/۰ کتر
4. ۲/۴ متر

پاسخ: در اینجا از صورت دیگر قضیه کار و انرژی برای نیروهای ناپایستار استفاده می‌کنیم.

$$W_{NC} = \triangle K + \triangle U = (\frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2) + (mgh_f - mgh_i)$$

از آنجایی که جسم از حالت سکون شروع به حرکت می‌کند و در پایان مسیر متوقف می‌شود، مقدار انرژی جنبشی اولیه و نهایی برابر صفر است با:

$$W_{NC} = mgh_f - mgh_i$$

با جایگذاری مقدار کار انجام شده توسط نیروی اصطکاک در رابطه فوق، داریم:

$$-\ \mu_kNd = - \ \mu_kmg d = mgh_f - mgh_i \ \Rightarrow \ -\ \mu_k d = h_2 - h_1 \\ h_2 = h_1 - \mu_kd$$

با قرار دادن مقدارهای داده شده در پرسش، جسم تا ارتفاع ۲/۴ متر از سطح شیبدار بالا خواهد رفت. بنابراین، پاسخ صحیح گزینه ۴ است.

جمع‌بندی

در این مطلب به پرسش کار چیست به زبان ساده پاسخ دادیم. در ابتدا، رابطه ریاضی کار را در فیزیک توضیح دادیم. در ادامه، در مورد رابطه میان کار و انرژی جنبشی و پتانسیل صحبت کردیم. در پایان، با روش محاسبه کار نیروهای متغیر، نیروی جاذبه و نیروی فنر آشنا شدیم.