نگاشت انقباضی (Contraction Mapping) — به زبان ساده

یکی از قضایای مهم در ریاضیات در شاخه توابع و «نگاشت‌ها» (Mappings) «قضیه نگاشت انقباضی» (Contraction Mapping Theorem) یا «قضیه نقطه ثابت باناخ» (Banach fixed-point Theorem) است که همگرایی و شرایط همگرایی توابع را مورد بحث قرار می‌دهد. در این قضیه براساس نظریه اندازه و فضای متریک، شرایط و خصوصیاتی مورد بحث قرار می‌گیرد که همگرایی را تضمین می‌کند. در این نوشتار به بررسی این قضیه و همچنین به یکی از کاربردهای آن در معادله کپلر اشاره خواهیم کرد. به عنوان پیش‌زمینه بهتر است مطلب محیط بیضی — به زبان ساده را بخوانید. همچنین مطالعه نوشتار قضیه مقدار میانگین (Mean Value Theorem) — به زبان ساده نیز خالی از لطف نیست.

بهتر است به عنوان مقدمه ابتدا قضیه نگاشت انقباضی را معرفی کرده و براساس آن محاسبات کپلر را مورد بررسی قرار دهیم. در انتها نیز به کمک یک کد پایتون، محاسبات مربوط به این قضیه را برای حل معادله کپلر بیان خواهیم کرد.

قضیه نگاشت انقباضی (Contraction Mapping Theorem)

برای آشنایی با این قضیه ابتدا باید با چند تعریف آشنا شویم. در گام اول فضای متریک را معرفی و سپس نگاشت انقباضی را بررسی می‌کنیم.

فیلم آموزش مبانی توپولوژی عمومی – جامع و کاربردی در فرادرس

کلیک کنید

متر و فضای متریک

یک مجموعه مثل $$X$$ به همراه «اندازه» (Measure) مثل $$d$$ که روی آن مجموعه تعریف می‌شود، فضای متریک نامیده می‌شود. معمولا فضای متریک را به صورت زوج مرتب $$(X,d)$$ نشان می‌دهند. در حقیقت اندازه، تابعی است که برای سنجش فاصله بین اعضای مجموعه $$X$$ به کار می‌رود. مشخص است که دامنه این تابع زوج‌هایی از مجموعه $$X$$ و برد آن نیز اعداد حقیقی هستند.

با فرض اینکه $$d: X\times X \to [0,\infty)$$ یک تابع فاصله باشد، به ازاء هر سه نقطه دلخواه x, y, z گزاره‌های زیر را می‌توان عنوان کرد:

1. $$d(x,y)\geq 0$$: این رابطه بیانگر نامنفی بودن تابع فاصله است.
2. $$d(x,y)=0 \longleftrightarrow x=y$$: این رابطه بیان می‌کند که اگر فاصله بین دو نقطه صفر باشد، دو نقطه یکی هستند. البته عکس این گزاره نیز صادق است. در حقیقت اگر دو نقطه یکسان باشند، فاصله بینشان صفر خواهد بود.
3. $$d(x,y)=d(y,x)$$: این رابطه، بیانگر خاصیت تقارنی برای تابع فاصله است.
4. $$d(x,z)\leq d(x,y)+d(y,z)$$: این رابطه به این معنی است که تابع فاصله در نامساوی مثلثی صدق می‌کند. یعنی فاصله دو نقطه x و z کمتر از مجموع فاصله x تا y و فاصله y تا z است. این موضوع به خوبی در فاصله اقلیدسی دیده می‌شود.

توابعی با خصوصیات گفته شده را گاهی «متریک» (Metric) نیز می‌نامند. برای مثال نقاط مربوط به مختصات دکارتی یعنی $$R^2$$ و فاصله اقلیدسی می‌توانند یک فضای متریک بسازند.

فضای کامل (Complete Space)

برای آنکه با «فضای کامل» (Complete Space) آشنا شویم لازم است ابتدا «دنباله کوشی» (Cauchy Sequence) را بشناسیم. فرض کنید $$\{x_n\}$$ یک دنباله باشد. اگر این دنباله در فضای متریک $$(X,d)$$ دارای خاصیت زیر باشد، به آن «دنباله کوشی» می‌گویند.

$$\large  \forall \epsilon >0 ,\; n,m >N;\;\; d(x_m,x_n)<\epsilon$$

به بیان دیگر می‌توان گفت که با افزایش جملات این دنباله، مقادیر آن به یکدیگر نزدیک و نزدیک‌تر می‌شوند، بطوری که می‌توان گفت این دنباله دارای حد است.

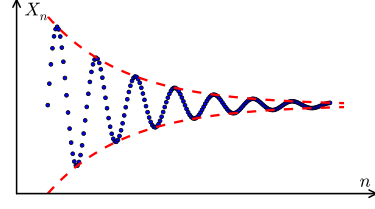
این نوع دنباله به افتخار دانشمند و ریاضی‌دان بزرگ فرانسوی «آگوستین کوشی» (Augustin-Louis Cauchy) که بخصوص در این زمینه تحقیقات زیادی کرده بود، «دنباله کوشی» نام‌گذاری شده است.

بنابراین اگر فضای متریک $$(X,d)$$ براساس دنباله کوشی ساخته شود، آن را یک «فضای متریک کامل» (Complete Metric Space) می‌نامند. به این ترتیب مشخص است که در فضای متریک کامل، هر دنباله‌ای، دارای حد بوده و به یک نقطه همگرا است.

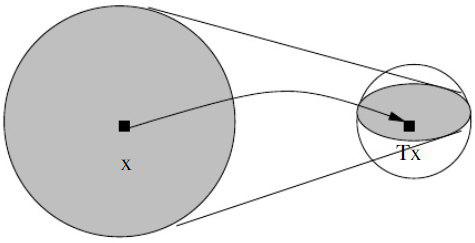
نگاشت انقباضی (Contraction Mapping)

فرض کنید فضای $$(X,d)$$ یک فضای متریک باشد. آنگاه نگاشت $$f$$ از $$X$$ به $$X$$ که به صورت $$f:X\rightarrow X$$ نشان داده می‌شود، یک نگاشت انقباضی است اگر مقداری مثل $$q\in [0,1)$$ وجود داشته باشد که شرط زیر برایش صادق باشد.

$$\large d(f(x),f(y))\leq qd(x,y) ,\;\;\;\forall x,y \;\;in \;X$$
رابطه ۱

این تعریف نشان می‌دهد که فاصله یا اندازه $$d$$ برای هر دو نقطه از نگاشت انقباضی همیشه از فاصله یا اندازه آن دو نقطه کمتر است. اگر بین نقطه $$x$$ و تابع $$f$$ رابطه $$f(x)=x$$ برقرار باشد، آنگاه $$x$$ را نقطه ثابت (Fixed point) تابع $$f$$ می‌نامند. حال به بررسی قضیه نگاشت انقباضی (Contraction Mapping) یا «قضیه نقطه ثابت باناخ» (Banach's Fixed Point Theorem) می‌پردازیم.

قضیه نگاشت انقباضی (Contraction Mapping Theorem)

فرض کنید $$(X,d)$$ یک فضای متریک کامل غیرتهی باشد. اگر $$f$$ یک نگاشت انقباضی به صورت $$f:X\rightarrow X$$ باشد، آنگاه برای چنین نگاشتی وجود یک نقطه $$x^*$$ به عنوان نقطه ثابت، تضمین می‌شود.

به بیان دیگر در یک فضای کامل با نگاشت $$f$$، نقطه‌ای مثل $$x^*$$ را می‌توان به عنوان نقطه ثابت پیدا کرد که برابر با حد دنباله $$\{x_n\}$$ باشد. برای این کار اولین جمله دنباله، یعنی $$x_0$$ را به طور اختیاری انتخاب کرده و بقیه جملات را به صورت زیر در نظر می‌گیریم.

$$\large x_n=f(x_{n-1})$$
رابطه ۲

با توجه به شرایط فضای کامل و نگاشت انقباضیِ $$f$$ خواهیم داشت:

$$\large x_n \rightarrow x^*$$
رابطه ۳

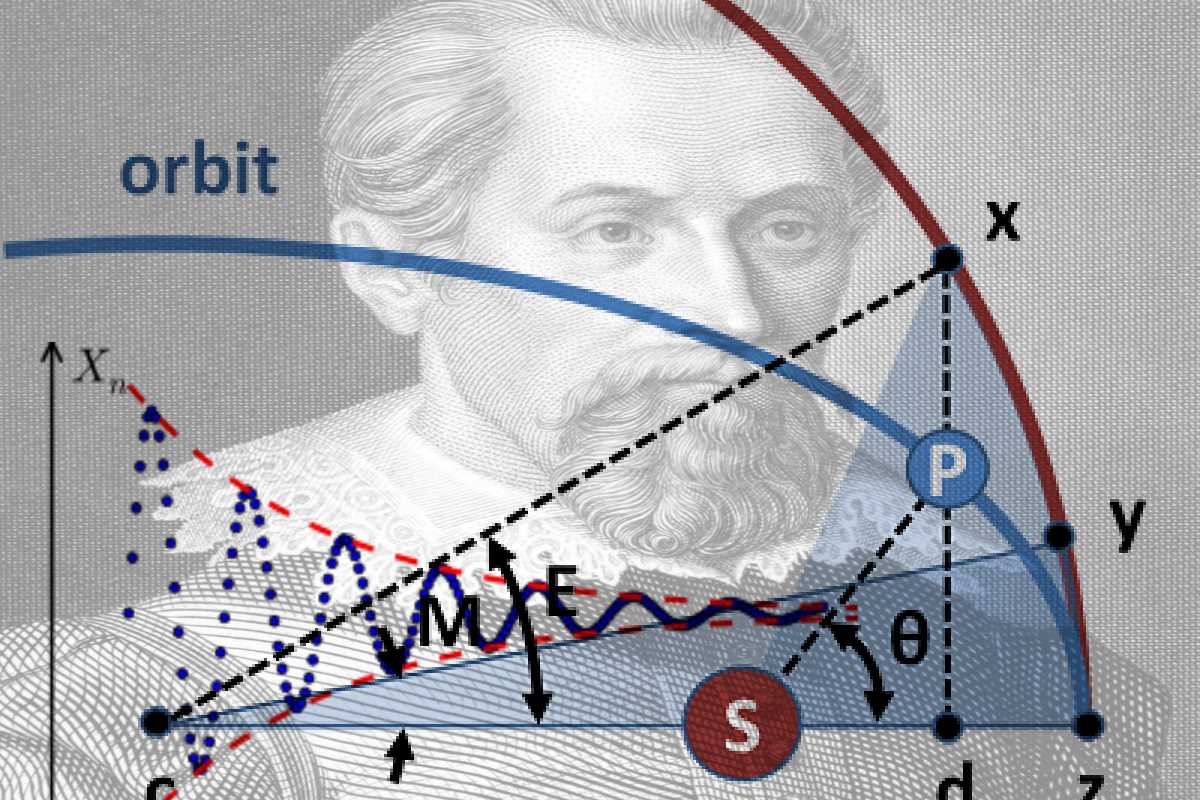
معادله کپلر (Kepler Equation) و کاربرد قضیه نگاشت انقباضی

کپلر به حرکت اجرام سماوی علاقمند بود. او سعی کرد وضعیت و حرکت سیارات و ستاره‌ها را پیش‌بینی کند. به این ترتیب با استفاده از اندازه‌گیری‌های دقیق و ریاضیات توانست نشان دهد که مدارات حرکت سیاره‌ها دور خورشید بیضوی بوده که خورشید در یکی از کانون‌های این بیضی قرار دارد.

در یک مدار بیضوی، «معادله کپلر» (Kepler Equation) به صورت زیر نوشته می‌شود.

$$\large M+e \sin E=E$$

در این رابطه، $$M$$ «آنومالی متوسط» (Mean Anomaly) و $$E$$ نیز «زاویه آنومالی» (Eccentric Anomaly) همچنین $$e$$ یا (Eccentricity) «خروج از مرکز» را نشان می‌دهد.

این پارامترهای ناهنجاری یا «آنومال» (Anomalies)، بیانگر موقعیت و حرکت اجرام سماوی بوده که در معادله کپلر، نشان‌دهنده مدارات کپلری هستند. کپلر بدون آنکه از قضیه نگاشت انقباضی و نقطه ثابت اطلاع داشته باشد، از آن استفاده کرده است.

کپلر متوجه شد که برای حل این معادله و پیدا کردن مقدار $$E$$، فرم بسته‌ای وجود ندارد. بنابراین او برای حل معادله به روشی تکراری دست زد. به این ترتیب او رابطه بالا را به صورت $$f(E)=E$$ نوشت که یک نگاشتِ نقطه ثابت است. به این ترتیب معادله بالا به صورت زیر نوشته خواهد شد.

$$\large f(E) =M+e \sin E$$

از آنجایی که مقدار آنومالی متوسط می‌تواند تقریب خوبی برای زاویه آنومالی باشد، کپلر از آن به عنوان نقطه آغازین اختیاری ($$x_0$$) استفاده کرد. البته دنباله‌ها یا تکرارها براساس هر نقطه آغازین، همگرا خواهند بود. البته صحت این عبارت را بعدا بررسی خواهیم کرد ولی با انتخاب نقطه آغازین مناسب، سرعت همگرایی بیشتر خواهد بود و زودتر به جواب خواهیم رسید.

اثبات همگرایی

هر چند کپلر قانون خود و محاسبه $$E$$ را در سال ۱۶۲۰ انجام داد ولی «استفان باناخ» (Stefan Banach) دانشمند و ریاضی‌دان لهستانی در قرن ۲۰ام «قضیه نقطه ثابت» را مطرح کرد. بنابراین به نظر می‌رسد که کپلر از صحت این قضیه آگاهی داشته ولی برای اثبات یا فرموله کردن آن تلاشی نکرده است.

فیلم آموزش جبر خطی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

در ریاضیات مدرن، خط اعداد حقیقی و فاصله قدرمطلق، یک فضای متریک کامل در نظر گرفته می‌شود. بنابراین کافی است نشان دهیم تابعی که به صورت $$f(E)$$ در بالا معرفی کردیم، یک نگاشت انقباضی است و یک نقطه ثابت دارد.

به این منظور از قضیه مقدار میانگین استفاده کرده، نشان می‌دهیم که قدر مطلق مشتق تابع $$f$$ کمتر از ۱ است. به این ترتیب می‌توانیم یک کران بالا برحسب $$q$$ برای $$|f'|$$ بسازیم.

از تابع $$f$$ مشتق گرفته و به رابطه زیر می‌رسیم.

$$\large f'(E)=e\cos E$$

از آنجایی که $$|\cos E|\leq 1$$، پس خواهیم داشت.

$$\large |f'(E)|\leq e$$

با توجه به نامنفی بودن مقدار $$e$$ قدر مطلق را بر می‌داریم. از طرفی اگر مدار ما بیضوی باشد، خواهیم داشت $$e\leq 1$$ پس نتیجه، حاصل خواهد شد.

$$\large |f'(E)|=\dfrac{|f(E_1)-f(E_2)|}{|E_1-E_2 |}\leq ۱$$

مشخص است که با طرفین وسطین کردن این رابطه می‌توان نوشت:

$$\large |f(E_1)-f(E_2)|\leq |E_1-E_2|$$

اگر در رابطه ۱ مقدار q=1 در نظر گرفته شود، رابطه اخیر، شرایط وجود نگاشت انقباضی را مهیا می‌کند. پس حتما دنباله‌ای از $$\{E_n\}$$ها به یک مقدار ثابت به عنوان پاسخ یا جواب معادله میل می‌کند.

از طرفی چون روش حل این معادله به روش تکراری با قضیه نگاشت انقباضی و نقطه ثابت مطابقت دارد، از همان رابطه‌های ۲ و ۳ که برای پیدا کردن $$x^*$$ استفاده کردیم در اینجا نیز بهره می‌بریم. به این منظور از یک قطعه کد پایتون که در ادامه قابل مشاهده است، برای انجام محاسبات کمک گرفته‌ایم.

1 from math import sin
2
3    M = 3.6029
4    e = 0.37255
5
6    E = M
7    for _ in range(10):
8        E = M + e*sin(E)
9        print(E)

توجه داشته باشید که از کتابخانه math استفاده شده تا محاسبه sin صورت بگیرد. پس از طی ۱۰ مرحله تکرار، پاسخ برای معادله کپلر بدست خواهد آمد.

13.437070
2    3.494414
3    3.474166
4    3.481271
5    3.478772
6    3.479650
7    3.479341
8    3.479450
9    3.479412
10    3.479425

بنابراین مقدار زاویه آنومالی $$E$$ با چهار رقم اعشار صحیح برابر با 3.4794 محاسبه شده است. باید توجه داشت که مقدار $$e$$ در این مثال خیلی بزرگ در نظر گرفته شده. در واقع خروج از مرکز برای سیاره مشتری مقداری حدود 0.05 است. با در نظر گرفتن این مقدار، سرعت همگرایی بسیار سریع‌تر خواهد بود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه‌ی ریاضی و فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های ریاضی و فیزیک
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• معادله های پارامتری — به زبان ساده
• پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
• معادلات و نامعادلات ریاضی — پیدایش و کاربردها
• معادلات خطی (Linear Equations) — به زبان ساده

^^