قوانین ترمودینامیک به زبان ساده
ترمودینامیک در مورد مفاهیمی مانند گرما، دما و تبدل متقابل گرما و دیگر انواع انرژی صحبت میکند. قوانین ترمودینامیک در مورد رفتار این کمیتها توضیح میدهند. قوانین ترمودینامیک، کمیتهای فیزیکی بنیادی مانند انرژی، دما و آنتروپی را تعریف و سیستمهای ترمودینامیکی را در تعادل ترمودینامیکی بررسی میکنند. در این مطلب، قوانین ترمودینامیک را به زبان ساده توضیح میدهیم و در مورد کمیتهایی مانند آنتروپی صحبت میکنیم.
- مفاهیم و قوانین چهارگانه ترمودینامیک را با ساختار مناسب یاد میگیرید.
- نقش انرژی درونی و مسیرهای انتقال انرژی را میآموزید.
- با مفهوم آنتروپی، تفسیر احتمالاتی و ارتباط آن با برگشتناپذیری آشنا میشوید.
- مهارت تحلیل مسائل کاربردی و عددی را بهدست میآورید.
- نحوه استفاده از ترمودینامیک در صنعت و اقتصاد را یاد خواهید گرفت.
- ارتباط قوانین ترمودینامیک با پدیدههای کیهانی و مرگ گرمایی عالم را میآموزید.


قوانین ترمودینامیک چیست ؟
در این مطلب در مورد قوانین ترمودینامیک صحبت میکنیم. قوانین ترمودینامیک مجموعهای از قوانین علمی هستند که گروهی از کمیتهای فیزیکی مانند دما، انرژی و آنتروپی را تعریف میکنند. با استفاده از قوانین ترمودینامیک میتوانیم سیستمهای ترمودینامیکی در تعادل ترمودینامیکی را تحلیل کنیم. همچنین، این قوانین از پارامترهای مختلفی مانند کار و گرمای ترمودینامیکی برای فرایندهای ترمودینامیکی استفاده میکنند. با استفاده از این قوانین میتوان بین کار و گرما رابطه برقرار کرد.
در ابتدا، قوانین ترمودینامیک از سه قانون به نامهای قانون اول، قانون دوم و قانون سوم ترمودینامیک تشکیل میشدند. بعدها، مفهومی بنیادی به نام قانون صفرl ترمودینامیک به این قوانین اضافه شد:
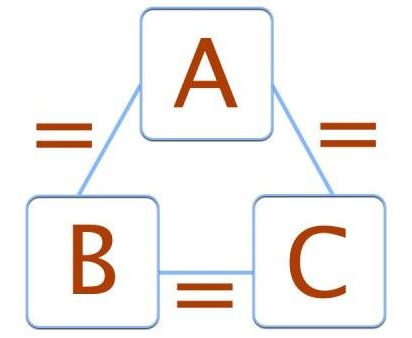
- قانون صفرم ترمودینامیک: بر طبق قانون صفرم از قوانین ترمودینامیک، اگر دو سیستم به نامهای A و B با سیستم سومی به نام C در تعادل ترمودینامیکی باشند، سیستمهای A و B نیز در تعادل ترمودینامیکی با یکدیگر خواهند بود. به بیان دیگر، اگر سیستم A در تعادل ترمودینامیکی با سیستم C و سیستم B نیز در تعادل ترمودینامیکی با سیستم C باشد، سیستمهای A و B نیز در تعادل ترمودینامیکی با یکدیگر قرار دارند.
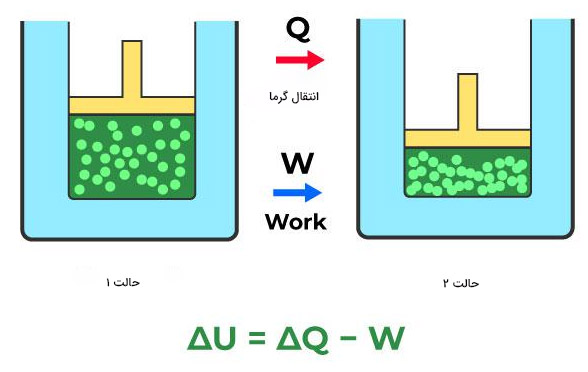
- قانون اول ترمودینامیک: بر طبق اولین قانون از قوانین ترمودینامیک، انرژی میتواند از طریق برهمکنش با گرما، کار و انرژی درونی، از شکلی به شکل دیگر تبدیل شود. توجه به این نکته مهم است که انرژی تحت هیچ شرایطی نمیتواند به وجود بیاید یا از بین برود. بنابراین، قانون اول ترمودینامیک بیاk دیگری از اصل پایستگی انرژی است.
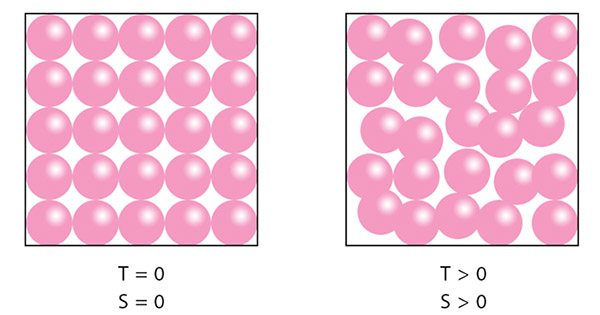
- قانون دوم ترمودینامیک: بر طبق دومین قانون از قوانین ترمودینامیک، آنتروپی کیهان، به عنوان سیستمی ایزوله، همواره با زمان افزایش مییابد. از اینرو، تغییرات آنتروپی در کیهان هرگز نمیتواند منفی باشد.
- قانون سوم ترمودینامیک: سومین و آخرین قانون از قوانین ترمودینامیک به ما اجازه میدهد تا دامنه مطلق آنتروپیها را کمیسازی کنیم. بر طبق این قانون، اگر ساختار کریستالی را با خلوص ۱۰۰٪ در دمای صفر کلوین در نظر بگیریم، آنتروپی آن برابر صفر خواهد بود. به این نکته توجه داشته باشید که اگر ساختار در نظر گرفته شده به طور کامل کریستالی نباشد یا درصد خلوص آن از ۱۰۰ درصد کمتر باشد، آنتروپی آن مخالف صفر خواهد بود.
قوانین ترمودینامیک در جدول زیر به صورت خلاصه بیان شدهاند.
| قانون صفرم ترمودینامیک | اگر و باشد، آنگاه دمای سیستم A نیز با دمای سیستم B برابر خواهد بود. |
| قانون اول ترمودینامیک | اصل پایستگی انرژی، . در این رابطه، U انرژی درونی، Q گرما و W کار هستند. |
| قانون دوم ترمودینامیک | آنتروپی سیستمی بسته با گذشت زمان افزایش مییابد. |
| قانون سوم ترمودینامیک | رسیدن به دمای صفر مطلق امکانپذیر نیست. |
تا اینجا با قوانین ترمودینامیک در حالت کلی آشنا شدیم. در ادامه، هر یک از این قوانین را به زبان ساده توضیح میدهیم.
قانون صفرم ترمودینامیک چیست ؟
ترمودینامیک در رشتههایی مانند فیزیک، شیمی و مهندسی مطالعه میشود. این شاخه از علم تاثیر بسزایی بر رفتار ماده و انرژی در کیهان دارد. گرچه درک مفاهیم ترمودینامیک در نگاه نخست غیرممکن به نظر میرسد، اگر زمان کافی برای مطالعه مفاهیم بنیادی این شاخه از علم صرف کنید، به طور حتم پس از مدتی از مطالعه آن لذت خواهید برد. ترمودینامیک نیز همانند فیزیک نیوتنی یا فیزیک کلاسیک از چند قانون تشکیل شده است. تعداد قوانین ترمودینامیک ابتدا سه قانون بود. سالها بعد، قانون بنیادی دیگری نیز به آن اضافه شد و آن را قانون صفر ترمودینامیک نامیدند. در این بخش، در مورد این قانون صحبت میکنیم.
قانون صفرم ترمودینامیک در مورد تعادل گرمایی صحبت میکند. در تعادل حرارتی، هیچ انتقال گرمایی بین دو سیستمِ در تماس، رخ نمیدهد. قانون صفرم ترمودینامیک میگوید:
اگر دو سیستم A و B با سیستم سومی به نام C در تعادل حرارتی یا گرمایی باشند، سیستمهای A و B نیز با یکدیگر در تعادل حرارتی قرار دارند.
عبارت بالا بسیار واضح به نظر میرسد، اما نباید اهمیت آن را نادیده بگیریم. در واقع، اگر دمای دو جسم یکسان باشد، هیچ انتقال گرمایی بین آنها پس از تماس با یکدیگر، رخ نخواهد داد. بنابراین، از دما میتوان به عنوان شاخص تعادل حرارتی استفاده کرد. اگر دو جسم، در تعادل گرمایی با دو دماسنج مختلف باشند و دماسنجها دمای یکسانی را نشان دهند، دو جسم با یکدیگر در تعادل گرمایی خواهند بود. به هنگام مطالعه ترمودینامیک با برخی تعریفها روبرو و آشنا میشویم.
- سیستم: سیستم از مجموعه اجسامی تشکیل شده است که آنها را بررسی و مطالعه میکنیم. این سیستم توسط محیط اطراف خود احاطه شده است. به عنوان مثال، اگر جعبهای متشکل از گازی مشخص را به عنوان سیستم در نظر بگیریم، بقیه جهان را میتوان به عنوان محیط احاطهکننده جعبه در نظر گرفت. سیستمها به سه دسته تقسیم میشوند:
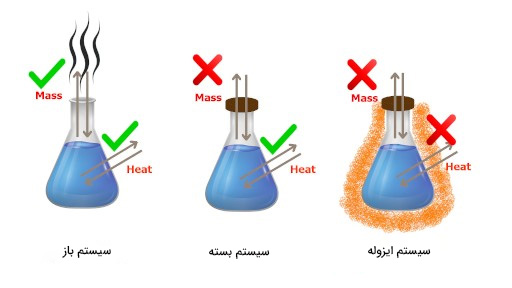
- سیستم باز: در سیستمهای ترمودینامیکی باز، ماده و انرژی میتوانند به سیستم وارد و از آن خارج شوند.
- سیستم بسته: در سیستمهای ترمودینامیکی بسته، ماده نمیتواند به سیستم وارد یا از آن خارج شود. سیستمهای بسته در مقابل عبور انرژی ایزوله نیستند.
- سیستم منزوی: در سیستمهای ترمودینامیکی ایزوله یا منزوی، انرژی و ماده نمیتوانند به سیستم وارد یا از آن خارج شوند.
- دما: به حرکت و ارتعاش اتمها، دما گفته میشود. حرکت اتمها و مولکولها با چشم غیرمسلح دیده نمیشود، اما حرکت آنها سبب میشود که گرمی یا سردی اجسام را حس کنیم.
توجه به این نکته مهم است که هیچ سیستم ترمودینامیکی به طور کامل در برابر عبور گرما ایزوله نیست. اما این فرضیه به هنگام انجام محاسبات ترمودینامیکی برای برخی سیستمها مفید به نظر میرسد.
تعادل گرمایی یا حرارتی را با ذکر مثالی ساده، کمی بیشتر توضیح میدهیم. فرض کنید برشی از کیک تولدتان روی میز قرار دارد. دایره فولادی کوچکی را روی کیک قرار میدهیم. نخستین سوالی که ممکن است به ذهن برسد آن است که گرما بین کیک و دایره فولادی در کدام جهت جریان دارد. گرما از جسمی با دمای بالاتر به جسمی با دمای پایینتر منتقل میشود. برای پیشبرد آزمایش فرض میکنیم برش کیک را چند دقیقه قبل از داخل یخچال بیرون آوردهایم، اما دایره فولادی در محیط اتاق بوده است. بنابراین، دمای برش کیک کمتر از دایره فولادی خواهد بود. از اینرو، گرما از دایره فولادی به برش کیک منتقل میشود.
آیا جریان گرما از دایره فولادی به کیک تا بینهایت ادامه مییابد؟ خیر، انتقال گرما پس از مدت زمان مشخصی متوقف میشود. در این زمان، دایره فولادی به اندازه کافی به کیک گرما داده است. در نتیجه، هیچ گرمای خالصی بین دایره فولادی و کیک منتقل نمیشود. هنگامی که هیچ گرمای خالصی بین دو جسم در تماس منتقل نمیشود، آن دو جسم در تعادل گرمایی با یکدیگر هستند. در قانون صفرم ترمودینامیک، جسم سومی نیز باید وارد شود. به همین دلیل ظرف آبی را به سیستم دو جسمی دایره فولادی و کیک اضافه میکنیم و آن را در تماس با دایره فولادی قرار میدهیم. برای راحتی کار فرض میکنیم ظرف آب و دایره فولادی در تعادل گرمایی با یکدیگر قرار دارند. بنابراین، هیچ گرمای خالصی بین آنها مبادله نمیشود.
به لحظه جالبی رسیدیم. کیک با دایره فولادی در تعادل گرمایی بود و هیچ گرمای خالصی بین آنها مبادله نمیشد. در ادامه، ظرف آب وارد داستان شد و دایره فولادی با آن نیز در تعادل گرمایی قرار داشت. آیا میتوان نتیجه گرفت که ظرف آب با کیک در تعادل گرمایی هستند؟ بله، ظرف آب و برش کیک در تعادل گرمایی با یکدیگر قرار دارند و هیچ گرمای خالصی بین آنها مبادله نمیشود. در اینجا، بار دیگر به قانون صفرم ترمودینامیک سلام میکنیم. این قانون در جهانی که زندگی میکنیم به خوبی برقرار است. اکنون، جهانی را فرض کنید که در آن قانون صفر ترمودینامیک برقرار نیست. چه اتفاقی رخ میدهد؟
در جهان جدید باز هم برش کیک، ظرف آب و دایره فولادی داریم. در این جهان نیز دایره فولادی و برش کیک با یکدیگر در تعادل حرارتی قرار دارند. به طور مشابه، ظرف آب و دایره فولادی نیز در تعادل گرمایی با یکدیگر هستند و هیچ گرمای خالصی بین آنها مبادله نمیشود. آیا ظرف آب و کیک فولادی در تعادل گرمایی با یکدیگر قرار دارند؟ خیر، در این جهان ظرف آب و کیک در تعادل گرمایی با یکدیگر نیستند. در این حالت، گرما از ظرف آب به برش کیک یا از برش کیک به ظرف آب منتقل میشود. این جهان، جهان خوبی برای زندگی و مطالعه فیزیک نخواهد بود، زیرا در این حالت باید تعریف جداگانهای برای دما داشته باشیم و این تعریف به نوع ماده مورداستفاده وابسته است. جهانی که اکنون در آن زندگی میکنیم چنین رفتاری را از خود نشان نمیدهد. جهان ما از قانون صفرم ترمودینامیک پیروی میکند.
این قانون به ما اجازه میدهد مقیاس دما را به صورت جهانی تعریف کنیم. هنگامی که دو جسم در تعادل حرارتی با یکدیگر قرار دارند، دمای آنها یکسان خواهد بود. با استفاده از قانون صفرم ترمودینامیک به راحتی میتوانیم بگوییم دمای برش کیک، دایره فولادی و ظرف آب با یکدیگر برابر هستند. با توجه به آنکه دمای این سه جسم با یکدیگر برابر است، هر کدام از آنها را انتخاب و در تماس با جسم دوم قرار دهیم، هیچ گرمای خالصی بین آنها مبادله نخواهد شد. اگر قانون صفرم ترمودینامیک برقرار نبود، قادر به انجام این کار نبودیم. در اینجا، اهمیت این قانون مشخص میشود.
تا اینجا با قانون صفرم از قوانین ترمودینامیک آشنا شدیم. در ادامه، در مورد اولین قانون از چهار قوانین ترمودینامیک صحبت میکنیم.
قانون اول ترمودینامیک چیست ؟
تا اینجا میدانیم قانون صفرم از قوانین ترمودینامیک در مورد تعادل گرمایی بین سه جسم و دما صحبت میکند. در این بخش، در مورد قانون اول ترمودینامیک و ارتباط آن با انرژی درونی، گرما و کار توضیح میدهیم. ایده بنیادی قانون اول ترمودینامیک چیست؟ این قانون، بیان دیگری از اصل پایستگی انرژی است. بر طبق این اصل، انرژی نه به وجود میآید، نه از بین میرود، بلکه از حالتی به حالت دیگر تبدیل یا از مکانی به مکان دیگر منتقل میشود.
سیستم دلخواهی را به شکل زیر در نظر بگیرید.
سیستم را به گونهای انتخاب میکنیم که انرژی بتواند به آن وارد یا از آن خارج شود. انرژی از دو طریق میتواند این کار را انجام دهد:
- گرما
- کار
اگر گرما به سیستم وارد شود، سیستم انرژی بهدست میآورد. به این انرژی، انرژی درونی سیستم میگوییم و آن را با U نشان میدهیم. همچنین، محیط اطراف میتواند روی سیستم کار انجام دهد. بنابراین، انرژی درونی سیستم با این دو روش افزایش مییابد:
- انتقال گرما به سیستم
- انجام کار روی سیستم
فرض کنید محیط اطراف، ۳۰۰ ژول کار روی سیستم انجام میدهد. بنابراین، انرژی داخلی سیستم به اندازه ۳۰۰ ژول افزایش مییابد. از اینرو، تغییرات انرژی درونی سیستم مثبت خواهد بود:
چه اتفاقی برای انرژی محیط اطراف میافتد؟ انرژی آن به اندازه ۳۰۰ ژول کاهش مییابد. بنابراین، انرژی نه به وجود آمد، نه از بین رفت، بلکه از محیط اطراف به سیستم منتقل شد. سیستم نمیتواند خودبهخود انرژی به اندازه ۳۰۰ ژول تولید کند و انرژی داخلی خود را افزایش دهد. این انرژی باید از جای دیگری به آن منتقل شده باشد. راه دیگر برای درک بهتر انرژی درونی، استفاده از مثال پول است. فرض کنید لپتاپ نسبتا نویی دارید و میخواهید آن را به قیمت ۳۰ میلیون تومان بفروشید. یکی از دوستانتان آن را با این قیمت از شما میخرد. در این حالت، حساب بانکی شما به اندازه ۳۰ میلیون تومان افزایش مییابد. در مقابل، حساب بانکی دوستتان به همین میزان کاهش خواهد یافت. بنابراین، پول از حساب دوست شما به حساب شما منتقل میشود.

پول از ناکجاآباد به حساب شما واریز نشده است. در نتیجه، برای آنکه ۳۰ میلیون تومان بهدست آورید، فرد دیگری باید این مقدار پول را از دست بدهد. در این مثال ساده، پول خلق نشده، بلکه از حسابی به حساب دیگر منتقل شده است. انرژی نیز از اصل مشابهی پیروی میکند. اگر سیستم انرژی برابر ۵۰۰ ژول از دست بدهد، انرژی درونی آن به همین اندازه کاهش مییابد. در مقابل، این مقدار انرژی به محیط اطراف سیستم منتقل میشود و انرژی درونی آن ۵۰۰ ژول افزایش مییابد. از این رو، قانون اول ترمودینامیک بیان دیگری از قانون بقای انرژی است.
در مطالب بالا گفتیم سیستمهای ترمودینامیکی به سه گروه سیستمهای باز، بسته و ایزوله تقسیم میشوند و با ویژگیهای هر یک از آنها آشنا شدیم. تغییرات انرژی درونی سیستم با استفاده از رابطه زیر بهدست میآید:
این معادله را در بسیاری از کتابهای شیمی مشاهده میکنیم. نشاندهنده مقدار گرمای وارد شده یا خارج شده از سیستم است. همچنین، کار انجام شده روی سیستم یا انجام شده توسط سیستم را نشان میدهد. این معادله در فیزیک اندکی متفاوت است و به شکل زیر نوشته میشود:
سوالی که ممکن است مطرح شود آن است که چرا معادله حاکم بر قانون اول ترمودینامیک به این دو صورت نوشته میشود. این تفاوت به دیدگاه انتخاب شده توسط دانشمندان مربوط میشود. در شیمی، دیدگاه سیستمی و در فیزیک و مهندسی، دیدگاه محیط اطراف سیستم انتخاب شده است. به دلیل انتخاب دیدگاه سیستمی در شیمی باید به دو نکته زیر دقت کنیم:
- کار انجام شده توسط سیستم روی محیط، منفی در نظر گرفته میشود. سیستم برای انجام کار باید انرژی مصرف کند. بنابراین، انرژی درونی آن کاهش مییابد. فرض کنید برای ورزش به باشگاه میروید. به هنگام بلند کردن وزنه، بدن انرژی میسوزاند. از اینرو، انرژی درونی بدن کاهش مییابد یا به اصطلاح بدن کالری میسوزاند. در این حالت، کار توسط سیستم انجام شده است. با بلند کردن وزنهها از روی زمین، انرژی پتانسیل آنها را افزایش میدهیم، اما انرژی درونی بدن ما کاهش مییابد.
- در مقابل، کار انجام شده روی سیستم توسط محیط اطراف آن، مثبت در نظر گرفته میشود.

دیدگاه انتخاب شده در فیزیک، دیدگاه محیط محور است. از اینرو:
- کار انجام شده روی سیستم توسط محیط اطراف آن، منفی در نظر گرفته میشود.
- کار انجام شده توسط سیستم روی محیط، مثبت در نظر گرفته میشود.
در ادامه، هر یک از حالتهای بیان شده را توضیح میدهیم. در شیمی، هنگامی که سیستم روی محیط اطراف خود کار انجام میدهد، انرژی درونی آن کاهش مییابد. از آنجا که انرژی سیستم کاهش مییابد، کار منفی است. به یاد داشته باشید که در شیمی دیدگاه سیستمی انتخاب شده است. در فیزیک، دیدگاه انتخاب شده، دیدگاه محیطی است. در نتیجه، هنگامی که کار توسط سیستم انجام میشود، انرژی درونی سیستم هنوز هم کاهش مییابد. اما در این حالت میگوییم کار انجام شده، مثبت است، زیرا محیط انرژی بهدست آورده است و توجه در فیزیک روی محیط است، نه سیستم. به همین دلیل، معادلات نوشته شده در فیزیک و شیمی با یکدیگر تفاوت دارند. در ادامه با انتخاب دیدگاه سیستمی، توضیحات بیشتری در مورد قانون اول ترمودینامیک در شیمی میدهیم. این انتخاب کاملا سلیقهای است و شما میتوانید بسته به کاری که میخواهید انجام دهید، هر یک از دو دیدگاه را انتخاب کنید.
با انتخاب دیدگاه سیستمی، معادله قانون اول ترمودینامیک به صورت زیر نوشته میشود:
هرگاه سیستم (واکنشدهندهها و محصولات واکنش) انرژی گرمایی را جذب کند، مثبت خواهد بود. به بیان دیگر، هرگاه گرما وارد سیستم شود، انرژی گرمایی توسط سیستم جذب و مثبت میشود. به این فرایند، فرایند گرماگیر میگوییم. هرگاه انرژی گرمایی از سیستم خارج شود یا سیستم انرژی گرمایی از دست بدهد، منفی خواهد بود. به این فرایند، فرایند گرماده میگوییم. بنابراین، در فرایندهای گرماگیر، مثبت و در فرایندهای گرماده، منفی است. همچنین، همانطور که گفته شد هنگامی مثبت است که کار روی سیستم انجام شود. در مقابل، اگر سیستم کار انجام دهد، منفی خواهد بود.
در فیزیک، معادله قانون اول ترمودینامیک به صورت زیر نوشته میشود:
انرژی درونی، گرما و کار در معادله بالا برحسب ژول اندازه گرفته میشوند. بر طبق این قانون، فرایندهای ترمودینامیکی متفاوتی ممکن است رخ دهند. در ادامه، در مورد آنها صحبت میکنیم.
فرایندهای ترمودینامیکی
فرایندهای ترمودینامیکی به چند دسته تقسیم میشوند:
- فرایند همحجم
- فرایند همدما
- فرایند بیدررو یا آدیاباتیک
- سیستم منزوی یا ایزوله
فرایند هم حجم چیست ؟
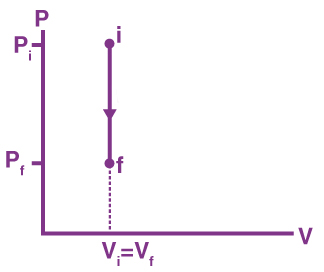
اگر در فرایند ترمودینامیکی حجم سیستم در شروع و پایان فرایند ثابت بافی بماند، به آن فرایند همحجم گفته میشود. در این حالت، کار انجام شده روی سیستم یا کار انجام شده توسط سیستم برابر صفر خواهد بود:
با قرار دادن مقدار در معادله به رابطه زیر میرسیم:
بنابراین، هر تغییری در انرژی درونی به دلیل ورود یا خروج گرما رخ میدهد. کالریمتر بمبی، مثالی از فرایند همحجم است. از این کالریمتر برای تعیین تبادل انرژی به هنگام واکنش استفاده میشود. این وسیله، گرمای واکنش را در حجم ثابت اندازه میگیرد و گرمای اندازهگیری شده برابر تغییرات انرژی درونی است. در شیمی، تغییرات گرمایی واکنش میتواند در فشار یا حجم ثابت اندازه گرفته شود.
فرایند هم دما چیست ؟
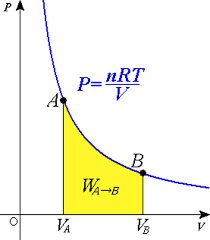
اگر در فرایند ترمودینامیکی، دمای سیستم در شروع و پایان فرایند ثابت باقی بماند، به آن فرایند همدما گفته میشود. در این حالت، تغییرات انرژی درونی سیستم برابر صفر خواهد بود. دلیل صفر شدن انرژی درونی در فرایند همدما رابطه مستقیم انرژی درونی با دما است. در ادامه، رابطه ریاضی این فرایند را بهدست میآوریم. اگر باشد، داریم:
این بدان معنا است که مقداری از انرژی گرمایی وارد شده به سیستم، به انرژی درونی تبدیل نمیشود، بلکه توسط سیستم برای انجام کار استفاده میشود. موتور ایدهآل اتومبیل، مثالی از فرایند همدما است. پیستون داخل موتور، تمام انرژی گرمایی ناشی از واکنش احتراقی را به طور مستقیم به کار تبدیل میکند و سبب حرکت اتومبیل میشود.
فرایند بی دررو یا آدیاباتیک
اگر در فرایند ترمودینامیکی، هیچ تبادل گرمایی صورت نگیرد، مقدار برابر صفر خواهد بود. مقدار را در معادله برابر صفر قرار میدهیم. بنابراین، انرژی درونی برابر منفی کار است:
رابطه فوق بدان معنا است که انرژی درونی سیستم به دو دلیل تغییر میکند:
- سیستم روی محیط اطرافش کار انجام دهد.
- محیط اطراف روی سیستم کار انجام دهد.
به این فرایند، فرایند آدیاباتیک یا بیدررو گفته میشود.
اگر مقدارهای و برابر صفر باشند، هیچ تبادل گرمایی و کار انجام شدهای وجود نخواهد داشت. بنابراین، تغییرات انرژی درونی سیستم برابر صفر خواهد بود. به چنین سیستمی، سیستم ایزوله یا منزوی گفته میشود.
از معادله در بسیاری از مسئلههای ترمودینامیکی برای محاسبات استفاده میشود. به هنگام حل مسئلههای ترمودینامیکی باید مطمئن باشیم که علامت و درست انتخاب شدهاند. به عنوان مثال، فرض کنید کاری به اندازه ۱۰۰ ژول روی سیستم انجام و سیستم فشرده میشود. در نتیجه، انرژی درونی سیستم به اندازه ۷۴ ژول افزایش مییابد. چه مقدار انرژی به شکل گرما و در چه جهتی منتقل شده است؟ برای حل این مثال ساده، گامهای زیر را به ترتیب طی میکنیم:
گام اول
برای حل این مثال، ابتدا باید فرمول مناسب را بنویسیم. در صورت مثال از عبارتهای انرژی درونی، گرما و کار استفاده شده است. بنابراین، بهترین فرمول، فرمول قانون اول ترمودینامیک است:
گام دوم
از آنجا که در این مثال باید مقدار گرمای مبادله شده و جهت آن را پیدا کنیم، رابطه بالا را برحسب مرتب میکنیم:
گام سوم
انرژی درونی سیستم به اندازه ۷۴ ژول افزایش یافته است، بنابراین مقدار آن مثبت خواهد بود.
گام چهارم
علامت کار چیست؟ با توجه به آنکه کار روی سیستم انجام شده است، علامت آن منفی خواهد بود. بنابراین، داریم:
مقدار منفی بهدست آمد. این بدان معنا است که با انجام ۱۰۰ ژول کار روی سیستم، ۷۴ ژول از آن صرف بالا بردن انرژی درونی سیستم میشود و ۲۶ ژول از ۱۰۰ ژول کار انجام شده به شکل گرما از سیستم خارج میشود (انرژی اتلافی). به مثال دیگری در این مورد توجه کنید.
مثال محاسبه گرمای مبادله شده بین سیستم و محیط اطراف
گازی به اندازه ۱۵۰ ژول کار روی محیط اطرافش انجام میدهد و انرژی درونی آن به اندازه ۹۰ ژول کاهش مییابد. مقدار گرمای جذب شده یا از دستداده شده توسط گاز را محاسبه کنید.
پاسخ
از معادله برای حل این مثال استفاده میکنیم. از آنجا که مقدار گرمای مبادله شده بین گاز و محیط اطراف را باید بهدست آوریم، معادله را برحسب Q مینویسیم:
با توجه به مثال، گاز به اندازه ۱۵۰ ژول کار روی محیط اطرافش انجام داده است. با توجه به آنکه سیستم روی محیط اطراف کار انجام داده است، علامت کار مثبت خواهد بود. همچنین، انرژی درونی سیستم به اندازه ۹۰ ژول کاهش یافته است، بنابراین علامت آن را باید منفی در نظر بگیریم:
علامت مثبت به دست آمد، بنابراین گاز به اندازه ۶۰ ژول گرما از محیط جذب کرده است.
نکته: قانون اول ترمودینامیک بیان دیگرِ اصل پایستگی انرژی است. بر طبق این اصل، انرژی نه از بین میرود، نه به وجود میآید، بلکه از حالتی به حالت دیگر تبدیل میشود.
مثال قانون پایستگی انرژی
فرض کنید سنگ کوچکی داریم و آن را با تمام قدرت به سمت بالا پرتاب میکنیم. سنگ تا ارتفاع مشخصی بالا میرود و پس از رسیدن به این ارتفاع سرعت آن برابر صفر میشود. بنابراین، پس از تغییر مسیر به سمت زمین برمیگردد. اگر از مقاومت هوا صرفنظر کنیم، سرعت پرتاب سنگ برابر سرعت رسیدن آن به زمین خواهد بود، اما جهت آنها با یکدیگر متفاوت است. از آنجا که سنگ با سرعت مشخصی از سطح زمین پرتاب شده است، انرژی جنبشی اولیه آن مقدار مشخصی دارد. سرعت سنگ پس از رسیدن به ارتفاعی مشخص برابر صفر میشود. بنابراین مقدار انرژی جنبشی آن نیز در این نقطه برابر صفر خواهد بود.
سوالی که ممکن است مطرح شود آن است که انرژی جنبشی کجا رفته است؟ قانون اول ترمودینامیک به ما میگوید انرژی از بین نمیرود، تولید نمیشود، بلکه از حالتی به حالت دیگر میرود. اینگونه به نظر میرسد که انرژی جنبشی از بین رفته است. اما بر طبق قانون اول ترمودینامیک، انرژی جنبشی، نابود نمیشود، بلکه به شکل دیگری از انرژی تبدیل خواهد شد. در پرتاب سنگ به سمت بالا، انرژی جنبشی به انرژی پتانسیل، تبدیل میشود. بنابراین، پس از رسیدن سنگ به ارتفاع بیشینه، تمام انرژی جنبشی به انرژی پتانسیل تبدیل شده است (مقاوت هوا را نادیده میگیریم).
سوالی که ممکن است مطرح شود آن است که چه اتفاقی به هنگام نادیده نگرفتن مقاومت هوا رخ میدهد؟ در این حالت، توپ با سرعت متفاوتی نسبت به سرعت پرتاب آن به زمین میرسد. اندازه سرعت توپ به هنگام رسیدن به زمین کمتر از سرعت پرتاب آن خواهد بود. بنابراین، مقدار انرژی جنبشی توپ به هنگام پرتاب، بیشتر از مقدار آن به هنگام رسیدن به زمین است. سوالی که ممکن است مطرح شود آن است که چه اتفاقی برای انرژی جنبشی از دست رفته رخ داده است؟ از آنجا که در اینجا مقاومت هوا را نادیده نگرفتهایم، مقداری از انرژی جنبشی اولیه به دلیل وجود مقاومت هوا به گرما تبدیل میشود.

انرژی درونی چیست ؟
در قانون اول ترمودینامیک از عبارتی به نام انرژی درونی سیستم استفاده کردیم. آیا میدانید انرژی درونی سیستم چیست و چگونه اندازه گرفته میشود؟ فرض کنید گازی داخل جعبهای محبوس شده است. تمام دیوارههای گاز، به جز یکی از آنها، ثابت هستند. دیواره متحرک میتواند به سمت بالا و پایین حرکت کند و حجم گاز را تغییر دهد. انرژی درونی برابر تمام انرژیهای داخل سیستم است:
- انرژی جنبشی تمام اتمها و مولکولهای تشکیلدهنده سیستم
- شکلهای دیگر انرژی مانند انرژی چرخشی مولکولها، انرژی مربوط به پیوندهای شیمیایی، انرژی پتانسیل الکتریکی (در صورتی که سیستم فلزی یا نیمهفلزی باشد) و انرژی ارتعاشی.
اگر سیستم جامد یا مایع باشد، اتمها و مولکولهای زیادی در آن وجود دارند. بنابراین، بهدست آوردن انرژی درونی آنها بسیار پیچیده است. برای سادگی سیستم را گاز ایدهآل و در حالت سادهتر، گاز ایدهآل تک اتمی (گاز هلیوم) در نظر میگیریم. اگر عملی روی سیستم انجام شود یا سیستم عملی روی محیط اطراف خود انجام دهد، انرژی درونی آن تغییر میکند. در مطالب بالا دیدیم تغییرات انرژی درونی در فیزیک به صورت تفاضل انرژی گرمایی و کار تعریف میشود.
رابطه بین انرژی درونی، گرما و کار را به صورت زیر نیز میتوان نوشت:
سوالی که ممکن است مطرح شود ان است که این رابطه چه تفاوتی با رابطه یا دارد. در سیستم انتخاب شده مقداری گرما داریم. پس از گذشت مدت زمان مشخصی، مقدار گرمای داخل سیستم تغییر میکند. تفاوت گرمای داخل سیستم را در بازه زمانی داده شده بهدست میآوریم و آن را با نشان میدهیم. بنابراین، گرما حالت ماکروسکوپی ذاتی سیستم است. برای بهدست آوردن مقدار گرمای داخل سیستم به مولکولها و اتمهای آن نگاه نمیکنیم. انرژی درونی، فشار، حجم و دما نیز حالتهای ماکروسکوپی سیستم هستند. هیچ اطلاعی از چگونگی رسیدن سیستم به حالت ماکروسکوپی نداریم، اما میدانیم سیستم در این حالت قرار دارد. به عنوان مثال، میدانیم چه مقدار گرما در سیستم وجود دارد یا دمای آن چه مقدار است.
در زندگی روزمره از گرما و دما به جای یکدیگر استفاده میکنیم، اما گرما در ترمودینامیک، انتقال انرژی است. انرژی درونی را میتوان به حساب بانکی تشبیه کرد. ممکن است مقداری پول به حساب بانکی خود واریز کنید یا مقداری پول از آن برداشت کنید. بنابراین، مقدار پول کلی داخل حساب تغییر خواهد کرد. گرما و کار نیز شبیه انتقال یا برداشت پول هستند. در مطالب بالا گفتیم انرژی داخلی سیستم مجموع انرژیهای مختلف داخل سیستم است. گفتیم محاسبه انرژی بیشتر سیستمها بسیار پیچیده است. بنابراین، در بیشتر موارد سیستم را متشکل از مولکولهای گازی تک اتمی در نظر میگیریم. در ادامه، انرژی درونی این سیستم ساده شده را بهدست میآوریم.
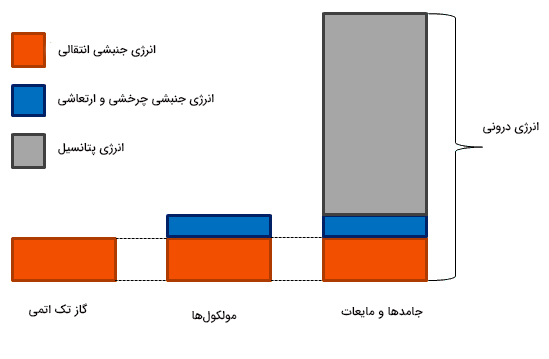
انرژی درونی گاز ایده آل تک اتمی
سیستمی متشکل از اتمهای گاز ایدهآل تک اتمی در نظر بگیرید. در این حالت، انرژی جنبشی اتمهای تشکیلدهنده گاز، تنها انرژی درون سیستم است. در این بخش، انرژی درونی این سیستم را در فشار، دما یا حجم مشخصی بهدست میآوریم. در واقع، رابطه بین انرژی درونی را با این سه کمیت محاسبه میکنیم. مکعبی سهبعدی را به طول در نظر میگیریم و N ذره داخل آن قرار میدهیم. در سیستم عادی، ذرات پس از برخورد به دیوارهها یا پس از برخورد با ذرات دیگر تغییر مسیر میدهند. برای آنکه محاسبه انرژی درونی سیستم در نظر گرفته شده راحتتر باشد، فرض دیگری را نیز در نظر میگیریم.
- یک سوم ذرات در راستای محور حرکت میکنند.
- یک سوم ذرات در راستای محور حرکت میکنند.
- یک سوم ذرات در راستای محور حرکت میکنند.
چنین اتفاقی در واقعیت رخ نمیدهد، اما با این فرضیه، محاسبات ریاضی بسیار سادهتر میشوند.
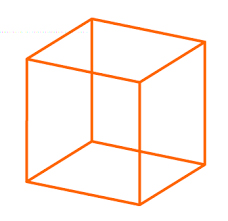
یک وجه از مکعب را به همراه یک ذره به جرم m به صورت نشان داده شده در تصویر زیر در نظر بگیرید. فرض کنید ذره با سرعت حرکت میکند. این ذره یکی از N ذره داخل سیستم است. در ادامه، مقدار فشار وارد شده از طرف ذره بر دیواره مکعب را بهدست میآوریم. مساحت دیواره برابر است. نیروی وارد شده از سمت ذره بر دیواره چه مقدار است؟ ذره به صورت رفت و برگشتی حرکت میکند، بنابراین نیروی وارد شده به دیواره به دلیل تغییر تکانه ذره وارد میشود.
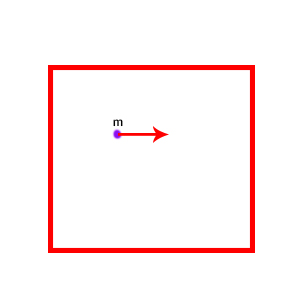
تغییرات تکانه ذره انتخاب شده چه مقدار است؟ تکانه ذره قبل از برخورد به ذره برابر است. ذره پس از برخورد به دیواره، برمیگردد. تکانه آن پس از برخورد به دیوار چه مقدار است؟ اگر برخورد ذره به دیوار کشسان باشد، بدون تغییر سرعت در جهت مخالف شروع به حرکت میکند. بنابراین، تکانه پس از برخورد به دیوار برابر خواهد بود. در نتیجه، تغییرات تکانه ذره برابر است با:
تغییرات تکانه بر واحد زمان برابر است با:
سوالی که ممکن است مطرح شود آن است که این اتفاق در چه بازه زمانی رخ میهد. این اتفاق پس از برخورد کشسان هر ذره به دیواره و بازگشت آن رخ خواهد داد. فاصله زمانی بین برخوردها چه مقدار است؟ فاصله بین دیوارههای روبرو از یکدیگر برابر است. ذره پس از برخورد به دیواره، تغییر مسیر میدهد و پس از طی کردن مسافت به دیواره روبرو برخورد میکند. در ادامه، پس از برخورد با دیواره دوم و طی کردن مسیر به دیواره اول برخورد خواهد کرد. بنابراین، ذره پس از برخورد اول به دیواره و طی کردن مسیر برای بار دوم به آن برخورد میکند. مدت زمان لازم برای طی کردن این مسافت چقدر است؟
بنابراین، تغییرات تکانه برحسب زمان برابر است با:
رابطه بالا، نیروی وارد شده بر دیواره را از طرف یک ذره به ما میدهد. فشار، به صورت نسبت نیرو بر مساحت سطح موردنظر تعریف میشود. از این رو، فشار وارد شده بر دیواره برابر است با:
فشار بهدست آمده از طرف یک ذره بر دیواره را بهدست آوردیم. سیستم ما از N ذره تشکیل شده است. چه کسری از این ذرات پس از برخورد به دیواره موردنظر، منعکس میشوند؟ در مطالب بالا فرض کردیم یک سوم ذرات در راستای محور ، یک سوم در راستای محور ، و یک سوم در راستای محور حرکت میکنند. بنابراین، یکسوم ذرات داخل جعبه به دیواره موردنظر برخورد میکنند. در نتیجه، فشار کل وارد شده بر دیواره، از طرف یکسوم ذرات داخل جعبه خواهد بود و مقدار آن برابر است با:
با ضرب طرفین رابطه بالا در ۳ داریم:
طرفین رابطه بهدست آمده را بر دو تقسیم میکنیم:
انرژی جنبشی یک ذره داخل جعبه است. در رابطه بهدست آمده، انرژی جنبشی در N، تعداد ذرات، ضرب شده است. شاید از خود بپرسید آیا تمام ذرات داخل جعبه انرژی جنبشی یکسانی دارند. بله، زیرا فرض کردیم تمام ذرات با سرعت یکسانی حرکت میکنند. در حالت واقعی، ذرات گاز محبوس شده داخل جعبه ممکن است سرعتهای بسیار متفاوتی داشته باشند. بنابراین، برابر انرژی جنبشی کل سیستم است. از آنجا که گاز داخل جعبه را گازی تک اتمی فرض کردیم، انرژی درونی کل، برابر انرژی جنبشی ذرات داخل سیستم است.
از آنجا که تنها فشار وارد شده بر یک دیواره از شش دیواره را بهدست آوردیم، به احتمال زیاد از خود پرسیدهاید فشار وارد شده بر تمام دیوارهها چه مقدار است. فشار وارد شده بر دیوارهها با یکدیگر برابر هستند. از آنجا که گاز محبوس شده داخل جعبه، گاز ایدهآل است، رابطه حاکم بر آن برابر است با:
در رابطه بالا:
- تعداد مولهای گاز است.
- ثایت جهانی گازها است.
- دما برحسب کلوین است.
با جایگزینی با در رابطه & داریم:
به رابطه جالبی رسیدیم. با داشتن فشار و حجم یا دما و تعداد مولکولهای گاز، به راحتی میتوانیم انرژی درونی سیستم را به دست آوریم. اگر دمای سیستم و تعداد ذرات تغییر نکند، انرژی درونی سیستم نیز ثابت باقی میماند. در مقابل، اگر تغییرات انرژی درونی سیستم مخالف صفر باشد، تغییرات دما نیز مخالف صفر خواهد بود. توجه به این نکته مهم است که در رابطه ، کمیت میکروسکوپی مانند انرژی جنبشی به کمیتهای ماکروسکوپی مانند دما مربوط شده است.
تاکنون از عبارتهایی مانند حالتهای میکروسکوپی و ماکروسکوپی استفاده کردهایم. آیا میدانید مفهوم آنها چیست. در ادامه، برای آشنایی بیشتر با این دو مفهوم، آنها را با جزییات بیشتری توضیح میدهیم.
حالت های میکروسکوپی و ماکروسکوپی چیست ؟
در مطالب بالا از کمیتهایی مانند دما، فشار، حجم، انرژی جنبشی، سرعت و نیرو استفاده کردیم. کمیتهایی مانند فشار، دما و حجم، ویژگیهای سیستم را به ما میدهند و حالتهای ماکروسکوپی سیستم موردنظر هستند. به عنوان مثال، بادکنکی را به صورت زیر در نظر بگیرید. کمیتهای ماکروسکوپی نامبرده را میتوان به آن نسبت داد. مقدار فشار داخل بادکنک برابر P، دمای آن برابر T و حجم آن برابر است.

افراد قبل از آنکه نظری در مورد اتم و تعریف آن داشته باشند، کمیتهای ماکروسکوپی را میشناختند و فشار یا دمای سیستم را اندازه میگرفتند. همانطور که در مطالب بالا گفتیم فشار به دلیل برخورد ذرات داخل سیستم با دیوارههای آن ایجاد میشود. همچنین، دما را به صورت متوسط انرژی جنبشی ذرات داخل سیستم تعریف میکنیم. با دانستن دما، فشار و حجم سیستم، آن را در مقیاس ماکروسکوپی توصیف میکنیم.
اکنون با دانستن تعریف مولکولها و اتمها میتوانیم تعریف دقیقتری از این کمیتهای ماکروسکوپی ارائه کنیم. ویژگیهای هر یک از اتمها و مولکولهای داخل گاز را میتوانیم در هر لحظه از زمان، بنویسیم. به عنوان مثال، تکانه و موقعیت مکانی اتم شماره یک یا اتم شماره دو را در زمان صفر، مینویسیم. توجه به این نکته مهم است تعداد زیادی اتم و مولکول داخل سیستم وجود دارند. به جای نوشتن لیستی بلند بالا از اتمها و ویژگیهای آنها، حالت آنها را در سیستم مینویسیم. در این صورت، حالت میکروسکوپی بادکنک را در زمان صفر داریم.
اگر سیستم در تعادل ترمودینامیکی باشد، حالتهای ماکروسکوپی تغییر نمیکنند. در زمان صفر، حالتهای میکروسکوپی اتمهای مختلف را داریم. پس از گذشت مدت زمانی مشخص، حالتهای میکروسکوپی به طور کامل تغییر میکنند، زیرا ذرات داخل سیستم به طور پیوسته به یکدیگر برخورد میکنند و تکانه یا انرژی خود را به ذرات مجاور منتقل میکنند. گرچه سیستم در حالت تعادل ترمودینامیکی قرار دارد و حالت ماکروسکوپی آن ثابت است، حالتهای میکروسکوپی در بازههای زمانی بسیار کوتاه، به سرعت تغییر میکنند. بنابراین، در ترمودینامیک تمایل داریم از حالتهای ماکروسکوپی به جای میکروسکوپی استفاده کنیم.
در مطالب بالا از عبارتی به نام تعادل ترمودینامیکی صحبت کردیم. در ادامه، مفهوم آن را با جزییات بیشتری توضیح میدهیم.
تعادل ترمودینامیکی چیست ؟
لوله استوانهای یا سیلندری را در نظر بگیرید. فرض کنید سقف سیلندر متحرک است و به سمت بالا یا پایین حرکت میکند. بنابراین، حجم استوانه به راحتی تغییر میکند. سیلندر موردنظر را با گاز پر میکنیم. سیلندر به همراه گاز داخل آن را داخل محیط خلأ قرار میدهیم. بنابراین، هیچ ذرهای وجود ندارد. از اینرو، فشار وارد شده بر سقف متحرک سیلندر برابر صفر خواهد بود. ذرات تشکیلدهنده گاز داخل پیستون به طور پیوسته به دیوارههای آن و سقف متحرک برخورد میکنند. برای ثابت نگه داشتن پیستون و خنثی کردن فشار وارد شده از طرف ذرات گاز به آن، تنها کافی است فشاری از طریق خارج بر آن وارد کنیم. اگر این کار را انجام ندهیم، پیستون به سمت بالا حرکت میکند و حجم گاز افزایش مییابد.

برای انجام این کار میتوان از وزنهای سنگین یا سنگی بزرگ کمک گرفت. نیروی اعمال شده توسط وزنه یا سنگ، به طور کامل اثر نیروی اعمال شده توسط گاز را خنثی میکند. نیروی اعمال شده از طرف وزنه بر مساحت خاصی (مساحت پیستون) وارد میشود. بنابراین، فشار وارد شده بر پیستون از سمت وزنه را میتوان به راحتی محاسبه کرد. این فشار، فشار ناشی از گاز را خنثی میکند. فرض کنید نیمی از وزنه را به صورت ناگهانی تبخیر میکنیم. از اینرو، مقدار نیرو یا فشار وارد شده از طرف وزنه به نصف کاهش مییابد. بنابراین، نیروی خارجی وارد شده از طرف وزنه دیگر نمیتواند اثر فشار وارد شده از سمت گاز را خنثی کند. در نتیجه، پیستون به سمت بالا حرکت میکند.
به این نکته توجه داشته باشید که جرم وزنه به سرعت کاهش یافت. از اینرو، حالت پیستون به آهستگی و پیوستگی تغییر نمیکند. ابتدا، پیستون به سرعت به سمت بالا حرکت میکند و حجم گاز افزایش مییابد. سپس، پیستون و وزنه به سمت پایین حرکت میکنند. این حرکت به صورت نوسانی ادامه مییابد. اگر به اندازه کافی صبر کنیم، سیستم به تعادل ترمودینامیکی دیگری میرسد. در این حالت، پیستون ثابت باقی میماند.
- فشار در سراسر گاز یکسان است.
- دما در سراسر گاز یکسان است.
- حجم در موقعیت پایداری قرار میگیرد و ثانیه به ثانیه تغییر نمیکند.
قبل از کاهش جرم پیستون، حالت ماکروسکوپی سیستم را میتوانیم به خوبی تعریف کنیم. پس از کاهش جرم، پیستون شروع به نوسان میکند و پس از مدت زمان مشخصی میایستد. بنابراین، سیستم، بار دیگر به تعادل ترمودینامیکی میرسد. سوالی که ممکن است مطرح شود آن است که اگر وزنه را از روی پیستون برداریم چه اتفاقی رخ میدهد. در این حالت، پیستون به سمت بالا و پایین حرکت ميکند و به حرکت نوسانی خود ادامه میدهد. در این حالت، اندازه فشار بالای پیستون کمتر از اندازه آن، پایین پیستون است. به بیان دیگر، سیستم در حالت تعادل ترمودینامیکی قرار ندارد.
در این حالت، هیچ یک از حالتهای ماکروسکوپی سیستم به خوبی تعریف نشدهاند. به عنوان مثال، در مورد اندازه فشار یا حجم چیزی نمیتوانیم بگوییم. سیستم ثانیهبهثانیه یا میکروثانیه به میکروثانیه، نوسان میکند. این حالت را در نمودار فشار برحسب حجم رسم میکنیم. قرار دادن وزنه روی پیستون را به عنوان حالت اولیه سیستم در نظر میگیریم. پس از تبخیر ناگهانی نصف وزنه و صبر کردن به اندازه کافی، سیستم به حالت ۲ میرسد. کمیتهای ماکروسکوپی سیستم مانند فشار یا دما از حالت یک به دو تغییر کردهاند.
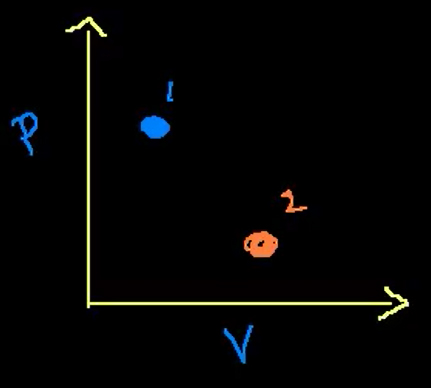
با توجه به نمودار بالا، حالتهای یک و دو را میدانیم، اما هیچ ایدهای در مورد مسیر طی شده بین این دو حالت نداریم. در واقع، مسیر بین دو حالت سیستم مشخص نیست. زیرا فشار و حجم بین این دو حالت تعریف نشدهاند. فشار، حجم و دمای بین دو حالت، تنها هنگامی به طور مشخص تعریف شدهاند که هر حالتی بین دو حالت یک و دو، نزدیک به حالت تعادل ترمودینامیکی باشد.
مثال های قانون اول ترمودینامیک
تا اینجا با اولین قانون از قوانین ترمودینامیک آشنا شدیم. در ادامه تعدادی مثال برای درک بهتر این قانون حل میکنیم.
مثال ۱
اگر ۳۰۰ ژول انرژی گرمایی به سیستمی اضافه شود و سیستم ۲۰۰ ژول کار انجام دهد، انرژی داخلی آن را بهدست آورید.
پاسخ
برای محاسبه انرژی درونی سیستم از رابطه قانون اول ترمودینامیک به صورت زیر استفاده میکنیم:
همانطور که در مطالب بالا گفته شد، انرژی درونی سیستم به دو طریق میتواند تغییر کند:
- گرما از سیستم خارج یا به آن وارد شد.
- سیستم کار انجام دهد یا روی آن کار انجام شود.
اگر مثبت باشد، گرما به سیستم اضافه شده است. در مقابل، اگر منفی باشد، گرما از سیستم خارج میشود. همچنین، اگر مثبت باشد، سیستم کار انجام میدهد. در مقابل، اگر منفی باشد، کار روی سیستم انجام میشود. از آنجا که ۳۰۰ ژول گرما به سیستم اضافه میشود، برابر ژول خواهد بود. بر طبق صورت مثال، سیستم ۲۰۰ ژول کار انجام میدهد، در نتیجه برابر است. بنابراین، انرژی درونی سیستم برابر است با:
در نتیجه، انرژی درونی سیستم به اندازه ۱۰۰ ژول افزایش یافته است.
مثال ۲
اگر۷۰۰ ژول انرژی گرمایی از سیستمی گرفته شود و ۴۰۰ ژول کار روی سیستم انجام دهد، انرژی داخلی آن را بهدست آورید.
پاسخ
انرژی درونی سیستم به صورت زیر تعریف شده است:
در این مثال، ۷۰۰ ژول انرژی گرمایی از سیستم خارج شده است، بنابراین علامت منفی خواهد بود. از آنجا که ۴۰۰ ژول کار روی سیستم انجام شده است، علامت منفی در نظر گرفته میشود. بنابراین، انرژی درونی سیستم برابر است با:
در نتیجه، انرژی درونی سیستم به اندازه ۳۰۰ ژول کاهش مییابد.
مثال ۳
۱۵۰۰ ژول انرژی گرمایی به گازی اضافه میشود. حجم گاز در فشارِ ثابت ۴۵۰۰۰ پاسکال از مقدار ۰/۰۲ مترمکعب به ۰/۰۵ مترمکعب افزایش مییابد. مطلوب است:
- مقدار کار انجام شده روی گاز یا توسط گاز.
- تغییرات انرژی داخلی سیستم.
پاسخ
مقدار کار انجام شده در فشار ثابت برابر است با:
توجه به این نکته مهم است که حاصلضرب یک پاسکال در یک مترمربع برابر یک ژول است.
با توجه به مثبت بودن کار انجام شده، کار توسط سیستم روی محیط اطراف انجام شده است. ۱۵۰۰ ژول انرژی گرمایی به سیستم اضافه میشود. بنابراین، علامت مثبت خواهد بود. در ادامه، قسمت ۲ را حل میکنیم. تغییرات انرژی درونی سیستم برابر است با:
با قرار دادن مقدارهای انرژی گرمایی و کار انجام شده در رابطه بالا، داریم:
مثال ۴
۲۵۰۰ ژول انرژی گرمایی از گازی گرفته میشود. حجم گاز در فشارِ ثابت ۳/۰ اتمسفر، از مقدار ۲۵ لیتر به ۱۵ لیتر کاهش مییابد. مطلوب است:
- مقدار کار انجام شده روی گاز یا توسط گاز.
- تغییرات انرژی داخلی سیستم.
پاسخ
مقدار کار انجام شده در فشار ثابت برابر است با:
در این مثال، حجم گارزدر فشار ثابت کاهش یافته است. بنابراین، کار روی سیستم انجام میشود. همچنین، توجه به این نکته مهم است که حاصلضرب یک پاسکال در یک مترمربع برابر یک ژول است. از اینرو، فشار و حجم باید برحسب پاسکال و مترمکعب نوشته شوند.
جواب بهدست آمده را باید به ژول تبدیل کنیم:
۲۵۰۰ ژول انرژی گرمایی از سیستم خارج شده است. بنابراین، علامت منفی خواهد بود. در ادامه، قسمت ۲ را حل میکنیم. تغییرات انرژی درونی سیستم برابر است با:
با قرار دادن مقدارهای انرژی گرمایی و کار انجام شده در رابطه بالا، داریم:
قانون دوم ترمودینامیک چیست ؟
تا اینجا، با اولین قانون از قوانین ترمودینامیک آشنا شدیم. در این بخش، با دومین قانون از قوانین ترمودینامیک آشنا میشویم. قانون دوم ترمودینامیک، قانون عجیبی است و به روشهای مختلفی بیان شده است. یکی از رایجترین بیانهای این قانون به صورت زیر است:
گرما هیچگاه به صورت خودبهخودی از جسم سردتر به جسم گرمتر منتقل نمیشود.
به عنوان مثال، اگر قطعه یخی را داخل ظرف آب گرمی بیندازید، گرما از جسم گرمتر، یعنی آب، به جسم سردتر، یعنی قطعه یخ، منتقل میشود و سبب ذوب شدن آن میشود. سوالی که ممکن است مطرح شود آن است که با توجه به عدم نقض قانونهای فیزیک، مانند قانون بقای انرژی، چرا گرما از جسم سرد به جسم گرم منتقل نمیشود. قبل از پاسخ به این پرسش، کمی در مورد نسخه جایگزین قانون دوم ترمودینامیک صحبت میکنیم:
بینظمی کل سیستم ترمودینامیکی هرگز کاهش نمییابد.
بینظمی چیست؟ اتاقی را فرض کنید که در آن کرههای آبی وجود دارند و به اطراف حرکت میکنند. حرکت کرهها کاملا تصادفی است. همچنین، کرهها پس از برخورد به دیوار هیچ انرژی از دست نمیدهند و بدون تغییر سرعت به حرکت خود ادامه میدهند. علاوه بر کرههای آبی، کرههای قرمز در سمت دیگر اتاق وجود دارند. کرههای قرمزرنگ نیز به صورت تصادفی حرکت میکنند و پس از برخورد به دیوارهها، بدون تغییر سرعت به حرکت خود ادامه میدهند. کرههای آبی و قرمز توسط غشایی از یکدیگر جدا شدهاند. بنابراین، کرهها نمیتوانند با یکدیگر مخلوط شوند. حالت توصیف شده، حالتی منظم است، زیرا کرههای آبی و قرمز از یکدیگر جدا شدهاند.
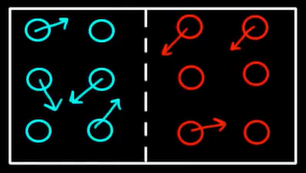
در ادامه، غشای بین کرههای آبی و قرمز را برمیداریم. چه اتفاقی رخ میدهد؟ کرهها با یکدیگر مخلوط میشوند و به اطراف حرکت میکنند. در این حالت، سیستم درجهای از بینظمی را در خود دارد. در اینجا بار دیگر قانون دوم ترمودینامیک تایید میشود. اگر به سیستمی اجازه دهیم کاری را که دوست دارد به صورت خودبهخودی انجام دهد، از حالتی با نظم کمتر به حالتی با نظم بیشتر میرود و هیچ حالت دیگری وجود نخواهد داشت. اگر به اندازه کافی صبر کنیم، هیچگاه قرار گرفتن توپهای آبی در سمتی از اتاق و توپهای قرمز در سمت دیگری از اتاق را نخواهیم دید. اگر تعداد توپها بسیار زیاد باشد، قرار گرفتن آنها به طور منظم در سمتی از اتاق تقریبا برابر صفر است.
در واقع، احتمال این رخداد صفر نیست، اما مقدار آن بسیار کوچک خواهد بود. به بیان دیگر، احتمال رفتن سیستمی نامنظم با تعداد زیادی ذره به حالت منظم، بسیار اندک است. با توجه به مشاهدههای روزانه، احتمال کم بودن وقوع این رخداد را میدهیم. اما سوالی که ممکن است مطرح شود آن است که چرا چنین اتفاقی نمیافتد. اساسا، پاسخ این پرسش به شمارش مربوط میشود. ابتدا، حالت منظم نشان داده شده در تصویر بالا را در نظر بگیرید. تعداد راههای قرار گرفتن توپهای قرمز در کنار هم و توپهای سبز در کنار یکدیگر بسیار زیاد است. اکنون، حالتی را در نظر بگیرید که توپها با یکدیگر مخلوط شدهاند. تعداد راههای پخش شدن توپهای قرمز و سبز در اتاق در این حالت چقدر است؟ تعداد راههای پخش شدن توپها در اتاق در این حالت بسیار زیادتر از تصور ما است.
در حالت منظم، توپهای قرمز در نیمه راست اتاق و توپهای سبز در نیمه چپ اتاق میتوانند جابجا شوند. اما در حالت بینظم، توپهای آبی و قرمز در سراسر اتاق پخش شدهاند و هیچ محدودیت مکانی ندارند. این ایده ساده، پایه و اساس دومین قانون از قوانین ترمودینامیک است. به بیان دیگر، قانون دوم ترمودینامیک به این دلیل برقرار است که تعداد حالتهای بینظم بسیار بیشتر از تعداد حالتهای منظم است. توجه به این نکته مهم است که احتمال قرار گرفتن سیستم در حالت بینظم نشان داده شده در تصویر زیر برابر قرار گرفتن آن در حالت منظم نشان داده شده در تصویر بالا است.
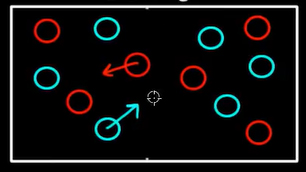
شاید یکسان بودن احتمال قرار گرفتن سیستم در هر یک از دو حالت نشان داده شده در بالا عجیب به نظر برسد. قبل از هر قضاوتی به این نکته توجه داشته باشید که احتمال قرار گرفتن سیستم در حالتهای نشان داده شده یکسان است. نباید فراموش کنیم که تعداد حالتهای بینظم بسیار بیشتر از تعداد حالتهای منظم است. بنابراین، اگر حالت دلخواهی را از میان تمام حالتهای ممکن، منظم یا بینظم، انتخاب کنیم، حالت انتخاب شده با احتمال زیادی، حالت بینظم خواهد بود. اگر تعداد ذرات سیستم بسیار زیاد باشد، احتمال انتخاب حالت بینظم بسیار زیاد است.
برای درک بهتر سیستمهای منظم و بینظم، باید چند عبارت را تعریف کنیم. فیزیکدانها عبارتهایی مانند حالتهای ماکروسکوپی و میکروسکوپی را تعریف کردهاند. در مطالب بالا با مفهوم این دو عبارت آشنا شدیم. حالت ماکروسکوپی به ما میگوید ذرات داخل سیستم با یکدیگر مختلط یا از یکدیگر جدا هستند. در مقابل، حالت میکروسکوپی در مورد جزییات ذرات داخل سیستم و موقعیت دقیق هر ذره، اطلاعات میدهد. اگر بدانیم ذرات با یکدیگر مخلوط شدهاند، لزوما اطلاعی در مورد موقعیت مکانی آنها نداریم.
نکته: تعداد حالتهای میکروسکوپی برای حالت ماکروسکوپی بینظم بیشتر از تعداد حالتهای میکروسکوپی برای حالت ماکروسکوپی منظم است. به همین دلیل، سیستم از حالت منظم به حالت بینظم میرود.
شاید از خود بپرسید رفتن از حالت منظم به حالت بینظم چه ربطی به انتقال گرما از جسم سردتر به جسم گرمتر دارد. به هنگام صحبت در مورد بینظمی، تنها در مورد مکان ذرات صحبت نمیکنیم، بلکه سرعت یا انرژی ذرات داخل سیستم نیز میتوانند بینظم شوند. اتاقی را در نظر بگیرید که از گاز عجیبی پر شده است. در لحظهای مشخص، تمام مولکولهای گاز قرار گرفته در سمت راست اتاق با سرعت بسیار بزرگتری نسبت به مولکولهای گاز قرار گرفته در سمت چپ اتاق حرکت میکنند. بنابراین، اتاق به دو قسمت سرد و گرم تقسیم میشود. در این حالت، سیستم منظم است.
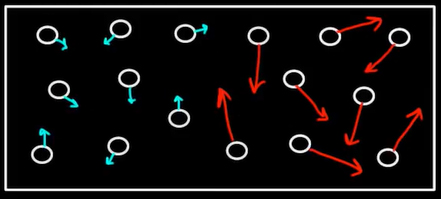
پس از چند لحظه، سیستم نشان داده شده در تصویر بالا از حالت منظم خارج میشود و ذرات با یکدیگر مخلوط میشوند. فرض کنید سمت چپ اتاق و در قسمت سرد آن ایستادهاید. پس از چند لحظه احساس گرما خواهید کرد. زیرا گرما از سمت راست اتاق به سمت چپ آن منتقل میشود. ذرات با سرعت بیشتر به ذرات با سرعت کمتر برخورد میکنند و قسمتی از انرژی خود را به آنها میدهند. به بیان دیگر، انرژی بینظم میشود. انرژی از حالت منظم به حالت بینظم میرود یا توزیع انرژی یکنواخت میشود.
حالت ماکروسکوپی را در نظر بگیرید که در آن مولکولهای گرم از مولکولهای سرد، جدا شدهاند. پس از توزیع انرژی بین مولکولها، حالت ماکروسکوپی داریم که در آن انرژی تقسیم شده و مولکولها با یکدیگر مخلوط شدهاند. تعداد حالتهای میکروسکوپی در حالت اول از تعداد حالتهای میکروسکوپی حالت دوم، کمتر است. به مقدار بینظمی سیستم، آنتروپی گفته میشود و آن را با S نشان میدهیم. یک راهِ دانستن فرمول آنتروپی، نگاه کردن به آرامگاه بولتزمن است. فرمول آنتروپی روی مزار او نوشته شده است.

آنتروپی با استفاده از رابطه زیر بهدست میآید:
در رابطه بالا:
- ثابت بولتزمن است.
- تعداد میکروحالتهای یک حالت ماکروسکوپی خاص است.
آنتروپی کمیتی بسیار جالب و در عین حال پیچیده است. آنتروپی نقش مهمی در آغاز و پایان کیهان دارد. در بخشهای بعد، آنتروپی را به طور کامل توضیح میدهیم.
فرایندهای برگشت پذیر و برگشت ناپذیر چیست ؟
قانون دوم ترمودینامیک در مورد آنتروپی است. آنتروپی را به عنوان معیاری برای اندازهگیری مقدار بینظمی در سیستم ترمودینامیکی، تعریف کردیم. بنابراین، قانون دوم ترمودینامیک به فرایندهای برگشتپذیر یا برگشتناپذیر مربوط میشود. فرایند برگشتپذیر به فرایندی گفته میشود که میتواند پس از تغییر حالت، به حالت اولیه خود بازگردد. مقدار آنتروپی در فرایندهای برگشتپذیر تغییر نمیکند. در مقابل، در فرایندهای برگشتناپذیر، مقدار آنتروپی با گذشت زمان افزایش مییابد.
آنتروپی، تابع حالت است. این کمیت، یک نقطه یا یک حالت را در زمان اندازه میگیرید. مقدار آنتروپی هرگز در سیستمهای بسته کاهش نمییابد. همچنین، آنتروپی کیهان با گذشت زمان افزایش مییابد. افزایش آنتروپی کیهان به چه معنا است؟ دو ویدئو یکسان به نامهای A و B داریم که در هر یک از آنها توپی حرکت میکند. تنها تفاوت دو ویدئو در آن است که در یکی از آنهای توپ به سمت جلو و در دیگری توپ به سمت عقب حرکت میکند.

آیا میدانید کدام ویدئو حرکت توپ را به سمت جلو و کدام حرکت آن را به سمت عقب نشان میدهد؟ پاسخ به این پرسش سخت است. به این مثال میتوان به عنوان فرایندی برگشتپذیر نگاه کرد. احتمال وقوع فرایند در حالت A یا B با یکدیگر برابر است. دو حالت دیگر را در نظر بگیرید. در یکی از حالتها آب از بطری، داخل لیوان ریخته میشود. در دیگری، آب از لیوان به سمت بطری حرکت میکند. کدام فرایند از نظر فیزیکی رخ میدهد؟ ریختن آب از بطری به داخل لیوان. در این حالت، با فرایند برگشتناپذیر مواجه میشویم. ریختن آب از بطری به داخل لیوان با احتمال بالایی رخ میدهد. اما ریختن آب از لیوان به داخل بطری از نظر آماری تقریبا غیرممکن است.

تا اینجا با قانون دوم از قوانین ترمودینامیک یا آنتروپی آشنا شدیم. هر فرایند فیزیکی یا شیمیایی به گونهای رخ میدهد که آنتروپی کل افزایش یابد. فرایندها به دو دسته تقسیم میشوند:
- فرایند برگشتناپذیر: آنتروپی در این فرایند با گذشت زمان افزایش مییابد.
- فرایند برگشتپذیر: آنتروپی در این فرایند با گذشت زمان تغییر نمیکند و ثابت باقی میماند.
تعاریف استاندارد قانون دوم ترمودینامیک چیست ؟
دو تعریف استاندارد برای قانون دوم ترمودینامیک وجود دارد. در این بخش در مورد این تعریفها صحبت میکنیم.
تعریف کلازیوس
بر طبق این تعریف، ساخت موتورِ سیکلی یا چرخهای که تنها کار آن انتقال پیوسته گرما از منبعی با دمای بالاتر به منبعی با دمای پایینتر باشد، غیرممکن است. به بیان سادهتر، ساخت یخچالی که بتواند انرژی را از منبعی با دمای کمتر (منبع سرد) دریافت و به منبع با دمای بالاتر (منبع گرم) انتقال دهد، بدون انجام کار امکانپذیر نیست.
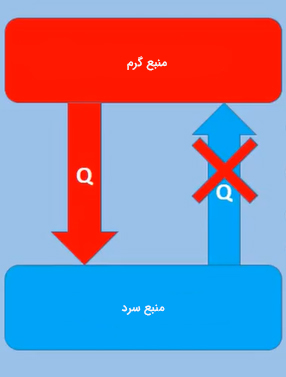
تعریف کلوین-پلانک
بر طبق این تعریف، ساخت موتور گرمایی سیکلی که بتواند کاری برابر گرمای جذب شده از منبع انجام دهد، امکانپذیر نیست. بازده چنین موتوری برابر ۱۰۰ درصد است. به بیان دیگر، ماشین گرمایی نمیتواند تمام انرژی کسب شده از منبع گرمایی در یک چرخه را به کار تبدیل کند، بلکه قسمتی از انرژی دریافت شده از منبع گرم، به شکل انرژی تلف شده به منبع سرد داده میشود. این فرایند در تصویر زیر نشان داده شده است. همانطور که در عکس مشاهده میشود، موتور سیکلی گرمایی برابر از منبع گرم دریافت میکند. موتور، قسمتی از را به شکل کار به محیط اطراف و قسمتی از آن را به شکل انرژی اتلافی به منبع سرد میدهد.
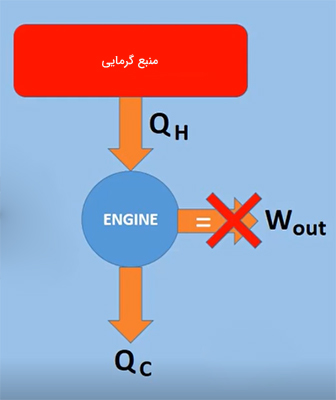
قانون دوم ترمودینامیک به هنگام آزمایشهای دانشمندی به نام «سعدی کارنو» (Sadi Carnot) روی موتورهای گرمایی، مطرح شد. موتور گرمایی، مانند موتور بخار در قرن نوزدهم میلادی، وسیلهای است که با استفاده از گرما، کار انجام میدهد. موتور بخار، گرما را از کوره ذغالسنگ دریافت و بخار تولید میکند. بخار ایجاد شده پیستون متصل به چرخهای قطار و در نتیجه قطار را به حرکت درمیآورد. بنابراین، کار انجام میشود. گرمای اضافی دریافت شده از منبع گرم که کار انجام نمیدهد، به منبع سرد منتقل خواهد شد. به یاد داشته باشید که دمای منبع سرد همواره کمتر از دمای منبع گرم است.
کارنو به این نتیجه رسید که بیشینه کار انجام شده در یک چرخه از موتور گرمایی برابر تفاضل گرمای وارد شده به سیستم و گرمای خارج شده از آن است. بر طبق قانون اول ترمودینامیک، گرمای اتلافی نمیتواند به کار تبدیل شود:
اگر مقدار گرمای اتلافی برابر صفر باشد، تمام گرمای وارد شده به موتور به کار تبدیل میشود. بنابراین، بازده موتور برابر ۱۰۰٪ خواهد بود. همانطور که در مطالب بالا گفتیم، این حالت از نظر فیزیکی به چند دلیل غیرممکن است. یکی از مهمترین دلیلها عبارت است از، تنها راه برای رسیدن به بازده ۱۰۰٪ آن است که هر فرایندی داخل موتور به طور کامل برگشتپذیر باشد. این بدان معنا است که سیستم و محیط اطراف آن بتوانند به حالت اولیه خود بازگردند. به این حالت، اصل کارنو گفته میشود.
از آنجا که آنتروپی مفهوم بسیار جالب و پیچیدهای در ترمودینامیک است، در ادامه در مورد این کمیت و نقش آن در برخی پدیدههای فیزیکی توضیح میدهیم.
آنتروپی چیست ؟
تا اینجا با قانونهای اول و دوم از قوانین ترمودینامیک آشنا شدیم. قانون اول ترمودینامیک در مورد پایستگی انرژی و قانون دوم در مورد آنتروپی است. در این بخش، در مورد آنتروپی صحبت میکنیم. در مطالب بالا گفتیم آنتروپی معیاری از میزان بینظمی داخل سیستم است و همواره افزایش مییابد. بنابراین، آنتروپی کیهان همواره در حال افزایش است. گرچه این تعریف برای آنتروپی توسط بسیاری از افراد پذیرفته شده است، تعریف بهتری برای این کمیت وجود دارد. این تعریف به زمانی بازمیگردد که برای نخستین بار مفهوم آنتروپی بیان شد. اختراع آنتروپی به نحوه عملکرد موتورها و افزایش بازده آنها مربوط میشود.
اگر دو جسم با دماهای متفاوت در تماس با یکدیگر قرار بگیرند، گرما از جسم گرمتر به جسم سردتر منتقل میشود. انتقال گرما تا جایی ادامه مییابد که گرما بین دو جسم به طور یکنواخت توزیع شود. توزیع یکنواخت گرما بین دو جسم نقطه پایان انتقال گرما بین دو جسم است. عکسِ این فرایند رخ نمیدهد. یعنی اگر دو جسم با دمای یکسان، در تماس با یکدیگر قرار داشته باشند و گرما بین آنها به طور یکنواخت پخش شده باشد، هیچ انتقال گرمایی از جسمی به جسم دیگر رخ نمیدهد. یکی از تعریفهای گفته شده برای آنتروپی عبارت است از:
آنتروپی معیاری برای میزان پراکندگی انرژی است.
همانطور که گفتیم آنتروپی همواره در حال افزایش است، بنابراین انرژی همواره گسترش مییابد. انرژی از ترازهای فشرده به ترازهای جدا از هم منتقل میشود. توجه به این نکته مهم است که نمیتوان انرژی را به صورت موضعی در یک جا جمع کرد، مگر آنکه ترازهای انرژی را در قسمت دیگری از هم جدا کرده باشیم. آنتروپی، پدیدهای آماری است. از آنتروپی برای توضیح پدیدههای مختلف استفاده میشود:
- چرا فرایندهای فیزیکی، مسیر مشخصی را طی میکنند و از مسیر دیگری نمیگذرند.
- چرا یخ، ذوب میشود.
- چرا خامه در قهوه پخش میشود.
- چرا هوا از لاستیک پنچر شده بیرون میآید.
تعریف آنتروپی به عنوان معیاری برای اندازهگیری بینظمی سیستم، کمی گمراهکننده است. به عنوان مثال، کدام مورد بینظمتر است، لیوانی پر شده از تکههای یخ یا لیوانی پر شده از آب در دمای اتاق؟ بیشتر افراد لیوان پر شده از تکههای یخ را انتخاب میکنند. این انتخاب اشتباه است، زیرا آنتروپی لیوان پر شده از تکههای یخ، کمتر است.

آنتروپی را میتوان از دیدگاه دیگری بررسی کرد، احتمال. درک مفهوم این دیدگاه در گام نخست مشکل به نظر میرسد، اما کمک شایانی به داشتن درک بهتری از آنتروپی میکند. دو جامد کوچک را در نظر بگیرید. هر یک از این جامدها از شش پیوند شیمیایی تشکیل شدهاند. در هر جامد، انرژی در پیوندهای شیمیایی ذخیره شده است. هر پیوند شیمیایی را میتوان به عنوان ظرفی در نظر گرفت که واحدهای انرژی به نام کوانتا را در خود نگه میدارد. هرچه انرژی جامدی بیشتر باشد، گرمتر است.
گرچه راههای مختلفی برای توزیع انرژی در هر جامد وجود دارند، انرژی کل هر یک از آنها میتواند با یکدیگر برابر باشد. به هر یک از این راهها میکروحالت گفته میشود. برای شش کوانتای انرژی در جامد شماره یک و دو کوانتای انرژی در جامد شماره دو، ۹۷۰۲ میکروحالت وجود دارند. به طور حتم، راههای دیگری برای چیدمان هشت کوانتای انرژی وجود دارند. به عنوان مثال، تمام کوانتاهای انرژی میتوانند در جامد شماره یک باشند و هیچ کوانتایی در جامد شماره دو نباشد.
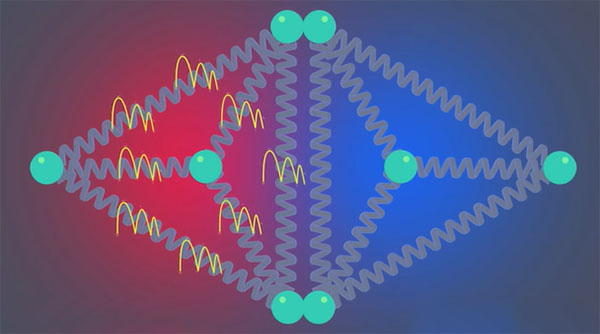
اگر فرض کنیم احتمال وقوع میکروحالتها با یکدیگر برابر باشد، به این نکته پی میبریم که برخی آرایش انرژی احتمال بیشتری نسبت به آرایشهای دیگر دارند. این موضوع به تعداد میکروحالتها در هر آرایش مربوط میشود. آنتروپی، اندازهگیری مستقیم احتمال هر آرایش انرژی است. هر آرایش انرژی که بیشترین گستردگی توزیع انرژی بین دو جامد را داشته باشد، بالاترین آنتروپی یا احتمال را خواهد داشت. آنتروپی کوچک به معنای تمرکز موضعی انرژی و آنتروپی بزرگ به معنای گسترش توزیع انرژی است.
برای آنکه بدانیم چرا آنتروپی برای توضیح فرایندهای خودبهخودی، مانند سرد شدن اجسام داغ، مفید است، باید به سیستمهای دینامیکی یا پویا نگاه کنیم. انرژی در این سیستمها حرکت میکند. در واقعیت، انرژی ساکن نیست و بین ترازهای انرژی حرکت میکند. آرایش انرژی با حرکت انرژی تغییر میکند. به دلیل توزیع میکروحالتها، سیستم با احتمال ۲۱ درصد در حالتی قرار میگیرد که در آن توزیع انرژی بیشینه است. همچنین، سیستم با احتمال ۱۳٪ به نقطه آغاز برمیگردد. جامد شماره یک با احتمال ۸٪ انرژی کسب میکند.
تعداد راههایی که انرژی میتواند توزیع شود و آنتروپی افزایش یابد، بسیار بیشتر از تمرکز موضعی انرژی در نقطهای مشخص در سیستم است. بنابراین، هنگامی که جسمی گرم را کنار جسمی سرد قرار میدهیم، جسم گرم، سردتر و جسم سرد، گرمتر میشوند. حتی در این حالت باز هم ۸ درصد احتمال دارد که جسم گرم، گرمتر و جسم سرد، سردتر شود. چرا این حالت هرگز در زندگی واقعی رخ نداده است؟ پاسخ به این پرسش به اندازه سیستم مربوط میشود.
جامدهای فرضی گفته شده در بالا تنها شش پیوند شیمیایی داشتند. در ادامه، اندازه سیستم را بزرگ میکنیم و تعداد پیوندها را به ۶۰۰۰ و تعداد کوانتاهای انرژی را به ۸۰۰۰ افزایش میدهیم. سیستم را به گونهای آغاز میکنیم که سهچهارم انرژی در جامد یک و یکچهارم انرژی در جامد دو باشد. در این حالت، احتمال آنکه جامد یک به صورت خودبهخودی انرژی بیشتری کسب کند بسیار کوچک میشود. تعداد ذرات تشکیلدهنده اجسام در دنیای واقعی بسیار بیشتر از عددهای گفته شده است. احتمال گرمتر شدن جسمی گرم در دنیای واقعی بسیار کوچک است، به گونهای که اتفاق نمیافتد.
یخ ذوب میشود، خامه با قهوه داغ مخلوط میشود، هوا از لاستیک پنچر خارج میشود، زیرا گسترش توزیع انرژی در این حالتها بسیار بیشتر از حالتهای دیگر است. هیچ نیروی جادویی برای بردن سیستم به آنتروپی بیشتر وجود ندارد. نکته مهم آن است که از نگاه آماری، آنتروپی بیشتر محتملتر است. اگر انرژی شانس توزیع بیشتر داشته باشد، حتما این کار را انجام خواهد داد.

آنتروپی سیاه چاله چیست ؟
سیاهچاله جسمی با جرم، چگالی، و میدان گرانشی بسیار زیاد است، به گونهای که حتی نور نمیتواند از میدان گرانشی قوی آن فرار کند. در واقع مرزی به نام افق رویداد در اطراف سیاهچاله وجود دارد که نور پس از عبور از آن، هیچ راه فراری از دام سیاهچاله نخواهد داشت. در صورت کروی شکل بودن سیاهچاله، میتوانیم برای آن شعاع تعریف کنیم. شعاع سیاهچاله برابر فاصله مرکز آن تا افق رویداد است و با نشان داده میشود. در این بخش، بیشتر به افق رویداد سیاهچاله توجه میکنیم.
کمیت جالبی به نام سرعت فرار را میتوان برای افق رویداد تعریف کرد. برای آنکه هر جسمی بتواند از دام سیاهچاله فرار کند، باید سرعت حرکت آن بیشتر از سرعت فرار باشد. اندازه سرعت فرار بزرگتر از سرعت نور است. به طور حتم با مفهوم سرعت فرار در فیزیک یک دانشگاهی آشنا شدهاید. برای آنکه موشکی بتواند از میدان گرانشی زمین رها شود باید با سرعتی بیشتر از سرعت فرار (در حدود ۱۱۰۰۰ متر بر ثانیه) حرکت کند. اگر سیستم زمین و موشک را در مورد سیاهچاله به کار ببریم، افق رویدادی مرزی است که در آن سرعت فرار برابر سرعت نور میشود.

اگر جسمی از افق رویداد عبور کند و به دام سیاهچاله بیافتد، برای فرار از این دام باید با سرعتی بیشتر از سرعت نور حرکت کند. تا آنجا که میدانیم هیچ جسمی نمیتواند سریعتر از سرعت نور حرکت کند. ینابراین، هر جسمی پس از عبور از افق رویداد، به دام سیاهچاله میافتد. با استفاده از معادلات اینشتین در متریک شوارتزشیلد میتوان به این نتیجه رسید که افق رویداد سیاهچاله غیرچرخشی باید به شکل کره باشد. متریک شوارتزشیلد بهترین مدل ریاضی برای توصیف رفتار سیاهچالههای غیرچرخشی است.
اگر سیاهچاله به شکل کره باشد، نخستین کمیتی که میتوانیم برای افق رویداد سیاهچاله بهدست آوریم سطح مقطع آن خواهد بود. سطح مقطع کره با استفاده از رابطه زیر بهدست میآید:
از آنجا که فاصله مرکز سیاهچاله تا افق رویداد برابر است، سطح مقطع آن برابر است با:
توجه به این نکته مهم است که کروی بودن افق رویداد، چندان مهم نیست، بلکه سطح مقطع آن مهم است. زیرا سطح مقطع افق رویداد به هنگام محاسبه آنتروپی سیاهچاله، اهمیت بالایی دارد. در مطالب بالا گفتیم آنتروپی معیاری از میزان بینظمی در سیستم است. بر طبق قانون دوم ترمودینامیک، آنتروپی کل سیستمی بسته، به عنوان مثال کیهان، تنها میتواند افزایش یابد یا ثابت بماند. آنتروپی هرگز کاهش نمییابد. از آنجا که تمام شواهد و آزمایشهای تجربی انجام شده تاکنون بر درستی قانون دوم ترمودینامیک تاکید دارند، به حقیقت مهمی میرسیم، سیاهچاله باید آنتروپی داشته باشد.

شاید از خود بپرسید اگر آنتروپی سیاهچاله برابر صفر باشد، چه اتفاقی رخ میدهد. فرض کنید جسمی بیرون از سیاهچاله با آنتروپی غیرصفر را به داخل سیاهچاله میاندازیم. اگر آنتروپی سیاهچاله برابر صفر باشد، جسم آنتروپی را با خود به داخل سیاهچاله میبرد و آنتروپی پس از ورود به سیاهچاله از بین میرود. بنابراین، آنتروپی کل کیهان کاهش مییابد. کاهش آنتروپی برخلاف قانون دوم ترمودینامیک است. از اینرو، آنتروپی سیاهچاله نمیتواند برابر صفر باشد. آنتروپی سیاهچاله با استفاده از معادله زیر محاسبه میشود:
در رابطه فوق:
- آنتروپی سیاهچاله است.
- ثابت بولتزمن است.
- سطح مقطع افق رویداد است.
- ثابتی به نام طول پلانک است.
طول پلانک با استفاده از رابطه بهدست میآید. نکته مهم در رابطه آنتروپی سیاهچاله آن است که به جز سطح مقطع افق رویداد، بقیه رابطه از ثابتهای فیزیکی تشکیل شده است. اندازه سطح مقطع به سیاهچاله مورد مطالعه بستگی دارد. تمام ثابتهای استفاده شده در رابطه آنتروپی سیاهچاله را میتوان در ثابتی به نام قرار داد:
بر طبق رابطه بهدست آمده، آنتروپی سیاهچاله به طور مستقیم متناسب با سطح مقطع افق رویداد خواهد بود. در مطالب بالا دیدیم، سطح مقطع افق رویداد نیز به طور مستقیم متناسب با شعاع سیاهچاله است. شعاع سیاهچالهها با استفاده از رابطه زیر بهدست میآید:
همانطور که گفتیم شعاع شوارتزشیلد نام دارد و به ثابت جهانی گرانش، ، سرعت نور، و جرم سیاهچاله، ، بستگی دارد. هر جسمی به جرم برای تبدیل به سیاهچاله باید به اندازهای فشرده شود که شعاع آن برابر شود. به عنوان مثال، ستاره خورشید را در نظر بگیرید. جرم خورشید برابر است. بنابراین، شعاع شوارتزشیلد آن برابر است با:
در نتیجه، برای تبدیل خورشید به سیاهچاله باید تمام جرم آن در ناحیهای به شعاع ۳۰۰۰ متر فشرده شود.
آنتروپی سیاهچاله تنها به سطح مقطع افق رویداد، سطح مقطع تنها به شعاع سیاهچاله و شعاع سیاهچاله تنها به جرم آن بستگی دارد. بنابراین، آنتروپی تنها به جرم سیاهچاله وابسته است. توجه به این نکته مهم است که برای بهدست آوردن رابطه آنتروپی، سیاهچاله را ساکن در نظر گرفتیم.
تا اینجا با دومین قانون از قوانین ترمودینامیک و آنتروپی، به خصوص آنتروپی سیاهچاله، آشنا شدیم. در ادامه، در مورد قوانین ترمودینامیک در سیاهچاله صحبت میکنیم.
قوانین ترمودینامیک سیاهچاله
نسبیت عام در سیاهچاله نمیتواند اتفاقات رخ داده را توجیه کند، بنابراین از نظریههای مختلفی برای توجیه رخدادهای مختلف در سیاهچاله استفاده میشود. سیاهچاله در بیشتر موارد توسط طرحی دایرهای به دور پسزمینه تاریک، شناسایی میشود. به این پسزمینه، سایه سیاهچاله و به طرح دایرهای، کره فوتونی میگوییم. هر جسمی به دام سیاهچاله بیافتد، تا ابد در آنجا خواهد ماند. بنابراین، آنتروپی کیهان کاهش مییابد. بر طبق قانون دوم ترمودینامیک، آنتروپی کیهان همواره افزایش مییابد. چگونه میتوان به این تناقض پاسخ داد؟
سیاهچاله تنها با کمیتهای جرم، تکانه زاویهای و بار کل، مشخصهیابی میشود. بدون داشتن این سه کمیت، هیچ اطلاعاتی در مورد سیاهچاله نخواهیم داشت. در دهه ۷۰ میلادی، فیزیکدانی به نام «استیون هاوکینگ» (Stephen hawking)، اسرارهای زیادی را در مورد سیاهچاله حل کرد. نوری که به سمت سیاهچاله میآید یا توسط آن بلعیده میشود و یا در مداری به دور سیاهچاله قرار میگیرند. بنابراین، مسیرهای پرتوهای نور در افق رویداد باید با یکدیگر موازی باشند یا از مرکز سیاهچاله دور شوند.
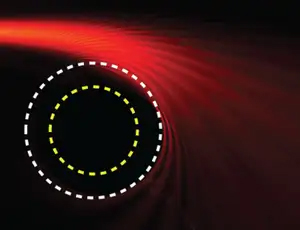
در صورتی که مسیر پرتوهای نور همگرا باشند، داخل سیاهچاله میافتند. بنابراین مساحت افق رویداد همواره ثابت است یا با زمان افزایش مییابد. هر زمان سیاهچاله، ستارهای را میبلعد، مساحت آن افزایش مییابد. در این صورت، شعاع کره فوتونی به دور افق رویداد افزاش خواهد یافت. «یاکوب بکشتاین» (Jacob Bekestein) پدر ترمودینامیک سیاهچاله، رابطه بین افزایش آنتروپی سیاهچاله و افزایش مساحت آن را بهدست آورد. این رابطه در بخش قبل نشان داده شده است. هرچه مساحت سیاهچاله بیشتر باشد، آنتروپی آن نیز بیشتر خواهد بود.

افتادن هر مادهای به داخل سیاهچاله سبب افزایش مساحت سیاهچاله و در نتیجه، افزایش آنتروپی آن خواهد شد. گرچه آنتروپی بیرون سیاهچاله کاهش مییابد، آنتروپی کل کیهان افزایش خواهد یافت. بر طبق قانون دوم ترمودینامیک، آنتروپی تابعی از دما است و با آن رابطه عکس دارد. بنابراین، میتوان نتیجه گرفت سیاهچاله باید دما داشته باشد. تا آن زمان تصور میشد سیاهچاله سردترین جسم در کیهان است. سیاهچالههای کلان جرم، دما دارند. این دما کمتر از دمای پسزمینه مایکروویو کیهانی است. اگر سیاهچاله دما داشته باشد، باید همانند جسم سیاه تشعشع کند. هرچه جرم سیاهچالهای کمتر باشد، دمای آن نیز کمتر خواهد بود. بنابراین، با نرخ کمتری تشعشع میکند.
دمای سیاهچالههای کوچکتر، کمتر است، بنابراین با نرخ بیشتری تشعشع میکنند تا به تعادل برسند. به این تشعشع، تشعشع هاوکینگ گفته میشود. بر طبق مطالعات انجام شده روی سیاهچالهها، مشخصههای سیاهچالهها به چهار قانون تقسیم میشود که به آن قوانین ترمودینامیک سیاهچاله میگوییم.
- قانون صفرم: اگر سیاهچاله ساکن باشد، افق رویداد همواره گرانش سطحی یکسانی خواهد داشت. گرانش سطحی مقدار شتاب گرانشی در استوا و نزدیک سطح جسمی سنگین است.
- قانون اول: تغییر انرژی کل سیاهچاله توسط تغییر در سطح مقطع افق رویداد، تغییر در تکانه زاویهای و تغییر در بار الکتریکی، تعیین میشود. به بیان دیگر، قانون اول، جرم، چرخش و بار سیاهچاله را به آنتروپی آن مربوط میکند. بنابراین، آنتروپی سیاهچاله به سطح مقطع افق رویداد مربوط میشود.
- قانون دوم: این قانون مشابه قانون دوم ترمودینامیک است. بر طبق این قانون، سطح مقطع افق رویداد همواره تابعی افزایشی نسبت به زمان خواهد بود. بنابراین، آنتروپی سیاهچاله نمیتواند کاهش یابد.
- قانون سوم: بر طبق این قانون، آنتروپی سیاهچالههایی با بیشینه بار یا چرخش، کمینه است. این بدان معنا است که تشکیل چنین سیاهچالههایی غیرممکن خواهدبود. این قانون به قانون سوم ترمودینامیک شبیه است.
هاوکینگ در سال ۱۹۷۴ میلادی انتشار تابش گرمایی از سیاهچالهها را کشف کرد. قبل از آن، از سیاهچاله به عنوان آخرین مرحله از مراحل مرگ ستاره یاد میشد. در سالهای اخیر، دانشمندان به این نتیجه رسیدهاند که سیاهچاله سیستم ترمودینامیکی بسیار پیچیدهای است که نهتنها دما، بلکه فشار نیز دارد.
مرگ گرمایی کیهان
سعیدِ ۱۸ ساله به ریاضی بسیار علاقهمند است. به همین دلیل، او تصمیم دارد تحصیلات خود را در رشته ریاضی در دانشگاه ادامه دهد. اما زندگی همیشه براساس پیشبینی ما پیش نمیرود. کدام یک از دو حالت زیر با احتمال بالاتری رخ میدهد؟
- سعید غریق نجات در ساحل است.
- سعید معلم ریاضی در مدرسهای کوچک است و در زمانهای آزاد به عنوان غریق نجات فعالیت میکند.
پاسخ صحیح، گزینه یک است. سعید به عنوان غریق نجات در ساحل فعالیت میکند و هیچ شغل دیگری ندارد. به احتمال زیاد، پاسخ اشتباه را انتخاب کردهاید. در واقع، بیشتر افراد، حتی افرادی که سالها در حوزه آمار فعالیت دارند، پاسخ صحیح را انتخاب نمیکنند. اگر هیچ چیز از سعید، به جز مشکلی که مطرح شد، ندانیم، با اطمینان گزینه دو را انتخاب خواهیم کرد. زیرا از دید ما احتمال رخ دادن گزینه ۲ بیشتر از گزینه یک است. چرا؟ زیرا گزینه دو مشخصتر است. زیرا در این گزینه از دو احتمال صحبت شده است، احتمال آنکه سعید معلم ریاضی شود و احتمال آنکه در وقت آزاد به عنوان غریق نجات فعالیت کند.

سوالاتی همانند سوال بالا در دهه ۸۰ میلادی برای آزمایش سوگیریهای شناختی مطرح شدند. سوالی که ممکن است مطرح شود آن است که چرا طرح این سوال و پاسخ به آن مهم است. زیرا طرح این سوال دیدگاه آماری را مطرح میکند که هر جایی میتواند مناسب باشد. بر طبق این دیدگاه، هرچه پیشبینی دقیقتر باشد، با احتمال کمتری رخ میدهد. اینکه سعید معلم ریاضی و غریق نجات شود، محتملتر به نظر میرسد. زیرا در مقایسه با گزینه یک، مشخصتر است. نکتهای که باید به آن توجه کنیم آن است که رخ دادن گزینه ۲ مستلزم طی کردن راهی مشخص است. بنابراین، با احتمال کمتری رخ میدهد.
به مثال دیگری در این زمینه توجه کنید. کدام یک از گزینههای زیر با احتمال بالاتری رخ میدهد:
- برخورد با صاعقه
- برخورد با صاعقه و تصادف با اتومبیل در یک روز
آیا تاکنون از خود پرسیدهاید چرا بیشتر فرایندهایی که در زندگی ما رخ میدهند، برگشتناپذیر هستند. چرا بیشتر فرایندها تمایل به پیمودن مسیری مشخص دارند؟ چرا شکر در چای حل میشود؟ چرا جفتهای جوراب را باید مرتب کنیم؟ چرا خودبهخود مرتب نمیشوند؟ چرا آب سرد، ناگهان به جوش نمیآید؟ این پرسشها بسیار ساده و پیشپاافتاده به نظر میرسند. درک شهودی که در مورد هر رخداد داریم به ما حتی اجازه پرسیدن چنین پرسشهایی را نمیدهد. دلیل پرسیدن این پرسشها آن است که هیچ نظریه یا قانونی در فیزیک وجود ندارد که عکس فرایندهای پرسیده شده را نقض کند.

قوانینی که بر سرد شدن آبِ گرم حاکم هستند، به هنگام گرم شدن آبِ سرد نیز وجود دارند. بنابراین، کمیت دیگری باید برای ایجاد تعادل وجود داشته باشد. وجود این کمیت به مولکولهای گاز اجازه میدهد تا در اتاق پخش شوند، یا سبب سرد شدن قهوه داغ در هوای سرد میشود. این کمیت، آنتروپی نام دارد. رابطه آنتروپی با احتمال، قویتر از رابطه آن با فیزیک یا شیمی است. در مطالب بالا، با مفهوم آنتروپی به عنوان دومین قانون از قوانین ترمودینامیک آشنا شدیم. این کمیت، نخستین بار در سال ۱۸۶۵ میلادی توسط «رادولف کلازیوس» (Rudolph Clausius) مطرح شد. او از این کمیت برای تعریف دومین قانون از قوانین ترمودینامیک استفاده کرد.

کلمه یونانی برای آنتروپی به بینظمی اشاره نمیکند. در واقع، این کلمه به چرخش همسانگرد اشاره دارد. در مورد تعداد راههای ایجاد تغییر یا انتقال، بدون آنکه جسم متفاوت به نظر برسد، صحبت میکند. به عنوان مثال، میزی نامنظم را در نظر بگیرید. راههای مختلفی برای مرتب کردن میز وجود دارند و به طور مستقیم میتوان آنها را مشخص کرد، زیرا اجسام مختلف روی میز منظم به شکل خاصی چیده شدهاند. اما چیدمان اجسام مختلف روی میز نامنظم از نظم خاصی پیرومی نمیکند. هر جسم میتواند در هر جایی از میز نامنظم باشد. میز میتواند با روشهای زیادی نامنظم شود.
قبل از صحبت در مورد آنتروپی در واقعیت باید به چند نکته کوچک اشاره کنیم. در ابتدای این بخش گفتیم هر چه پیشبینی مشخصتر باشد، احتمال وقوع آن کمتر خواهد بود. از آنجا که چیدمان میز منظم در مقایسه با چیدمان میز نامنظم، مشخصتر است، احتمال داشتن میزی منظم در مقایسه با میزی نامنظم کمتر خواهد بود. به طور حتم در رابطه با این موضوع به درکی شهودی رسیدهاید. اگر میز خود را ابتدای هفته مرتب کنید، احتمال مرتب ماندن آن تا آخر هفته بسیار کم خواهد بود.

اتمها و مولکولهای تشکیلدهنده مواد با اجسام قرار گرفته روی میز بسیار تفاوت دارند. همچنین، مولکولها و اتمها به یکدیگر بسیار شبیه هستند و تشخیص آنها از یکدیگر به راحتیِ تشخیص اجسام روی میز نیست. آنچه درک آنتروپی را بسیار سخت میکند، مقیاس اجسام است. هیچ سرنخی از مقیاس کیهان و تعداد ذرات و اجسام قرار گرفته در آن نداریم. دنیای واقعی بسیار پیچیده است و آنتروپی نقش مهمی در آن ایفا میکند.
انرژی که استفاده میکنیم باید شکل خاصی داشته باشد. میتوان انرژی را ابتدا به شکل غذا فرض کرد. غذا، مولکول است و هر چیزی در کیهان از مولکول تشکیل میشود. اما نمیتوانیم هر چیزی را بخوریم، تنها چیزی قابل خوردن است که مولکولهای تشکیلدهنده آن به شکل خاصی در کنار یکدیگر قرار گرفته باشند. انرژی به تنهایی خیلی مفید نیست. انرژی در سراسر کیهان، از حالت منظم به حالت نامنظم منتقل و سبب از بین رفتن انرژی مفید میشود.
به احتمال زیاد انرژی در آغاز کیهان بسیار منظم بود. سوالی که ممکن است مطرح شود آن است که تبدیل پیوسته حالت منظم انرژی به حالت نامنظم، چه نتیجهای به دنبال خواهد داشت. محتملترین نتیجه، مرگ گرمایی کیهان خواهد بود. هر ثانیه که میگذرد، کیهان یک قدرم به بیشینه آنتروپی نزدیکتر میشود. این بدان معنا نیست که کیهان گرم یا سرد میشود، بلکه به دلیل نبود تفاوت دمایی در کیهان، هیچ فرایند ترمودینامیکی رخ نخواهد داد. در این حالت، هیچ تغییری اتفاق نمیافتد، هیچ اتفاقی رخ نمیدهد. زمان هیچ معنایی نخواهد داشت. این فرایند تدریجی، اجتنابناپذیر و دیدن آن بسیار سخت است. از دید ما، هیچ تفاوتی در کیهان از روزی به روزِ دیگر ایجاد نمیشود.
نویسندهای به نام «استیون پینکر» (Steven Pinker) در کتاب خود به نام «Enlightenment Now» میگوید، قانون دوم ترمودینامیک هدف نهایی زندگی، ذهن و تلاش انسان را تعریف میکند. مرگ گرمایی کیهان هنوز در حد یک نظریه باقی مانده است. مرگ گرمایی کیهان هنگامی رخ میدهد که عمر کیهان، بینهایت باشد.
قانون سوم ترمودینامیک چیست ؟
تا اینجا با قانونهای صفرم، اول و دوم از قوانین ترمودینامیک آشنا شدیم. در این بخش، سومین قانون از قوانین ترمودینامیک را توضیح میدهیم.
در سومین قانون از قوانین ترمودینامیک با مفهوم عجیبی به نام صفر مطلق روبرو میشویم. دما میتواند بسیار بالا یا بسیار پایین باشد. به احتمال زیاد هیچ ایدهای در مورد سردترین دمای ممکن ندارید. دما به صورت اندازهگیری انرژی گرمایی در دسترس، تعریف میشود. انرژی گرمایی برابر مجموع انرژی جنبشی ذرات تشکیلدهنده سیستم است. با کاهش دما، انرژی درونی سیستم و در نتیجه انرژی جنبشی هر ذره کاهش مییابد. اگر دمای سیستم بسیار پایین بیاید، حرکت ذرات آهسته میشود و در نهایت متوقف میشوند. به بیان دیگر، با کاهش دما، انرژی جنبشی ذرات کاهش مییابد.
نبود انرژی جنبشی به معنای نبود دما است. اگر دما را به صورت مجموع انرژی جنبشی ذرات تشکیلدهنده سیستم تعریف کنیم، صفر بودن انرژی جنبشی به معنای صفر بودن دما خواهد بود. به این دما، صفر مطلق گفته میشود و در آن، انرژی جنبشی ذرات تشکیلدهنده سیستم برابر صفر است. در دمای صفر مطلق، هر جسمی، حتی هیدروژن و هلیوم، جامد هستند. قانون سوم ترمودینامیک را میتوان به این صورت نیز بیان کرد، آنتروپی هر ماده کریستالی ایدهآل در صفر مطلق، برابر صفر خواهد بود. هر نقصی در ساختار کریستالی مانع از رسیدن آن به دمای صفر مطلق میشود.
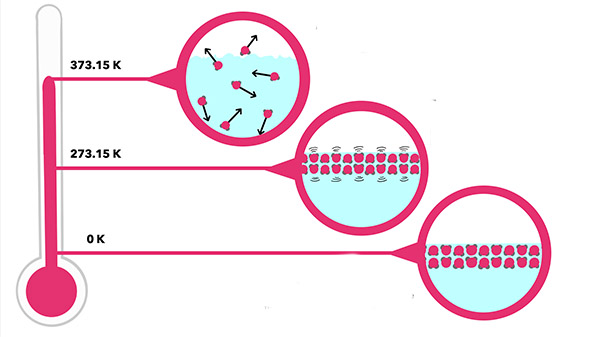
صفر مطلق، قسمتی از مقیاس دمایی کلوین و معادل ۲۷۳- درجه سلسیوس و ۴۵۹- درجه فارنهایت است. اتمهای کریستال در حالت معمولی ارتعاش میکنند و انرژی دارند. هر چه دمای کریستال کمتر شود، انرژی اتمهای کمتر میشود، تا جایی که در صفر مطلق، تمام انرژی خود را از دست میدهند. بر طبق دومین قانون از قوانین ترمودینامیک، گرما از جسمی با دمای بالاتر به جسمی با دمای کمتر منتقل میشود. بنابراین، اینگونه به نظر میرسد که گرما همواره میخواهد وارد سیستمی شود که به صفر مطلق نزدیک میشود.
در مطالب بالا با مفهوم میکروحالت آشنا شدیم. برای درک بهتر آنتروپی، دانستن تعریف میکروحالت ضروری است. به راههای ممکن که اتمها میتوانند در ترازهای انرژی مختلف قرار بگیرند، میکروحالت گفته میشود. به عنوان مثال، اگر سه اتم و سه تراز انرژی داشته باشیم، راههای مختلفی برای چیدن اتمها بین این سه تراز انرژی وجود دارند. در صفر مطلق، تمام اتمها در پایینترین میکروحالت قرار میگیرند و آنتروپی کل برابر صفر میشود. آنتروپی هر سیستم را میتوان با استفاده از رابطه بهدست آورد.
تا اینجا با قوانین ترمودینامیک آشنا شدیم. در ادامه، در مورد کاربرد این قوانین در صنعت و اقتصاد صحبت میکنیم.
قوانین ترمودینامیک در صنعت
روز ۲۶ ماه ژوئن معادل پنجم تیر ماه،روز ترمودینامیک نام دارد. هیچ سیستمی بهتر از سیستم بخار نمیتواند قوانین ترمودینامیک را به خوبی نشان دهد. در این سیستم، قوانین ترمودینامیک به خوبی به صورت عملی نشان داده میشوند. در مطالب بالا در مورد قوانین ترمودینامیک به صورت مفصل صحبت کردیم. در این قسمت، نقش این قوانین را در صنعت توضیح میدهیم.
قانون اول ترمودینامیک در صنعت
بر طبق نخستین قانون از قوانین ترمودینامیک، انرژی کلِ هر سیستم ایزولهای ثابت است. انرژی میتواند از حالتی به حالت دیگر تبدیل شود، اما هرگز نمیتواند تولید شود یا از بین برود. بنابراین، قانون اول ترمودینامیک بیان دیگری از قانون بقای انرژی است و با استفاده از رابطه زیر بیان میشود:
سیستم بخار معمولی را در نظر بگیرید. اگر ۱۰۰٪ انرژی حاصل از سوخت برای به جوش آوردن آب استفاده شود، ۸۰٪ آن به بخار تبدیل میشود. بخار ایجاد شده در شبکه توزیع بخار پخش میشود و به فرایند موردنظر میرسد. گرمای بخار به فرایند موردنظر منتقل و پس از انجام عملیات لازم، به شکل هوای چگال خارج میشود. بنابراین، در هر مرحله شکل انرژی تغییر میکند. در ابتدا انرژی به شکل سوخت فسیلی وارد سیستم بخار میشود. سپس، انرژی حاصل از سوختن سوخت فسیلی به دیگ بخار منتقل و سبب به جوش آمدن آب میشود. سپس به شکل گرما به قسمتهای مختلف فرایند منتقل و در پایان به شکل هوای فشرده از سیستم خارج میشود.

اگر بخواهیم بازده انرژی کل سیستم را بهبود دهیم، باید بدانیم در آن چه اتفاقاتی رخ میدهد. این در حالی است که درک اتفاقاتی که در سیستم واقعی و داخل لولههای فلزی رخ میدهند، بسیار سخت خواهد بود. از قوانین ترمودینامیک برای تحلیل سیستمهای ترمودینامیکی و بهبود بازده آنها استفاده میکنیم. قانون اول ترمودینامیک به ما میگوید تغییرات انرژی درونی سیستم برابر تفاضل انرژی ورودی به سیستم و انرژی خروجی از آن است.
اگر این قانون را برای فرایند تبادل گرمایی استفاده کنیم، مقدار انرژی کسب شده توسط فرایند بهدست میآید. در این حالت، درک بهتری از اتفاقات رخ داده در سیستم بخار داریم. پایستگی و بازده انرژی دو موضوع بسیار مهم در زندگی امروزی هستند. بازده سیستم در صورتی بهبود داده میشود که درکی درستی از عملکرد آن داشته باشیم. آشنایی با قانون اول ترمودینامیک و به کار بردن آن برای سیستم موردمطالعه، کمک شایانی به بهبود بازده انرژی میکند.
سیستم دیگ بخار چگونه کار می کند ؟
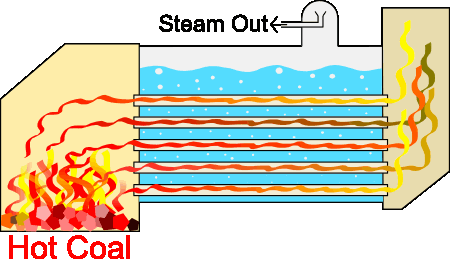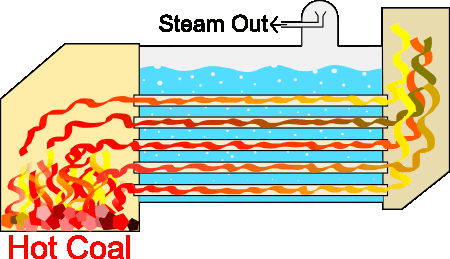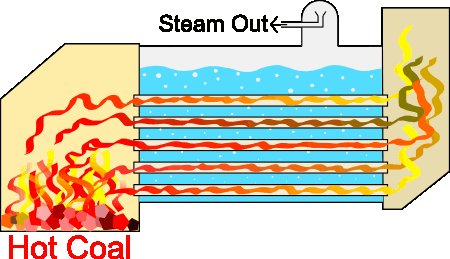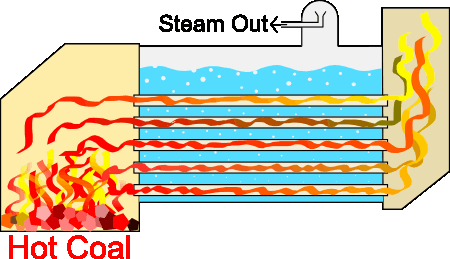
طراحیهای متفاوتی برای سیستمهای بخار وجود دارند، اما اساس کار آنها تقریبا یکسان است. از آنجا که تمام سیستمهای بخار برای هدف یکسانی طراحی شدهاند، قسمتهای پایه آنها شباهت زیادی به یکدیگر دارند. دیگ بخار با استفاده از فرایند احتراق، آب را تا نقطه جوش گرم میکند. احتراق با استفاده از منابع سوختی مختلف انجام میشود. در فرایند احتراق گرما در لولههای غوطهور در آب، تولید میشوند. سیستم دیگ بخار به تولید بخار تحت فشار کمک میکند. دیگهای بخار صنعتی از این فرایند برای حفظ دما یا ایجاد گرمایش، استفاده میکنند.
دیگهای بخار به منظور ایجاد شعله داخل لولهها، واکنشی احتراقی بین هوا و سوخت ایجاد میکنند. این لولهها، گرمای تولید شده را به آب منتقل میکنند. گازهای داغ ایجاد شده توسط مشعل، داخل لولهها سه مرتبه به جلو و عقب حرکت میکنند تا انتقال گرما از سطح لولهها به آب داخل دیگ بخار را به بیشینه مقدار خود برسانند. برای جوشیدن آب در فشار ایجاد شده باید دمای آن به دمایی به نام دمای اشباع برسد. در این حالت، حبابهای بخار تولید خواهند شد. این حبابها به سطح آب میآیند و منفجر میشوند و بخار داخل آنها به فضای بالای آب میرود.
در بخش قبل با کاربرد قوانین ترمودینامیک، به خصوص قانون اول، در صنعت آشنا شدیم. این قوانین نهتنها در صنعت، بلکه در اقتصاد نیز کاربرد دارند. در بخش بعد، در مورد کاربرد قوانین ترمودینامیک در صنعت صحبت میکنیم.
قوانین ترمودینامیک در اقتصاد
ارتباط بین قوانین ترمودینامیک و اقتصاد در نگاه نخست عجیب به نظر میرسد، اما ارتباط بین این دو وسیعتر و عمیقتر از آن است که به نظر میرسد. در این بخش، در مورد این رابطه صحبت میکنیم. در مطالب بالا در مورد انواع سیستمهای ترمودینامیکی صحبت کردیم. سیستمهای ترمودینامیکی به سه دسته سیستم باز، بسته و ایزوله تقسیم میشوند. در سیستمهای باز، ماده و انرژی میتوانند به سیستم وارد و از آن خارج شوند. انسان و دیگر موجودات زنده مثالی از سیستم ترمودینامیکی باز هستند.
در سیستمها ترمودینامیکی بسته، انرژی میتواند به سیستم وارد یا از آن خارج شود، اما ماده نمیتواند. کره زمین، سیستمی بسته است. زمین، مقدار قابل توجهی انرژی از خورشید دریافت می کند و مقداری انرژی نیز به فضا میفرستد. در مقابل، تبادل ماده بین زمین و بقیه منظومهشمسی بسیار کوچک است. در سیستمهای ایزوله، هیچ ماده و انرژی نمیتواند به سیستم وارد یا از آن خارج شود. یافتن مثال برای سیستمهای ایزوله بسیار سخت است. شاید بتوان کیهان را در حالت کلی، سیستمی ایزوله در نظر گرفت. سوال جالبی که ممکن است مطرح شود آن است که اقتصاد کدام یک از سیستمهای بیان شده است.
اقتصاد را میتوان به عنوان سیستمی باز در نظر گرفت. قانون اول ترمودینامیک به ما میگوید انرژی همواره پایسته میماند و تولید یا نابود نمیشود. عبارت مشابهی را نیز میتوان در مورد ماده بیان کرد (قانون پایستگی جرم). در اقتصاد ملی، هر مادهای که از محیط استخراج یا از کشورهای دیگر وارد میکنیم باید:
- به عنوان کالا در انبار ذخیره میشوند.
- از سیستم اقصاد ملی به شکل زباله یا صادرات به کشورهای دیگر خارج میشوند.
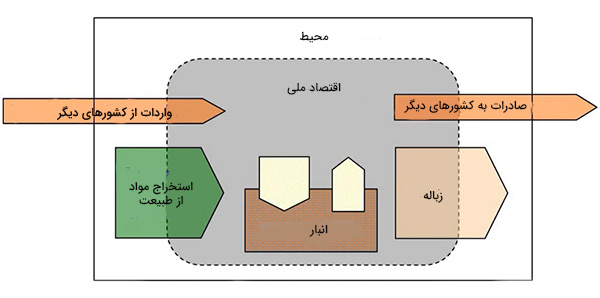
در تصویر بالا، پایستگی ماده را در اقتصاد مشاهده میکنیم. مقدار ماده وارد شده به سیستم اقتصادی برابر مجموع مواد خارج شده از سیستم و مواد جمع شده در آن است. کاربرد قانون اولین ترمودینامیک در اقتصاد، ساده به نظر میرسد، اما قانون دوم کمی چالشبرانگیز است. دومین قانون از قوانین ترمودینامیک میگوید آنتروپی هر سیستم ایزولهای با گذشت زمان افزایش مییابد. در مطالب بالا، آنتروپی را به صورت معیاری برای اندازهگیری میزان بینظمی سیستم تعریف کردیم.
توجه به این نکته مهم است که آنتروپی، تنها در سیستمهای ایزوله افزایش مییابد. در سیستمهای باز یا بسته، آنتروپی ممکن است کاهش یابد. این کاهش در آنتروپی با افزایش آنتروپی در نقطهای دیگر، جبران میشود. به دلیل قانون دوم ترمودینامیک، اتاق شما هیچگاه خودبهخود منظم نمیشود. رابطه بین قانون دوم ترمودینامیک و اقتصاد چیست؟ گرچه مواد میتوانند بازیافت شوند، هیچگاه نمیتوان آنها را به صورت ۱۰۰٪ بازیافت کرد. بازیافت ۱۰۰٪ نیاز به انرژی بسیار زیادی دارد.
گرچه میتوان مواد را تا درصد زیادی بازیافت کرد، انرژی نمیتواند بازیافت شود. کمیت انرژی در هر فرایندی پایسته است، اما دسترسی به انرژی برای انجام کار کاهش مییابد. در تمام فرایندهای فیزیکی، مواد و انرژی با آنتروپی کم به زبالههایی با آنتروپی بالا تبدیل میشوند. همچنین، ساختار هر کالای فیزیکی با گذشت زمان فاسد میشود. برای مقابله با فاسد شدن کالا باید انرژی مصرف شود. کاهش آنتروپی در نقطهای خاص به معنای افزایش آنتروپی در نقطهای دیگر است.
سوالی که ممکن است مطرح شود آن است که آیا زندگی روی زمین، قانون دوم ترمودینامیک را نقض میکند. چگونه نظم و پیچیدگی در زیستکره، قانون دوم ترمودینامیک مبنی بر افزایش آنتروپی را نقض نمیکند؟ پاسخ به این پرسش به مرزهای سیستمهای ترمودینامیکی مربوط میشود. زمین، سیستمی بسته است و ایزوله نیست. اقتصاد سیستمی است برای پاسخگویی به نیازهای انسان که مواد خام با آنتروپی کم را به زبالههایی با آنتروپی بالا تبدیل میکند. نظم سیستمی اقتصادی تنها زمانی میتواند نگه داشته شود که جریانی از مواد و انرژی با آنتروپی کم وجود داشته باشد. تمام تولید اقتصادی بر پایه منابع ایجاد شده توسط طبیعت استوار است.
جمعبندی
در این مطلب، در مورد قوانین ترمودینامیک صحبت کردیم. از این قوانین برای مطالعه سیستمهای ترمودینامیکی در حالت تعادل ترمودینامیکی استفاده میکنیم. قوانین ترمودینامیک به صورت خلاصه به شکل زیر نوشته میشوند:
- قانون صفرم ترمودینامیک: بر طبق قانون صفرم از قوانین ترمودینامیک، اگر سیستم A در تعادل ترمودینامیکی با سیستم C و سیستم B نیز در تعادل ترمودینامیکی با سیستم C باشد، سیستمهای A و B نیز در تعادل ترمودینامیکی با یکدیگر قرار دارند.
- قانون اول ترمودینامیک: این قانون صورت دیگری از اصل پایستگی انرژی است. انرژی میتواند از طریق برهمکنش با گرما، کار و انرژی درونی، از شکلی به شکل دیگر تبدیل شود.
- قانون دوم ترمودینامیک: بر طبق این قانون، آنتروپی کیهان، به عنوان سیستمی ایزوله، همواره با زمان افزایش مییابد. از اینرو، تغییرات آنتروپی در کیهان و در هیچ سیستم بستهای، هرگز نمیتوانند منفی باشد.
- قانون سوم ترمودینامیک: بر طبق این قانون، اگر ساختار کریستالی را با خلوص ۱۰۰٪ در دمای صفر کلوین در نظر بگیریم، آنتروپی آن برابر صفر خواهد بود.













سلام
در مثالی با عنوان پرتاب سنگ به بالا، چرا اگر از مقاومت هوا صرفنظر کنیم، سرعت برخورد با سرعت اولیه متفاوت است؟ در حالی که هر دو حالت رفت و برگشت از مقاومت هوا صرفنظر شده و شرایط یکسان است..
با سلام خدمت شما؛
در متن بیان شده که سرعت پرتاب سنگ با سرعت برخورد آن به زمین برابر است، اما سرعت پرتاب با سرعت در بالاترین ارتفاع، متفاوت است. پرتاب سنگ به سمت بالا یک نوع حرکت پرتابی است. حرکت پرتابی با صرفنظر کردن از مقاومت هوا یا نیروهایی مانند نیروی باد و … و با در نظر گرفتن اینکه تنها نیروی وارد بر جسم نیروی وزن آن است، همواره یک حرکت متقارن است، به این معنا که سرعت در هر ارتفاع مشخصی از سطح زمین با نقطه متناظر آن در سمت دیگر منحنی حرکت پرتابی برابر است. در این زمینه میتوانید مطلب «حرکت پرتابی — به زبان ساده» از مجله فرادرس را مطالعه کنید.
از همراهی شما با مجله فرادرس سپاسگزاریم.