الگوریتم BFS چیست؟ – به زبان ساده + مثال
یکی از موضوعات مهم در مباحث طراحی الگوریتم و برنامه نویسی، روشهای جستجو در «ساختمان دادههای» (Data Structures) مختلف است. به عبارتی، از الگوریتمهای جستجو به منظور بازیابی مقادیر خاصی از اطلاعات ذخیره شده در ساختار دادههای مختلف استفاده میشود. الگوریتم «جستجوی اول سطح» (Breadth First Search | BFS) به عنوان یکی از الگوریتمهای جستجوی رایج برای «گراف» (Graph) و «درخت» (Tree) محسوب میشود. در این مطلب از مجله فرادرس قصد داریم به این پرسش پاسخ دهیم که ویژگیها و مزایا و معایب الگوریتم BFS چیست و با ارائه یک مثال ساده، به توضیح مرحله به مرحله این الگوریتم برای پیدا کردن پاسخ مسئله میپردازیم.
- یاد میگیرید تفاوتهای اجرایی BFS در گراف و درخت را تشخیص دهید.
- درک میکنید چگونه با استفاده از صف روند BFS را اجرا کنید.
- خواهید توانست کوتاهترین مسیر را در گرافهای بدون وزن بیابید.
- میآموزید وضعیت گرهها را برای جلوگیری از گردش بیهوده مدیریت کنید.
- یاد میگیرید ساختارهای لازم برای پیادهسازی BFS را آماده کنید.
- تحلیل میکنید که افزایش ابعاد داده چگونه بر عملکرد BFS اثر میگذارد.


الگوریتم های پیمایش ساختار داده ها
الگوریتمهای پیمایش، روشی برای جستجوی یک گره در ساختمان دادههای درخت و گراف به حساب میآیند. درخت و گراف به عنوان ۲ ساختار داده در طراحی الگوریتم و برنامه نویسی محسوب میشوند که از آنها میتوان برای نمایش و نگهداری دادهها به نحوی استفاده کرد که ارتباطی بین آنها وجود داشته باشد. این نوع ارتباط در ساختار داده درخت میتواند به صورت سلسلهمراتبی و بدون وجود حلقه باشد و در گراف میتوان ارتباطی را بین دادهها ایجاد کرد که باعث شکلگیری حلقه در گراف شود.
به منظور یافتن مقداری خاص در این ۲ نوع ساختار داده، میتوان از ۲ روال جستجو استفاده کرد:
- روش «جستجوی اول سطح» (Breadth-First Search) یا همان الگوریتم BFS
- روش «جستجوی اول عمق» (Depth-First Search) یا الگوریتم DFS
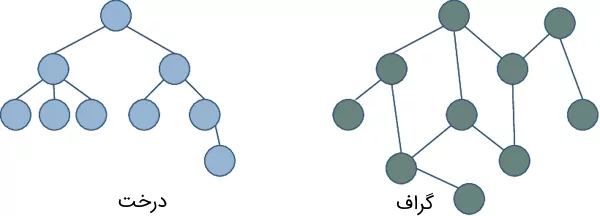
در مطلب حاضر، قصد داریم به روش جستجوی اول سطح بپردازیم و با مثال کاربردی مراحل آن را توضیح دهیم.
الگوریتم BFS چیست ؟
الگوریتم BFS برای جستجوی مقداری خاص در یک درخت یا گراف استفاده میشود. روال جستجوی الگوریتم BFS از گره ریشه درخت یا گراف آغاز میشود. در هر سطح از درخت یا گراف، تمامی گرهها مورد بررسی قرار میگیرند و سپس روند جستجو در سطح بعدی این ساختار دادهها ادامه پیدا میکند. با کمک این الگوریتم میتوان بدون گیر افتادن در یک حلقه بیپایان، هر گره را بررسی کرد.
الگوریتم جستجوی اول سطح از ساختار داده «صف» (Queue) برای پیمایش گراف یا درخت استفاده میکند. یکی از اصول ساختار داده صف، اصل «اولین ورودی - اولین خروجی» (First In - First Out | FIFO) است. الگوریتم BFS با استفاده از چنین اصلی، در هر گامی که گره جدیدی را در گراف یا درخت ملاحظه میکند، گرههای مجاور (گرههای فرزند) آن را در صف قرار میدهد و سپس گرههای موجود در صف را با اصل FIFO برای یافتن پاسخ، بررسی میکند. به منظور درک بهتر عملکرد این الگوریتم، در بخشهای بعدی این مطلب، مثالی کاربردی ارائه کردهایم.
کاربرد الگوریتم جستجوی اول سطح
الگوریتم BFS به عنوان یکی از الگوریتمهای ساده جستجو محسوب میشود و میتوان به سادگی آن را با استفاده از زبان برنامه نویسی پیادهسازی کرد، از این الگوریتم در مسائل مختلف مهمی استفاده میشود که در ادامه به برخی از آنها اشاره شده است:
- کاربرد الگوریتم BFS در پیدا کردن کوتاهترین مسیر پاسخ در گراف غیر وزندار: از آنجایی که الگوریتم BFS سطر به سطر سطح یک درخت را پیمایش میکند، این تضمین وجود دارد که کوتاهترین مسیر برای پیدا کردن گره مورد نظر طی شده است.
- کاربرد الگوریتم جستجوی اول سطح در شبکههای نظیر به نظیر «Peer To Peer Networks»: در چنین شبکههایی مانند شبکه BitTorrent از این الگوریتم به منظور پیدا کردن گرههای همسایه استفاده میشود.
- استفاده از الگوریتم BFS در موتورهای جستجو: «خزشگر» (Crawler) وب از این الگوریتم برای استخراج اطلاعات از صفحات اینترنت استفاده میکند. خزشگرها با کمک این روش، از یک صفحه اینترنتی، کار استخراج اطلاعات را شروع میکنند و با استفاده از لینکهای موجود در صفحه اینترنت، روند جستجوی خود را در صفحات لینک داده شده، ادامه میدهند.
- استفاده از الگوریتم جستجوی اول سطح در شبکههای اجتماعی: یافتن افراد مختلف در شبکههای اجتماعی بر اساس این الگوریتم انجام میشود. برای مثال، این الگوریتم افرادی را که با دوستان شما لینک هستند، به شما پیشنهاد میدهند تا اگر آنها را میشناسید، با آنها ارتباط برقرار کنید.
- کاربرد الگوریتم BFS در شبکه: از این الگوریتم میتوان برای انتشار بسته در طول یک شبکه استفاده کرد تا بسته ارسالی به تمامی گرهها برسد.
- تشخیص وجود حلقه در گرافهای جهتدار و غیر جهتدار با استفاده از الگوریتم جستجوی اول سطح
- بررسی تمامی گرهها: با استفاده از الگوریتم جستجوی اول سطح میتوان تمام گرههایی را درون گراف یا درخت پیدا کرد که از گره آغازین میتوان به آنها دسترسی داشت.
تفاوت پیمایش الگوریتم BFS در گراف و درخت چیست ؟
همانطور که گفتیم، از الگوریتم جستجوی اول سطح به منظور پیمایش درخت یا گراف برای یافتن مقداری خاص استفاده میشود. روال پیمایش الگوریتم BFS در گراف، مشابه با روال جستجوی این الگوریتم در ساختار داده درخت است. تنها نکتهای که باید به آن توجه کنیم، این است که گراف میتواند شامل حلقه باشد. به همین خاطر، در روال جستجو ممکن است با یک گره بیش از یک بار برخورد کنیم.
به منظور جلوگیری از بازدید یک گره بیش از یک بار، میتوان دو دسته مجزا برای راسهای گراف در نظر بگیریم:
- راسهای دیده شده
- راسهای دیده نشده
برای استفاده از الگوریتم جستجوی اول سطح در پیمایش درخت، چنین شرطی لحاظ نمیشود، زیرا ساختار درخت به نحوی است که حلقه در آن ایجاد نمیشود. در ادامه مطلب، به مراحل الگوریتم BFS میپردازیم و مثال واضحی برای آن ارائه خواهیم کرد.
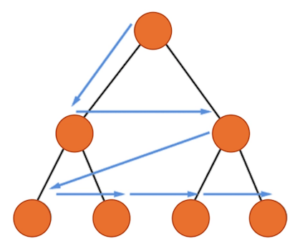
مراحل الگوریتم جستجوی اول سطح چیست ؟
مراحل پیمایش گراف یا درخت را با استفاده از الگوریتم BFS میتوان در چندین مرحله خلاصه کرد. در ادامه، به توضیح این مراحل میپردازیم:
- گام اول: گرافی را تعریف کنید که قصد پیمایش آن را با استفاده از الگوریتم BFS دارید.
- گام دوم: راس نخست گراف را انتخاب کنید. پیمایش گراف، از این راس آغاز میشود.
- گام سوم: میتوان از ساختار دادههای «آرایه» (Array) و صف برای پیمایش گراف استفاده کرد. آرایه تعریف شده، برای نگهداری راسهایی از گراف هستند که با پیمایش گراف، ملاحظه شدهاند.
- گام چهارم: راس اول را به آرایه اضافه کنید. سپس، راسهای مجاور راس نخست را به ساختار داده صف اضافه کنید.
- گام پنجم: از روش «اولین ورودی - اولین خروجی» (First In - First Out | FIFO) برای حذف اولین آیتم موجود در صف استفاده کنید. آیتم خارج شده از صف را درون آرایه قرار دهید و سپس راسهای مجاور آیتم حذف شده را به صف اضافه کنید.
- گام ششم: گام پنجم را آنقدر تکرار کنید تا راسی از گراف باقی نماند.
مثال کاربردی از الگوریتم BFS
در این بخش قصد داریم مثالی ساده برای درک بهتر از عملکر الگوریتم جستجوی BFS ارائه کنیم. بدین منظور، در مرحله اول، گرافی را برای پیمایش تعیین میکنیم که در ادامه آن را ملاحظه میکنید.
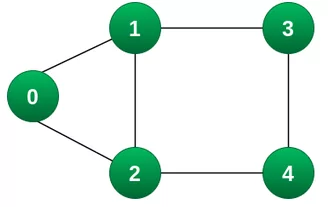
در مرحله دوم، ۲ ساختار داده خالی آرایه و صف ایجاد میکنیم.
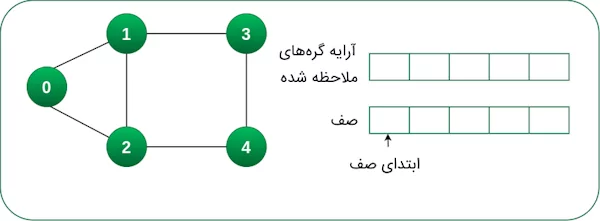
در مرحله سوم، گره اول گراف را درون صف قرار میدهیم و این گره را به عنوان گره ملاحظه شده درون آرایه ذخیره میکنیم.
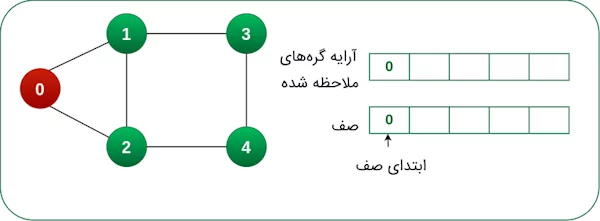
گره ملاحظه شده را از ابتدای صف حذف میکنیم و گرههای مجاور گره حذف شده از صف را درون صف و آرایه قرار میدهیم.
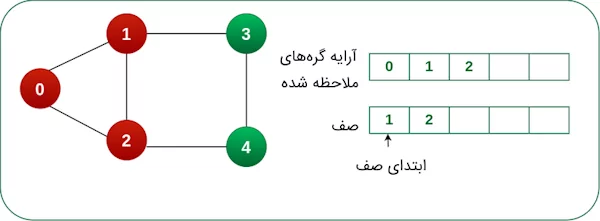
گره ۱ را از ابتدای صف حذف و گره مجاور آن را به صف و آرایه اضافه میکنیم.
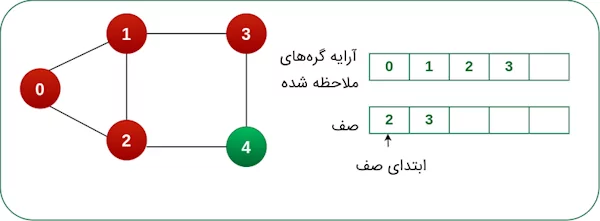
سپس، گره ۲ را از ابتدای صف حذف کرده و گره مجاور آن را به صف و آرایه اضافه میکنیم.
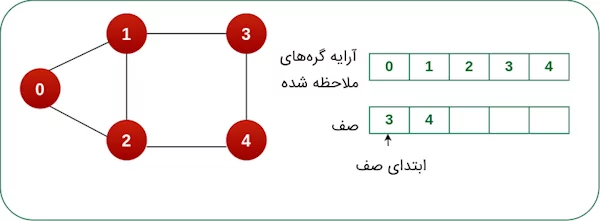
گره ۳ را از صف حذف میکنیم و اگر گره ۳ دارای گره مجاوری باشد که از قبل، آن گره ملاحظه نشده باشد، آن را به صف و آرایه اضافه میکنیم. از آنجایی که گره ۴ به عنوان گره مجاور گره ۳ است و در مراحل قبل، گره ۴ به آرایه اضافه شده بود، مجدداً آن را به آرایه اضافه نمیکنیم. بدینترتیب، گره بعدی موجود در صف را حذف میکنیم.
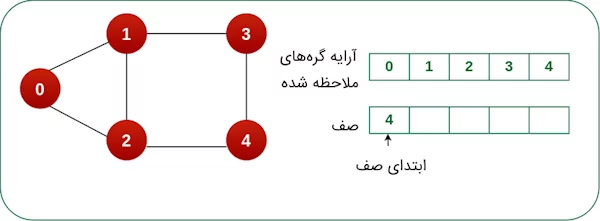
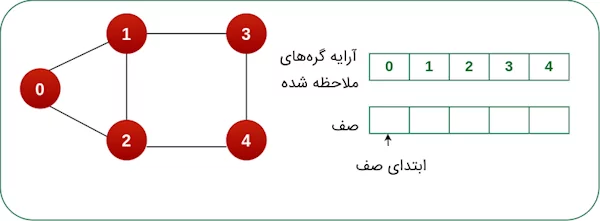
پس از حذف گره ۴ از صف، بررسی میکنیم آیا گره مجاور جدیدی برای گره ۴ وجود دارد؟ همانطور که در تصویر زیر ملاحظه میکنید، گره مجاور جدیدی برای گره ۴ موجود نیست و تمامی گرههای گراف با استفاده از الگوریتم BFS پیمایش شدند. در صورتی که گرهای از گراف باقی نمانده باشد، صف مقدارش خالی میشود و در این حالت، کار پیمایش الگوریتم BFS به اتمام میرسد.
پیچیدگی زمانی و پیچیدگی فضایی الگوریتم جستجوی BFS چیست؟
پیچیدگی زمانی الگوریتم جستجوی BFS را میتوان به صورت O(|V|+|E|) نشان داد، زیرا این الگوریتم در بدترین شرایط تمامی گرههای درخت یا گراف را برای یافتن پاسخ مسئله، جستجو میکند. |V| تعداد گرهها و |E| تعداد یالهای گراف یا درخت را مشخص میکنند. پیچیدگی فضایی الگوریتم جستجوی اول سطح نیز برابر با O(|V|) یا O(b^d) است که |V| تعداد گرههای گراف یا درخت را تعیین میکند و b و d به ترتیب تعداد فرزندان هر گره و عمق درخت را نشان میدهند.
مزایای الگوریتم جستجوی اول سطح
الگوریتم جستجوی BFS، الگوریتم سادهای است که به دلیل داشتن مزیتهای مهم، از آن در حل مسائل مهمی استفاده میشود. در ادامه، به برخی از مهمترین مزیتهای این الگوریتم اشاره شده است:
- در این روش جستجو، چنانچه تنها یک راهحل برای یافتن گره مورد نظر وجود داشته باشد، در نهایت آن گره توسط الگوریتم BFS پیدا خواهد شد.
- اگر بیش از یک راه برای رسیدن به پاسخ مسئله وجود داشته باشد، الگوریتم جستجوی اول سطح، کوتاهترین راه را پیدا میکند.
- چنانچه ساختار دادههای درخت یا گراف دارای گرههای زیادی نباشند، در هنگام استفاده از الگوریتم BFS به حجم زیادی از حافظه نیازی نداریم.
- پیادهسازی این الگوریتم با استفاده از زبانهای برنامه نویسی، ساده است.
معایب الگوریتم BFS چیست ؟
یکی از مهمترین معایب الگوریتم جستجوی اول سطح یا همان BFS این است که به حجمی از حافظه برای ذخیرهسازی گرههای گراف یا درخت احتیاج دارد. میزان حافظه مصرفی نیز به تعداد گرههای ذخیره شده بستگی دارد. میتوان گفت میزان پیچیدگی فضای مورد نیاز این الگوریتم، برابر با b به توان d است.
حرف b تعداد فرزندان هر گره را مشخص میکند و حرف d برابر با عمیق درخت است. بنابراین، چنانچه تعداد گرههای گراف یا درخت زیاد باشند، نمیتوان این روش را بر روی کامپیوترهای معمولی با میزان حافظه پایین اجرا کرد.
پیاده سازی الگوریتم جستجوی اول سطح
در این بخش، نحوه پیادهسازی الگوریتم BFS را برای مثال گرافی ملاحظه میکنید که در بخش قبل ارائه کردیم. قطعه کدهای ارائه شده به ۶ زبان برنامه نویسی C ،C++ ،C# ،جاوا، جاوا اسکریپت و پایتون هستند که خروجی تمامی این قطعه کدها، یکسان است.
پیاده سازی الگوریتم BFS با زبان برنامه نویسی C
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی C ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 پیاده سازی الگوریتم BFS با زبان برنامه نویسی C++
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی C++ ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 پیاده سازی الگوریتم جستجوی اول سطح با سی شارپ
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی C# ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 پیاده سازی الگوریتم جستجوی اول سطح با جاوا
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی Java ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 پیاده سازی الگوریتم جستجوی اول سطح با جاوا اسکریپت
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی JavaScript ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 پیاده سازی الگوریتم جستجوی اول سطح با پایتون
در قطعه کد زیر، نحوه پیادهسازی الگوریتم جستجوی اول سطح را با زبان برنامه نویسی پایتون ملاحظه میکنید.
خروجی قطعه کد بالا را در ادامه ملاحظه میکنید:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 جمعبندی
یکی از اهداف ذخیرهسازی دادهها در ساختمان دادههای مختلف این است که بتوانیم در صورت نیاز، اطلاعاتی را از آنها بازیابی کنیم. الگوریتمهای جستجو بدین منظور استفاده میشوند و از روشهای جستجوی مختلفی میتوان برای استخراج اطلاعات از ساختار دادهها استفاده کرد.
از الگوریتم BFS میتوان به عنوان یکی از پرکاربردترین الگوریتمهای جستجو یاد کرد که کاربردهای متنوعی در مسائل مختلف دارد. در این مطلب از مجله فرادرس سعی داشتیم به این پرسش پاسخ دهیم که الگوریتم BFS چیست و چه ویژگیهایی دارد. سپس، با ارائه یک مثال کاربردی، مراحل کار این الگوریتم را شرح دادیم تا درک آن برای خوانندگان ساده باشد.













توضیحات کاملی بود، لذت بردم