تولید مجموعه دادههایی با محتوای یکسان و نمودارهای متفاوت به کمک الگوریتم تبرید شبیهسازیشده

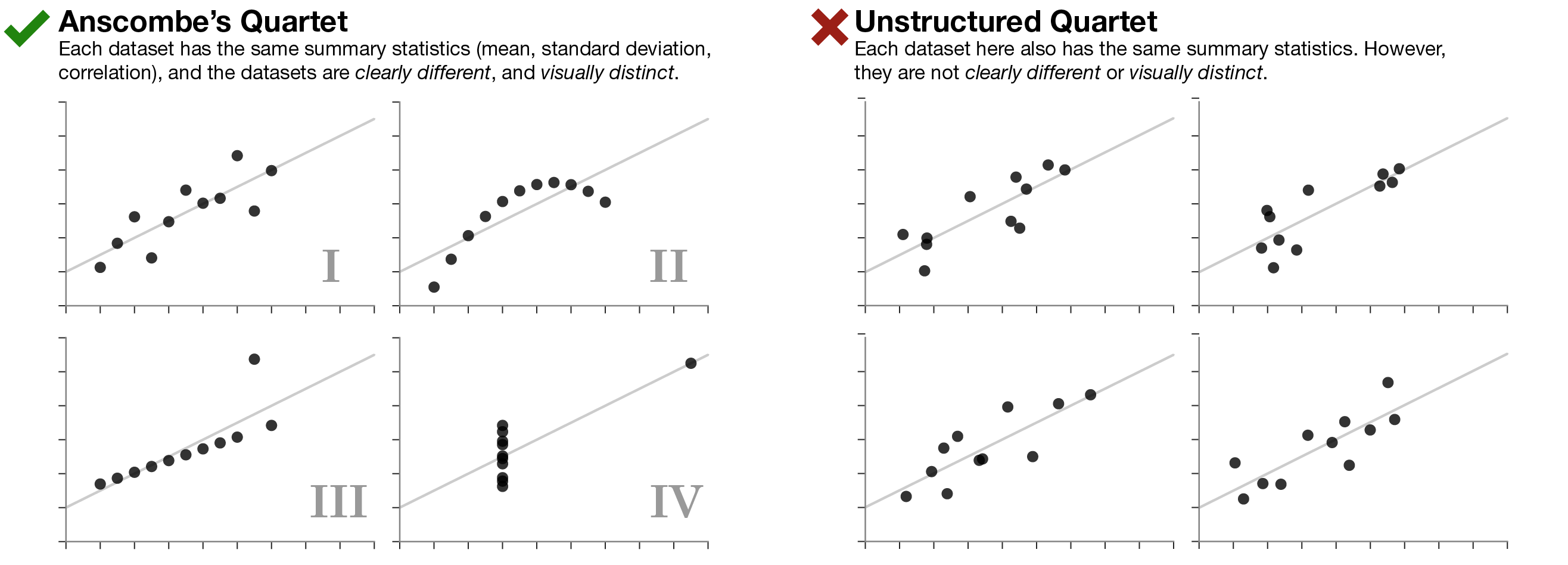
بیان اهمیت بصری سازی دادهها کاری دشوار است. برخی افراد بر این باورند که نمودارها تنها تصاویری زیبا هستند و همه اطلاعات مهم را میتوان از طریق تحلیل آماری استنباط کرد. ابزار کارآمدی که غالباً برای نمایش اهمیت بصری سازی دادهها استفاده میشود، نمودار چهار بخشی آنسکام (Anscome's Quartet) است که توسط اف. جی. آنسکام در سال 1973 ارائه شده است.
این نمودار چهار بخشی مجموعهای از چهار دیتاست است که هر یک آمار توصیفی (میانگین، انحراف معیار، و همبستگی) یکسانی دارند. با این حال پس از بصری سازی (ترسیم) دادهها مشخص میشود که مجموعه دادهها به طرز متفاوتی نمایش مییابند.
کارآمدی نمودار چهار بخشی آنسکام به این دلیل نیست که صرفاً چهار مجموعه داده متفاوت با آمار یکسان دارد، بلکه دلیل آن این است که مجموعه دادههای کاملاً متفاوت و از نظر بصری متمایز، مشخصات آماری یکسانی ارائه میکنند. برخلاف این وضعیت، «نمودار چهار بخشی ساخت نیافته» در سمت راست شکل زیر مشخصات آماری یکسانی با نمودار چهار بخشی آنسکام دارد؛ اما ساختار تشکیل دهنده مجموعه دادهها یکسان نیست و این نمودار چهار بخشی، میزان اهمیت بصری سازی دادهها را به خوبی نشان نمیدهد.
با این که این نمودارهای چهار بخشی آنسکام برای نمایش اهمیت بصری سازی دادهها بسیار رایج و کارآمد هستند و بیش از 45 سال از معرفی آنها میگذرد؛ اما مشخص نیست که آنسکام چگونه به این مجموعه دادهها دست یافته است. بنابراین ما اقدام به توسعه چارچوبی کردیم تا به چنین مجموعه دادههایی دست پیدا کنیم که در زمینه پارهای مشخصات آماری، مقادیر یکسانی داشته باشند و در عین حال نمودارهای متمایزی را تولید کنند.
اخیراً آلبرتو کایرو یک مجموعه داده Datasaurus ایجاد کرده است تا افراد را قانع کند که «هرگز صرفاً به آمار توصیفی اتکا نکنند؛ و همواره در جهت بصری سازی دادهها اقدام نمایند.» در این مجموعه داده گرچه آمار توصیفی نرمالی مشاهده میشود؛ اما ترسیم دادهها تصویری از یک دایناسور را نمایش میدهد. ما با الهام گرفتن از نمودار چهار بخشی آنسکام و Datasaurus، مجموعه داده Datasaurus Dozen را ارائه کردهایم (دانلود فایل CSV.) .

این 13 مجموعه داده (Datasaurus به همراه 12 مجموعه داده دیگر) هر یک آمار توصیفی (میانگین، انحراف معیار و همبستگی پیرسون) یکسانی تا دو رقم اعشار دارند و در عین حال در هنگام ترسیم، نمودارهای متفاوتی تولید میکنند. این تحقیق روشی که برای تولید این مجموعه دادهها و انواع مشابه آن استفاده شده است را توضیح میدهد.
روش
بینش اصلی الهامبخش این رویکرد آن است که گرچه تولید مجموعه دادهای که مشخصات آماری مشخص داشته باشد، کار دشواری است؛ اما انتخاب یک مجموعه داده و اصلاح اندک آن برای رسیدن به آن مشخصات آسان است. بنابراین ما نقاطی تصادفی انتخاب کردیم، آنها را اندکی تغییر دادیم و سپس بررسی کردیم که آیا مشخصات آماری از محدوده مورد نظر خارج شده است یا نه. در این مورد خاص میبایست مطمئن میشدیم که میانگین، انحراف معیار و همبستگی تا دو رقم اعشار در محدوده مشخص باقی میماند)
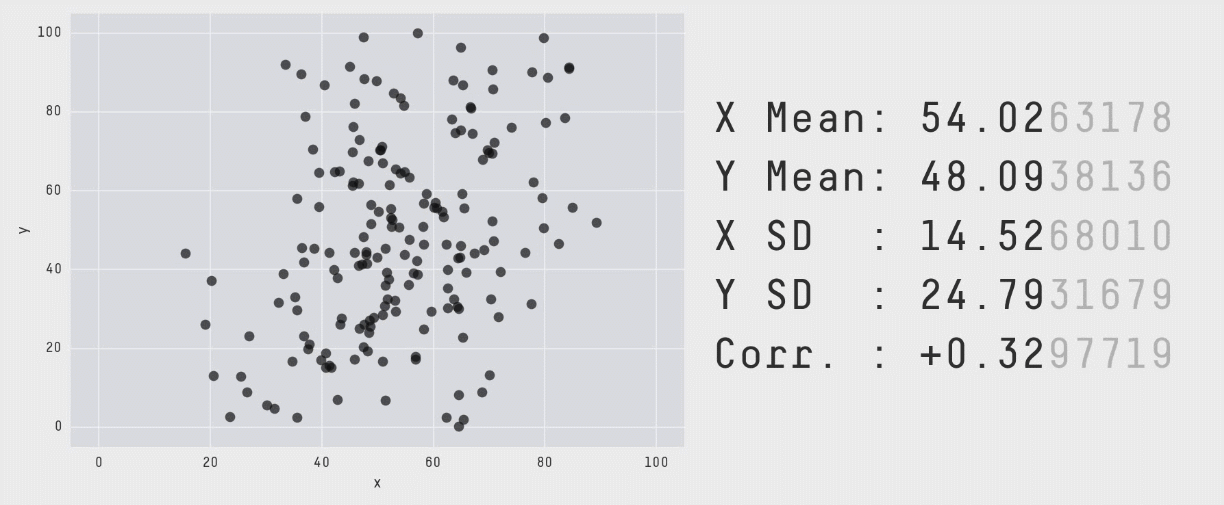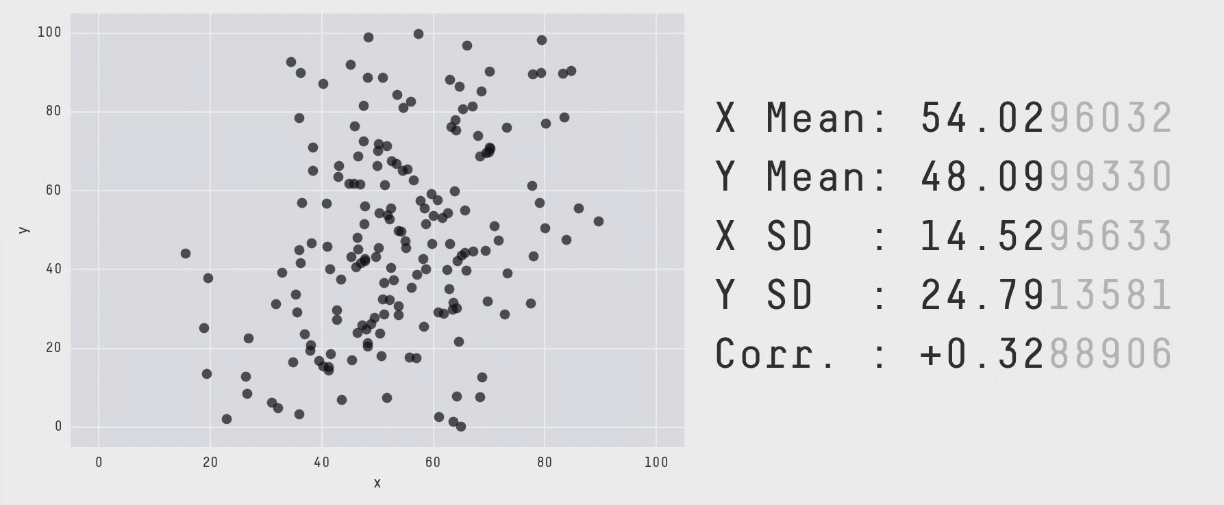
با تکرار این فرایند «آشفتگی» به دفعات کافی، نتایج به صورت مجموعه دادهای کاملاً متفاوت ظاهر میشوند. با این حال همانطور که قبلاً اشاره کردیم برای این که این مجموعه دادهها ابزار کارآمدی برای نمایش اهمیت بصری سازی دادهها باشند، باید از نظر بصری متمایز و کاملاً متفاوت باشند. این وضعیت با سوق دادن حرکات نقاط تصادفی به سمت یک شکل خاص حاصل شده است. در انیمیشن زیر یک فرایند دارای 200،000 تکرار آشفتگی را نشان میدهیم که به سمت تشکیل یک دایره حرکت میکند:
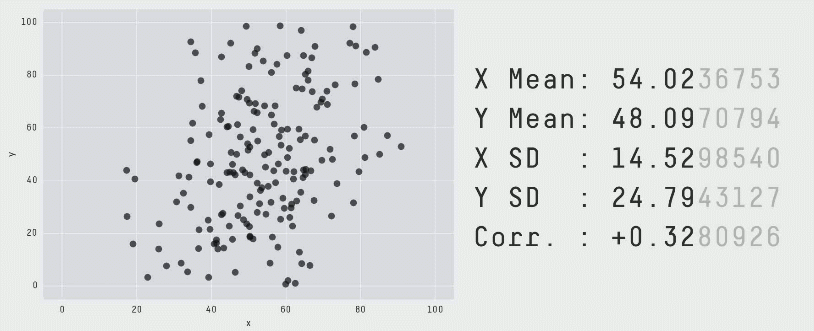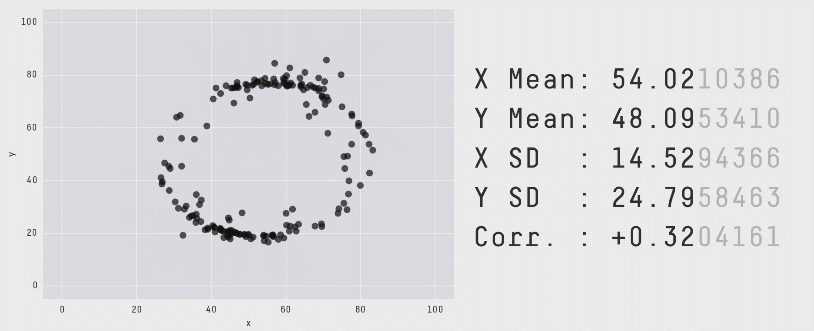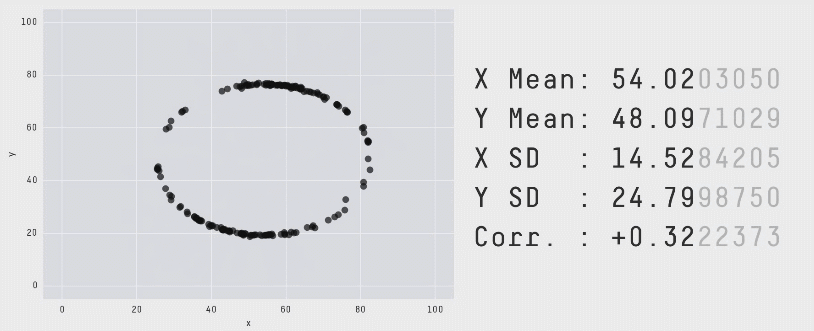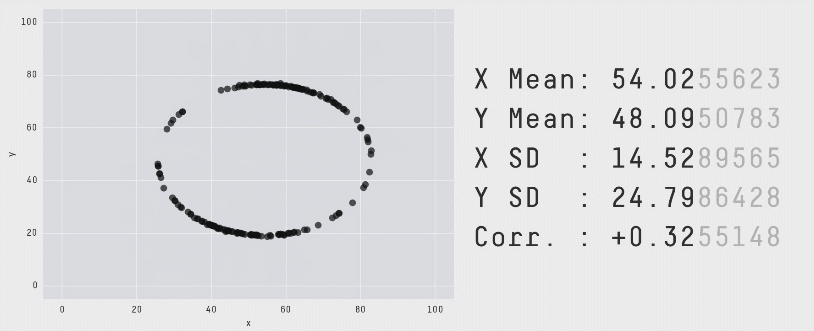
برای این که نقاط به سمت یک تشکیل یک شکل خاص حرکت کنند، میبایست پس از هر مرحله آشفتگی تصادفی بررسیهایی انجام دهیم. علاوه بر بررسی این که مشخصات آماری همچنان معتبر هستند، همچنین باید ببینیم که آیا نقاط به سمت تشکیل آن شکل خاص نزدیک شدهاند یا نه. اگر هر دو شرایط برقرار باشند، موقعیت جدید پذیرفته میشود و به تکرار بعدی میرویم. برای کاهش احتمال این که در یک وضعیت بهینه موضعی قرار بگیریم و راهحلهای بهینه کلی به شکل مورد نظر نزدیکتر باشند از تکنیک تبرید شبیهسازیشده استفاده کردیم که با پذیرش برخی راهحلها که در آنها نقاط در تکرارهای اولیه از شکل مطلوب فاصله میگیرند استفاده میشود. بدین ترتیب فراوانی چنین پذیرشهایی در طی زمان کاهش مییابد.
برای تولید Datasaurus Dozen 12 شکل ایجاد کردیم که نقطهها را به سمت یکدیگر هدایت میکرد. هر یک از نمودارهای حاصل آمار توصیفی یکسانی با Datasaurus داشتند و در واقع همه فریمهای میانی نیز چنین بودند. فرایند تبدیل Datasaurus به هر یک از این شکلها را در ادامه میتوانید مشاهده کنید. البته این تکنیک محدود به این شکلها است و هر مجموعهای از قطعات خط را میتوان به عنوان یک هدف در نظر گرفت.
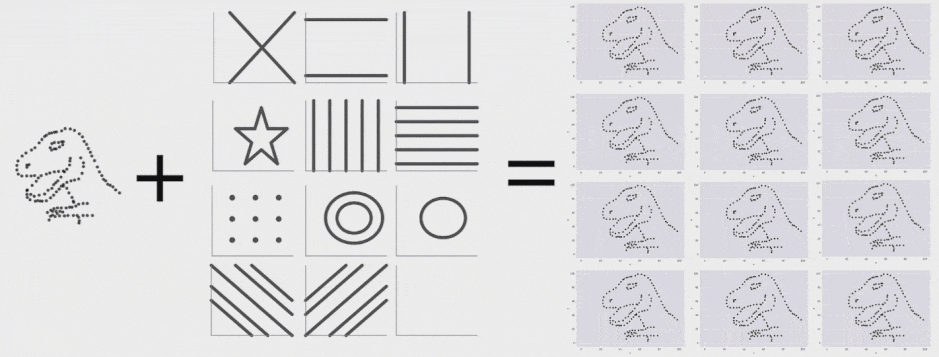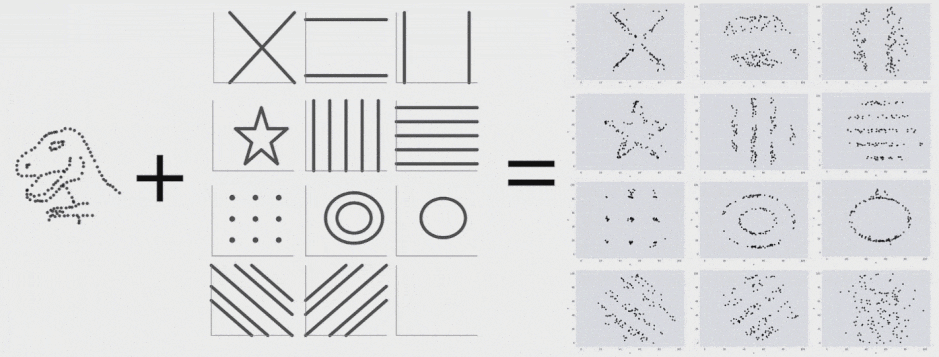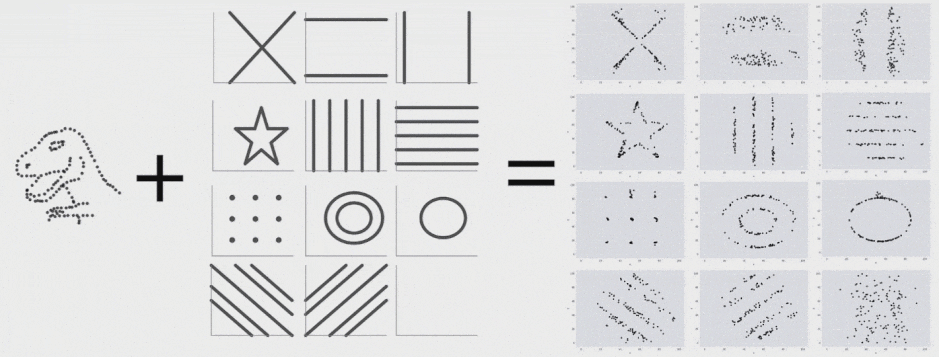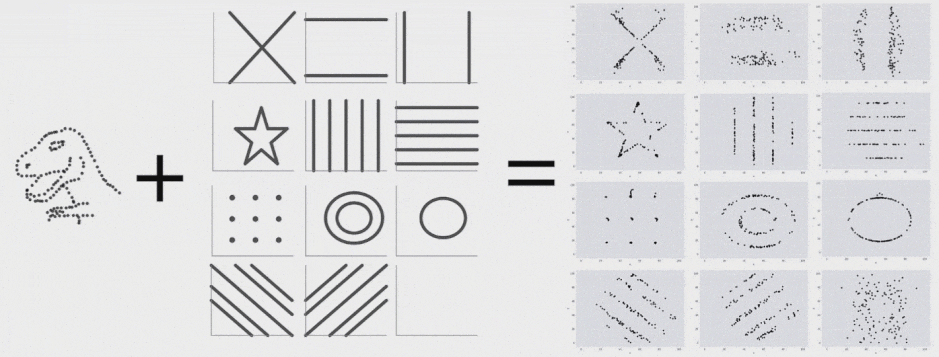
با اجرای متوالی تکرارها بر روی مجموعه دادهها میتوانیم ببینیم که نقاط دادهای از یک شکل به شکل دیگر تغییر مییابند و در عین حال مقادیر آمار توصیفی تا دو رقم اعشار در طی دوره کامل فرایند ثابت میمانند.
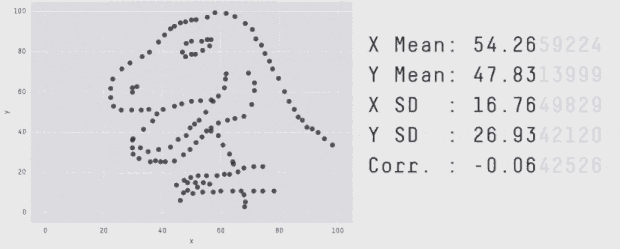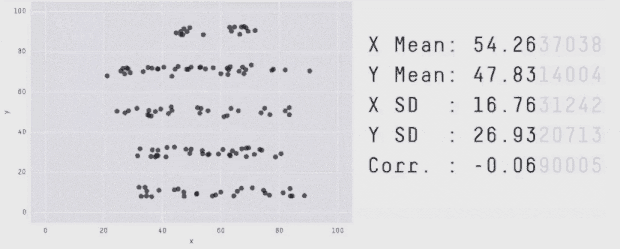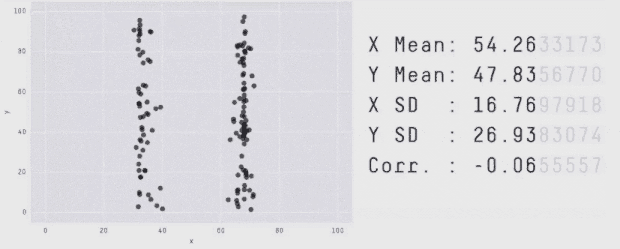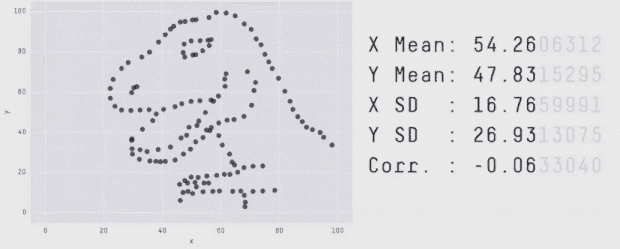
نمونههای بیشتر
ما علاوه بر Datasaurus Dozen چند مجموعه داده نمونه دیگر نیز با استفاده از همین تکنیک اجرا کردیم. این نمونهها با تفصیلات بیشتر در این مقاله توضیح داده شدهاند و دادههای آنها را برای بصری سازی میتوانید از اینجا دانلود نمایید.
یکی از جالبترین مشخصههای تکنیک حاضر این است که آن را میتوان برای بصری سازی نمودارهای پراکندگی غیر 2 بعدی و همچنین استفاده از مشخصات آماری فراتر از آمار توصیفی نیز به کار گرفت. در مثال زیر هر یک از مجموعه دادهها به صورت توزیع نرمالی از نقاط آغاز میشوند. نمودار جعبهای زیر هر شکل یک «نمودار جعبهای توکی» استاندارد است که مقادیر چارک نخست، میانه و چارک سوم را روی جعبه نمایش میدهد و میلهها موقعیت دورترین نقاط دادهای را درون محدوده 1.5 چارکی از چارک اول تا سوم نشان میدهند. نمودارهای جعبهای به طور عمده برای نمایش توزیع مجموعه دادهها مورد استفاده قرار میگیرند و کارکرد آنها بهتر از نمایش صرف مقادیر میانگین و میانه است. با این حال در اینجا میتوانیم ببینیم که با تغییر نقاط، نمودار جعبهای یکسان باقی میمانند.

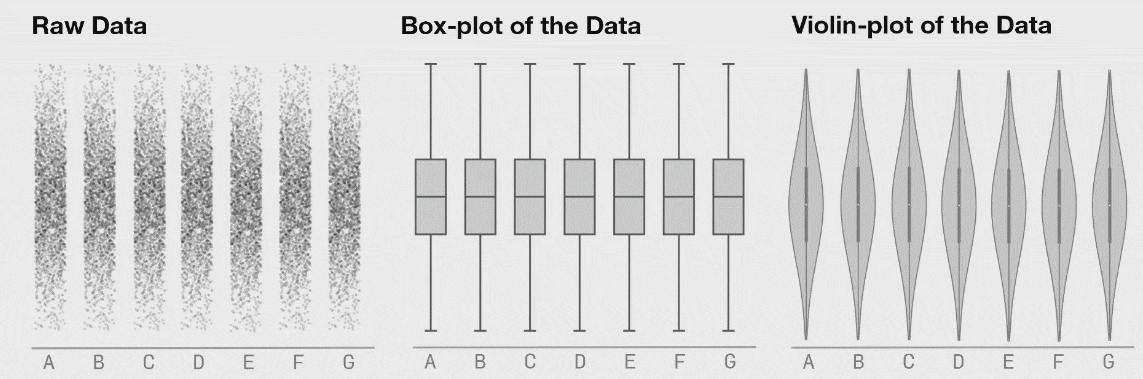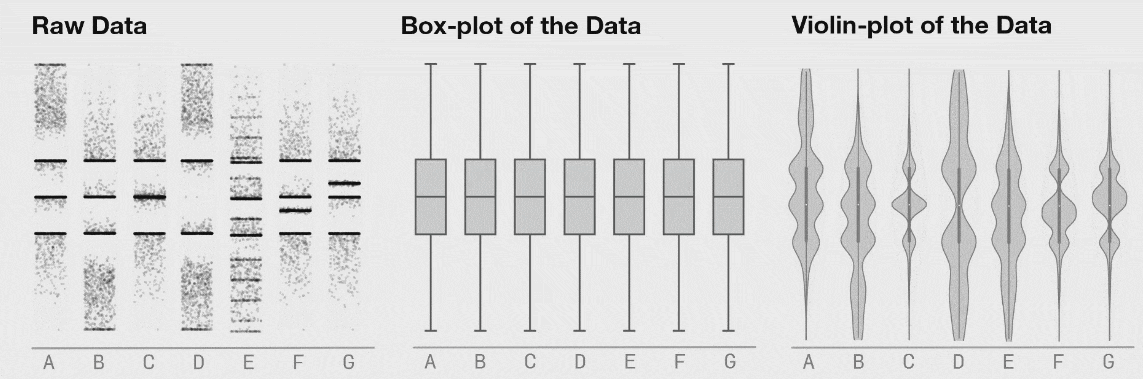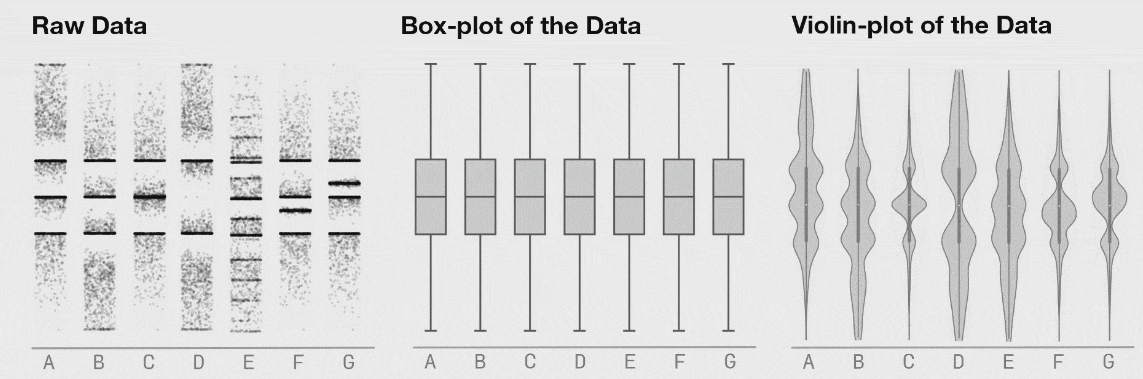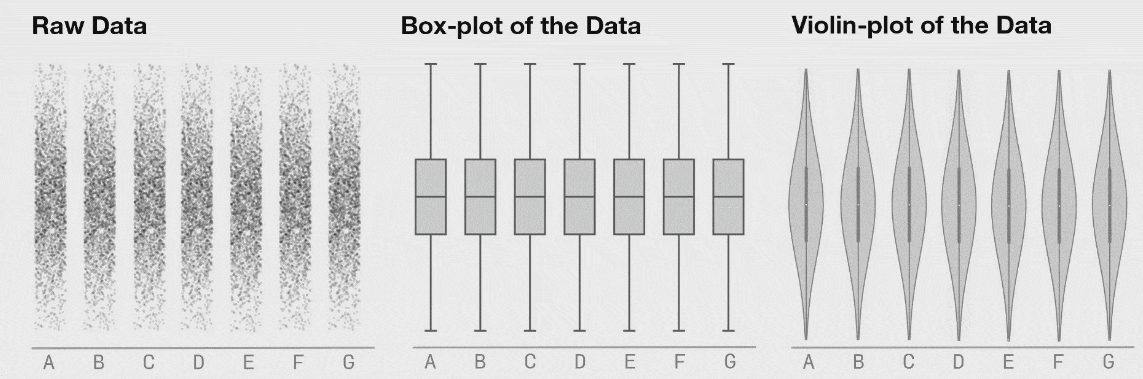
روش دیگر برای نمایش توزیع 1-بعدی این است که یک مجموعه داده را در هفت دستهبندی (شکل زیر را ببینید). این دادهها در هر دسته در طی زمان تغییر انتقال مییابند که در نمایش دادههای «خام» کاملاً به وضوح قابل مشاهده است، اما نمودارهای جعبهای یکسان میمانند. نمودارهای ویولون روش بهتری نسبت به نمودار جعبهای سنتی برای نمایش توزیع یک مجموعه داده با تفصیلات بیشتر است. این بدان معنی نیست که یک نمودار جعبهای هرگز مناسب نخواهد بود؛ اما اگر میخواهید از یک نمودار جعبهای استفاده کنید، ابتدا مطمئن شوید دادههای تشکیل دهنده به ترتیبی توزیع یافتهاند که اطلاعات مهم پنهان نمیمانند.
مجموعه دادهها و کد
مجموعه دادههای ارائه شده در این صفحه (و در مقاله) برای دانلود موجود هستند. کد منبع پایتون را از اینجا میتوانید دانلود کنید. تلاش شده است تا موارد اضافی تا حد امکان از کد حذف شوند تا خوانایی آن افزایش یابد.
اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز ملاحظه نمایید:
- آموزش نمودار مولفه (Component) در مدل سازی UML
- نمودارهای تصویری – به زبان ساده
- آموزش مهارتهای اساسی کامپیوتر
- آموزش نمایش داده ها و ترسیم نمودار در اکسل
- نمودارهای پراکندگی – به زبان ساده
- نمایش و رسم نمودار برای دادهها — معرفی و کاربردها
- آموزش اتوکد (AutoCAD)
==













