الگوریتم پریم – به زبان ساده

«الگوریتم پریم» (Prim’s Algorithm)، یک الگوریتم «حریصانه» (Greedy) است. این الگوریتم، با یک درخت پوشای کمینه (Minimum Spanning Tree | MST) خالی آغاز به کار می‌کند. هدف آن است که دو مجموعه از راس‌ها ساخته شوند. اولین مجموعه، شامل راس‌هایی است که در حال حاضر در درخت پوشای کمینه قرار دارند. مجموعه دیگر، شامل راس‌هایی است که هنوز در درخت قرار ندارند. در هر گام، الگوریتم همه یال‌هایی که دو مجموعه را به یکدیگر متصل می‌کنند در نظر می‌گیرد و یال دارای حداقل وزن را از میان این یال‌ها برمی‌گزیند. پس از انتخاب یال، دیگر نقطه نهایی یال را به پوشه حاوی راس‌های MST انتقال می‌دهد.

در «نظریه گراف» (Graph Theory)، به گروهی از یال‌ها که دو مجموعه از راس‌ها را در گراف به یکدیگر متصل می‌کنند «برش» (Cut) گفته می‌شود. بنابراین، در هر گام از الگوریتم پریم، می‌توان برشی را پیدا (از دو مجموعه، یکی حاوی یال‌هایی که در حال حاضر در MST قرار دارند و دیگری حاوی سایر راس‌ها است) و یال با کمترین وزن را از برش انتخاب کرد و در مجموعه MST قرار داد (مجموعه حاوی راس‌هایی است که در حال حاضر در درخت پوشای کمینه پریم قرار دارند). در ادامه، روش کار الگوریتم پریم مورد بررسی قرار گرفته و سپس، کد پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C ،C، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) ارائه شده است.

روش کار الگوریتم پریم

ایده نهفته در پس الگوریتم پریم ساده است. درخت پوشا یعنی همه راس‌ها باید به یکدیگر متصل باشند. بنابراین، دو مجموعه مجزا (که در بالا تشریح شدند) باید برای ساخت یک درخت پوشا به یکدیگر متصل شوند. همچنین، باید با یال‌های دارای حداقل وزن به یکدیگر متصل شوند تا درخت پوشای کمینه ساخته شود.

الگوریتم پریم

1. مجموعه mstSet را بساز که راس‌هایی که در حال حاضر در درخت پوشای کمینه پریم وجود دارند در آن قرار دارد.
2. یک مقدار کلیدی را به همه راس‌ها در گراف ورودی تخصیص بده. همه مقادیر کلیدی را با INFINITE مقداردهی اولیه کن. مقدار کلیدی صفر (۰) را به اولین راس تخصیص بده، تا این راس در ابتدا انتخاب شود.
3. تا هنگامی که mstSet حاوی همه راس‌ها نیست:
   • راس u را که در mstSet قرار ندارد و کمترین مقدار کلیدی را دارا است انتخاب کن.
   • u را در mstSet قرار بده.
   • مقادیر کلیدی همه راس‌های مجاوری u را به روز رسانی کن. برای به روز رسانی این مقادیر کلیدی، در همه راس‌های مجاور تکرار را انجام بده. برای هر راس مجاور v، اگر وزن یال u-v کمتر از مقدار کلیدی پیشین v است، مقادیر کلیدی را به عنوان وزن u-v به روز رسانی کن.

هدف از استفاده از مقادیر کلیدی، انتخاب یال دارای کمترین وزن از برش است. مقادیر کلیدی تنها برای راس‌هایی استفاده می‌شوند که در MST قرار ندارند، مقدار کلیدی برای این راس‌ها نشان‌گر حداقل وزنی است که آن‌ها را به مجموعه قرار داده شده در MST متصل می‌کند. برای درک بهتر موضوع، در ادامه مثالی ارائه شده است. گراف زیر با ۸ راس مفروض است.

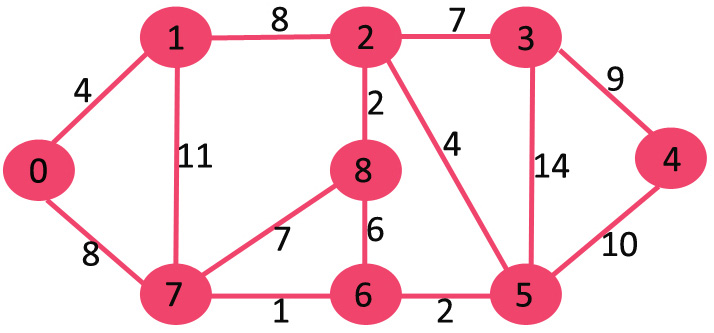
مجموعه mstSet به صورت اولیه خالی است و کلیدهای تخصیص پیدا کرده به راس‌ها به صورت $$\{ 0, INF, INF, INF, INF, INF, INF, INF \}$$ هستند؛ INF در این مجموعه به معنای نامتناهی است. اکنون، راسی با کمترین مقدار کلیدی انتخاب می‌شود. راس ۰ انتخاب می‌شود که در mstSet قرار ندارد. پس از قرار دادن ۰ در مجموعه mstSet، مقادیر کلیدی راس‌های مجاور آن به روز رسانی می‌شوند. راس‌های مجاور ۰، راس‌های ۱ و ۷ هستند. مقادیر کلیدی ۱ و ۷ با ۴ و ۸ به روز رسانی می‌شوند. زیرگراف زیر، نشانگر راس‌ها و مقادیر کلیدی آن‌ها است. در شکل زیر، تنها راس‌هایی با مقادیر کلیدی متناهی نمایش داده شده‌اند. راس‌هایی که در MST قرار دارند، به رنگ سبز نمایش داده شده‌اند.

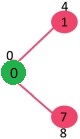
راسی با حداقل مقدار کلیدی که در حال حاضر در MST (درخت پوشای کمینه) قرار ندارد (در مجموعه mstSET قرار ندارد) و دارای وزن کمترین است (مقدار کلیدی) انتخاب می‌شود. بنابراین، در این وهله، راس 1 انتخاب و به mstSet اضافه می‌شود. بنابراین، mstSet اکنون به صورت {0, 1} است. مقادیر کلیدی از راس‌های مجاور ۱ به روز رسانی می‌شوند. مقدار کلیدی راس ۲ برابر با ۸ است.

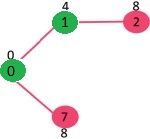
راسی با حداقل مقدار کلیدی که در حال حاضر در MST قرار ندارد (در mstSET قرار ندارد) انتخاب می‌شود. همچنین، می‌توان راس ۷ یا ۲ را انتخاب کرد. در حال حاضر، راس ۷ انتخاب می‌شود. بنابراین، mstSet اکنون به صورت $${0, 1, 7}$$ خواهد بود. مقادیر کلیدی راس‌های مجاور ۷ به روز رسانی می‌شوند. مقدار کلیدی راس‌های ۶ و ۸ متناهی می‌شوند (به ترتیب ۱ و ۷).

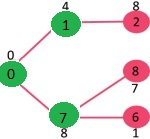
راس با حداقل مقدار کلیدی که در حال حاضر در MST قرار ندارد (در mstSET قرار ندارد) انتخاب می‌شود. بنابراین، mstSet اکنون به صورت {0, 1, 7, 6} خواهد بود. مقدار کلیدهای راس‌های مجاور به روز رسانی می‌شود. مقدار کلیدی راس ۵ و ۸ به روز رسانی می‌شود.

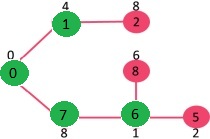
گام‌های بالا، تا هنگامی که mstSet شامل همه راس‌های گراف نشده است، ادامه خواهد داشت. در نهایت، گراف زیر حاصل خواهد شد.

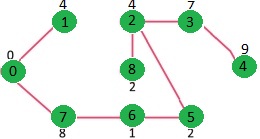
برنامه الگوریتم پریم

از یک آرایه بولی []mstSet برای ارائه مجموعه‌ای از راس‌هایی که در درخت پوشای کمینه قرار دارند استفاده می‌شود. اگر مقدار [mstSet[v درست (True) باشد، راس v در MST قرار دارد، در غیر این صورت، در درخت پوشای کمینه نیست. کلید آرایه []key برای ذخیره‌سازی مقادیر کلیدی همه راس‌ها مورد استفاده قرار می‌گیرد. آرایه دیگر []parent برای ذخیره‌سازی اندیس‌های راس‌های (گره‌های) والد در MST مورد استفاده قرار می‌گیرد. آرایه والد، آرایه خروجی است که برای نمایش درخت پوشای کمینه (MST) ساخته شده مورد استفاده قرار می‌گیرد.

برنامه الگوریتم پریم در ++C

فیلم آموزش ساختمان داده ها و پیاده سازی در سی پلاس پلاس C++‎ در فرادرس

کلیک کنید

برنامه الگوریتم پریم در C

برنامه الگوریتم پریم در جاوا

فیلم آموزش الگوریتم ها و روش های جست و جو در آرایه (رایگان) در فرادرس

کلیک کنید

برنامه الگوریتم پریم در پایتون

برنامه الگوریتم پریم در #C

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

پیچیدگی زمانی روش مورد استفاده در کدهای بالا، از درجه (O(V² است. اگر گراف ورودی با استفاده از لیست مجاورت نمایش داده شود، پیچیدگی زمانی الگوریتم پریم را می‌توان به کمک «هرم دودویی» (Binary Heap) به درجه (O(E log V کاهش داد.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی

^^