پیاده سازی الگوریتم KNN با پایتون — راهنمای کاربردی

الگوریتم KNN یا همان الگوریتم K-نزدیک ترین همسایگی (K-Nearest Neighbors) یکی از ساده‌ترین و در عین حال پرکاربردترین الگوریتم‌های یادگیری نظارت شده (Supervised Learning) در حوزه یادگیری ماشین است. KNN هم برای مسائل رگرسیون (Regression) و هم مسائل طبقه بندی (دسته بندی | Classification) کاربرد دارد. در این مطلب قصد داریم، ضمن آشنایی با این الگوریتم پرکاربرد، پیاده سازی الگوریتم KNN با پایتون را به صورت گام به گام انجام داده و برای حل یک مسئله‌ طبقه بندی از آن استفاده کنیم.

پیش از شروع پیاده سازی الگوریتم KNN با پایتون ، ابتدا بهتر است به این سوال پاسخ داده شود که KNN چیست؟

الگوریتم KNN چیست ؟

KNN سرنامی برای عبارت «K-Nearest Neighbors» به معنی «K نزدیک‌ترین همسایگی» است که نام این الگوریتم اشاره به شیوه کار آن دارد. برای مثال، فرض می‌شود مقدار K برابر 10 در نظر گرفته شود. در این شرایط، برای پیش‌بینی دسته هر داده مورد نظر، ابتدا 10 داده‌ مشابه انتخاب می‌شوند که دارای کمترین فاصله با داده مورد نظر هستند. سپس، برچسب (Label) این ۱۰ داده بررسی می‌شود و نوع دسته هر کدام از این داده‌ها که دارای بیش‌ترین تکرار باشد، به عنوان پاسخ پیش‌بینی نوع دسته داده ورودی انتخاب می‌شود.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

در ادامه این مقاله به پیاده سازی الگوریتم KNN با پایتون پرداخته شده است.

پیاده سازی الگوریتم KNN با پایتون

در این بخش، به صورت گام به گام به آموزش پیاده سازی الگوریتم KNN با پایتون پرداخته شده است. در ابتدا باید کتابخانه‌های مورد نیاز برای پیاده سازی KNN را فراخوانی کرد.

فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین در فرادرس

کلیک کنید

فراخوانی کتابخانه‌های مورد نیاز برای پیاده سازی الگوریتم KNN با پایتون

برای شروع کدنویسی، ابتدا باید کتابخانه‌های مورد نیاز را فراخوانی کرد:

1import numpy as np
2import sklearn.metrics as met
3import matplotlib.pyplot as plt
4import sklearn.model_selection as ms

ایجاد مجموعه داده مصنوعی برای پیاده سازی الگوریتم KNN با پایتون

باید یک مجموعه داده ایجاد شود تا بتوان KNN را روی آن‌ها پیاده سازی کرد. بنابراین، برای تولید داده‌های مصنوعی تابع CreateDataset به صورت زیر تعریف می‌شود:

1def CreateDataset(Cs, nD, S):
2    nC = len(Cs)
3    N = nD * nC
4    X = np.zeros((N, 2))
5    Y = np.zeros((N, 1))
6    for i in range(0, nD):
7        for j in range(0, nC):
8            X[nC*i + j, 0] = Cs[j, 0] + np.random.randn() / S
9            X[nC*i + j, 1] = Cs[j, 1] + np.random.randn() / S
10            Y[nC*i + j, 0] = j
11    return X, Y

در کدهای فوق، تابع CreateDataset، یک مجموعه داده حول مختصات مرکزهای دسته ایجاد می‌کند. مرکزهای دسته‌ به عنوان ورودی به تابع ارجاع داده می‌شوند.

تعریف مراکز دسته برای داده‌های مصنوعی

یکی از ورودی‌های تابع CreateDataset، آرایه‌ای حاوی مراکز دسته است. بنابراین، پس از تعریف تابع CreateDataset باید تعدادی مرکز دسته برای تولید داده‌های مصنوعی تعریف شود:

1Cs = np.array([[-0.5, 1], [1.5, 0], [-1, -1.5], [-2, 2.5], [0.5, 2]])

تعیین تعداد داده‌های مصنوعی و میزان پراکندگی آن‌ها

اکنون باید یک متغیر به نام nD برای تعداد داده در هر دسته و متغیر دیگری به نام S، برای تعیین میزان پراکندگی داده‌ها حول مراکز تعریف و آن‌ها را مقداردهی کرد:

1nD = 140
2S = 2.9

باید توجه داشت که با افزایش S، شدت پراکندگی داده‌ها کاهش خواهد یافت.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

فراخوانی تابع CreateDateset و تولید داده‌های مصنوعی

با آماده شدن آرگومان‌های ورودی، اکنون می‌توان تابع CreateDateset را فراخوانی کرد:

1X, Y = CreateDataset(Cs, nD, S)

خروجی این تابع، دو آرایه خواهد بود که X شامل مختصات داده و Y شامل برچسب متناظر با آن داده است. با توجه به اینکه 5 مرکز دسته تعریف شده است، تعداد داده‌ها به صورت $$5 \times nD = 700$$ محاسبه می‌شود.

رسم نمودار توزیعی داده‌های مصنوعی تولید شده

در نهایت، کدهای مربوط به رسم نمودار توزیع داده‌های تولید شده از کدهای زیر استفاده شده است:

1plt.style.use('ggplot')
2plt.scatter(X[:, 0], X[:, 1],c = Y[:, 0], s = 9, label = 'Data')
3plt.scatter(Cs[:,0], Cs[:, 1], c = 'r', s = 100, label = 'Center', marker = '*')
4plt.title('Scatter Plot of Data')
5plt.xlabel('X1')
6plt.ylabel('X2')
7plt.legend()
8plt.show()

برای رسم داده‌هایی که دارای برچسب هستند، می‌توان به جای رنگ از برچسب داده‌ها استفاده کرد تا داده‌های مربوط به هر دسته، هم رنگ باشند. نمودار خروجی به صورت زیر است:

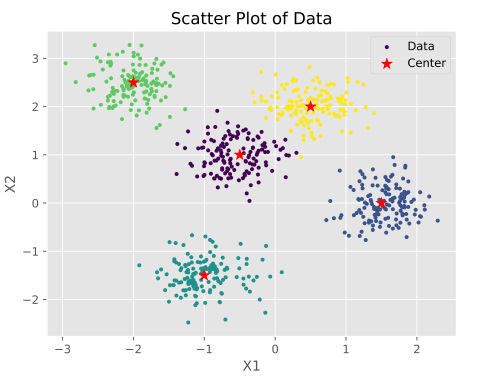
در ادامه آموزش پیاده سازی الگوریتم KNN با پایتون به چگونگی استفاده از فاصله اقلیدسی برای محاسبه فاصله میان داده‌ها برای تعیین K-نزدیک‌ترین همسایه‌ها پرداخته می‌شود. پیش از آن، مجموعه فیلم های آموزش هوش مصنوعی فرادرس به علاقه‌مندان معرفی شده است.

فیلم آموزش کتابخانه Matplotlib برای ترسیم و بصری سازی داده ها در پایتون در فرادرس

کلیک کنید

استفاده از فاصله اقلیدسی برای سنجش فاصله میان داده‌ها

در الگوریتم KNN، معیار شباهت دو داده، عکس فاصله آن دو داده از هم است. این فاصله می‌تواند به شیوه‌های مختلفی محاسبه شود. پرکاربردترین فاصله در این موارد، فاصله اقلیدسی (Euclidean Distance) است که با نام‌های L2-Distance و L2-Norm نیز شناخته می‌شود.

فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین در فرادرس

کلیک کنید

با فرض داشتن دو بردار $$x_i$$ و $$x_j$$ در یک فضای n-بُعدی، اگر بردار d_ij اختلاف عضو به عضو این دو بردار باشد، فاصله‌ی اقلیدسی بین این دو بردار به شکل زیر تعریف می‌شود:

$$Distance(x_i, x_j) = norm(d_{ij}) = \parallel d_{ij} \parallel =(\sum_{k=1}^{n} (d_{ij,k})^2)^{\frac{1}{2}}$$

پیاده سازی فاصله اقلیدسی در پایتون

برای استفاده از فاصله اقلیدسی در الگوریتم KNN، این تابع با نام Distance به صورت زیر در پایتون پیاده‌سازی می‌شود:

1def Distance(xi, xj):
2    dij = xi - xj
3    d = np.linalg.norm(dij)
4    return d

بنابراین، با استفاده از تابع Distance که در بالا پیاده‌سازی شده است، می‌توان فاصله‌ی بین دو بردار مورد نظر را یافت.

تعریف تابع محاسبه فاصله داده ورودی با سایر داده‌‌ها

اکنون نیاز به تابعی وجود دارد که با گرفتن یک بردار و یک مجموعه داده، فاصله‌ی بین تمامی داده‌ها با بردار ورودی را محاسبه کند. این تابع نیز به صورت زیر در پایتون قابل پیاده‌سازی است:

1def CalculateAllDistances(X, xi):
2    N = np.shape(X)[0] # Data Size
3    D = np.zeros(N) # Placeholder For Distances
4    for i in range(0, N):
5        xj = X[i]
6        D[i] = Distance(xi, xj)
7    return D

تابع CalculateAllDistances عملیات مورد نیاز را برای محاسبه فاصله هر یک از اعضای مجموعه داده $$X$$ از بردار $$x_i$$ انجام خواهد داد. در این تابع، ابتدا اندازه داده محاسبه و در متغیر N ذخیره می‌شود. سپس، یک آرایه خالی با اندازه N ساخته می‌شود تا در هر مرحله، فاصله بین بردار ورودی با داده متناظر حلقه، محاسبه و در آن ذخیره شود.

در نهایت، تابع CalculateAllDistances، آرایه D را در خروجی باز می‌گرداند. بنابراین، می‌توان فاصله بین هر بردار را با کل داده محاسبه کرد.

تعریف تابع KNN برای یافتن K تا از نزدیک ترین همسایه‌‌‌ها

اکنون در ادامه پیاده‌سازی الگوریتم KNN با پایتون باید K همسایه نزدیک را از بین کل فاصله‌های محاسبه شده پیدا کرد. بنابراین، یک تابع دیگر برای پیاده‌سازی این عملیات تعریف شده است:

1def KNN(K, X, xi):
2    D = CalculateAllDistances(X, xi) # Calculating Distances
3    A = np.argsort(D) # Sorted Args by Distance
4    Ns = A[:K] # K-Nearest Neighbors
5    return Ns

در تابع فوق (KNN)، موارد زیر به ترتیب اجرا می‌شود:

1. ابتدا تمامی فاصله‌ها محاسبه می‌شود.
2. سپس، درایه‌های ماتریس حاوی فاصله‌ها به نام D برحسب فاصله مرتب می‌شوند.
3. در نهایت K همسایه‌ی نزدیک که دارای کمترین فاصله هستند به کمک مرتب‌سازی انجام شده در مرحله قبل انتخاب می‌شوند.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

تعریف تابع Classify برای تعیین برچسب داده‌ها

حالا نیاز به تابعی وجود دارد که برچسب‌ داده‌های همسایه (که تا اینجا پیدا شده‌اند) را محاسبه و سپس، با استفاده از تابعی دیگر، بهترین دسته را انتخاب کند.

1def Classify(K, X, Y, xi):
2    Ns = KNN(K, X, xi) # Getting Neighbors Args
3    NsLabels = Y[Ns,0] # Getting Neighbors Labels
4    C = GetClass(NsLabels)
5    return C

در تابع فوق موارد زیر پیاده‌سازی شده‌اند:

1. ابتدا با استفاده از تابع KNN نزدیک‌ترین همسایه‌ها مشخص می‌شوند.
2. سپس برچسب همسایه‌ها از بردار Y استخراج می‌شود.
3. در نهایت، تصمیم‌گیری در مورد بهترین دسته، در تابع GetClass انجام شده است.

تعریف تابع GetClass برای تعیین دسته داده ورودی

اکنون باید تابع GetClass را تعریف کرد. این تابع برای تعیین دسته (کلاس) داده جدید بر اساس برچسب نزدیک‌ترین همسایه‌ها در تابع Classify (در کدهای فوق) استفاده شده است. به بیان دیگر، در تابع GetClass، باید با دریافت آرایه‌ی مربوط به برچسب همسایه‌ها در مورد داده جدید تصمیم‌گیری شود.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

در این تابع، پرتکرارترین برچسب انتخاب می‌شود و در شرایطی که تعداد دفعات تکرار دو یا چند Label باهم برابر است، دورترین همسایه حذف و دوباره مراحل انجام می‌شود، این عملیات با استفاده از حلقه While تا زمانی ادامه پیدا می‌کند که یکی از برچسب‌ها، از سایرین پرتکرارتر باشد. کدهای مربوط به تعریف این تابع در ادامه آمده است:

1def GetClass(NsLabels):
2    L = NsLabels.copy()
3    W = {}
4    for i in L:
5        if i not in W.keys():
6            W[i] = 1
7        else:
8            W[i] += 1
9    MaxN = max(W.values()) # Max Count of Most Frequent Label
10    BestClasses = []
11    for k, v in W.items():
12        if v == MaxN:
13            BestClasses.append(k)
14    while len(BestClasses) > 1: # While There is More Than One Best-Class
15        L = L[:-1] # Remove One Element From End
16        W = {}
17        for i in L:
18            if i not in W.keys():
19                W[i] = 1
20            else:
21                W[i] += 1
22        MaxN = max(W.values())
23        BestClasses = []
24        for k, v in W.items():
25            if v == MaxN:
26                BestClasses.append(k)
27    Best = BestClasses[0]
28    return Best

در تابع فوق، مراحل زیر به ترتیب انجام می‌شوند:

1. ایجاد یک کپی از ورودی و ذخیره آن در L
2. تولید یک دیکشنری خالی برای ذخیره دفعات تکرار هر برچسب
3. تکمیل‌ دیکشنری ساخته شده
4. محاسبه تعداد تکرار پرتکرارترین برچسب و ذخیره آن در MaxN
5. اضافه کردن تمامی برچسب‌هایی که به تعداد MaxN بار تکرار شده‌اند به لیست BestClasses
6. در صورتی که در لیست BestClasses بیش از یک عضو وجود داشته باشد (چندین دسته برنده وجود داشته باشد)، یک عضو از انتهای L حذف و مراحل 2 تا 6 تکرار می‌شوند. اگر در BestClasses تنها یک عضو وجود داشته باشد، آن عضو به عنوان دسته منتخب در خروجی باز گردانده خواهد شد.

اجرا و آزمایش پیاده سازی الگوریتم الگوریتم KNN با پایتون

اکنون، تمام برنامه پیاده‌سازی الگوریتم KNN در پایتون آماده شده است و می‌توان از آن استفاده کرد. برای این کار، ابتدا باید داده‌ها را به دو بخش Test و Train تقسیم کرد.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

تقسیم داده‌ها به دو مجموعه داده‌های آموزشی و آزمایشی

تقسیم داده‌ها به دو مجموعه داده‌های آموزشی و آزمایشی به صورت زیر با پایتون انجام می‌شود:

1trX, teX, trY, teY = ms.train_test_split(X, Y, test_size = 0.2, random_state = 0)

اکنون می‌توان با استفاده از الگوریتم KNN پیش‌بینی‌هایی برای داده‌ها انجام داد و سپس نتایج را با مقادیر واقعی مقایسه کرد تا میزان دقت الگوریتم مشخص شود.

پیش‌بینی دسته داده‌ها برای مجموعه‌های Test و Train با استفاده از پیاده سازی انجام شده

برای این کار، ابتدا باید دو آرایه‌ی خالی به منظور ذخیره‌ی مقادیر پیش‌بینی شده ایجاد کرد:

1trPrediction = np.zeros(np.size(trY))
2tePrediction = np.zeros(np.size(teY))

اکنون می‌توان با استفاده از KNN و سایر توابعی که تا اینجا پیاده‌سازی شده‌اند، برای هر یک از داده‌ها پیش‌بینی را انجام داد و آن‌ها را در آرایه‌های فوق ذخیره کرد:

1K = 5
2
3# Making Predictions On Train Dataset
4for i in range(0, np.size(trY)):
5    xi = trX[i]
6    pred = Classify(K, trX, trY[:,0], xi)
7    trPrediction[i] = pred
8
9# Making Predictions On Test Dataset
10for i in range(0, np.size(teY)):
11    xi = teX[i]
12    pred = Classify(K, trX, trY[:,0], xi)
13    tePrediction[i] = pred

به این ترتیب، پیش‌بینی‌هایی برای هر دو مجموعه داده آموزشی (Train) و آزمایشی (Test) انجام شد. باید توجه داشت که در تابع Classify تنها می‌توان از داده‌های آموزشی برای $$X$$ و $$Y$$ استفاده کرد.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

سنجش عملکرد پیاده سازی الگوریتم KNN با پایتون

حالا برای بررسی عملکرد الگوریتم KNN ، باید میزان دقت (Accuracy) را برای هر دو مجموعه داده آموزش و تست محاسبه کرد:

1trAccuracy = met.accuracy_score(trY, trPrediction) # Accuracy On Train Dataset
2teAccuracy = met.accuracy_score(teY, tePrediction) # Accuracy On Test Dataset

مقادیر محاسبه شده در خروجی برای میزان دقت مجموعه داده آموزشی، 0.9982 یا ۹۹.۸۲ درصد و دقت داده‌های آزمایشی برابر با ۱ یا ۱۰۰ درصد است.

تحلیل نتیجه سنجش

همان‌طور که ملاحظه می‌شود، نتایج مطلوبی حاصل شده است. البته باید توجه داشت که مجموعه داده استفاده شده در این برنامه، مجموعه کوچک و ساده‌ای به حساب می‌آید. در داده‌های واقعی که دارای پیچیدگی بیشتری هستند، نمی‌توان به این سطح از دقت دست یافت.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

نکته دیگری که وجود دارد، بهتر بودن دقت داده‌های آزمایشی نسبت به دقت محاسبه شده برای داده‌های آموزشی است. دلیل این مسئله را می‌توان کوچک بودن مجموعه داده تست و همچنین پراکندگی کم داده‌ها حول مراکز در نظر گرفت.

با افزایش میزان پراکندگی داده‌ها چه تغییری در سنجش عملکرد KNN به وجود می‌آید؟

با کاهش S به عدد 2 (افزایش میزان پراکندگی داده‌ها)، نمودار توزیعی مجموعه داده به صورت زیر تغییر می‌کند:

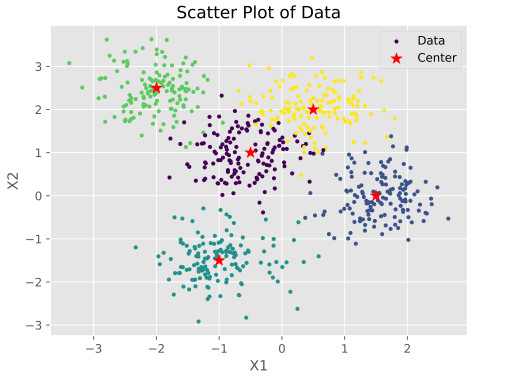
با تغییر میزان پراکندگی داده‌ها،‌ دقت استفاده از داده‌های آموزشی برابر با 0.9696 یا همان ۹۶.۹۶ درصد و دقت داده‌های آزمایشی هم 0.9357 یا ۹۳.۵۷ درصد خواهد بود. بنابراین، با افزایش میزان پراکندگی و زیاد شدن درهم‌رفتگی دسته‌ها، دقت الگوریتم نیز کاهش می‌یابد. البته باید توجه داشت که تنها معیار برای بررسی عملکرد طبقه‌بند (Classifier)، محاسبه دقت (Accuracy) نیست و می‌توان از ماتریس درهم‌ریختگی (Confusion Matrix) نیز برای بررسی دقیق‌تر عملکرد الگوریتم KNN و سایر الگوریتم‌ها استفاده کرد.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

جمع‌بندی

در مقاله آموزش پیاده سازی الگوریتم KNN با پایتون ، ابتدا به طور مختصر با یک مثال به چیستی این الگوریتم پرداخته شد و سپس پیاده سازی الگوریتم KNN با پایتون به صورت گام به گام با بیانی ساده و به همراه کلیه کدهای مربوطه ارائه شد. در پایان نیز الگوریتم پیاده سازی شده با محاسبه میزان دقت و تحلیل دقت محاسبه شده مورد سنجش و تجزیه-تحلیل قرار گرفت. همچنین، دوره‌های آموزشی متعددی پیرامون مباحث مختلف هوش مصنوعی و یادگیری ماشین در این مقاله معرفی شده است.