پیاده سازی رگرسیون لجستیک در پایتون — راهنمای گام به گام

در آموزش‌های پیشین مجله فرادرس با رگرسیون لجستیک آشنا شدیم. در این آموزش، به پیاده سازی رگرسیون لجستیک در پایتون می‌پردازیم.

رگرسیون لجستیک چیست؟

مدل رگرسیون لجستیک، یکی از ساده‌ترین مدل‌ها برای طبقه‌بندی است. در این روش ابتدا ترکیبی خطی از ویژگی‌های ورودی ایجاد می‌شود:

$$\large L(x)=b+w_{1} x_{1}+w_{2} x_{2} \ldots+w_{n} x_{n}=b+\sum_{i=1}^{n} w_{i} x_{i}$$

که می‌توان این رابطه را به شکل برداری نیز توصیف کرد:

$$\large L(x)=b+x \cdot w^{T }$$

سپس خروجی این ترکیب خطی، وارد «تابع سیگموئید» (Sigmoid Function) یا تابع لجستیک می‌شود:

$$\large O(x)=\frac{1}{1+e^{-L(x)}}$$

به این ترتیب، خروجی مدل عددی بین ۰ و ۱ خواهد بود. با تعیین یک مرز $$\hat{y}$$، داده‌هایی که مقدار آن‌ها خروجی کمتر از ۰٫۵ باشد، به کلاس ۰ و داده‌هایی که خروجی آن‌ها بیشتر از ۰٫۵ باشد به کلاس ۱ اختصاص می‌یابند.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

آموزش مدل رگرسیون لجستیک

برای آموزش مدل رگرسیون لجستیک، ابتدا برای مدل یک تابع هزینه به شکل زیر تعریف می‌کنیم:

$$\large J=\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}\right)^{2}$$

برای آموزش این مدل نیز می‌توان از الگوریتم گرادیان کاهشی استفاده کرد:

$$\large \begin{aligned} &\Delta w_{i}=-\eta \cdot \frac{\partial J}{\partial w_{i}} \\ &\Delta b=-\eta \cdot \frac{\partial J}{\partial b} \end{aligned}$$

می‌توان گرادیان تابع هزینه نسبت به هر پارامتر را محسابه کرده و در رابطه قرار داد که در نهایت منجر به رابطه‌ای مستقیم برای به‌روزرسانی وزن‌ها خواهد شد.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های برنامه نویسی پایتون (Python) — مقدماتی تا پیشرفته + اینجا کلیک کنید.

پیاده سازی رگرسیون لجستیک در پایتون

برای پیاده سازی رگرسیون لجستیک در پایتون باید چند مرحله را طی کنیم که در ادامه به آن‌ها می‌پردازیم.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

فراخوانی کتابخانه‌ها

ابتدا و در اولین گام از پیاده سازی رگرسیون لجستیک در پایتون کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

1import numpy as np
2import sklearn.metrics as met
3import matplotlib.pyplot as plt
4import sklearn.linear_model as lm

این کتابخانه‌ها به ترتیب برای کار با آرایه، محاسبه معیارهای ارزیابی، رسم نمودار و ایجاد مدل‌های خطی استفاده خواهند شد.

حال Seed و Style را تنظیم می‌کنیم:

1np.random.seed(0)
2plt.style.use('ggplot')

تولید داده

در این مرحله نیاز است تا مجموعه داده‌ای برای آموزش مدل ایجاد کنیم. یک مجموعه داده با ۲ ویژگی ورودی و ۲ دسته، با شرایط زیر ایجاد می‌کنیم:

$$\large \begin{align} &-1 \leq x_{1}<+1 \\ &-1 \leq x_{2}<+1 \\ & y=0.5 \times \operatorname{sign}\left(1.6 \times x_{1}-1.2 \times x_{2}+0.4\right)-0.5 \end{align}$$

برای ایجاد این مجموعه داده، به شکل زیر عمل می‌کنیم:

1N = 500
2X = np.random.uniform(-1, +1, size=(N, 2))
3Y = 0.5 * np.sign(1.6*X[:, 0] - 1.2*X[:, 1] + 0.4) + 0.5

متغیر N نشان‌دهنده اندازه مجموعه داده می‌شود. سپس ماتریس X با دو ستون به صورت تصادفی تولید می‌شود.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

در نهایت رابطه گفته شده برای تعیین Labelها را اعمال می‌کنیم.

مصورسازی مجموعه داده تولیدشده

برای بررسی شرایط مجموعه داده، نیاز است تا آن را رسم کنیم. برای این کار به شکل زیر عمل می‌کنیم:

1plt.scatter(X[:, 0], X[:, 1], c=Y, s=12)
2plt.title('Data')
3plt.xlabel('X1')
4plt.ylabel('X2')
5plt.show()

به این ترتیب، یک Scatter Plot خواهیم داشت که داده‌های هر دسته با رنگ مخصوص از باقی داده‌ها جدا شده‌اند.

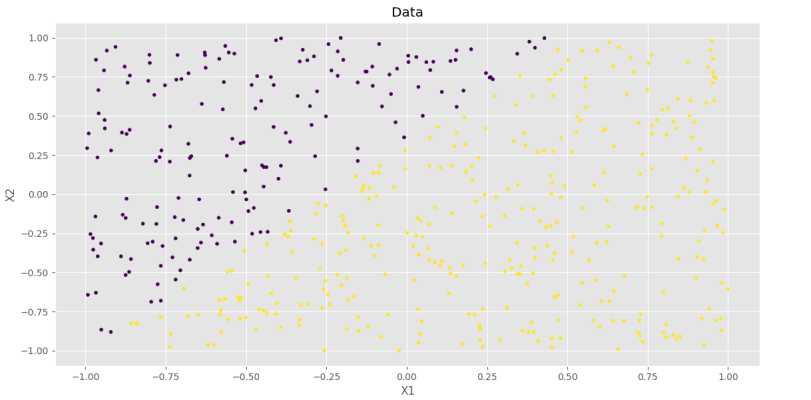
به این ترتیب، مجموعه داده به درستی ایجاد و نمایش داده می‌شود.

فیلم آموزش یادگیری عمیق با کتابخانه پای تورچ PyTorch در پایتون در فرادرس

کلیک کنید

پیاده‌سازی مدل

حال باید مدل رگرسیون لجستیک را ایجاد کنیم. برای این کار ابتدا یک تابع تعریف می‌کنیم که با گرفتن داده ورودی و پارامترها، خروجی مدل را محاسبه کند:

1def Model(W:np.ndarray, B:float, X:np.ndarray):
2    L = B + np.dot(X, W)
3    O = 1 / (1 + np.exp(-L))
4    return O

به این ترتیب، ابتدا ترکیب خطی از بردار ورودی محاسبه می‌شود. سپس تابع سیگموئید اعمال و خروجی مدل حاصل می‌شود.

حال باید برای وزن‌ها و بایاس، مقداردهی اولیه کنیم:

1W = np.random.uniform(-1, +1, size=(2, 1))
2B = np.random.uniform(-1, +1)

به این ترتیب، مقادیر اولیه برای پارامتر‌ها نیز تعیین می‌شود.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

حال نرخ یادگیری و تعداد مراحل آموزش مدل را تعیین می‌کنیم:

1lr = 1e-3
2nIteration = 10

حال می‌توان هسته اصلی مربوط به آموزش مدل را پیاده‌سازی کرد.

باید به ازای هم مرحله و به ازای هر داده پارامترهای مدل را به‌روزرسانی کنیم:

1for Iteration in range(nIteration):
2    for x, y in zip(X, Y):

حال باید مقدار گرادیان تابع هزینه نسبت به وزن‌ها را با استفاده از تنها یک داده محاسبه کنیم:

$$\large \begin{align} \Delta w_{i} &=-\eta \cdot \frac{\partial J}{\partial w_{i}}=-\eta \cdot \frac{\partial(y-\hat{y})^{2}}{\partial w_{i}}=-\eta \cdot 2 \cdot(y-\hat{y}) \cdot \frac{-\partial \hat{y}}{\partial w_{i}} \\ &=2 \cdot \eta \cdot e \cdot \frac{\partial\left(\frac{1}{1+e^{-L(x)}}\right)}{\partial w_{i}}=2 \cdot \eta \cdot e \cdot \frac{\partial\left(1+e^{-L(x)}\right)^{-1}}{\partial w_{i}} \\ &=-2 \cdot \eta \cdot e \cdot\left(1+e^{-L(x)}\right)^{-2} \cdot \frac{\partial e^{-L(x)}}{\partial w_{i}} \\ &=-2 \cdot \eta \cdot e\left(1+e^{-L(x)}\right)^{-2} \cdot e^{-L(x)} \cdot\left(-x_{i}\right) \\ &=2 \cdot \eta \cdot e \cdot x_{i} \cdot\left(1+e^{-L(x)}\right)^{-2} \cdot e^{-L(x)} \\& =2 \cdot \eta \cdot e \cdot x_{i} \cdot \hat{y} \cdot(1-\hat{y}) \end{align}$$

به این ترتیب، رابطه نهایی برای به‌روزرسانی وزن‌ها به‌دست می‌آید. توجه داشته باشید که اگر عملیات فوق را برای بایاس نیز تکرار کنیم، به رابطه زیر خواهیم رسید:

$$\large \Delta b=-\eta \cdot \frac{\partial J}{\partial b}=2 \cdot \eta \cdot e \cdot \hat{y} \cdot(1-\hat{y})$$

حال روابط فوق را در برنامه اعمال می‌کنیم:

1for Iteration in range(nIteration):
2    for x, y in zip(X, Y):
3        #Training Model For Each Weight
4        for i in range(2):
5            p = Model(W, B, x)[0]
6            e = y - p
7            W[i] += 2 * lr * e * x[i] * p * (1 - p)
8        #Training Model For Bias
9        p = Model(W, B, x)[0]
10        e = y - p
11        B += 2 * lr * e * p * (1 - p)

به این ترتیب، بخش مربوط به آموزش مدل نیز کامل می‌شود. برای بررسی وضعیت مدل در هر مرحله، مقدار تابع هزینه و دقت را نیز محاسبه و نمایش می‌دهیم.

برای این منظور، تابع هزینه را به شکل زیر پیاده‌سازی می‌کنیم:

1def Cost(W:np.ndarray, B:float, X:np.ndarray, Y:np.ndarray):
2    P = Model(W, B, X)[:, 0]
3    E = np.subtract(Y, P)
4    SE = np.power(E, 2)
5    MSE = np.mean(SE)
6    return MSE

برای پیاده‌سازی تابع دقت نیز به شکل زیر عمل می‌کنیم:

1def Accuracy(W:np.ndarray, B:float, X:np.ndarray, Y:np.ndarray):
2    P = np.round(Model(W, B, X))[:, 0]
3    A = 0
4    for y, p in zip(Y, P):
5        if y == p:
6            A += 1
7    A = 100 * A / Y.size
8    return A

به این ترتیب، از توابع مورد نظر استفاده می‌شود.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

حال توابع را داخل حلقه اصلی برنامه فراخوانی و نتایج را ذخیره می‌کنیم:

1Costs = np.zeros(nIteration + 1)
2Accuracies = np.zeros(nIteration + 1)
3
4c = Cost(W, B, X, Y)
5a = Accuracy(W, B, X, Y)
6Costs[0] = c
7Accuracies[0] = a
8print(f'Iteration: 0')
9print(f'Cost:      {c}')
10print(f'Accuracy:  {a} %')
11
12for Iteration in range(nIteration):
13    for x, y in zip(X, Y):
14        #Training Model For Each Weight
15        for i in range(2):
16            p = Model(W, B, x)[0]
17            e = y - p
18            W[i] += 2 * lr * e * x[i] * p * (1 - p)
19        #Training Model For Bias
20        p = Model(W, B, x)[0]
21        e = y - p
22        B += 2 * lr * e * p * (1 - p)
23    c = Cost(W, B, X, Y)
24    a = Accuracy(W, B, X, Y)
25    Costs[Iteration + ] = c
26    Accuracies[Iteration + 1] = a
27    print(f'Iteration: {Iteration + 1}')
28    print(f'Cost:      {c}')
29    print(f'Accuracy:  {a} %')

حال برنامه را اجرا می‌کنیم و نتایج به شکل زیر ظاهر می‌شود:

Iteration: 0
Cost:      0.19655169133879696
Accuracy:  71.8 %
Iteration: 1
Cost:      0.1551691465551683
Accuracy:  83.2 %
Iteration: 2
Cost:      0.13276571845816945
Accuracy:  89.0 %
...
...
...
Iteration: 9
Cost:      0.08266471377826749
Accuracy:  97.0 %
Iteration: 10
Cost:      0.07971907723185878
Accuracy:  96.8 %

به این ترتیب، مشاهده می‌کنیم که مدل از دقت ٪۷۱ شروع کرده و به دقت ٪۹۷ رسیده است. بنابراین الگوریتم گرادیان کاهشی به‌درستی عمل می‌کند.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

برای مصورسازی آموزش مدل، به شکل زیر دو نمودار برای دقت و تابع هزینه رسم می‌کنیم (برای نمایش بهتر آموزش مدل، تعداد مراحل آموزش را به ۵۰ افزایش و نرخ یادگیری را به ۰٫۰۰۵ کاهش می‌دهیم):

1plt.plot(Costs, ls='-', lw=1.2, marker='o', ms=3)
2plt.title('Model Cost Function Over Training')
3plt.xlabel('Iteration')
4plt.ylabel('Cost')
5plt.show()
6
7plt.plot(Accuracies, ls='-', lw=1.2, marker='o', ms=3)
8plt.title('Model Accuracy Over Training')
9plt.xlabel('Iteration')
10plt.ylabel('Accuracy (%)')
11plt.show()

که پس از اجرا، نمودارهای زیر حاصل می‌شود.

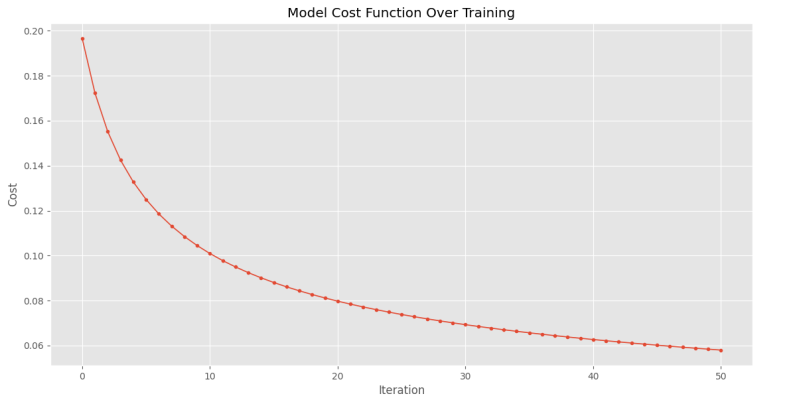
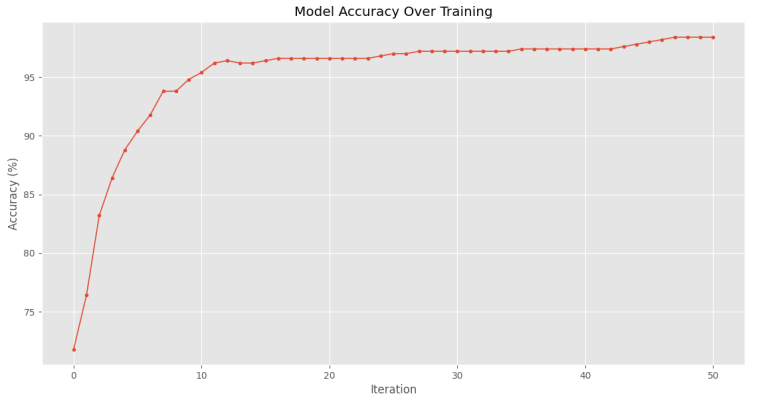
به این ترتیب، مشاهده می‌کنیم که مدل روند آموزش خود را به خوبی طی کرده و به‌درستی آموزش دیده است.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

اگر در انتهای برنامه، پارامترها را پرینت کنیم، به نتایج زیر می‌رسیم:

W = [[ 3.13467116],
     [-2.30283268]]
B = 0.8992552752157723

در ظاهر، نتایج به دست آمده، با پارامترهای اولیه متفاوت است، نکته‌ای که وجود دارد این است که این اعداد مضربی مشخص از پارامترهای اولیه است. تمامی پارامترها، ۱٫۹۵ برابر پارامترهای انتخاب‌شده است. توجه داشته باشید که ضرب این اعداد در یک عدد مشخص، نتایج را تحت تأثیر قرار نمی‌دهد. به دلیل همین اتفاق، می‌توان از Regularization استفاده کرد.

استفاده از کدهای آماده پایتون

در کتابخانه Scikit-learn نیز امکاناتی برای انجام رگرسیون لجستیک وجود دارد.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

می‌توان برای ایجاد و آموزش این مدل، به شکل زیر عمل کرد:

1Model = lm.LogisticRegression()
2Model.fit(X, Y)

در نهایت، برای بررسی دقت خواهیم داشت:

1Accuracy = 100*Model.score(X, Y)
2print(f'Accuracy: {Accuracy} %')

پس از اجرا، دقت ٪۹۸٫۴ حاصل می‌شود که عددی بسیار نزدیک به الگوریتم پیاده‌سازی‌شده است.

برای بررسی‌های بیشتر در رابطه با نتایج مدل، می‌توان معیارهای بیشتری را بررسی کرد:

1P = Model.predict(X)
2CR = met.classification_report(Y, P)
3print(f'Classification Report:\n{CR}')

که خواهیم داشت:

Classification Report:
              precision    recall  f1-score   support

         0.0       1.00      0.95      0.98       176
         1.0       0.98      1.00      0.99       324

    accuracy                           0.98       500
   macro avg       0.99      0.98      0.98       500
weighted avg       0.98      0.98      0.98       500

به این ترتیب، عملکرد مناسب الگوریتم مشخص می‌شود.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

توجه داشته باشید که مجموعه داده نامتعادل است و در صورتی که به دقت مناسب در کلاس‌های مختلف نرسیم، می‌توانیم از روش‌های وزن‌دهی به دسته‌ها و یا تغییر مجموعه داده استفاده کرد.

برای استخراج پارامترهای مدل ایجادشده در Scikit-learn نیز می‌توانیم به شکل زیر عمل کنیم:

1print(f'W: {Model.coef_}')
2print(f'B: {Model.intercept_}')

که خواهیم داشت:

W: [[ 6.09624843 -4.51185994]]
B: [1.72291912]

این پارامترهای نیز ۳٫۸ برابر مقادیر انتخاب شده هستند.

با تغییر مدل به شکل زیر:

1Model = lm.LogisticRegression(penalty='l2', C=0.1)

پارامترها به ۱٫۵۴ برابر مقادیر اصلی می‌رسند:

W: [[ 2.47052748 -1.77922621]]
B: [0.89601296]

بنابراین، تعیین Regularization با C کوچک‌تر، الگوریتم را به انتخاب وزن‌های با اندازه کوچک‌تر سوق می‌دهد.

به این ترتیب، اهمیت Regularization نیز در تنظیم مدل کاملاً مشهود است.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

جمع‌بندی

در این مطلب با پیاده‌سازی رگرسیون لجستیک در پایتون آشنا شدیم و با ایجاد یک مجموعه داده مصنوعی، آن را پیاده‌سازی کرده و روی مجموعه داده آموزش دادیم. در نهایت نیز توابع آماده را بررسی کردیم.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای مطالعه بیشتر می‌توان موارد زیر را بررسی کرد:

1. تغییر کد پیاده‌سازی شده، برای آموزش مدل با توجه به وزن دسته‌ها
2. تغییر کد پیاده‌سازی شده، برای آموزش مدل Regularized
3. استفاده از نرخ یادگیری پویا در طول آموزش مدل
4. بررسی چگونگی محاسبه میزان اطمینان مدل از خروجی
5. بررسی ارتباط خروجی مدل رگرسیون لجستیک با احتمال اختصاص داده به هر کلاس
6. بررسی چگونگی طبقه‌بندی مجموعه داده‌ای با بیش از ۲ کلاس با استفاده از رگرسیون لجستیک