گسترده نویسی اعداد اعشاری — به زبان ساده + مثال و تمرین

در آموزشهای پیشین مجله فرادرس، با اعداد اعشاری آشنا شدیم. در این آموزش، به گسترده نویسی اعداد اعشاری میپردازیم.
گسترده نویسی اعداد صحیح
گسترده نویسی اعداد در ریاضیات به ما کمک میکند تا یک عدد صحیح را بهتر درک کنیم. برای مثال، عدد 875294831 را در نظر بگیرید. درک این عدد دشوار است. در اینجا، گسترده نویسی به ما کمک میکند تا هر یک از ارقام را بر اساس ارزش مکانی آنها درک کنیم. این موضوع را با یک مثال ساده توضیح میدهیم. عدد 324 را در نظر میگیریم و سعی کنیم شکل گسترشیافته آن را پیدا کنیم. 324 بهصورت گسترشیافته بهشکل ۴ + 20 + ۳۰۰ نوشته میشود. یعنی در این عدد ۳ صدتایی، ۲ دهتایی و ۴ یکی وجود دارد. بهراحتی میتوانیم ارزش و معنای هر رقم یک عدد را از طریق شکل گسترده آن درک کنیم.
تلاش برای یادگیری یک عدد با تعداد ارقام زیاد، بدون دانستن نحوه بیان آن به شکل گسترده بسیار دشوار است. گستردهنویسی به ما کمک میکند تا اجزای سازنده اعداد با ارقام بیشتر را بشناسیم. هریک از ارقام را میتوان به شکلهای متعدد 1، 10، 100، 1000 نوشت. اکنون با درک این موضوع، به یک مثال دیگر میپردازیم.
هر عدد در ریاضیات را میتوان بهصورت گسترده نوشت. نمایش عدد به صورت مجموع هر رقم در ارزش مکانی آن، شکل بازشده یا گسترده یک عدد است. نحوه خواندن اعداد، بهخوبی نوع گسترده نویسی آنها را ساده میکند.برای مثال، عدد ۱۲۷۸ را در نظر بگیرید. این عدد را اینگونه میخوانیم: هزار و دویست و هفتاد و هشت. بهخوبی مشخص است که این عدد از یک هزار بهاضافه ویست بهاضافه هفتاد به اضافه هشت تشکیل شده است و میتوان آن را بهفرم گسترده 1278 = ۸ + ۷۰ + ۲۰۰ + ۱۰۰۰ نوشت. در واقع، همان چیزی را که خواندهایم، نوشتهایم و بهجای «و» عمل ریاضی «+» ار قرار دادهایم.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
فرم گسترده به درک بهتر و خواندن صحیح اعداد اعداد بزرگ با ارقام زیاد کمک میکند. درک مستقیم عددی مانند 10030، گاهی اوقات دشوار است و میتوان آن را بهصورت گسترده 10030 = ۳۰ + ۱۰۰۰۰ نشان داد.
چند نمونه دیگر از فرم گسترده اعداد در جدول زیر ارائه شده است.
| یکان | دهگان | صدگان | هزارگان | دههزارگان | |
| ۳ | ۲ | ۷ | ۷۲۳ | ||
| ۳ | ۴ | ۲ | ۱ | ۱۲۴۳ | |
| ۹ | ۷ | ۶ | ۵ | ۵۶۷۹ | |
| ۶ | ۵ | ۴ | ۳ | ۲ | ۲۳۴۵۶ |
دیدیم که گسترده نویسی یک عدد صحیح، جداسازی اعداد بر اساس مقادیر مکانی است. شکل گسترده به ما کمک میکند تا ارزش مکانی هر رقم را در یک عدد بدانیم.
سه روش مختلف برای نوشتن اعداد به شکل گسترده وجود دارد. برای مثال، عدد 4537 را میتوان به سه شکل زیر نوشت:
- ۱ + ۳۰ + ۵۰۰ + ۴۰۰۰ = ۴۵۳۲
- (۱ × ۱) + (۱۰ × ۳) + (۱۰۰ × ۵) + (۱۰۰۰ × ۴) = ۴۵۳۱
- (یک تا × ۱) + (ده تا × ۳) + (صد تا × ۵) + (هزار تا × ۴) = 4537
روش گام به گامی وجود دارد که با استفاده از آن میتوانیم شکل گسترده اعداد را بهدست آوریم:
- عدد را به شکل استاندارد آن بنویسید.
- ارزش مکانی ارقام آن را تعیین کنید.
- رقم هر مکان را در ارزش مکانی آن ضرب کنید.
- حاصلضربها را با هم جمع کنید.
به این فرایند گسترده نویسی اعداد گفته میشود. اکنون یک مثال را بررسی میکنیم. میخواهیم عدد ۴۱۰۶ را بهصورت گسترده بنویسیم. گامهای زیر را طی میکنیم:
- عدد ۴۱۰۶ است.
- ارزش مکانی ارقام اینگونه است: یکان = ۶، دهگان = ۰، صدگان = ۱، هزارگان = ۴.
- ضرب ارقام در ارزش مکانیشان اینگونه خواهد بود: ۶ = ۱ × ۶ و ۰ = ۱۰ × ۰ و ۱۰۰ = ۱۰۰ × ۱ و ۴۰۰۰ = ۱۰۰۰ × ۴.
- اکنون حاصلضربها را با هم جمع میکنیم: ۶ + ۰ + ۱۰۰ + ۴۰۰۰ = ۴۱۰۶
اکنون که با گسترده نویسی اعداد صحیح آشنا شدهایم، میتوانیم به گسترده نویسی اعداد اعشاری بپردازیم. پیش از آن، اعداد اعشاری را مرور میکنیم.
مروری بر اعداد اعشاری
اعداد اعشاری (Decimal Numbers) اعدادی هستند که برای نمایش مقادیری به کار میروند که با اعداد شمارشی عادی نمیتوان آنها را بیان کرد. اعشار را با ممیز (یعنی تمایزدهنده) نمایش میدهیم. در دستور خط فارسی، علامت ممیز یک خط کوچک کج است. برای مثال، یک و نیم را به صورت ۱٫۵ مینویسیم. در زبان انگلیسی، ممیز را با نقطه نشان میدهند. مثلاً همان عدد یک و نیم در زبان انگلیسی بهصورت 1.5 نوشته میشود. توجه کنید که علامت کسر (/) با ممیز (٫) فرق دارد و اغلب بهاشتباه بهجای ممیز به کار میرود.
عدد ۶۴٫۰ را در نظر بگیرید که میدانیم همان ۶۴ است. این عدد به معنی ۶ دهتایی و ۴ یکی است و چون بخشهای کوچکتری از یک واحد ندارد، بعد از ممیز عددی قرار نمیگیرد. با یک مقایسه کوچک، مشاهده میکنیم که سمت راست ممیز، دهمها، صدمها، هزارمها و… و سمت چپ آن، دهگانها، صدگانها، هزارگانها و… را نمایش میدهند.
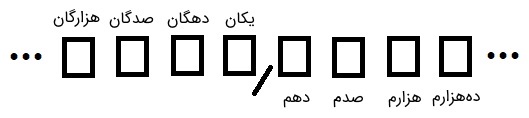
در سمت راستِ ممیزِ شکل بالا، هرچه به سمت راست میرویم، ارزش اعداد کم میشود. همچنین در سمت چپ ممیز، هرچه به سمت چپ میرویم، ارزش اعداد افزایش مییابد.دقت کنید که وقتی ممیز در عددی به کار میرود، باید آن را با عدد بدون ممیز تمایز دهیم. برای مثال، عدد ۱٫۰۰۰ همان یک است و ۱۰۰۰ نمایانگر عدد هزار است.
همچنین به یاد داشته باشید که برای اعشار تنها از علامت ممیز (٫) یا نقطه (.) استفاده میشود. گاهی علامتهایی مانند ویرگول انگلیسی (,) برای جدا کردن هزارگانها در اعداد بزرگ (مثلاً قیمتها) به کار میرود که نباید آن را با ممیز اشتباه گرفت. برای مثال ۱,۰۰۰,۰۰۰ یک میلیون را نشان میدهد که از علامت جداکننده «٬» برای جداسازی ارقام هزارتایی در آن استفاده شده است.
گسترده نویسی اعداد اعشاری
مانند اعداد صحیح، اعداد اعشاری را نیز میتوان بهصورت گسترده نوشت. برای گسترده نویسی اعداد اعشاری، ابتدا ارزش مکانی ارقام را قبل و بعد از اعشار مشخص میکنیم. با یک مثال، این موضوع را شرح میدهیم.
فرض کنید میخواهیم عدد اعشاری 0٫437 را بهصورت گسترده بنویسیم. ابتدا جدول ارزش مکانی را تشکیل میدهیم.
| هزارم | صدم | دهم | یکان |
| ۷ | ۳ | ۴ | 0 |
همانطور که میبینیم، با توجه به جدول بالا میتوان برای عدد ۰٫۴۳۷ چنین بیان کرد که از بخشهای زیر تشکیل شده است:
- ۷ تا یکهزارم
- ۳ تا یکصدم
- ۴ تا یکدهم
همین سه بخش را میتوان به شکل ریاضی زیر نوشت:
- ۰٫۰۰۱ × ۷
- ۰٫۰۱ × ۳
- ۰٫۱ × ۴
و حاصل این ضربها نیز بهراحتی نوشته میشود:
- ۰٫۰۰۷
- ۰٫۰۳
- ۰٫۴
بنابراین، عدد اعشاری ۰٫۴۳۷ را میتوان اینگونه گستردهنویسی کرد:
۰٫۰۰۷ + ۰٫۰۳ + ۰٫۴ = ۰٫۴۳۷
به همین راحتی گسترده نویسی اعداد اعشاری را انجام دادیم.
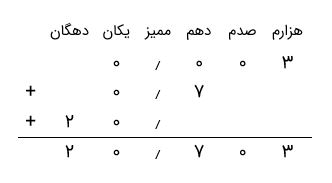
بیایید یک مثال دیگر را بررسی کنیم. فرض کنید عدد اعشاری ۲۰٫۷۰۳ را داریم. میخواهیم این عدد را بهشکل گسترده بنویسیم. اگر گام به گام پیش برویم، بهسادگی این مثال را نیز حل خواهیم کرد.
قبل از هر چیز، جدول ارزش مکانی را تشکیل میدهیم.
| هزارم | صدم | دهم | یکان | دهگان |
| ۳ | ۰ | ۷ | ۰ | ۲ |
اکنون رقم هر مکان را در ارزش آن ضرب میکنیم:
- مکان هزارم: ۳ تا یکهزارم = ۰٫۰۰۱ × ۳ = ۰٫۰۰۳
- مکان صدم: ۰ تا یکصدم = ۰٫۰۱ × ۰ = ۰
- مکان دهم: ۷ تا یکدهم = ۰٫۱ × ۷ = ۰٫۷
- مکان یکان: ۰ تا یکی = ۱ × ۰ = ۰
- مکان دهگان: ۲ تا دهتایی = ۱۰ × ۲ = ۲۰
اکنون برای گسترده نویسی عدد اعشاری کافی است اعدادی را که به دست آوردهایم، با هم جمع کنیم:
۰٫۰۰۳ + ۰٫۷ + ۲۰ = ۲۰٫۷۰۳
اگر این اعداد را زیر هم بنویسیم اینگونه خواهند بود:
گسترده نویسی اعداد اعشاری با کسر
یکی از راههای گسترده نویسی اعداد اعشاری، استفاده از کسرها است. البته این کار بسیار ساده است. کافی است بهجای ارقام پس از اعشار که کوچکتر از یک هستند، از کسر استفاده کنیم. مثلاً بهجای ۰٫۳ میتوان کسر را قرار داد یا بهجای ۰٫۰۰۲ میتوانیم کسر را قرار دهیم.
با بررسی یک مثال، این موضوع روشنتر خواهد شد. فرض کنید میخواهیم عدد اعشاری ۳۴۷۹٫۱۰۵ را به شکل گسترده بنویسیم و از کسرها استفاده کنیم. پیش از هر چیز، برای سادگی میتوانیم جدول زیر را تشکیل دهیم.
| هزارم | صدم | دهم | یکان | دهگان | صدگان | هزارگان |
| ۵ | ۰ | ۱ | ۹ | ۷ | ۴ | ۳ |
در واقع، این عدد را میتوان اینگونه نوشت:
۵ تا یکهزارم + ۰ تا یکصدم + ۱ تا یکدهم + ۹ تا یکی + ۷ تا دهتایی + ۴ تا صدتایی + ۳ تا هزارتایی = ۳۴۷۹٫۱۰۵
یا بهصورت عددی:
۰٫۰۰۱ × ۵ + ۰٫۰۱ × ۰ + ۰٫۱ × ۱ + ۱ × ۹ + ۱۰ × ۷ + ۱۰۰ × ۴ + ۱۰۰۰ × ۳ = ۳۴۷۹٫۱۰۵
۰٫۰۰۵ + ۰ + ۰٫۱ + ۹ + ۷۰ + ۴۰۰ + ۳۰۰۰ = ۳۴۷۹٫۱۰۵
برای اینکه عبارت بالا را بهصورت کسری بنویسیم، کافی است بهجای اعشارها اعداد کسری قرار دهیم. در این صورت، خواهیم داشت:
مثالهای گسترده نویسی اعداد اعشاری
در این بخش، مثالهایی را از گسترده نویسی اعداد اعشاری بررسی میکنیم.
مثال اول
عدد ۹۰۱٫۱۲۸ را بهشکل گسترده بنویسید.
جواب: ابتدا جدول ارزش مکانی ارقام را تشکیل میدهیم.
| هزارم | صدم | دهم | یکان | دهگان | صدگان |
| ۸ | ۲ | ۱ | ۱ | ۰ | ۹ |
طبق جدول این موارد را داریم:
- ۹ تا صدتایی = ۱۰۰ × ۹ = ۹۰۰
- ۰ تا دهتایی = ۱۰ × ۰ = ۰
- ۱ تا یکی = ۱ × ۱ = ۱
- ۱ تا یکدهم: ۰٫۱ × ۱ = ۰٫۱
- ۲ تا یکصدم: ۰٫۰۱ × ۲ = ۰٫۰۲
- ۸ تا یکهزارم: ۰٫۰۰۱ × ۸ = ۰٫۰۰۸
بنابراین، گسترده این عدد به شکل زیر خواهد بود:
۰٫۰۰۸ + ۰٫۰۲ + ۰٫۱ + ۱ + ۹۰۰ = ۹۰۱٫۱۲۸
مثال دوم
عدد ۰٫۳۴۵ را بهشکل گسترده کسری بنویسید.
جواب: ابتدا جدول ارزش ارقام را تشکیل میدهیم.
| هزارم | صدم | دهم |
| ۵ | ۴ | ۳ |
طبق جدول بالا، این مقادیر را داریم:
- ۳ تا یکدهم: ۰٫۱ × ۳ = ۰٫۳
- ۴ تا یکصدم: ۰٫۰۱ × ۴ = ۰٫۰۴
- ۵ تا یکهزارم: ۰٫۰۰۱ × ۵ = ۰٫۰۰۵
در نتیجه، گسترده این عدد بهشکل زیر خواهد بود:
۰٫۰۰۵ + ۰٫۰۴ + ۰٫۳ = ۰٫۳۴۵
با توجه به اینکه، ، و ، شکل گسترده کسری اینگونه خواهد بود:
مثال سوم
شکل گسترده ۰٫۰۰۴ + ۰٫۰۳ + ۲ مربوط به چه عددی است؟
جواب: میبینیم که هزارم، صدم و یکان داریم. استفاده از جدول ارزش مکانی ارقام در این مورد به ما کمک میکند.
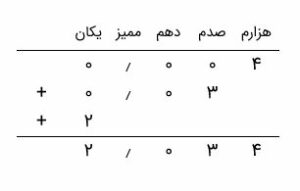
میبینیم که عدد اعشاری مورد نظر ۲٫۰۳۴ است.
تمرینهای گسترده نویسی اعداد اعشاری
در این بخش، چند تمرین را همراه با پاسخ تشریحی ارائه میکنیم که بهتر است برای یادگیری بیشتر، خودتان آنها را حل کنید.
تمرین اول
تمرین دوم
تمرین سوم
جمعبندی
در این آموزش، با گستردهنویسی اعداد صحیح آشنا شدیم. سپس، اعداد اعشاری را مرور کردیم و روش گسترده نویسی اعداد اعشاری را بیان کردیم. در نهایت، به حل چند مثال و تمرین پرداختیم.












