کاربرد جبر خطی در مسائل مهندسی – درونیابی خطی و کاربردهای دیگر
ریاضیات نقش بسیار مهمی در مسائل مرتبط با رشتههای مهندسی از قبیل برق، مکانیک، عمران و غیره دارد. یکی از پرکاربردترین شاخههای ریاضیات در مسائل مهندسی، جبر است. در این مقاله، نحوه انجام برخی از عملیاتهای جبری ساده و متداول در مهندسی از جمله درونیابی خطی، نرمالسازی و تخمین نمودارهای نمایی را برای شما ارائه خواهیم کرد.
درونیابی خطی
«درونیابی خطی» (Linear Interpolation)، فرآیندی است که برای تعیین مختصات یک نقطه مجهول بر روی خط واصل دو نقطه معلوم قرار مورد استفاده قرار میگیرد. در مواقعی که یک مجموعه داده در اختیار داشته باشیم و بخواهیم مقادیر بین دادههای خود را تخمین بزنیم، میتوانیم از روش درونیابی خطی استفاده کنیم.
شکل زیر را در نظر بگیرید. در این شکل، دو نقطه (آبی) با مختصات معلوم (x0,y0) و (x1,y1) و یک نقطه (قرمز) با مختصات مجهول (x,y) نشان داده شده است. در ادامه، مختصات نقطه قرمز را با استفاده از فرآیند درونیابی خطی تعیین میکنیم.
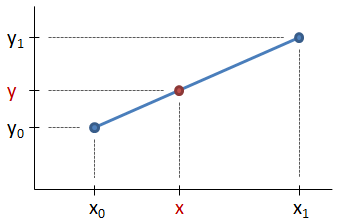
از آنجایی که شیب خط از (x0, y0) تا (x, y) با شیب خط از (x, y) تا (x1, y1) برابر است، خواهیم داشت:
با حل رابطه بالا نسبت به y، معادله درونیابی به دست خواهد آمد:
روشی دیگر برای انجام درونیابی خطی
برای به دست آوردن معادله درونیابی، یک روش دیگر نیز وجود دارد. در این روش، باید بدانید که فاصله x از دو نقطه x0 و x1 با فاصله y از y0 و y1 متناسب است. به عنوان مثال، در صورتی که x در 25 درصد از فاصله x0 تا x1 قرار گرفته باشد، y نیز در 25 درصد از فاصله y0 تا y1 قرار خواهد داشت.
بنابراین، اگر معادله درونیابی را به خاطر نداشته باشید، میتوانید از فرآیند زیر برای درونیابی دو نقطه استفاده کنید:
- در ابتدا باید، نسبت x بین دو نقطه x0 و x1 را به دست بیاورید:
- به خاطر داشته باشید که py (نسبت y بین دو نقطه y0 و y1) با px برابر است:
- رابطه نسبت y بین دو نقطه y0 و y1 را بنویسید و آن را با توجه به پارامتر y حل کنید:
با انجام فرآیند بالا، در نهایت به معادله درونیابی خواهید رسید.
نرمالسازی یک مجموعه داده
«نرمالسازی» (Normalization)، فرآیندی است که برای مقیاسبندی مجموعهای از دادهها صورت میگیرد.
در این فرآیند، باید حاصل جمع تمام دادههای خروجی (پس از نرمالسازی) برابر با 1 شود. به منظور نرمالسازی دادهها، از رابطه زیر استفاده میشود:
ni: مقدار نرمال شده عبارت i ام در مجموعه دادهها؛ vi: مقدار i ام؛ v∑: حاصل جمع تمام مقادیر موجود در مجموعه دادهها
یکی از کاربردهای نرمالسازی، مقایسه چندین داده با مقیاس متفاوت است (مانند مقایسه یک مجموعه داده بسیار بزرگ با یک مجموعه داده بسیار کوچک). در این وضعیت، نرمالسازی برای حذف تأثیر مقیاسهای متفاوت به کار گرفته میشود.
باید توجه داشت که نرمالسازی یک مجموعه داده با نرمالسازی یک بردار مشابه است اما یک تفاوت مهم بین آنها وجود دارد. در نرمالسازی بردار، هر مؤلفه به جای تقسیم بر مجموع مؤلفهها، بر مقدار بردار تقسیم میشود.
تعیین یک معادله نمایی با استفاده از دو نقطه مشخص
بسیاری از پدیدههای مهندسی را میتوان توسط یک منحنی نمایی توصیف کرد. در اغلب موارد، مختصات دو نقطه از این منحنی مشخص است و از این دو نقطه برای تعیین معادله منحنی استفاده میشود. به عنوان مثال، بخش پلاستیک منحنی تنش-کرنش را میتوان به وسیله یک منحنی نمایی تخمین زد. در این شرایط، معمولاً دو نقطه تسلیم و شکست معلوم هستند. با داشتن مقادیر این دو نقطه، امکان تخمین یک معادله برای منحنی تنش-کرنش فراهم میشود. این موضوع، در تخمین منحنی S-N برای طول عمر خستگی نیز صادق است.
در شکل زیر، نمونهای از منحنی تنش-کرنش برای فلز مونل K500 (آلیاژ نیکل و مس) نشان داده شده است. اگر تنها دو نقطه مربوط به مقاومت تسلیم و مقاومت نهایی را داشته باشیم، میتوانیم منحنی تنش-کرنش این ماده را به طور کامل رسم کنیم.

فرم کلی یک معادله نمایی به صورت زیر است:
a: ثابت عددی؛ k: ثابت عددی
اگر دو نقطه از این منحنی نمایی معلوم باشد، ثابتهای بالا با استفاده از روابط زیر قابل محاسبه خواهند بود:
در معادله بالا، (x1, y1) و (x2, y2)، مختصات دو نقطه معلوم هستند. باید توجه داشت که معادلات نمایی در هنگام تبدیل به شکل لگاریتمی، به صورت خطی درمیآیند. بنابراین، در صورت رسم یک منحنی نمایی بر روی نمودار لاگ-لاگ، منحنی به صورت یک خط راست خواهد بود. با استفاده از خواص لگاریتم میتوان معادله نمایی را به صورت لگاریتمی بازنویسی کرد. برای این کار، در ابتدا فرم کلی معادله نمایی را در نظر بگیرید:
پس از تبدیل این معادله به فرم لگاریتمی، رابطه زیر به دست میآید:
در یک نمودار لگاریتمی، معادله لگاریتمی بالا برابر است با:
که در آن:
در معادلات بالا، مقادیر k و a مجهول هستند. برای تعیین k، میتوان شیب منحنی لگاریتمی را محاسبه کرد. در یک معادله خطی، شیب منحنی از رابطه زیر به دست میآید:
که معادل آن در معادله لگاریتمی به صورت زیر است:
با محاسبه عرض از مبدأ منحنی لگاریتمی در یک نقطه معلوم میتوانیم مقدار ثابت a را نیز تعیین کنیم. در یک معادله خطی داریم:
عرض از مبدأ این معادله در نقطه معلوم (x1, y1) به صورت زیر خواهد بود:
به همین ترتیب، عرض از مبدأ منحنی لگاریتمی به صورت زیر قابل محاسبه است:
توجه داشته باشید که پس از تعیین مقدار ثابت k، امکان محاسبه مستقیم ثابت a با استفاده معادله نمایی وجود دارد. برای این کار، تنها باید مقادیر نقطه معلوم (x1, y1) در رابطه زیر جایگذاری کنید:
اکنون، با به دست آوردن ثابتها از طریق دو نقطه معلوم روی منحنی، معادله نمایی مورد نظر مشخص میشود.
امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به مطالعه موضوعات مشابه علاقهمند هستید، مطالب زیر را به شما پیشنهاد میکنیم:
- تعریف های ابتدایی جبر – به زبان ساده
- مجموعه آموزش های مهندسی عمران
- مجموعه آموزشهای دروس مهندسی مکانیک
- مفهوم تنش و کرنش — آشنایی با مفاهیم مقاومت مصالح
- مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد
^^












