مدول برشی چیست؟

در علم مواد، «مدول برشی» (Shear Modulus) یا «مدول صلبیت» (Modulus of Rigidity)، بیانگر نسبت تنش برشی به کرنش برشی است. محاسبه مدول برشی با استفاده رابطه زیر صورت میگیرد. این پارامتر اغلب با حرف «G» و گاهی اوقات با «S» یا «μ» نمایش داده میشود.

τxy: تنش برشی (τxy=F/A)؛ F: نیروی اعمال شده؛ γxy: کرنش برشی (Δx/l=tanΘ)؛ Δx: جابجایی عرضی؛ l: طول اولیه
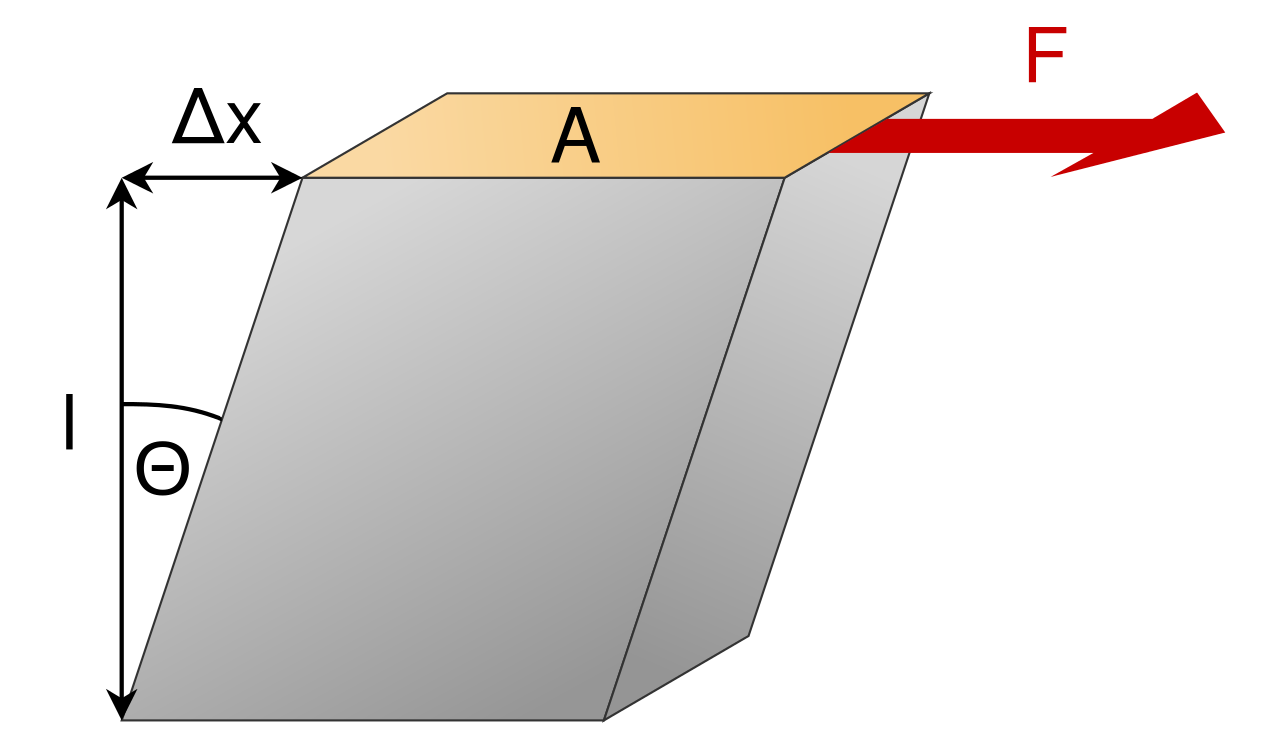
واحد مدول برشی در سیستم SI، پاسکال (Pa) است و معمولاً به صورت گیگا پاسکال (GPa) یا کیلو پوند بر اینچ (ksi) بیان میشود. فرم ابعادی واحد مدول برشی را میتوان به صورت M1L-1T-2 نشان داد (نیرو با جرم ضربدر شتاب جایگذاری میشود).
کاربرد مدول برشی
مدول برشی، یکی از کمیتهای مورد نیاز برای تعیین سختی مواد مختلف است. به منظور محاسبه سختی، قانون کلی هوک برای مقاومت مصالح استفاده میشود که در آن پارامترهای زیر مورد نیاز هستند:
- مدول یانگ (E): این پارامتر، نحوه تغییرات کرنش در راستای تنش تکمحوره وارد شده بر جسم را بیان میکند. کشیدن دو سر یک سیم یا گذاشتن وزنه بر روی یک استوانه را در نظر بگیرید. در این مثالها، نحوه و میزان افزایش طول سیم یا کاهش ارتفاع استوانه، به مدول یانگ مواد بستگی دارد.
- نسبت پواسون (ν): نحوه تغییرات ماده در جهت عمود بر راستای تنش تکمحوره، به وسیله نسبت پواسون نمایش داده میشود. در واقع نسبت پواسون، معیاری برای درک بهتر میزان نازکتر شدن سیم و ضخیمتر شدن استوانه در مثالهای بالا است.
- مدول حجمی (K): این پارامتر، بیانگر تغییرات (یکنواخت) ماده در اثر اعمال فشار هیدرو استاتیک (مانند فشار کف اقیانوس یا یک استخر عمیق) است.
- مدول برشی (G): تغییرات ماده در برابر اعمال تنش برشی، به وسیله مدول برشی نمایش داده میشود. به عنوان مثال، نحوه رفتار یک ماده در برابر برش توسط قیچی را میتوان به وسیله مدول برشی آن پیشبینی کرد.
مدولهای بالا، مستقل نیستند و در مواد همسانگرد، معادله زیر رابطه آنها با یکدیگر است:

جدول زیر، مدول برشی برخی از مواد پر کاربرد در علوم مهندسی را نشان می دهد.
| ماده | مقادیر معمول مدول برشی (بر حسب گیگا پاسکال) در دمای اتاق |
| الماس | 478 |
| فولاد | 79.3 |
| مس | 44.7 |
| تیتانیوم | 41.4 |
| شیشه | 26.2 |
| آلومینیوم | 25.5 |
| آهن | 52.5 |
| پلیاتیلن | 0.117 |
| لاستیک | 0.0006 |
مدول برشی زمانی مورد توجه قرار میگیرد که اعمال دو نیروی موازی و مخالف بر دو طرف سطوح یک جسم صلب، منجر به تغییر شکل آن شود. در صورتی که شکل جسم مورد نظر مکعب باشد، پس از اعمال نیروی برشی، به یک متوازیالسطوح تبدیل خواهد شد. مواد ناهمسانگردی نظیر چوب، کاغذ و اساساً تمام تک بلورها، بر اثر اعمال نیرو در جهات مختلف از خود رفتار متفاوتی را بروز میدهند. در مواجه با این مواد باید از تانسور ثابتهای الاستیک به جای یک مقدار اسکالر استفاده شود.
مفهوم مدول برشی در تعریف سیالات نیز به کار برده میشود. بر اساس این تعریف، سیال مادهای است که مدول برشی آن صفر باشد.
امواج برشی
امواج موجود در اجسام همسانگرد و همگن، به دو نوع «امواج فشاری» (Pressure Waves) و «امواج برشی» (Shear Waves) تقسیم میشوند. سرعت موج برشی (vs) بر اساس مدول برشی جسم و طبق رابطه زیر تعیین میشود:

G: مدول برشی؛ ρ: چگالی جسم
مدول برشی فلزات
مدول برشی فلزات معمولاً با افزایش دما کاهش مییابد. در مقادیر بالای فشار نیز مدول برشی با اعمال فشار کاهش مییابد. در بسیاری از فلزات، بین دمای ذوب، «انرژی تشکیل تهی جای» (Vacancy Formation Energy) و مدول برشی همبستگی وجود دارد. مدلهای مختلفی برای پیشبینی مقدار مدول برشی فلزات و آلیاژها ارائه شده است. مدلهای زیر برای محاسبات «جریان پلاستیک» (Plastic Flow) مورد استفاده قرار گرفتهاند:
- مدول برشی «تنش آستانه مکانیکی» (Mechanical Threshold Stress) یا «MTS»: این مدل توسط «وارشنی» (Varshni) توسعه یافت و در ترکیب با مدل تنش جریان پلاستیک MTS مورد استفاده قرار گرفت.
- مدول برشی «استاینبرگ-کوکران-گنن» (Steinberg-Cochran-Guinan) یا «SCG»: این مدل توسط استاینبرگ و گنن توسعه یافت و در ترکیب با مدل تنش جریان «استاینبرگ-کوکران-گنن-لاند» (Steinberg-Cochran-Guinan-Lund) مورد استفاده قرار گرفته است.
- مدول برشی «نادال و لِپواک» (Nadal and LePoac) یا «NL»: این مدل از «تئوری لیندمان» (Lindemann Theory) برای تعیین وابستگی دما و از مدل SCG برای تعیین وابستگی فشار در مدل برشی استفاده میکند.
مدل MTS
مدل مدول برشی MTS به صورت زیر است:

μ0: مدول برشی در T=0 K؛ K: واحد دمای کلوین؛ D و T0: ثابتهای ماده
مدل SCG
مدل مدول برشی SCG به میزان فشار وابسته بوده و دارای رابطه زیر است:
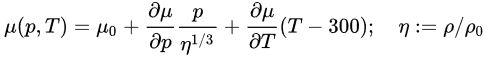
μ0: مدول برشی در وضعیت مرجع (T=300 K, p=0, η=1)؛ p: فشار؛ T: دما
مدل NP
مدل مدول برشی NP، نسخه اصلاح شده مدل SCG است. در مدل NP، وابستگی تجربی دما در مدل SCG با معادلهای بر اساس تئوری لیندمان جایگذاری شده است. معادله مدل NP به صورت زیر است:
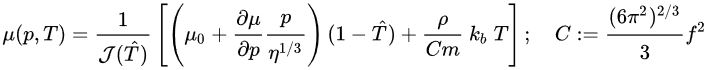
که در آن
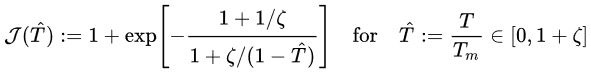
μ0: مدول برشی در 0K و فشار محیط؛ ζ: پارامتر ماده؛ kb: ثابت «بولتزمن» (Boltzmann)؛ m: جرم اتمی؛ f: ثابت لیندمان
امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به مطالعه موضوعات مشابه علاقهمند هستید، مطالب زیر را به شما پیشنهاد میکنیم:
- مجموعه آموزش های مهندسی عمران
- آموزش مقاومت مصالح
- مجموعه آموزشهای دروس مهندسی مکانیک
- آموزش تنش و کرنش بارگذاری محوری در مقاومت مصالح
- مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد
^^












