فرمول حجم کره چیست؟ – به زبان ساده + مثال
حجم کره فضایی است که یک کره اشغال میکند و فرمول محاسبه آن برای کرهای با شعاع برابر است با . در این مطلب از مجله فرادرس یاد میگیریم که فرمول حجم کره چیست و چگونه میتوان حجم یک کره را پیدا کرد. همچنین نحوه استفاده از این فرمول را با حل و بررسی سوالات مرتبط توضیح میدهیم.
- خواهید آموخت که چگونه حجم یک کره را بر حسب قطر آن محاسبه کنید.
- با روش به دست آوردن فرمول حجم کره بر اساس حجم استوانه و مخروط آشنا خواهید شد.
- تفاوتهای کره توخالی و کره توپر را خواهید شناخت.
- با حل سوالات متنوع کاربرد فرمولهای حجم کره را تمرین خواهید کرد.

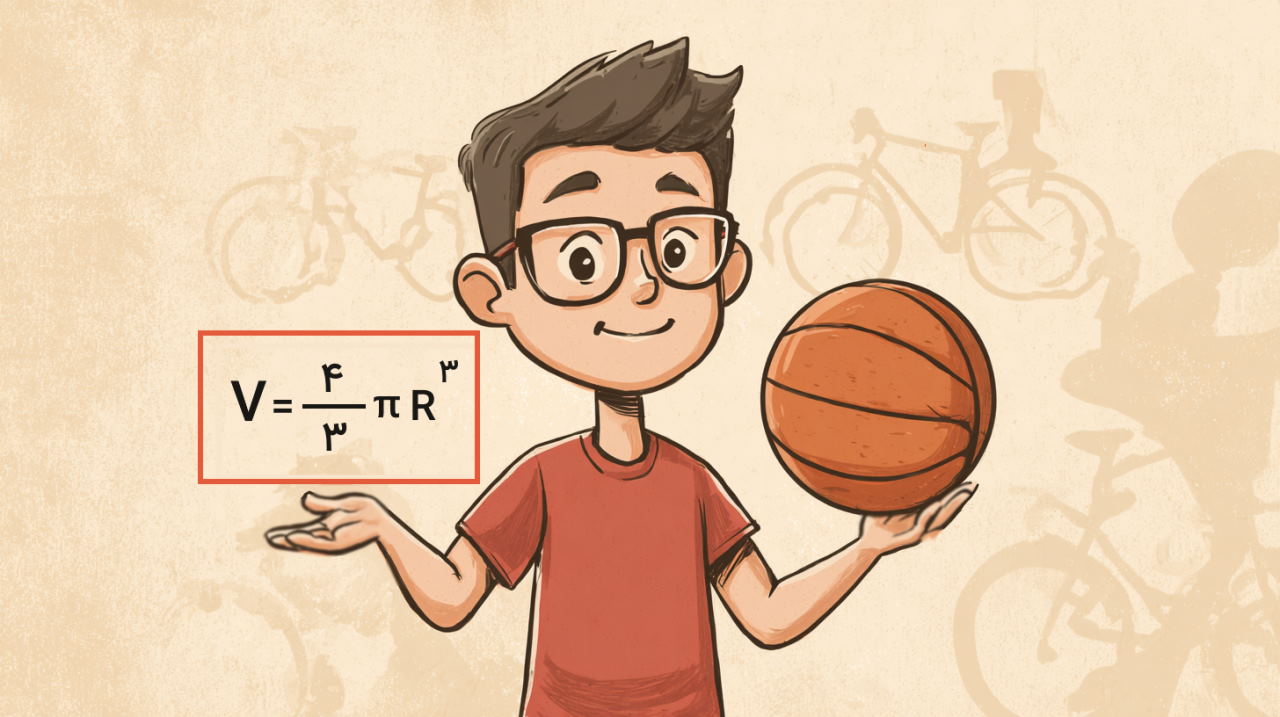
فرمول حجم کره چیست؟
حجم هر کره معادل است با فضایی که آن کره اشغال میکند. حجم یک کره توپر با شعاع توسط رابطه به دست میآید:
= فرمول حجم کرهای با شعاع
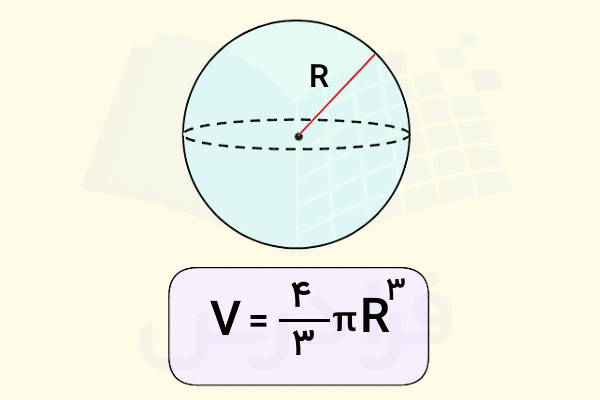
حجم را معمولا با حرف انگلیسی (ابتدای کلمه Volume) نشان میدهند. پس میتوانیم فرمول بالا را به شکل هم بنویسیم. مراحل محاسبه حجم یک کره توپر به شکل زیر است:
- مرحله ۱: اندازه شعاع کره یا را مشخص کنید.
- مرحله ۲: شعاع را به توان سه برسانید یا را محاسبه کنید.
- مرحله ۳: را در ضرب کنید.
- مرحله ۴: مکعب واحد اندازهگیری مناسب را به پاسخ خود اضافه کنید.
حجم کره مقدار فضایی است که یک کره میتواند اشغال کند. واحد حجم کره همیشه برابر است با مکعب یا توان سوم واحد طول بکار رفته برای اندازهگیری شعاع یا قطر کره. برای مثال، اگر شعاع را بر حسب سانتیمتر اندازهگیری کرده باشیم، واحد حجم میشود سانتیمتر مکعب یا . طبق رابطه بالا، فرمول حجم کره کاملا به شعاع آن بستگی دارد و کم یا زیاد شدن شعاع، باعث تغییر در حجم کره میشود.
فرمول حجم کره بر حسب قطر چیست؟
همچنین ممکن است در سوالات مختلف به جای شعاع یک کره، قطر آن را داشته باشیم. با توجه به اینکه همواره قطر کره یا دو برابر شعاع آن است، پس میتوانیم فرمول حجم کره را بر حسب قطر آن به شکل زیر بنویسیم:
بنابراین فرمول حجم کره ای با قطر برابر است با .
یادگیری مساحت و حجم اشکال هندسی با فرادرس
یادگیری مساحت و حجم نیازمند این است که ابتدا با ویژگیهای اشکال هندسی مختلف آشنا شوید. سپس باید بتوانید مفاهیمی مانند محیط و مساحت و حجم را از هم تفکیک کنید. در کتابهای درسی ویژگیهای فرم دو بعدی یک کره، یعنی دایره، برای اولین بار در کتاب ریاضی هشتم مطرح میشود. سپس در کتاب ریاضی نهم مبحث حجم و مساحت کره همراه با روش بهدست آوردن حجم احجامی مانند هرم و مخروط توضیح داده شده است. بنابراین اگر علاقهمند هستید با فرمولهای مربوط به این مباحث همراه با آموزش تصویری و حل مثالهای گسترده آشنا شوید، پیشنهاد میکنیم فیلمهای آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید:
- فیلم آموزش ریاضی پایه هشتم فرادرس
- فیلم آموزش ریاضی پایه نهم فرادرس
- فیلم آموزش ریاضی نهم – نکته و تست آزمون نمونه دولتی و تیزهوشان فرادرس
- فیلم آموزش رایگان محاسبه حجم کره و مساحت رویه فرادرس
- فیلم آموزش رایگان محاسبه مساحت سطح حاصل از دوران فرادرس
- فیلم آموزش رایگان خط و دایره ریاضی (هشتم) + حالتهای مختلف با مثال فرادرس
- فیلم آموزش رایگان محاسبه مساحت دایره و حلقه فرادرس
فرمول حجم کره تو خالی چیست؟
دقت کنید دو نوع کره داریم، کره توپر و کره توخالی که حجم این دو نیز با هم متفاوت است. در کره توپر فقط یک شعاع داریم، اما در کره توخالی دو شعاع وجود دارد. در واقع یک کره توخالی از دو پوسته کروی شکل و هممرکز ساخته شده است که شعاع یکی از دیگری بزرگتر است. به این ترتیب حجم کره توخالی با شعاع داخلی و شعاع خارجی توسط فرمول زیر محاسبه میشود:
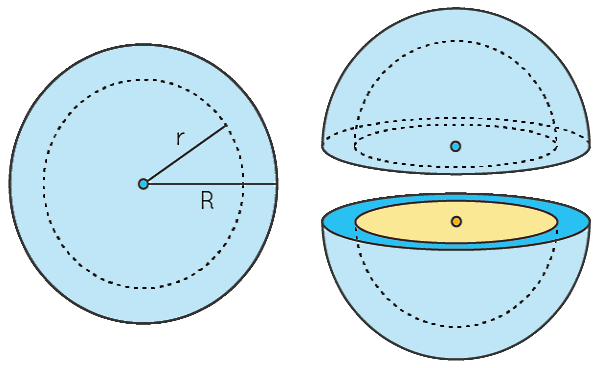
پس میتوانیم بگوییم که فرمول حجم کره به توپر یا توخالی بودن آن نیز بستگی دارد.
در ادامه دقیقتر بررسی شده است که حجم کره توخالی چگونه بهدست میآید:
حجم کره داخلی - حجم کره خارجی = حجم کره توخالی
= حجم کره توخالی
= حجم کره توخالی
فرمول حجم کره چگونه به دست می آید؟
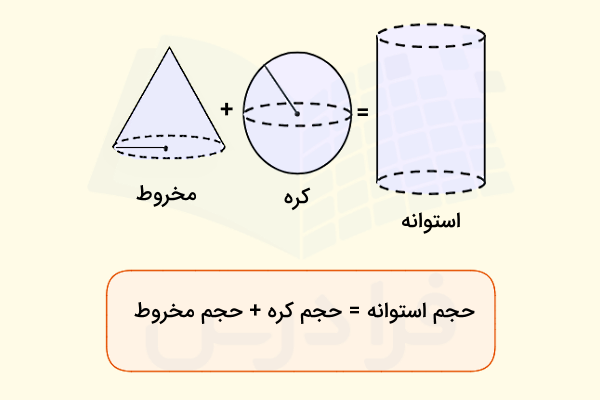
دانشمندی به نام ارشمیدس برای اولین بار متوجه شد که اگر شعاع یک استوانه، مخروط و کره یکسان و برابر با باشد، ارتفاع مخروط و استوانه با قطر کره یا برابر باشد و هر سه این شکلها دارای مقطع عرضی یکسان باشند (یعنی اگر از بالا نگاه کنیم، دایرهای به شعاع برای هر سه شکل دیده شود)، در این صورت نسبت حجم آنها بهصورت زیر خواهد بود:
= کره : مخروط : استوانه
این توضیح نشان میدهد که برای مثال حجم استوانه برابر است با:
حجم استوانه = حجم مخروط + حجم کره
با توجه به این ارتباط میتوانیم فرمول حجم کره را با دانستن فرمول حجم استوانه و حجم مخروط به شکل زیر پیدا کنیم. فقط باید در نظر داشته باشید که فرض کرده بودیم ارتفاع مخروط و استوانه یا برابر است با :
حجم مخروط - حجم استوانه = حجم کره
= حجم استوانه
= حجم مخروط
= حجم کره
ملاحظه میکنید که با این روش میتوان فرمول حجم کره را استنتاج کرد.
محاسبه شعاع کره با داشتن حجم آن
پس از اینکه آموختیم فرمول حجم کره چیست، در این بخش نشان میدهیم اگر حجم کرهای در یک سوال مشخص بود، چگونه میتوانیم شعاع آن کره را محاسبه کنیم. کافی است را در فرمول حجم کره به شکل زیر به دست آوریم:
در بخش بعد مثالی داریم که در آن از این فرمول را پیدا کردن شعاع کره استفاده میشود.
حل مثال از فرمول حجم کره
پس از اینکه با انواع فرمول حجم کره کاملا آشنا شدید، در این بخش با حل سوالات متنوع به شما کمک میکنیم تا به نحوه بهدست آوردن حجم کره کاملا مسلط شوید. ضمن اینکه در همین راستا میتوانید از مطلب «حجم کره و محاسبه آن | به زبان ساده» مجله فرادرس نیز استفاده کنید.
مثال ۱
حجم کرهای با شعاع چند سانتیمتر مکعب است؟
پاسخ
برای محاسبه حجم زمانی که به توپر یا توخالی بودن کره اشاره نشده است، از فرمول حجم کره توپر استفاده میکنیم:
= حجم کره
اما چون پاسخ بر حسب سانتیمتر مکعب خواسته شده است، پس بهتر است پیش از محاسبه حجم ابتدا تبدیل واحد اینچ به سانتیمتر را انجام دهیم:
مثال ۲
مقدار هوایی که در توپی با قطر ذخیره میشود، چقدر است؟
پاسخ
میدانیم هوای داخل یک توپ کروی شکل یا هر جسم سه بعدی بستهای معادل است با حجم آن شکل. بنابراین کافی است حجم توپ کروی شکلی با قطر را پیدا کنیم:
مثال ۳
مینا سه تیله کروی شکل با شعاعهای و و دارد. او تصمیم گرفته است تا هر سه تیله را به کمک پدرش ذوب کند و با ماده به دست آمده یک تیله واحد بسازد. آیا میتوانید شعاع تیله جدید را حدس بزنید؟
پاسخ
فرض کنید شعاع این سه تیله کوچک را به ترتیب از کمترین تا بیشترین به صورت و و و شعاع تیله جدید را نامگذاری کنیم. با توجه به اینکه با ذوب شدن سه تیله کوچک تیله جدید ساخته میشود، پس رابطه زیر بین حجم این تیلهها برقرار است:
حجم تیله سوم + حجم تیله دوم + حجم تیله اول = حجم تیله جدید
با فاکتورگیری عبارت از تمام جملات سمت راست در عبارت بالا و ساده کردن آن از طرفین تساوی خواهیم داشت:
حالا با قرار دادن مقادیر شعاع مقدار تعیین میشود:
مثال ۴
اگر حجم کرهای باشد، شعاع آن چقدر است؟
پاسخ
برای پیدا کردن شعاع کره با داشتن حجم آن کافی است از فرمول زیر استفاده کنیم:
مثال ۵
حجم یک کره توخالی با شعاع داخلی و شعاع خارجی را بهدست آورید:
پاسخ
گفتیم فرمول حجم یک کره توخالی به شکل زیر است:
پس با جایگزینی مقادیر شعاع، خواهیم داشت:
کره چیست و چگونه تشکیل می شود؟
کره یک شکل سه بعدی است که هیچ لبه یا راسی ندارد و تمام نقاط روی سطح آن از مرکز فاصله یکسانی دارند. به عبارت دیگر، فاصله مرکز کره تا هر نقطه روی سطح آن همواره برابر با عدد یکسانی است. به همین دلیل تعریف کره در ریاضیات به این صورت است: مکان هندسی نقاطی که همگی در فاصلهای مساوی از یک نقطه مشترک در فضای سهبعدی قرار دارند.
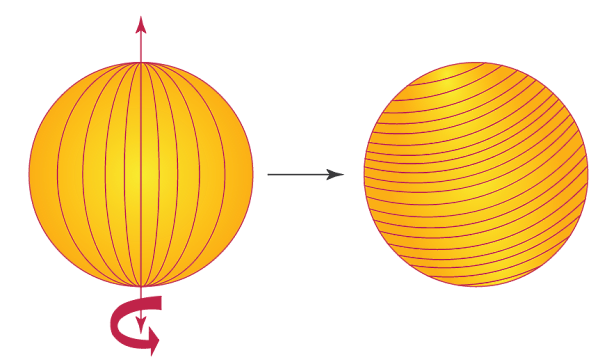
برای تشکیل یک کره کافی است روی برگهای یک دایره رسم کنیم، آن را برش دهیم، یک نخ را در امتداد قطر آن بچسبانیم و سپس دایره بریده شده را حول این نخ بچرخانیم، شکل بهدست آمده یک کره است.
ویژگی های کره
گفتیم کره یک شکل سه بعدی است که تمام نقاط روی سطح بیرونی آن در فاصله یکسانی از مرکز قرار دارند. ویژگیهای زیر به شناسایی شکل کره کمک میکنند:
- یک کره در تمام جهات متقارن است.
- دارای سطح منحنی است.
- هیچ لبه یا راسی ندارد.
- هر نقطه روی سطح کره در فاصلهای ثابت از مرکز آن قرار دارد که این فاصله همان شعاع کره است.
- کره یک چند وجهی (Polyhedron) نیست، چون چند وجهی باید دارای وجههای مسطح، لبهها و راسها باشد.
- بین تمام شکلهایی که سطحی برابر دارند، کره بیشترین حجم را خواهد داشت.
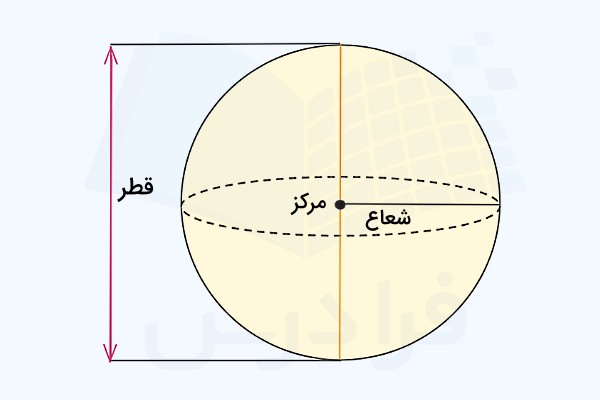
همچنین مهمترین پارامترهای ریاضیاتی که برای یک کره تعریف میشوند عبارتاند از:
- شعاع کره: طول پارهخطی است که از مرکز کره تا هر نقطه روی سطح آن رسم میشود.
- قطر کره: طول پارهخطی است که از یک نقطه روی سطح کره به نقطه مقابل آن روی سطح متصل میشود، در حالی که از مرکز نیز عبور میکند. قطر کره دقیقا دو برابر شعاع آن است.
- محیط کره: طول یا دور بزرگترین دایرهای که در یک کره وجود دارد، معادل محیط آن کره است. در تصویر بالا، مرز دایره نقطهچین یا مقطعی از کره که شامل مرکز آن است، به عنوان محیط شناخته میشود.
- مساحت کره: معادل مساحتی است که سطح یک کره اشغال میکند.
- حجم کره: مقدار فضای اشغال شده توسط یک کره است.
فرمول محیط و مساحت کره
در محاسبات یک کره لازم است به تفاوت فرمولهای محیط، مساحت و حجم آن دقت کنیم:
| فرمول محیط کرهای با شعاع | |
| فرمول مساحت کرهای با شعاع | |
| فرمول مساحت کرهای با قطر |
نیم کره
در هندسه نیمکره به هر شکل سه بعدی گفته میشود که از برش یک کره به دو قسمت مساوی حاصل شده است. سطح افقی و هموار نیمکره قاعده یا وجه نام دارد و سطح دیگر آن به شکل یک کاسه دایرهای شکل است. نیمکره زمانی تشکیل میشود که یک کره از مرکز و در امتداد قطر خود برش داده شود. با توجه به اینکه نیمکره دقیقا نصف کره است، پس فرمول حجم آن نیز از نصف کردن فرمول حجم کره حاصل میشود:
= فرمول حجم نیمکرهای با شعاع
آزمون حجم کره
در انتهای این مطلب از مجله فرادرس میتوانید با پاسخدهی به سوالات آزمون زیر میزان تسلط خود را بر مباحث و فرمولهای بیان شده متوجه شوید. نمره نهایی شما نیز با کلیک روی گزینه «مشاهده نتایج آزمون» قابل مشاهده است. همچنین برای حل سوالات متنوعتر در این زمینه و با نگاهی به آزمونهای ورودی دبیرستانهای نمونه دولتی یا تیزهوشان، فرادرس یک فیلم آموزشی با عنوان فیلم آموزش ریاضی نهم - نکته و تست آزمون نمونه دولتی و تیزهوشان تهیه کرده است که جهت دسترسی آسانتر، لینک آن نیز در ادامه برای شما قرار داده شده است:
تمرین و آزمون
حجم نیمکره زیر کدام است؟
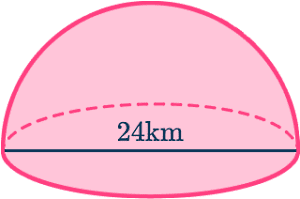
گزینه سوم صحیح است. حجم یک نیمکره نصف حجم کره است. در این سوال چون قطر کره داده شده است، فرمول حجم کره کامل برابر است با . در نتیجه حجم نیمکره با نصف کردن این عبارت و به شکل زیر محاسبه میشود:
اگر شعاع بیرونی یک کره توخالی دو برابر شعاع داخلی آن باشد، حجم این کره برابر است با:
گزینه سوم درست است. میدانیم فرمول حجم یک کره توخالی به شکل زیر است:
در صورت سوال گفته شده که شعاع خارجی یا دو برابر شعاع داخلی یا است، پس داریم:
حالا با جایگزینی مقادیر شعاع، خواهیم داشت:
یک تانکر آب کروی شکل شعاعی برابر با دارد. این تانکر با چه حجمی از آب کاملا پر میشود؟
گزینه آخر درست است. در این سوال برای پیدا کردن حجم آب لازم است حجم تانکر را پیدا کنیم:
اگر حجم کرهای باشد، قطر آن برابر با کدام گزینه است؟
گزینه سوم صحیح است. با نوشتن فرمول حجم کره بر حسب قطر آن به شکل زیر خواهیم داشت:
حجم نیمکرهای با شعاع برابر با کدام گزینه است؟
هیچکدام
اگر شعاع کرهای دو برابر شود، حجم آن چقدر تغییر خواهد کرد؟
هشت برابر بیشتر میشود.
شش برابر بیشتر میشود.
چهار برابر بیشتر میشود.
نه برابر بیشتر میشود.
اگر شعاع یک نیمکره باشد، حجم کره حاصل چقدر است؟
اگر حجم کرهای سه برابر شود، نسبت شعاع اولیه به شعاع نهایی آن برابر است با:
گزینه اول و دوم هر دو صحیح هستند.
اگر شعاع کرهای باشد، نسبت مساحت به حجم آن برابر با کدام گزینه است؟
حجم یک کره توخالی با شعاع داخلی و شعاع خارجی چند سانتیمتر مکعب است؟












