دی الکتریک — به زبان ساده

در این مقاله قصد داریم تا با زبانی ساده به بررسی و مفهوم دی الکتریک و تاثیر آن بر ظرفیت خازن بپردازیم. دی الکتریکها، مواد عایقی (نارسانای الکتریکی) هستند که در صورت اعمال میدان الکتریکی، قطبی میشوند. البته موادی دی الکتریک که ذاتاً قطبی باشند نیز وجود دارند. اگر علاقهمند به یادگیری این موضوع هستید، با ما در ادامه این مطلب همراه باشید.
قطبی شدگی
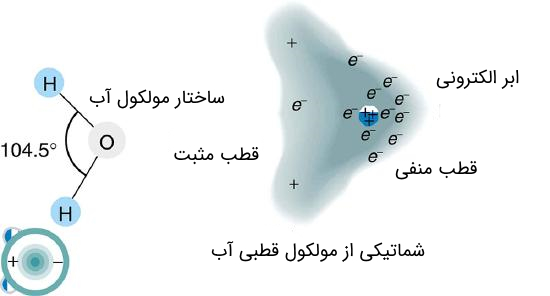
در حالت کلی میتوان مولکولها را در دو حالت قطبی و غیرقطبی تقسیم بندی کرد. در اینجا واژه «قطب» به حالت بارهای الکتریکی اشاره دارد. در مولکولهای قطبی به صورت ذاتی یک جدایی بار وجود دارد که در مولکولهای ناقطبی چنین چیزی مشاهده نمیشود. در واقع مولکولهای قطبی نظیر آب، به صورت دائم حاوی دوقطبیهای الکتریکی بوده و مولکولهای ناقطبی مثل اکسیژن فاقد دوقطبیهای الکتریکی هستند.
البته مولکولهای ناقطبی در حضور یک میدان الکتریکی خارجی میتوانند قطبی شوند که به این حالت، قطبش القایی میگویند. برای درک شهودی بهتر در خصوص قطبش القایی، به شکل زیر دقت کنید.
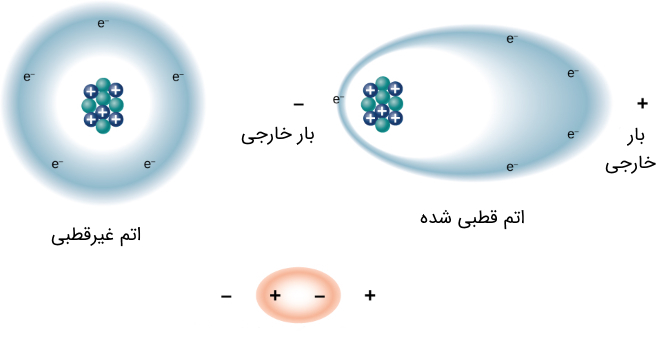
مفهوم قطبش در بحث دی الکتریک به این صورت است که مطابق شکل فوق، در یک اتم ناقطبیده، توزیع الکترونها به صورت یکنواخت در اطراف هسته است. اما در یک اتم قطبی توزیع الکترونها یکنواخت نبوده و در قسمتی از اتم جمعیت الکترونها بیشتر است. در این حالت میتوان آن سمت که حاوی الکترونهای بیشتر است را در مقابل بار مثبت هسته، قطب منفی به شمار آورد. با اعمال یک میدان الکتریکی میتوان توزیع الکترونها را به سمت تشکیل قطب منفی تغییر داد. در این صورت مولکول ناقطبی در حضور میدان الکتریکی تبدیل به مولکول قطبی میشود.
میدان الکتریکی دوقطبی
در مقاله «میدان الکتریکی (Electric Field) چیست؟ — از صفر تا صد» با مفهوم و نحوه به دست آوردن میدان الکتریکی آشنا شدید.
در اینجا قصد داریم، میدان الکتریکی حاصل از یک دوقطبی (یک بار مثبت و یک بار منفی) را در نقطهای در راستای محور دو قطبی مطابق با شکل (3) به دست آوریم.
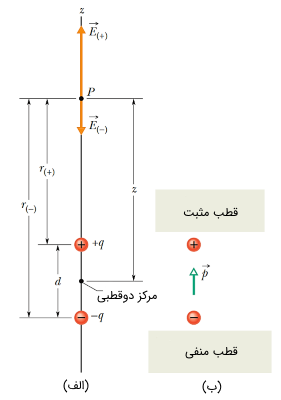
مطابق با شکل (۳) فاصله بین قطب (بار) مثبت و قطب (بار) منفی به اندازه و فاصله نقطهای که در آن میدان محاسبه میشود تا مرکز دوقطبی است. میدان در نقطه عبارت است از:
(1)
طبق شکل (3)، فواصل و را میتوانیم به صورت زیر تعریف کنیم.
(2)
(3)
با جایگذاری در معادله (۱) و فاکتورگیری از نتیجه میشود:
(4)
با استفاده از اتحاد قسمت پرانتزی رابطه فوق را میتوانیم به شکل زیر بنویسیم:
(5)
از آنجایی که معمولاً میدان را در نقطهای دور از دوقطبی به دست میآوریم ()، حاصل شده و لذا از آن صرفنظر میکنیم. در نتیجه:
(6)
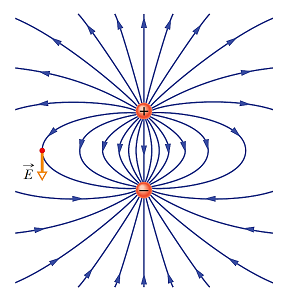
در رابطه فوق به عبارت بردار قطبش گفته شده که آن را با نمایش میدهند. جهت در یک دوقطبی همیشه از بار منفی به سمت بار مثبت است (شکل ۳). شکل (۴) خطوط میدان یک دوقطبی الکتریکی را نشان میدهد.
قطبش دی الکتریک
در این بخش میخواهیم به تاثیر میدان الکتریکی بر دوقطبیها بپردازیم. در حالت اول تصور کنید که یک ماده دی الکتریک قطبی در اختیار داریم. منظورمان وجود دوقطبیهای الکتریکی در ساختار دی الکتریک است. همانطور که در شکل (5) مشاهده میکنید در غیاب میدان الکتریکی، جهتگیری این دوقطبی ها به صورت تصادفی و درهم بوده که در نتیجه میدانهای الکتریکی تولید شده توسط آنها، یکدیگر را خنثی میکند.
با قرار دادن این ماده دی الکتریک در میدان الکتریکی خارجی یکنواخت (مثلاً بین صفحات یک خازن تخت)، جهتگیری دوقطبیها در راستای میدان خارجی شده و لذا تمامی دوقطبیها همتراز میشوند. البته شدت همترازی بستگی به شدت میدان الکتریکی خارجی دارد.
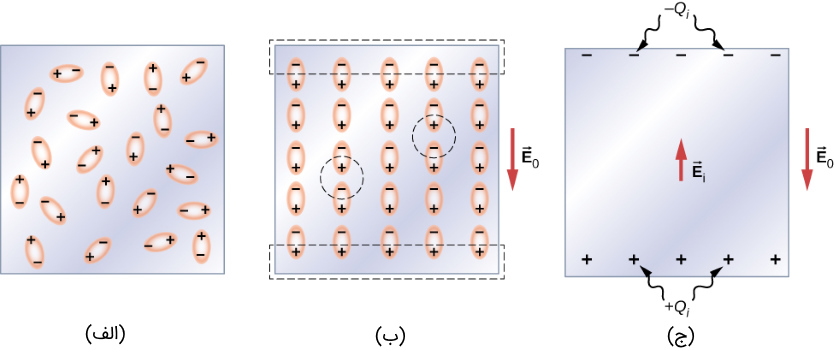
با اعمال میدان الکتریکی خارجی، بارهای مخالف یکدیگر را خنثی کده و لذا هیچ بار خالصی در دیالکتریک وجود ندارد (دایرههای شکل 5-ب). البته مطابق با شکل، این امر در نزدیکی لبههای دیالکتریک، جایی که جمعیت بارهای مثبت و یا منفی زیاد است، صادق نیست. دقت شود که میدان الکتریکی خارجی تنها، دوقطبیها را تراز کرده و ارتباطی به القای بار ندارد. یک دیالکتریک در کل خنثی است و حتی در صورت اعمال میدان الکتریکی خارجی، تعداد بارهای مثبت و منفی که در لبهها حضور مییابند، یکسان است. در شکل (5) مشخص است که بارهای لبه، خود، میدانی در خلاف جهت میدان الکتریکی خارجی ایجاد میکنند.
مطلب فوق در خصوص مواد دی الکتریک غیرقطبی نیز صادق است. در واقع با اعمال یک میدان الکتریکی خارجی با شدت مناسب، میتوانیم باعث جدایی بارهای مثبت و منفی اتمهای (مولکول) ماده دی الکتریک شویم. این جدایی بار به منزله تشکیل دوقطبی در ماده دیالکتریک بوده که این دوقطبیها در همان میدان (عامل تولید) همتراز میشوند و مثل حالت قبل میدانی در خلاف جهت میدان اصلی خارجی ایجاد میکنند. با تفاسیر فوق، میدان الکتریکی، داخل یک دیالکتریک صرف نظر از قطبی یا غیرقطبی بودنش، ضعیف میشود.
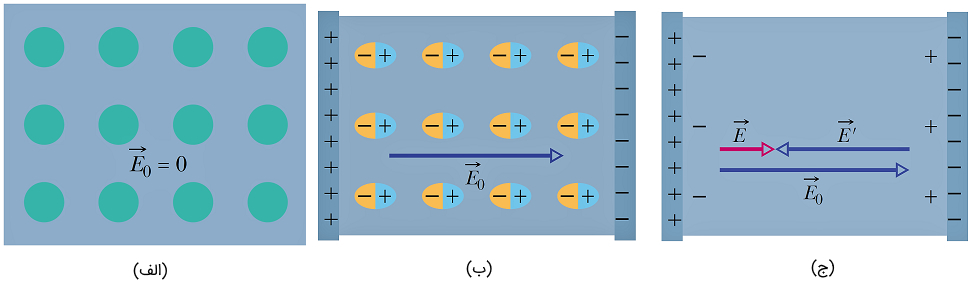
میدان الکتریکی داخل یک دیالکتریک را میتوان به شکل زیر به دست آورد:
(1)
در رابطه فوق، میدان الکتریکی خارجی (میدان یکنواخت بین صفحات خازن) و میدان الکتریکی ناشی از دوقطبیها است. واضح است که میدان فوق، مقداری کمتر از میدان خارجی در غیاب ماده دیالکتریک دارد. برای فرمولبندی مطلب و اینکه درک بهتری از میزان تاثیر دیالکتریک در کاهش میدان خارجی داشته باشیم، نسبت میدان خارجی (غیاب دیالکتریک) به میدان در حضور دیالکتریک را کمیتی با عنوان ثابت دی الکتریک تعریف میکنیم.
(2)
دقت شود، از آنجایی که میدان در حضور دی الکتریک همیشه کوچکتر از میدان خارجی (غیاب دی الکتریک) است، مقدار همیشه بزرگتر از یک است. با استفاده از رابطه فوق، میتوانیم میدان ناشی از دوقطبیها را بر حسب میدان خارجی، به فرم زیر بنویسیم:
(3)
مقاومت دی الکتریک
پیشتر اشاره کردیم که میزان همترازی دوقطبیها بستگی به شدت میدان الکتریکی خارجی دارد. اگر میدان الکتریکی خارجی خیلی قوی باشد، باعث جدایی کامل بارهای مثبت و منفی میشود. در واقع باعث جدا شدن الکترونها از اتمها شده و در نتیجه اتمها یونیزه میشوند.
این الکترونهای جدا شده، مصداق الکترونهای آزادی هستند که میتوانند آزادانه حرکت کرده و در نتیجه بار الکتریکی از طریق دیالکتریک منتقل شود. به این پدیده شکست دی الکتریک میگویند.

حداقل شدت میدان الکتریکی که در آن مولکولها و اتمهای ماده دیالکتریک یونیزه میشوند (مقدار بحرانی میدان الکتریکی) را مقاومت دیالکتریک مینامند. این مقدار بحرانی، محدودیتی برای ولتاژ کاری تجهیزاتی نظیر خازن، که در آنها از دی الکتریک استفاده میشود، اعمال میکند.
به طور مثال، مقاومت دی الکتریک هوا (مقدار بحرانی شدت میدان الکتریکی) برابر است. بنابراین اگر در فضای بین دو صفحه خازن به فاصله ۱ میلیمتر، هوا پر شده باشد، ولتاژ شکست (ولتاژ بحرانی) برابر با مقدار زیر میشود ().
از رابطه فوق پی میبریم که در ولتاژهای زیر مشکلی برای خازن مذکور پیش نمیآید. لازم به ذکر است که بحث ولتاژ شکست برای گازهای مختلف در فیزیک پلاسما از اهمیت زیادی برخوردار است.

ظرفیت خازن با دی الکتریک

در مقاله «ظرفیت خازن -- یادگیری با مثال» با محاسبه ظرفیت خازن پر شده با دی الکتریک توسط «قانون گاوس» (Gauss's law) آشنا شدیم. دیدم که وجود دیالکتریک باعث افزایش ظرفیت خازن میشود. به طور خلاصه، قرار گرفتن یک ماده دی الکتریک در بین صفحات خازن، باعث کاهش میدان الکتریکی اولیه (غیاب دی الکتریک) میشود. اما از آنجایی که خازن به یک ولتاژ ثابتی متصل است، برای اینکه میدان کاهش یافته جبران شود، مقدار بارهای بیشتری روی صفحات خازن جمع میشوند. در نتیجه مطابق با رابطه ظرفیت خازن افزایش پیدا میکند.
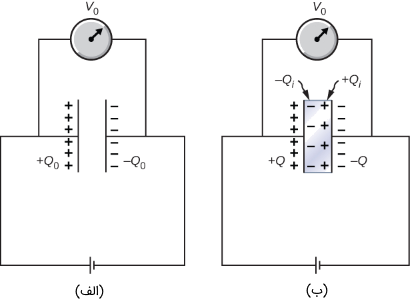
در شکل (۱۰-الف)، خازنی با صفحات تخت (بدون ماده دی الکتریک) به ولتاژ ثابت متوسط شده است. طبق رابطه انتگرالی ولتاژ ()، میدان الکتریکی بین صفحات این خازن به صورت زیر است:
(1)
در این حالت ظرفیت این خازن و بار ذخیره شده روی صفحات آن است. طبق رابطه ظرفیت خازن تخت، میتوانیم ظرفیت یک خازن را به صورت ضریبی از ظرفیت همان خازن بدون دیالکتریک بنویسیم که این ضریب همان ثابت دی الکتریک () است.
(2)
پس در شکل (10-ب)، بار ذخیره شده روی صفحات خازن () در حالتی که با ماده دی الکتریک پر شده است به صورت زیر در میآید:
(3)
ملاحظه میشود که با قرار دادن ماده دی الکتریک بین صفحات یک خازن، ظرفیت آن افزایش پیدا کرده و بار بیشتری بر روی صفحات آن ذخیره میشود. از آنجایی که خازن به ولتاژ ثابت متصل است، میدان بین صفحات باید ثابت باشد. در واقع به همین دلیل بار بیشتری بر روی صفحات جمع میشوند تا کاهش میدان توسط دی الکتریک را جبران کنند. از قانون گاوس نتیجه میگیریم:
(4)
از رابطه فوق نتیجه میشود که مقدار بار حاصل از دوقطبیهای ماده دیالکتریک در خازن () به صورت زیر با بار (غیاب دی الکتریک) رابطه دارد.
(5)
از مطالب فوق نتیجه میشود حداکثر مقدار باری که روی صفحات یک خازن میتواند وجود داشته باشد، بستگی به مقاومت دیالکتریک، یعنی ولتاژ شکست آن دارد. به طور مثال، مقاومت دی الکتریک تفلون حدود است که ولتاژ شکست برای ضخامت ۱ میلیمتر از آن است. از بحث فوق ملاحظه میشود که مقدار بار جمع شده در صفحات خازن پر شده با هوا به صورت است. در حالی که اگر همین خازن را با ماده دی الکتریک تفلون پر کنیم، داریم:
(6)
همانطور که مشاهده میشود، در صورت قرار دادن ماده دی الکتریک تفلون در خازن، حدود 42برابر بار بیشتری در صفحات خازن نسبت به هوا () جمع میشود. البته دقت کنید که در حقیقت ثابت دی الکتریک خلأ برابر با یک بوده و برای هوا با تقریب خوبی همان ۱ در نظر گفته میشود. در زیر جدول ثابت دی الکتریک مواد مختلف به همراه مقاومت دی الکتریک آنها آورده شده است:
| محیط (ماده) | ثابت دی الکتریک () | مقاومت دی الکتریک |
| خلأ | 1 | ∞ |
| هوا (خشک در فشار یک اتمسفر) | 1.00059 | 3.0 |
| تفلون | 2.1 | 60~173 |
| پارافین | 2.3 | 11 |
| روغن سیلیکون | 2.5 | 10~15 |
| پلیاستر | 2.56 | 19.7 |
| نایلون | 3.4 | 14 |
| کاغذ | 3.7 | 16 |
| کوارتز | 3.78 | 8 |
| شیشه | 4~6 | 9.8~13.8 |
| بتن | 4.5 | - |
| بِیک لایت (نوعی پلاستیک) | 4.9 | 24 |
| الماس | 5.5 | 2000 |
| شیشه پیرِکس | 5.6 | 14 |
| میکا (سنگ/شیشه معدنی) | 6.0 | 118 |
| لاستیک نئوپرن | 6.7 | 15.7~26.7 |
| آب | 80 | - |
| اسید سولفوریک | 84~100 | - |
| تیتانیوم دی اکسید | 86~173 | - |
| تیتانایت باریم | 1200~10000 | - |
| کلسیم مس تیتانایت | بیش از 250000 | - |
گذردهی الکتریکی
در مقاله «گذردهی الکتریکی -- به زبان ساده» با بحث گذردهی الکتریکی به طور کامل آشنا شدیم. در این بخش قصد داریم مفهوم گذردهی را با زبانی ساده مطرح کنیم. شاید بتوان گفت مهمترین ویژگی یک دی الکتریک، گذردهی آن باشد. گذرهی () را میتوان میزان قطبشپذیری یک ماده دانست که از حاصل ضرب گذردهی خلأ () در ثابت دی الکتریک () به دست میآید.
(1)
لازم به ذکر است که به ثابت دی الکتریک ()، نفوذپذیری یا گذردهی نسبی () نیز میگویند. چرا که نسبت گذردهی محیط (ماده دیالکتریک) به گذردهی خلأ () تعریف میشود. به بیانی دیگر، گذردهی نسبی یک ماده را میتوان نسبت ظرفیت خازن پر شده با آن ماده به ظرفیت همان خازن، منتها پر شده با هوا (خلأ) تعریف کرد.
(2)
ثابت گذردهی خلأ () از ثابتهای فیزیک به حساب میآید و طبق رابطه زیر به سرعت نور در خلأ و نفوذپذیری مغناطیسی (تراوایی مغناطیسی) در خلأ مربوط میشود. از «قانون کولن» (Coulomb’s law) میتوان نتیجه گرفت که ، واحد بار الکتریکی را به کمیتهای مکانیکی نظیر نیرو و جابهجایی (مکان) مربوط میسازد.
(3)
قطبشپذیری نیز به مفهوم تمایل نسبی توزیع الکترونها به انحراف از شکل عادی خود به واسطه اعمال میدان الکتریکی خارجی است. قطبشپذیری الکترونی را معمولاً با نماد α نشان داده و نسبت بردار قطبش بر میدان الکترونی ایجاد کننده همان بردار قطبش است.
(4)
البته رابطه بردار قطبش با میدان الکتریکی در حالت کلی غیرخطی بوده و مولفههای مرتبه دوم، مرتبه سوم و ... به شکل زیر دارد:
(4)
در رابطه فوق، «پذیرفتاری» یا ضریب حساسیت اکتریکی (Electric susceptibility) است. پرداختن به فیزیک پذیرفتاری الکتریکی خارج از حوصله این مقاله بوده و خود مقاله تخصصیتری را طلب میکند. اما به طور ساده، ثابتی بدون واحد بوده که درجه قطبیشدگی مواد دی الکتریک را در پاسخ به میدان الکتریکی نشان میدهد. تاثیر مستقیمی بر ضریب گذردهی الکتریکی داشته که در نتیجه بر دیگر متغیرها همانند ظرفیت خازنی یا سرعت نور در آن محیط تاثیر میگذارد. این ضریب برای مرتبههای دوم و بالاتر عدد کوچکی بوده و در نتیجه اثرات غیرخطی در میدانهای الکتریکی با شدت بالا نمود پیدا میکنند. برای مرتبه اول (حالت خطی) داریم:
(5)
رابطه با گذردهی نسبی یا ثابت دی الکتریک () به صورت زیر است:
(6)
به هنگام مطالعه میدان الکتریکی یا به طور جامعتر مطالعه معادلات ماکسول در یک محیط، برای سادگی معادلات در بررسی میکروسکوپی مواد، پارامتر جدیدی موسوم به «جابهجایی الکتریکی» (Electric Displacement) تعریف میکنند که حاصل جمع بردار میدان الکتریکی و بردار قطبش به شکل زیر است:
(7)
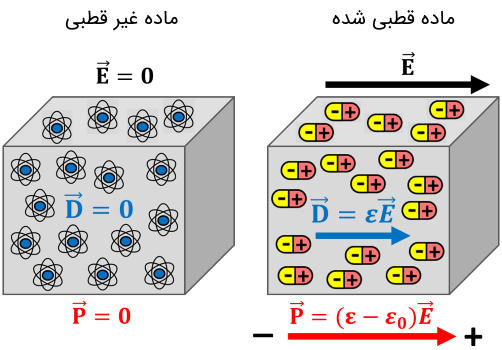
با استفاده از رابطه (5) نتیجه میشود:
(8)
در واقع جابهجایی الکتریکی ()، برداری است که در معادلات الکترواستاتیک و معادلات ماکسول پدیدار شده و متشکل از میدان الکتریکی و بردار قطبش است. از قانون گاوس نتیجه میشود که انتگرال جابهجایی الکتریکی () روی یک سطح بسته، شار عبوری از آن سطح را نتیجه میدهد. به عبارت دیگر میتوانیم گذردهی یک محیط (ماده) را میزان توانایی آن محیط در متمرکز کردن چگالی شار الکتریکی در خود بدانیم. از قانون گاوس داریم:
(9)
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^













خیلی ممنونم از این توضیحات روان و مفید. من رشته ام فیزیک نیست و بنا به نیازم باید این مطلب رو یاد میگرفتم. بعد از مرور چندین سایت، اینجا تنها جایی بود که مطلب رو کاملا متوجه شدم.
با سلام؛
خوشحالیم که مطالعه این مطلب برای شما مفید بوده است.
با تشکر از همراهی شما با مجله فرادرس
سلام میخواستم بپرسم با افزایش یا کاهش ثابت دی الکتریک چه تغییری در خواص گرمایشی ایجاد میشود؟ یعنی اگه ثابت دی الکتریک کم بشود سرعت گرمایش کم میشود؟
سلام ببخشید بهترین ثابت دی الکتریک چیه؟از همه ،از نظر بالاترین ولتاژ شکست و از نظر بیشترین افزایش ظرفیت خازن
سلام سپاس از مطالب خوبتون مطالب با رفرنس باشند بهتر هست
سلام، وقت شما بخیر؛
منابع تمامی مطالب فرادرس در انتهای آنها و بعد از بخش معرفی آموزشها و مطالب مرتبط ذکر شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
سلام وقتتون بخیر
عااییی بود
فقط این قسمت زیر شکل (1):
اما در یک اتم –>ناقطبیده<– توزیع الکترونها یکنواخت نبوده و در قسمتی از اتم جمعیت الکترونها بیشتر است
قسمتی که مشخص کردم رو اصلاح بفرمایید.
در کل بسیار عالی تشکر
سلام و روز شما به خیر؛
از توجه و دقت نظر شما سپاسگزاریم. این مورد در متن اصلاح و ویرایش شد.
از اینکه با فرادرس همراه هستید خرسندیم.
با سلام سوالی داشتم۱.۳۵ضریب شکست چه ماده ای هست؟
با سلام ممنون از اطلاعات خوبتون به من خیلی کمک کرد مطالب بخش دی الکتریک ، فقط اگه امکانش باشه ممنون میشم رفرنس هایی که این اطلاعات رو ازش جمع آوری کردین هم بزارین.