دستور Sparse در متلب | به زبان ساده

در این مطلب قصد داریم در مورد ماتریس Sparse و ویژگی‌های آن و نحوه ساخت این ماتریس در متلب صحبت کنیم. در مورد ماتریس می‌دانیم که ویژگی دو بعدی در ریاضیات است که می‌تواند دارای $$m$$ سطر و $$n$$ ستون باشد. در این مطلب در مورد نوع ویژه‌ای از ماتریس یعنی ماتریس Sparse در متلب صحبت خواهیم کرد.

ماتریس Sparse چیست؟

اگر در یک ماتریس بیشتر عناصر آن صفر باشند ماتریس را یک ماتریس Sparse می‌نامیم. به همین دلیل در ترجمه فارسی به این کمیت «ماتریس تُنُک» (Sparse Matrix) نیز می‌گویند.

فیلم آموزش برنامه نویسی متلب MATLAB در فرادرس

کلیک کنید

این ماتریس‌ها داده‌های دوبل یا منطقی را فراهم می‌کنند که درصد زیادی از اعضای آن‌ها صفر است. این موضوع زمانی مهم می‌شود که بدانیم ماتریس‌های کامل (یا متراکم) هر یک از عناصر ماتریس را صرف نظر از مقدار در حافظه ذخیره می‌کنند، در حالیکه ماتریس‌های تُنُک فقط عناصر غیر صفر و شاخص‌های ردیف آن‌ها را ذخیره می‌کنند. به همین دلیل استفاده از ماتریس‌های تُنُک می‌تواند مقدار حافظه مورد نیاز برای ذخیره اطلاعات را به میزان قابل توجهی کاهش دهد.

ماتریس Sparse چه ویژگی‌هایی دارد؟

در مورد ویژگی‌های این ماتریس باید به دو نکته اشاره کرد:

• ذخیره سازی: در این ماتریس عناصر غیر صفر کمتری نسبت به مقدار صفر وجود دارند و بنابراین می‌توان از حافظه کمتری برای ذخیره عناصر غیر صفر استفاده کرد.
• زمان محاسبه: با طراحی منطقی یک ساختار داده که فقط عناصر غیر صفر را بررسی می‌کند می توان زمان محاسبه را کاهش داد.

ماتریس زیر را در نظر بگیرید:

$$\begin{pmatrix}
0 & 0 & 3 & 0 & 4
\\ 0 & 0 & 5 & 7 & 0
\\ 0 & 0&0&0&0
\\ 0&2&6&0&0
\end{pmatrix}$$

نمایش یک ماتریس تُنُک توسط یک آرایه دوبُعدی منجر به هدر رفتن مقدار زیادی حافظه می‌شود زیرا صفرها در ماتریس در بیشتر موارد فایده‌ای ندارند. بنابراین ما به جای ذخیره صفرها و عناصر غیر صفر فقط عناصر غیر صفر را ذخیره می‌کنیم. این موضوع به معنای ذخیره عناصر غیر صفر با سه عدد سطر، ستون و مقدار است.

بدین ترتیب نمایش ماتریس Sparse را می‌توان به دو روش مختلف انجام داد:

1. نمایش آرایه
2. نمایش لیست لینک داده شده

نمایش ماتریس Sparse به وسیله آرایه

در این روش از یک آرایه دوبُعدی برای نشان دادن یک ماتریس پراکنده یا تُنُک استفاده می‌شود که در آن سه ردیف وجود دارد:

• Row: شاخص سطری که عنصر غیر صفر در آن قرار دارد.
• Column: شاخص ستونی که عنصر غیر صفر در آن قرار دارد.
• مقدار: مقدار عنصر غیر صفر واقع در شاخص سطر و ستون مشخص شده.

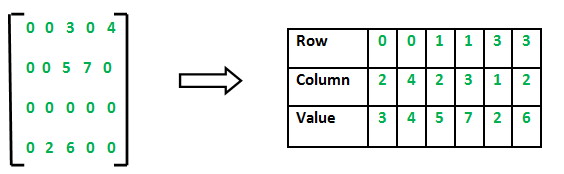
در تصویر زیر یک ماتریس Sparse با این روش نمایش داده شده است. همانطور که مشاهده می‌کنید در سطر صفرم و در ردیف دوم مقدار غیر صفر 3 قرار دارد پس برای این مقدار در جدول برای سطر صفرم و ردیف دوم مقدار 3 را ثبت می‌کنیم.

نکته مهم این است که در کدهایی مانند C++ یا پایتون شمارنده از صفر آغاز می‌شود و به همین دلیل در تصاویر (1) و (2) نیز شمارش سطر و ستون از صفر آغاز می‌شود.

چگونه یک ماتریس Sparse را در C++ به روش آرایه نمایش دهیم؟

ماتریس تصویر (1) که یک ماتریس با 4 سطر و 5 ستون است را در نظر بگیرید، می‌خواهیم این ماتریس به صورت آرایه در C++ نمایش دهیم برای این کار به صورت زیر عمل می‎‌کنیم:

1#include <iostream>
2#include<stdio.h> 
3
4int main() 
5{ 
6	// Assume 4x5 sparse matrix 
7	int sparseMatrix[4][5] = 
8	{ 
9		{0 , 0 , 3 , 0 , 4 }, 
10		{0 , 0 , 5 , 7 , 0 }, 
11		{0 , 0 , 0 , 0 , 0 }, 
12		{0 , 2 , 6 , 0 , 0 } 
13	}; 
14
15	int size = 0; 
16	for (int i = 0; i < 4; i++) 
17		for (int j = 0; j < 5; j++) 
18			if (sparseMatrix[i][j] != 0) 
19				size++; 
20
21	// number of columns in compactMatrix (size) must be 
22	// equal to number of non - zero elements in 
23	// sparseMatrix 
24	int compactMatrix[3][size]; 
25
26	// Making of new matrix 
27	int k = 0; 
28	for (int i = 0; i < 4; i++) 
29		for (int j = 0; j < 5; j++) 
30			if (sparseMatrix[i][j] != 0) 
31			{ 
32				compactMatrix[0][k] = i; 
33				compactMatrix[1][k] = j; 
34				compactMatrix[2][k] = sparseMatrix[i][j]; 
35				k++; 
36			} 
37
38	for (int i=0; i<3; i++) 
39	{ 
40		for (int j=0; j<size; j++) 
41			printf("%d ", compactMatrix[i][j]); 
42
43		printf("\n"); 
44	} 
45	return 0; 
46} 

در این مثال همان طور که ملاحظه می‌کنید یک ماتریس 4 در 5 داریم که 6 عنصر آن غیر صفر است. پس ماتریسی می‌سازیم که سه سطر (سطر، ستون و مقدار عناصر غیر صفر ماتریس Sparse) و به اندازه عناصر غیر صفر ماتریس اولیه ستون داشته باشد. یعنی با یک دستور if اعلام می‌کنیم که اگر مقدار آرایه ماتریس غیر صفر بود به size یک واحد اضافه شود.

بعد از ساخت ماتریس مورد نظر تنها لازم است که شماره سطر و ستون و مقدار را وارد کنیم. در نهایت خروجی کد بالا به صورت زیر است:

$$\begin{matrix}
0 & 0 & 1 & 1 & 3& 3
\\ 2 & 4 & 2 & 3 & 1&2
\\ 3 & 4&5&7&2&6
\end{matrix}$$

چگونه یک ماتریس Sparse را در پایتون 3 روش آرایه نمایش دهیم؟

مجدداً برای ماتریس تصویر (1) این کد را در پایتون 3 بررسی می‌کنیم.

فیلم آموزش محاسبات عددی در پایتون Python در فرادرس

کلیک کنید

1# Python program for Sparse Matrix Representation 
2# using arrays 
3
4# assume a sparse matrix of order 4*5 
5# let assume another matrix compactMatrix 
6# now store the value,row,column of arr1 in sparse matrix compactMatrix 
7
8sparseMatrix = [[0,0,3,0,4],[0,0,5,7,0],[0,0,0,0,0],[0,2,6,0,0]] 
9
10# initialize size as 0 
11size = 0
12
13for i in range(4): 
14	for j in range(5): 
15		if (sparseMatrix[i][j] != 0): 
16			size += 1
17
18# number of columns in compactMatrix(size) should 
19# be equal to number of non-zero elements in sparseMatrix 
20rows, cols = (3, size) 
21compactMatrix = [[0 for i in range(cols)] for j in range(rows)] 
22
23k = 0
24for i in range(4): 
25	for j in range(5): 
26		if (sparseMatrix[i][j] != 0): 
27			compactMatrix[0][k] = i 
28			compactMatrix[1][k] = j 
29			compactMatrix[2][k] = sparseMatrix[i][j] 
30			k += 1
31
32for i in compactMatrix: 
33	print(i) 

روش کار شبیه به کد C++ است فقط همانطور که قطعاً می‌دانید روش تعریف ماتریس در پایتون با C++ کمی متفاوت است. در این حالت نیز خروجی شبیه به حالت قبل است و داریم:

$$\begin{bmatrix}
0 & 0 & 1 & 1 & 3& 3
\\ 2 & 4 & 2 & 3 & 1&2
\\ 3 & 4&5&7&2&6
\end{bmatrix}$$

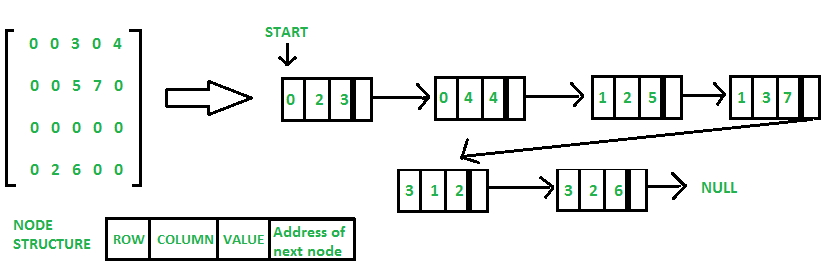
نمایش ماتریس Sparse به وسیله لیست لینک داده شده

در لیست لینک شده هر بخش دارای چهار قسمت است که این چهار قسمت به صورت زیر تعریف می‌شوند:

• سطر: شاخص سطری که عنصر غیر صفر در آن قرار دارد.
• ستون: شاخص ستونی که عنصر غیر صفر در آن قرار دارد.
• مقدار: مقدار عنصر غیر صفر واقع در شاخص (سطر ، ستون) است.
• گره بعدی: آدرس عنصر بعدی غیر صفر در ماتریس

مزایای محاسباتی ماتریس‌های Sparse در متلب

مدیریت حافظه

استفاده از ماتریس‌های Sparse برای ذخیره داده‌هایی که حاوی تعداد زیادی مقدار با ارزش صفر است، هم می‌تواند میزان قابل توجهی از حافظه را حفظ کند و هم سرعت پردازش داده‌ها را تسریع کند. Sparse ویژگی است که می‌توانید به هر ماتریس دو بعدی در متلب که از عناصر دوبل یا منطقی تشکیل شده اختصاص دهید.

فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی در فرادرس

کلیک کنید

ویژگی Sparse به متلب اجازه می‌دهد تا فقط عناصر غیر صفر ماتریس را به همراه شاخص‌های آن‌ها ذخیره کند. با حذف عملیات روی عناصر صفر زمان محاسبات کاهش پیدا می‌کند.

برای ماتریس‌های کامل، متلب هر عنصر ماتریسی را به صورت داخلی ذخیره می‌کند و عناصر با ارزش صفر به همان میزان فضای ذخیره‌سازی مشابهِ سایر عناصر ماتریس نیاز دارند. با این حال برای ماتریس‌های Sparse متلب فقط عناصر غیر صفر و شاخص‌های آن‌ها را ذخیره می‌کند.

برای ماتریس‌های بزرگ با درصد بالایی از عناصر با ارزش صفر این طرح میزان حافظه مورد نیاز برای ذخیره داده را به میزان قابل توجهی کاهش می‌دهد.

دستور whos اطلاعات زیادی در مورد ذخیره‌سازی یک ماتریس از جمله اندازه و کلاس ذخیره‌سازی فراهم می‌کند. به عنوان مثال دستور whos اطلاعات مربوط به نسخه Sparse و کامل یک ماتریس را به صورت زیر نشان می‌‌دهد:

1M_full = magic(1100);          % Create 1100-by-1100 matrix.
2M_full(M_full > 50) = 0;       % Set elements >50 to zero.
3M_sparse = sparse(M_full);     % Create sparse matrix of same.
4
5whos

با اجرای دستور whos خروجی را به صورت زیر خواهیم داشت:

1  Name             Size                Bytes  Class     Attributes
2
3  M_full        1100x1100            9680000  double              
4  M_sparse      1100x1100               9608  double    sparse

توجه داشته باشید که تعداد بایت‌های استفاده شده در حالت پراکنده کمتر است زیرا عناصر با ارزش صفر ذخیره نمی‌شوند.

کارایی محاسباتی در ماتریس Sparse

ماتریس‌های Sparse از نظر کارایی محاسباتی نیز دارای مزایای قابل توجهی هستند. برخلاف عملیات با ماتریس کامل عملیات با ماتریس پراکنده یا Sparse محاسبات سطح پایین غیرضروری را انجام نمی‌دهد (مانند جمع‌ها یا ضرب‌های مربوط به عناصر صفر). این ویژگی‌ها می‌تواند منجر به بهبودهای چشمگیری در زمان اجرا برای برنامه‌هایی شود که با مقدار زیادی داده پراکنده کار می‌کنند.

چگونه در متلب ماتریس Sparse تولید کنیم؟

تمام عملیات ریاضی، منطقی و نمایه‌سازی در متلب را می‌توان در ماتریس‌های Sparse یا ترکیبی از ماتریس‌های Sparse و عادی انجام داد. عملیات روی ماتریس Sparse یک ماتریس Sparse می‌دهد و عملیات روی ماتریس عادی یک ماتریس عادی را برمی‌گرداند.

فیلم آموزش محاسبات انتگرال با متلب و میپل MATLAB و Maple در فرادرس

کلیک کنید

متلب هرگز به طور خودکار ماتریس تُنُک ایجاد نمی‌کند. در حقیقت شما باید تعیین کنید که آیا یک ماتریس آن قدر اعضای صفر دارد که بخواهید از دستورهای ماتریس Sparse استفاده کنید یا خیر.

چگالی یک ماتریس تعداد عناصر غیر صفر تقسیم بر تعداد کل عناصر ماتریس است. برای ماتریس M این کمیت را می‌توان به صورت زیر تعیین کرد:

1nnz(M) / prod(size(M));

یا

1nnz(M) / numel(M);

ماتریس‌هایی با چگالی بسیار کم اغلب کاندیداهای خوبی برای استفاده از قالب Sparse متلب هستند.

تبدیل یک ماتریس به ماتریس Sparse در متلب

در متلب می‌توانید به راحتی یک ماتریس را با استفاده از تابع Sparse به یک ماتریس تُنُک یا Sparse تبدیل کنید. این کار را به راحتی در برنامه خود با یک دستور if می‌توانید اعمال کنید که اگر برای ماتریس A چگالی عناصر صفر به کل از یک عدد ثابت کمتر باشد دستور Sparse برای ماتریس مورد نظر صورت بگیرد.

ماتریس A را در زیر نظر بگیرید، با استفاده از دستور Sparse در متلب می‌توان به راحتی این تبدیل را انجام داد:

1A = [ 0   0   0   5
2      0   2   0   0
3      1   3   0   0
4      0   0   4   0];
5S = sparse(A)

به این ترتیب خروجی S به صورت زیر و یک تابع Sparse است.

1 S =
2     
3   (3,1)        1
4   (2,2)        2
5   (3,2)        3
6   (4,3)        4
7   (1,4)        5

در نتیجه به راحتی و با دستور Sparse می‌توان یک ماتریس از حالت عادی را به حالت Sparse نمایش داد. شمارنده در متلب از 1 آغاز می‌شود و به همین دلیل شما مشاهده می‌کنید که برای خروجی متلب سطر سوم و ستون اول مقدار 1 را دارد و الی آخر.

همان طور که بالاتر نیز توضیح دادیم نمایش ماتریس تُنُک عناصر غیر صفر S را به همراه شاخص‌های سطر و ستون آنها لیست می‌کند و عناصر بر اساس ستون‌ها مرتب شده‌اند.

با استفاده از تابع full می‌توانید یک ماتریس Sparse را مجدداً به فضای ذخیره‌سازی کامل تبدیل کنید به شرطی که درجه ماتریس خیلی بزرگ نباشد. به عنوان مثال دستور $$A=full(S)$$ تبدیل مثال را معکوس می‌کند و یک ماتریس کامل را می‌دهد. این تبدیل و عکس تبدیل را می‌توانید در تصویر (3) مشاهده کنید.

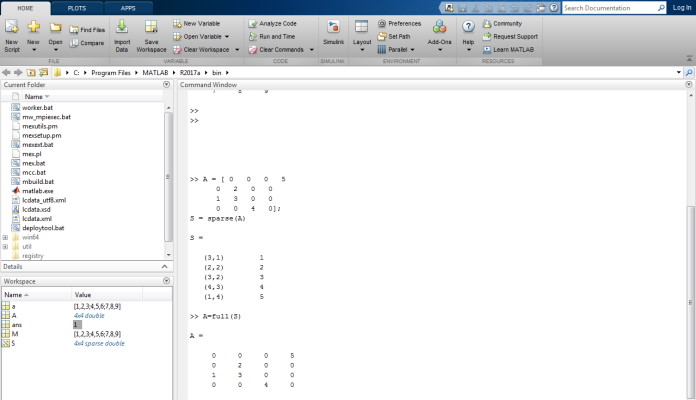
تبدیل ماتریس کامل به ماتریس Sparse از این روش خیلی متداول نیست مخصوصاً اگر حجم داده‌ها خیلی زیاد باشد. با این حال اگر مرتبه یک ماتریس کوچک باشد به نوعی که ذخیره ماتریس به صورت کامل امکان پذیر باشد می‌توان از این روش سود جست در غیر این صورت روش مذکور کارآمدی قابل توجهی ندارد و استفاده نمی‌شود. در این حالت باید به صورت مستقیم ماتریس Sparse را تولید کرد.

ایجاد مستقیم ماتریس‌های Sparse در متلب

می‌توانید با استفاده از تابع Sparse با پنج آرگومان از لیست عناصر غیر صفر، یک ماتریس پراکنده ایجاد کنید. دستور زیر را در نظر بگیرید:

1S = sparse(i,j,s,m,n)

که i و j به ترتیب بردار شاخص‌های سطر و ستون برای عناصر غیر صفر ماتریس هستند. s بردار مقادیر غیر صفر است که شاخص‌های آن با جفت‌های مربوطه (i، j) مشخص می‌شوند. m تعداد سطر و n تعداد ستون ماتریس است. بدین ترتیب ماتریس S بخش قبلی را می‌توان مستقیماً با استفاده از دستور زیر تولید کرد:

1S = sparse([3 2 3 4 1],[1 2 2 3 4],[1 2 3 4 5],4,4)

و خروجی همانند حالت قبل خواهد بود. در حقیقت شما اعلام می‌‌کنید که در سطر 3 و ستون 1 مقدار غیر صفر 1 را دارید و همچنین بیان می‌کنید که ماتریس ابتدایی یک ماتریس 4 در 4 است.

دستور Sparse دارای شکل‌های دیگری نیز است. مثال بالا از فرمی استفاده می‌کند که تعداد عناصر غیر صفر را در ماتریسی با توجه به طول بردار تنظیم می‌کند.

در صورت تمایل می‌توانید یک آرگومان ششم را اضافه کنید که حداکثر بزرگتری را مشخص می‌کند و به شما این امکان را می‌دهد تا عناصر غیر صفر را بعداً بدون تخصیص مجدد ماتریس Sparse اضافه کنید.

مثال دیگری از ایجاد یک ماتریس تُنُک یک ماتریس مثلثی است که عناصر روی قطر اصلی برابر با $$-2s$$ و عناصر روی قطر بالا و پایین قطر اصلی برابر با $$1s$$ است. روش های زیادی برای تولید ماتریس تُنُک این ماتریس وجود دارد که در اینجا یکی از آن‌ها را بررسی می‌کنیم.

1n = 5;
2D = sparse(1:n,1:n,-2*ones(1,n),n,n);
3E = sparse(2:n,1:n-1,ones(1,n-1),n,n);
4S = E+D+E'

که با اجرای این دستور خروجی به صورت زیر به دست می‌آید:

1S =
2
3   (1,1)       -2
4   (2,1)        1
5   (1,2)        1
6   (2,2)       -2
7   (3,2)        1
8   (2,3)        1
9   (3,3)       -2
10   (4,3)        1
11   (3,4)        1
12   (4,4)       -2
13   (5,4)        1
14   (4,5)        1
15   (5,5)       -2

حال اگر بخواهیم ماتریس کامل را نمایش دهیم از دستور $$F=full(S)$$ خروجی به صورت زیر خواهد بود:

$$F=\\
\begin{matrix}
-2 & 1 & 0 & 0 & 0
\\ 1 & -2 & 1 & 0 & 0
\\ 0&1&-2&1&0
\\0&0&1&-2&1
\\0&0&0&1&-2
\end{matrix}$$

ایجاد ماتریس‌های Sparse با استفاده از عناصر قطری

ایجاد ماتریس های تُنُک بر اساس عناصر قطری آن‌ها عملی رایج است ، بنابراین تابع spdiags این وظیفه را به صورت زیر انجام می‌دهد:

1S = spdiags(B,d,m,n)

برای ایجاد یک ماتریس خروجی با نام S با مرتبه m در n که عناصر روی قطر p است به صورت زیر عمل می‌کنیم:

• B ماتریسی با اندازه $$min(m,n)$$ با p است. ستون‌های B مجموع مقادیر قطر S هستند.
• d برداری با طول p است كه عناصر صحیح آن مشخص می‌كند كه كدام قطر از S با ستون‌های B مقدار گذاری شوند.

در حقیقت در این حالت عناصر موجود در ستون j از B، قطر مشخص شده توسط عنصر j از d را پر می‌کنند.

برای درک بهتر این روش مثال زیر را در نظر بگیرید:

1B = [ 41    11     0
2      52    22     0
3      63    33    13
4      74    44    24 ];
5
6d = [-3
7      0
8      2];

می‌خواهیم از این ماتریس‌ و بردار برای ایجاد یک ماتریس تُنُک 7 در 4 استفاده کنید، یعنی داریم:

1A = spdiags(B,d,7,4)

بدین ترتیب در خروجی داریم:

1A =
2
3   (1,1)       11
4   (4,1)       41
5   (2,2)       22
6   (5,2)       52
7   (1,3)       13
8   (3,3)       33
9   (6,3)       63
10   (2,4)       24
11   (4,4)       44
12   (7,4)       74

شکل کامل ماتریس A را با دستور $$full(A)$$ می‌توان به دست آورد و خواهیم داشت:

$$ans=\\
\begin{matrix}
11 & 0 & 13 & 0
\\ 0 & 22 & 0 & 24
\\ 0&0&33&0
\\41&0&0&44
\\0&52&0&0
\\0&0&63&0
\\0&0&0&74
\end{matrix}$$

همان طور که از مثال بالا می‌بینید ستون اول ماتریس B در قطر $$-3$$، ستون دوم در قطر 0 و ستون سوم در قطر 2 از ماتریس پراکنده A مقدارگذاری شده است.

spdiags همچنین می‌تواند عناصر قطری را از یک ماتریس Sparse استخراج کند یا عناصر قطری ماتریس را با مقادیر جدید جایگزین کند.

وارد کردن ماتریس‌های Sparse در متلب

می‌توان ماتریس‌های Sparse را از محاسبات خارج از محیط متلب وارد متلب کرد. برای وارد کردن پرونده‌های متنی حاوی لیست شاخص‌ها و عناصر غیر صفر از تابع spconvert همراه با دستور load استفاده کنید. به عنوان مثال یک فایل متنی سه ستونی T.dat را در نظر بگیرید که ستون اول لیستی از شاخص‌های ردیف، ستون دوم لیستی از شاخص‌های ستون و ستون سوم لیستی از مقادیر غیر صفر است. این دستور T.dat را در متلب بارگذاری کرده و به یک ماتریس Sparse تبدیل می‌کند:

1load T.dat
2S = spconvert(T)

دستورات save و load همچنین می‌توانند ماتریس‌های Sparse را که به عنوان داده‌های باینری در پوشه‌های MAT ذخیره شده‌اند را پردازش کنند.

دستورهای موجود در متلب برای ماتریس Sparse چیست؟

دستورهای مربوط به ماتریس Sparse را می‌توان به شش دسته کلی تقسیم‌بندی کرد که به ترتیب عبارتند از:

1. تولید ماتریس Sparse
2. تغییرات در ماتریس Sparse
3. مرتب‌سازی مجدد الگوریتم‌ها
4. الگوریتم‌های تکرار و پیش شرط
5. ویژه مقدار و مقدار منفرد
6. تحلیل ساختاری

در ادامه هر یک از دستورهای مورد استفاده در هر گروه و کاربرد آن را به طور خلاصه شرح خواهیم داد.

دستورهای تولید ماتریس Sparse

دستور spalloc

با استفاده از این دستور در متلب می‌توانید فضای مشخص به ماتریس Sparse اختصاص دهید و در هر مرحله به ماتریس مقداردهی کنید. بدین ترتیب با دستور $$S=spalloc(m,n,nz)$$ یک ماتریس پراکنده با اندازه m در n تولید می‌شود که nz فضا را برای مقادیر غیر صفر حفظ می‌کند.

دستور spdiags

این دستور را در قسمت‌های قبل معرفی و بررسی کردیم. در حقیقت این ویژگی یک ماتریس قطری ایجاد می‌کند که قطرهای مشخصی در آن غیر صفر هستند و با استفاده از این دستور اجزای غیر صفر ماتریس نمایش داده می‌شوند.

دستور speye

این دستور یک ماتریس واحد پراکنده ایجاد می‌کند و به چند روش نمایش داده می‌شود.

1. $$speye(n)$$ یک ماتریس واحد n در n ایجاد می‌کند که قطر اصلی آن 1 و بقیه عناصر صفر هستند.
2. $$speye(n,m)$$ یک ماتریس واحد n در m ایجاد می‌کند که قطر اصلی آن 1 و بقیه صفر هستند.

دستور sprand

این دستور نیز یک ماتریس sparse به صورت تصادفی تولید می‌کند.

1. $$sprand(S)$$ همان ساختار پراکنده S را دارد اما ورودی‌های تصادفی آن توزیع یکنواخت دارند.
2. $$sprand(m,n,density)$$ یک ماتریس پراکنده تصادفی m در n با توزیع تقریبی یکنواخت و غیر صفر $$m*n*density$$ تولید می‌کند.

دستور sprandn

یک ماتریس sparse تصادفی نرمال را تولید می‌کند. نمایش ورودی این دستور شبیه به sprand است و تنها تفاوت در خروجی این است که یک ماتریس Sparse نرمال تولید می‌کند.

دستور sprandsym

در این دستور یک ماتریس Sparse تصادفی متقارن تولید می‌شود. در این حالت ورودی به صورت  $$sprandsym(S)$$ یا $$sprandsym(n,density)$$ است.

دستور sparse

در مورد این دستور در قسمت‌های قبل به طور مفصل صحبت کردیم. این دستور یک ماتریس پراکنده تولید می‌کند و به چندین شکل مختلف می‌تواند ورودی دریافت کند که عبارتند از:

1. S = sparse(A)
2. S = sparse(m,n)
3. S = sparse(i,j,v)
4. S = sparse(i,j,v,m,n)
5. S = sparse(i,j,v,m,n,nz)

دستور spconvert

با استفاده از این دستور می‌توان فایل ماتریس sparse تولید شده در محیط‌های دیگر را به عنوان ورودی به متلب داد و روی آن محاسبات انجام داد.

دستورات مربوط به تغییرات روی ماتریس Sparse

دستور issparse

از این دستور برای تشخیص این موضوع که آیا ماتریس پراکنده است یا خیر استفاده می‌شود.

دستور nnz

برای تشخیص تعداد عناصر غیر صفر در ماتریس استفاده می‌شود.

دستور nonzeros

استفاده از این دستور تمام عناصر غیر صفر را به صورت ستونی استخراج می‌کند.

دستور nzmax

این دستور مقدار فضایی که به عناصر غیر صفر اختصاص داده شده را به عنوان خروجی مشخص می‌کند.

دستور spfun

با استفاده از این دستور می‌توان به عناصر غیر صفر یک ماتریس پراکنده یا sparse یک تابع اعمال کرد. برای مثال دستور $$spfun(@exp,S)$$ تابع exp را به تمام عناصر ماتریس پراکنده S اعمال می‌کند.

دستور spones

این دستور عناصر ماتریس پراکنده غیر صفر را با یک جایگزین می‌کند.

دستور spy

این دستور الگوی پراکندگی ماتریس را تصویر می‌کند.

دستور find

یافتن شاخص‌ها و مقادیر عناصر غیر صفر در ماتریس توسط این دستور صورت می‌گیرد.

دستور full

تبدیل ماتریس پراکنده یا sparse به فضای ذخیره‌سازی کامل توسط این دستور صورت می‌گیرد.

برای آشنایی بیشتر با دستورات مربوط به ماتریس sparse یا پراکنده در متلب ‌می‌توانید این مطلب را در وبسایت mathworks مطالعه کنید. دقت کنید در ورود به وبسایت mahworks وی پی ان دستگاه خود را روشن کنید.

همچنین باید عنوان کرد که جزئیات کار با ماتریس‌های پراکنده، تُنُک یا sparse شبیه به ماتریس معمولی می‌باشد با این تفاوت که در این حالت شما به طور بهینه‌تری از فضای حافظه استفاده می‌کنید و در مدت زمان انجام محاسبات صرفه جویی خواهید کرد.

جمع‌بندی

در این مطلب به معرفی و بررسی ویژگی‌های ماتریس Sparse پرداختیم و نشان دادیم با استفاده از این ماتریس خصوصاً در بررسی داده‌های بزرگ و با حجم بالا می‌توان در استفاده از فضای حافظه و زمان اجرای محاسبات بهینه عمل کرد، زیرا این ماتریس تنها عناصر غیر صفر را ذخیره می‌کند. همچنین نحوه ایجاد این ماتریس و نمایش آن را در پایتون، C++ و با جزئیات بیشتر در متلب بررسی کردیم.