خازن در جریان متناوب – به زبان ساده

در این مقاله قصد داریم تا با زبانی ساده رفتار خازن در جریان متناوب را بررسی کنیم. وقتی که یک خازن در مداری با منبع تغذیه متناوب AC قرار می‌گیرد، بسته به فرکانس جریان تولیدی منبع تغذیه و ظرفیتش از خود مقاومت نشان می‌دهد.

احتمالاً با عملکرد خازن در جریان‌های ثابت آشنایید. زمانی که یک خازن به یک منبع ولتاژ ثابت DC متصل می‌شود، شارژ شده و پس از اینکه به طور کامل پر شد (تقریباً پس از ۵ ثابت زمانی آن) مانع از عبور جریان در مدار می‌شود. این خازن می‌تواند مانند یک باتری عمل کرده و در هنگام نیاز، انرژی درخواستی مدار را تامین کند.

حال اگر ما خازن را در یک مداری با منبع تغذیه متناوب قرار دهیم، خازن به طور متناوب با نرخی که فرکانس جریان متناوب تعیین می‌کند، شارژ و تخلیه می‌شود. در نتیجه بسته به فرکانس جریان متناوب، مقاومت خازنی موسوم به «راکتانس» (Reactance) می‌تواند متفاوت باشد.

می‌دانیم که مقدار بار، در واقع جریان الکترون‌ها روی صفحات خازن متناسب با تغییر ولتاژ دو سر خازن است ($$Q=CV$$). یعنی جریان در هر لحظه به صفحه مثبت خازن وارد می‌شود. اما اگر خازن را در مداری با جریان متناوب قرار دهیم، به دلیل عوض شدن جهت جریان در هر یک‌چهارم دوره ($$T=\frac{1}{۴f}$$)، علامت بار صفحات خازن نیز در هر یک‌چهارم دوره تغییر می‌کند. در این مقاله خواهیم دید که تغییر علامت بار صفحات که به معنی شارژ و تخلیه خازن است، سریع اتفاق نمی‌افتد، چرا که جریان و اختلاف پتانسیل دارای اختلاف فاز 90 درجه هستند. در نتیجه این امر را مشابه یک مقاومت در برابر شارژ و تخلیه در نظر می‌گیرند. برای توضیحات بیشتر در ادامه مقاله همراه ما باشید.

خازن در جریان متناوب

شکل زیر خازنی را نشان می‌دهد که در یک مدار ساده و  متصل به یک منبع ولتاژ متناوب، قرار گرفته است.

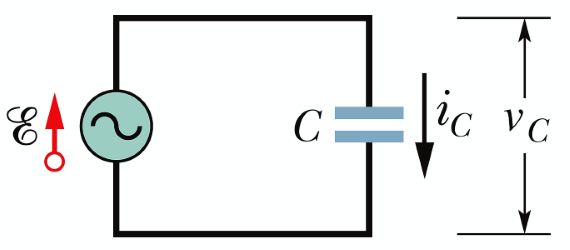
مطابق با شکل (۱) اختلاف پتانسیل دو سر خازن برابر با اختلاف پتانسیل منبع تغذیه متناوب است، در نتیجه:

$$v_{c}=V_{c}\sin\omega t$$
(1)

می‌دانیم که مقدار بار ذخیره شده در صفحات خازن طبق رابطه ($$Q=CV$$) به دست می‌آید. از آنجا که اختلاف پتانسیل دو سر خازن به طور متناوب تغییر می‌کند، مقدار بار روی صفحات نیز مطابق رابطه زیر به طور متناوب دچار تغییر می‌شود:

$$q_{c}=Cv_{c}=CV_{c}\sin\omega t$$
(2)

برای ادامه کار به جریان عبوری از خازن نیاز داریم. از آنجایی که جریان الکتریکی به صورت ($$i=\frac{dq}{dt}$$) تعریف می‌شود، داریم:

$$i_{c}=\frac{dq_{c}}{dt}=\omega CV_{c}\cos\omega t$$
(3)

برای اینکه معادله فوق، شبیه به معادله جریان متناوب عبوری از یک مقاوت، در واقع شبیه رابطه قانون اهم شود، نیاز است تا تغییراتی را در آن ایجاد کنیم. اولین کار تعریف ضریب $$\cos$$ است. این امر را با تعریف $$X_{c}$$ که ماهیتی مقاومتی دارد، انجام می‌دهیم. کمیت $$X_{c}$$ به «راکتانس خازنی» (Capacitive Reactance) معروف است.

$$X_{c}=\frac{1}{\omega C}=\frac{1}{2\pi fC}$$
(4)

همانطور که از رابطه فوق مشخص است، راکتانس خازنی تنها به مقدار ظرفیت خازن و فرکانس منبع تغذیه متناوب وابسته است. در مقاله «مدار مرتبه اول RC — از صفر تا صد» دیدیم که ثابت زمانی خازن برابر با $$\tau=RC$$ است. طبق این رابطه در سیستم جهانی SI، واحد C (ظرفیت خازنی) را می‌توانیم ثانیه بر اهم تعریف کنیم. در نتیجه واحد راکتانس خازنی طبق رابطه (4) همانند مقاومت، اهم است.

برای همانند‌سازی با ولتاژ که به صورت سینوسی تعریف شده و درک بهتر ریاضی می‌توان با استفاده از رابطه مثلثاتی زیر، رابطه (۳) را به فرم معادله (6) بازنویسی کرد:

$$\cos \omega t=\sin (\omega t+90)$$
(5)

در نتیجه:

$$i_{c}=\frac{V_{c}}{X_{c}}\sin(\omega t+90)$$
(6)
$$i_{c}=I_{c}\sin(\omega t+90)$$
(7)

رابطه فوق بیان می‌کند که جریان به اندازه 90 درجه با ولتاژ اعمالی، اختلاف فاز، به طور دقیق‌تر تقدم فاز دارد. درستی رابطه (6) را می‌توان با انتقال منحنی سینوسی ولتاژ  به اندازه 90 درجه در جهت منفی بررسی کرد (شکل 2).

در رابطه (۷)، $$I_{c}$$ دامنه جریان (جریان $$rms$$) است. پس رابطه میان دامنه ولتاژ (ولتاژ $$rms$$) و دامنه جریان در خازنی که به یک منبع تغذیه متناوب متصل بوده، به صورت زیر است:

$$V_{c}=I_{c}X_{c}$$
(8)

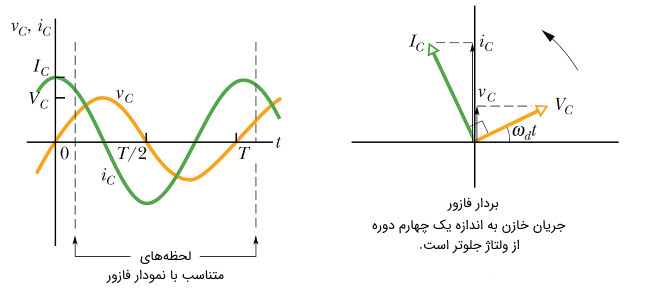
مطابق با شکل (3)، جریان $$i_{c}$$ و ولتاژ $$v_{c}$$ به اندازه $$\frac{\pi}{2}rad=90^{\circ}$$ یعنی یک چهارم دوره نسبت به هم اختلاف فاز دارند. با بررسی نمودار، پی میبریم که جریان $$i_{c}$$ یک چهارم دوره زودتر به بیشینه خود می‌رسد.

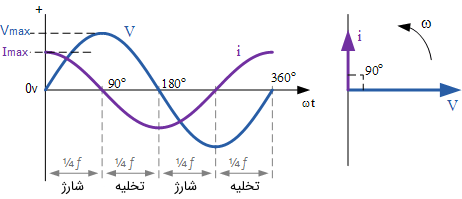
نمایش فازوری این امر نیز بیانگر مطالب گفته شده است. طبق شکل (۲) یا (۳)، فازور $$I_{c}$$ به انداز۰ 90 درجه جلوتر از فازور $$V_{c}$$ در جهت پادساعتگرد می‌چرخد.

تحلیل راکتانس خازنی

راکتانس خازنی طبق رابطه ($$X_{c}=\frac{1}{\omega C}=\frac{1}{2\pi fC}$$) با فرکانس نسبت عکس دارد. یعنی هر چه فرکانس منبع تغذیه افزایش پیدا کند، راکتانس کاهش می‌یابد شکل (4).

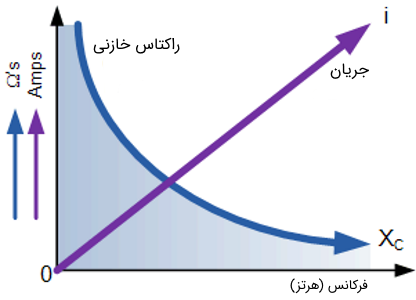
از نمودار شکل فوق و فرمول راکتانس خازنی پی میبریم که وقتی فرکانس به سمت صفر میل می‌کند (ولتاژ DC)، مقدار راکتانس $$X_{c}$$ به سمت بی‌نهایت میل کرده و خازن همچون کلید باز عمل می‌کند. همچنین در فرکانس‌های بی‌نهایت، راکتانس به سمت صفر میل کرده و با تقریب خوبی می‌شود خازن را در نظر نگرفت.

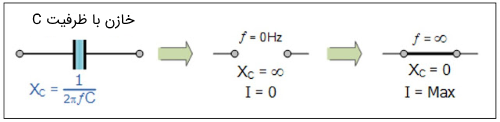
پس به طور خلاصه، راکتانس خازنی، مقاومت یک عنصر خازن در مقابل تغییر علامت جریان $$i_{c}$$ تعریف می‌شود.

مثال ۱

جریان rms منبع تغذیه‌ای را پیدا کنید که به یک خازن با ظرفیت $$4μF$$ متصل است و با فرکانس $$60Hz$$ در ولتاژ $$880V$$ کار می‌کند.

$$X_{c}=\frac{1}{\omega C}=\frac{1}{2\pi fC}=\frac{1}{2\pi \times60\times4\times10^{-6}}=663Ω$$

$$I_{rms}=\frac{V_{rms}}{X_{c}}=\frac{880V}{663Ω}=1.33A$$

مثال ۲

ظرفیت خازنی را پیدا کنید که در مداری با منبع تغذیه متناوب با فرکانس $$60Hz$$ قرار گرفته و راکتانس آن 390 اهم است.

$$X_{c}=\frac{1}{\omega C}=\frac{1}{2\pi fC}$$

$$C=\frac{1}{2\pi fX_{c}}$$

$$C=\frac{1}{2\pi \times60\times390}=6.8\mu F$$

مثال ۳

فرض کنید مطابق با مدار شکل (۱)، خازن در جریان متناوب با دامنه ولتاژ  $$36V$$ و فرکانس آن $$60Hz$$ باشد. ظرفیت خازن موجود در مدار نیز $$15μF$$ است. معادله سینوسی جریان $$i_{c}$$ عبوری از مدار را بنویسید.

$$v_{c}=V_{c}\sin(\omega t) , \omega=2\pi f$$

$$v_{c}=36\sin(120\pi t)$$

$$X_{c}=\frac{1}{\omega C}=\frac{1}{2\pi fC}$$

$$X_{c}=\frac{1}{\omega C}=\frac{1}{120\pi \times15\times10^{-6}}=177Ω$$

$$V_{c}=I_{c}X_{c} \Rightarrow I_{c}=0.203A$$

$$i_{c}=I_{c}\sin(\omega t+90)=0.203\sin(120\pi t+\frac{\pi}{2})$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۲
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش مدارهای الکتریکی ۱
• عناصر پسیو (Passive) در مدارهای AC — به زبان ساده
• خازن موازی -- به زبان ساده

^^