نازل و دیفیوزر – به زبان ساده

نازل به لولهای ترمودینامیکی گفته میشود که سطح مقطع آن متغیر است و به منظور افزایش سرعت جریان خروجی و کنترل جهت آن به کار میرود. در نتیجه این تغییر مومنتوم، نیرویی ایجاد میشود. این نیرو را میتوان به راحتی و با قرار دادن دست جلوی مسیر آب خروجی از شلنگ، آزمایش کرد.
به عنوان مثال، نازل موشک را در نظر بگیرید. خروج جرم از محفظه به سمت عقب و نیروی عکسالعمل حاصل از آن در جهت مخالف، باعث ایجاد حرکت نسبی میشود. همان اندازه که ملخ در ایجاد نیروی محرکه یک هواپیمای ملخی اهمیت دارد، نازل هم در موتور جت مهم است. زیرا تبدیل انرژی به انرژی جنبشی اگزوز و مومنتوم خطی ناشی از آن که منجر به نیروی تراست (thrust) میشود، همگی داخل نازل اتفاق میافتد. اولین بار، نازل در سال ۱۸۸۸ میلادی و به طور همزمان در آلمان و سوئد اختراع شد. در برخی کتابها، تمام لولههایی را که مطابق شکل زیر دارای سطح مقطع متغیر هستند، نازل مینامند. ولی در برخی کتابها نیز، آنها را به دو دسته نازل و دیفیوزر تقسیم میکنند. در این مقاله، عملکرد نازل و دیفیوزر را مطالعه کرده و برای هریک از آنها مثالی حل شده ارائه خواهیم کرد.
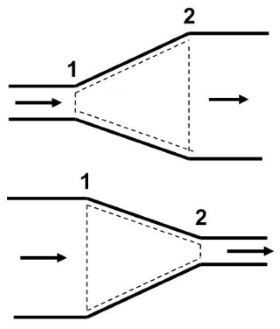
عملکرد نازل و دیفیوزر
کاربرد نازل و دیفیوزر گستره وسیعی را شامل شده و از موتورهای جت و فضاپیماها تا تجهیزات آبیاری فضای سبز را در بر میگیرد. نازل (nozzle) وسیلهایست که با کاهش فشار سیال، سرعت آن را افزایش میدهد. در سوی مقابل، دیفیوزر (diffuser) به وسیلهای گفته میشود که برعکس نازل عمل میکند. یعنی با کاهش سرعت سیال، فشار آن را بالا میبرد. سطح مقطع نازل در جهت عبور سیال، برای جریانهای فروصوت کاهش و برای جریانهای فراصوت، افزایش مییابد. خلاف این موضوع هم برای دیفیوزر صادق است.
نرخ انتقال حرارت بین سیال عبوری از داخل نازل و دیفیوزر و محیط اطراف آن معمولاً بسیار کوچک است ($$\large \dot{Q} \approx 0$$) و در بسیاری از مسائل میتوان از آن صرف نظر کرد. زیرا سرعت سیال، بسیار زیاد است و فرآیند به قدری سریع اتفاق میافتد که فرصتی برای انتقال حرارت باقی نمیماند. همچنین، کار انجام شده و تغییر انرژی پتانسیل در نازل و دیفیوزر نیز برابر صفر است. ولی به دلیل سرعت بالای سیال در عبور از آنها، تغییرات انرژی جنبشی بسیار محسوس است و باید محاسبه شود. شکل زیر را در نظر بگیرید. در ادامه، با ارائه دو مثال، معادلات ترمودینامیکی را در نازل و دیفیوزر به کار خواهیم برد.
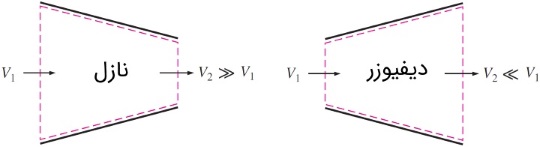
مثال 1
سؤال: هوا با دمای $$\large 10 \: ^\circ C$$ و فشار $$\large 80 \: kPa$$، به طور یکنواخت وارد دیفیوزر متعلق به یک موتور جت میشود. سرعت ورود هوا برابر با $$\large 200 \: m/s$$ است و مساحت مقطع ورودی را $$\large 0.4 \: m^2$$ فرض کنید. سرعت خروج هوا از دیفیوزر در مقایسه با سرعت ورودی، بسیار کوچکتر است. با توجه به این موارد، الف) نرخ دبی جرمی هوا، ب) دمای هوا در خروجی دیفیوزر را به دست آورید.
پاسخ: برای حل این مثال، شکل زیر را در نظر میگیریم. در اینجا، جرم به حجم کنترل، وارد و از آن خارج میشود. برای پایستگی جرم، رابطه $$\large \dot {m_1} = \dot {m_2} = \dot {m}$$ مفروض است.
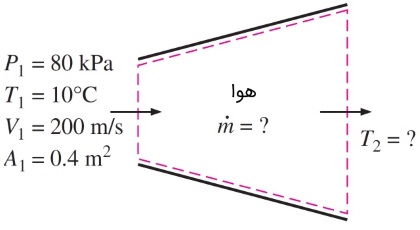
الف) برای تعیین نرخ دبی جرمی، باید ابتدا، حجم مخصوص هوا را پیدا کنیم. با استفاده از رابطه گاز کامل در ورودی دیفیوزر و به طریق زیر، ابتدا حجم مخصوص و سپس دبی جرمی را محاسبه میکنیم. از آنجایی که جریان یکنواخت است، نرخ دبی جرمی در سرتاسر دیفیوزر، ثابت و برابر مقدار به دست آمده زیر خواهد بود.
$$\large v_1 = \frac {R T _ 1} {P _ 1} = \frac {(0.287 \: kPa . m^3 / kg . K) \times (283 \:K)} {80 \: kPa} = 1.015 \: m^3 / kg \\~\\
\large \dot{ m} = \frac {1} {v_1} \times V_1 A_1 = \frac {1} {1.015 \:m^3/ kg} \times (200 \: m/s) (0.4 \:m^2) = \: 78.8 \: kg/ s$$
ب) با توجه به فرضیههای صورت سؤال، پایستگی انرژی را میتوان به شکل زیر بیان کرد.
$$\large \dot{E}_{in} - \dot {E} _ {out} \: = \: \frac {dE_{system}} {dt} \: = \: 0$$
در رابطه بالا، $$\large \dot{E}_{in} - \dot {E} _ {out} $$ نرخ مجموع انرژی انتقالی از طریق گرما، کار و جرم را نشان میدهد. از سوی دیگر، عبارت $$\large \frac {dE_{system}} {dt}$$ نیز نشان دهنده نرخ تغییر انرژیهای درونی، جنبشی و پتانسیل است که در نازل برابر صفر فرض میشود. در نتیجه، رابطه $$\large \dot{E}_{in} \: = \dot {E} _ {out}$$ برقرار خواهد بود. این رابطه را با در نظر گرفتن صفر بودن نرخ انتقال حرارت، کار و تغییر انرژی پتانسیل، به شیوه زیر بسط میدهیم.
$$\large \dot{m} \: (h_1 + \frac {V^2_1} {2}) \: = \dot {m} \: (h_2 + \frac {V^2_2} {2}) \\~\\
\large h_2 \: = h_1 \: - \frac {V^2_2 - V^2_1} {2}$$
سرعت خروج از دیفیوزر، در مقایسه با سرعت ورود به آن، بسیار کوچکتر است ($$\large V_2 \ll V_1$$). بنابراین، میتوان از انرژی جنبشی در خروجی صرف نظر کرد. آنتالپی هوا در ورودی دیفیوزر با کمک جداول ترمودینامیک برابر با مقدار $$\large h_1 = h _ {@ \: 283 K} = 283.14 \: kJ/kg$$ است. در نتیجه با جایگذاری این مقدار در رابطه آخر، مقدار آنتالپی در خروجی به صورت زیر به دست میآید.
$$\large h_2 \: = 283.14 \: kJ/kg \: - \frac {0 - (200 \: m/s)^2} {2} (\frac {1 kJ/kg} {1000 \: m^2/s^2}) \: = \: 303.14 \: kJ/kg$$
حال با مراجعه دوباره به جدول هوا، دمای متناظر با این مقدار آنتالپی را برابر $$\large T_2 \: = 303 \:K$$ مییابیم. نتیجه به دست آمده نشان میدهد که دمای هوا در حدود $$\large 20 \: ^\circ C$$ افزایش یافته، که این افزایش دما، ناشی از تبدیل انرژی جنبشی به انرژی درونی است.
مثال ۲
سؤال: بخار با فشار و دمایی به ترتیب برابر با $$\large 250 \:psia$$ و $$\large 700 \: ^\circ F$$ وارد نازل میشود. سطح مقطع ورودی نازل $$\large 0.2 \: ft^2$$ است. نرخ دبی جرمی بخار از داخل نازل را $$\large 10 \: lbm/s$$ در نظر بگیرید. بخار با فشار $$\large 200 \:psia$$ و سرعت $$\large 900 \: ft/s$$، نازل را ترک میکند. اتلاف گرما از نازل را در واحد جرم بخار، برابر با $$\large 1.2 \: Btu/ lbm$$ در نظر بگیرید. با توجه به این مقادیر، الف) سرعت ورودی، ب) دمای بخار در خروجی را به دست آورید.
پاسخ: حجم کنترل شکل زیر را در نظر بگیرید. پایستگی جرم و صفر بودن تغییرات انرژی پتانسیل، مانند مثال قبل برقرار است. تفاوت این مثال در انتقال حرارت است. در نتیجه، نمیتوانیم از سرعت ورودی صرف نظر کنیم.
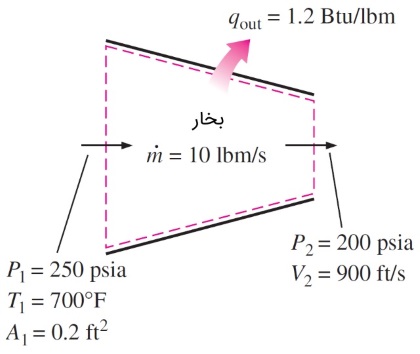
الف) با داشتن مقادیر زیر، سرعت ورودی به راحتی قابل محاسبه است.
$$\large \begin{cases} P_1 \:= 250 \:psia \\ T_1 \: = 700 \: ^\circ F\end{cases} ~~~ \Rightarrow ~~~ \begin{cases} v_1 \:= 2.6883 \: ft^3 / lbm \\ h_1 \: = 1371.4 \: Btu / lbm\end{cases} \\~\\
\large \dot{m} = \frac {1} {v_1} \times V_1 A_1 \\~\\
\large V_1 = \frac {(10 \: lbm/s) \times (2.6883 \: ft^3/lbm)} {0.2 \: ft^2} = 134.4 \: ft/s$$
ب) باز هم مانند مثال قبل، رابطه $$\large \dot{E}_{in} \: = \dot {E} _ {out}$$ برقرار است ولی با این تفاوت که بازنویسی این رابطه، به شکل زیر خواهد بود.
$$\large \dot{m} \: (h_1 + \frac {V^2_1} {2}) \: = \dot{Q} _ {out} \: +\dot {m} \: (h_2 + \frac {V^2_2} {2}) \\~\\
\large h_2 \: = h_1 \: - \: q_{out} - \: \frac {V^2_2 - V^2_1} {2} \\~\\
\large h_2 = (1371.4 \: - \: 1.2) Btu/lbm \: - \frac {(900 \: ft/s)^2 - (134.4 \: ft/s)^2} {2} (\frac {1 \: Btu/lbm} {25037 \: ft^2 / s^2}) \\~\\
\large h_2 \: = 1354.4 \: Btu/lbm \\~\\
\large \begin{cases} P_2 = 200 \: psia \\ h_2 \: = 1354.4 Btu/lbm \end{cases} ~~~ \Rightarrow ~~~ T_2 \: = 662 \: ^ \circ F$$
همانطور که مشاهده کردید، دمای بخار به اندازه $$\large 38 \: ^\circ F$$ کاهش یافت. این کاهش دما، به طور مستقیم از تبدیل انرژی درونی به انرژی جنبشی ناشی شده است. اتلاف گرما بسیار کم بوده و نمیتواند در این مورد، اثرگذار باشد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:
- فرآیند آدیاباتیک — به زبان ساده
- توربین فرانسیس (Francis Turbine) - از صفر تا صد
- عدد ماخ — به زبان ساده
^^









