تحلیل پوششی داده ها (DEA) – مفاهیم و کاربردها
تحلیل پوششی داده ها (Data Envelopment Analysis) که به اختصار به آن DEA نیز گفته میشود، یک روش ناپارامتری در حوزه تحقیق در عملیات و اقتصاد در نظر گرفته شده که کار آن اندازهگیری یا برآورد کارایی عملکرد واحدهای تولیدی است. البته در اینجا منظور از واحد تولیدی میتواند شامل کارخانجات و همینطور شرکتهای ارائه کننده خدمات نیز باشد. در نتیجه میتوان از تحلیل پوششی داده ها در هر نوع فعالیتی اقتصادی استفاده کرد و کارایی واحدهای تصمیمگیری در آن حوزه را بدست آورد. قرار است در این نوشتار به صورت مختصر، آشنایی با تحلیل پوششی داده ها (DEA) حاصل شده و از اصطلاحات آن آگاهی یابیم.
در بحث تحلیل پوششی داده ها (DEA) گاهی از مدل رگرسیونی نیز استفاده میشود در نتیجه بهتر است در مورد آن اطلاعاتی کسب کنید. بر همین اساس خواندن نوشتارهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده و رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده نیز پیشنهاد میشوند.
آشنایی با تحلیل پوششی داده ها (DEA)
در حوزه علم اقتصاد خرد و تولید، ترکیبهای ورودی (Input) و خروجی (Output) یک شرکت را میتوان به صورت یک تابع در نظر گرفت. چنین تابعی را گاهی «تابع تولید» (Production Function) مینامند. برای بدست آوردن بیشترین خروجی میتوان ترکیبهای مختلفی از مقادیر و متغیرهای ورودی را در نظر گرفت. به این ترتیب میتوانیم به یک تکنولوژی دست پیدا کنیم که شرکت یا کارخانه را به تولید بهینه برساند.
در سال ۱۹۵۷ ایده اولیه برای ایجاد تحلیل پوششی داده ها (DEA) توسط «فارل» (Farrel) مطرح شد و بعدها توسط «ابراهام چارنز» (Abraham Charnes)، «ویلیام کوپر» (William Cooper) و «ادوارد رودز» (Edward Rhodes) تئوری و محاسبات آن مورد استفاده قرار گرفت و امکان استفاده از چندین متغیر به عنوان ورودی و خروجی در تحلیل پوششی داده ها (DEA) بوجود آمد. به دلیل سادگی و موثر بودن شیوه تحلیلی در DEA، این تکنیک در بسیاری از موارد به منظور بررسی کارایی واحدهایی تولیدی یا خدماتی به کار گرفته میشود.
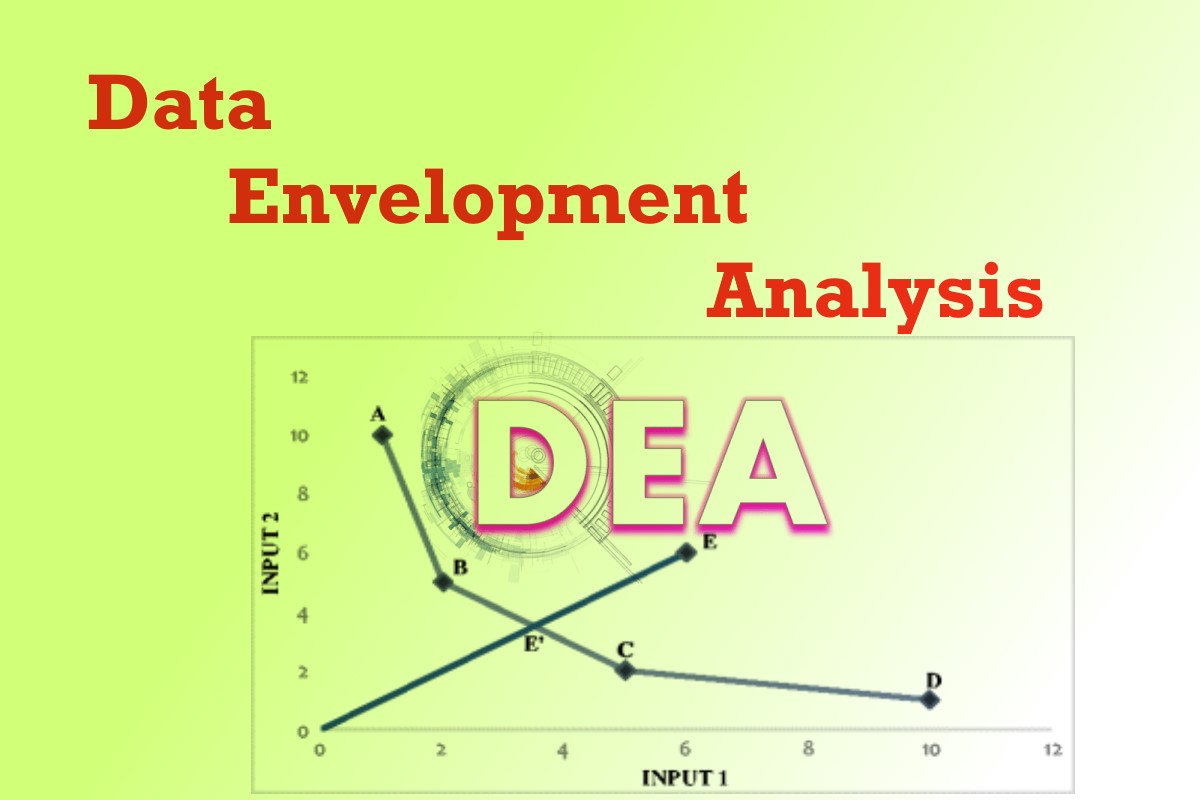
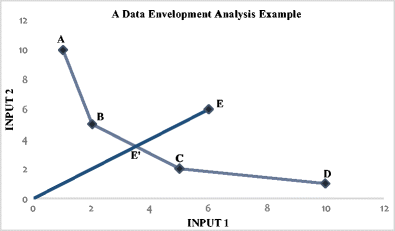
همانطور که در تصویر زیر مشاهده میکنید، مقادیر مربوط به ورودی و خروجی در بین چندین واحد مختلف اندازهگیری شده و نسبت آنها یا میزان بهرهوری محاسبه شده است. به این ترتیب بهرهوری براساس کسری محاسبه میشود که صورت آن خروجیها (ستاندهها) و مخرج نیز ورودیها (دادهها) است. پس میتوان کارایی یا بهرهوری را نسبت ستانده (Output) به داده (Input) در نظر گرفت. از آنجایی که همیشه مقدار داده بیشتر از ستانده است، کارایی یا بهرهوری مقداری کمتر از ۱ خواهد بود. این مقدار را گاهی به صورت درصدی نیز بیان میکنند.
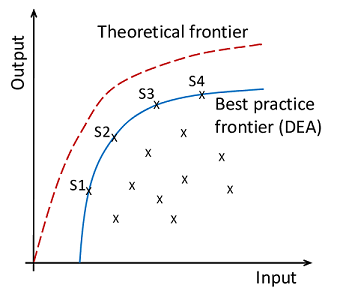
نقاط در این نمودار بیانگر واحدهای تصمیمگیری یا تولید هستند. به این ترتیب نقاطی از این نمودار که دارای بیشترین میزان بهرهوری هستند، شامل واحدهایی میشوند که در محور افقی کمترین ولی در محور عمودی بیشترین مقدار را دارند. در نتیجه مشخص است که واحدهای S1 تا S4 روی خط یا منحنیِ بهترین بهرهوری قرار دارند. چنین خط یا منحنی را بهترین خط یا منحنی «بهترین کارایی عملی» (Best Practice Frontier) مینامند. از طرفی ممکن است براساس استانداردها و محاسبات در فضای ایدهآل، مقدار بهرهوری برای هر یک از واحدها با مقدار واقعی متفاوت باشد. اتصال نقاط بهرهوری ایدهآل نیز منحنی به نام منحنی «کارایی تئوری» یا نظری (Theoretical Frontier) ایجاد میکند.
در حقیقت، DEA براساس برنامهریزی خطی (Linear Programming) عمل میکند و هدف آن بیشنیه سازی عملکرد است. پس میتوان آن را در گروه روشهای بهینهسازی خطی چند هدفه (چند خروجی) در نظر گرفت. برای مثال از DEA میتوان برای مقایسه کارایی «واحدهای تصمیمگیری» (Decision Making Units) یا DMU در یک شرکت استفاده کرد. همچنین از DEA برای اندازهگیری کارایی نسبی در بین صنایع مختلف یا شرکتها به منظور مقایسه آنها نیز میتوان بهرهبرداری نمود.
تحلیل پوششی داده ها دارای انواع مختلفی است؛ اصلیترین آن با نام روش CCR شناخته میشود که برگرفته از نام چارنز، کوپر و رودز است. شیوههای دیگر پیادهسازی DEA را با نامهای CRS یا «بازده به مقیاس ثابت» (Constant Return to Scale) و همچنین VRS یا «بازده به مقیاس متغیر» (Variable Return Scale) میشناسند.
تحلیل پوششی داده ها (DEA) چیست؟
همانطور که گفته شد، تحلیل پوششی داده ها براساس «برنامهریزی خطی» (Linear Programming) ایجاد شده است و ابزاری برای اندازهگیری و مقایسه کارایی چندین واحد تصمیمسازی (DMUs) محسوب میشود، بخصوص در زمانی که فرآیند تولید از یک ساختار ورودی و خروجی تشکیل شده باشد. تصویر زیر کاربرد DEA را در حوزههای مختلف تولیدی یا خدماتی بیان میکند.
مثالهایی از تحلیل پوششی داده ها (DEA)
کارایی یا بهرهوری (Efficiency) از دیدگاه کوپر و همکارانش از طریق مجموع وزنی خروجیهای یک فرآیند به ورودیهایش تعیین میشود. به این ترتیب مثالهایی زیر را در رابطه با نحوه عملکرد DEA میتوان مطرح کرد. فرض کنید دادههایی به صورت زیر موجود است:
- بخش ۱ از کارخانهای، تولیدی برابر با ۱۰۰ واحد در روز دارد. ورودیها که میتواند شامل مواد اولیه، انرژی، نفر بر ساعت باشد دارای هزینه هستند. هزینه مواد اولیه برای هر واحد تولیدی بالغ بر ۱۰ هزار تومان برآورد شده است. توجه داشته باشید که تولید هر محصول در این واحد به ۲ نفر-ساعت نیروی کار نیز احتیاج دارد.
- بخش ۲ از همین کارخانه نیز با تولید ۸۰ واحد، هزینه ورودی برابر با ۸ هزار تومان دارد که شامل مواد اولیه بوده و از لحاظ زمانی نیز ۴ نفر-ساعت را به خود اختصاص میدهد.
- بخش ۳ هم ۱۲۰ واحد تولید روزانه دارد که هزینه ورودیهای آن ۱۲ هزار تومان برای مواد و ۱٫۵ نفر-ساعت نیروی کار است.
بر اساس محاسبه کارایی یا بهرهوری بخش ۱ تابع هدف (Objective Function) که به اختصار OF نامیده میشود، را به صورت زیر تعریف میکنیم.
$$ \large OF\; :\; \max (\text{Efficiency}) = \dfrac{100 u_1}{(10 v_1 + 2 v_2)} $$
واضح است که مبنا را بخش ۱ در نظر گرفتهایم. از آنجایی که بهرهوری همیشه از ۱ کمتر است، قیدهای زیر را هم در نظر میگیریم.
- کارایی بخش ۱ کمتر از ۱: $$ {\displaystyle \dfrac{(100 u_{1})}{(10 v_{1} + 2 v_{2})} \leq 1} $$
- کارایی بخش ۲ کمتر از 1: $$ {\displaystyle \dfrac{(80u_{1}) }{ (8 v_{1} + 4 v_{2})} \leq 1}$$
- کارایی بخش ۳ کمتر از ۱: $$ {\displaystyle \dfrac{(120u_{1})}{(12v_{1} + 1.5v_{2})} \leq 1} $$
- نامنفی بودن پارامترها: هیچ یک از $$u$$ یا $$v$$ها منفی نیستند. $$ u , v \geq 0$$
نکته: گاهی قیدها (Such That) را به صورت مخفف و با ST نشان میدهند.
از آنجایی که پارامترهای مورد نظر برای تصمیمگیری ($$v_1 , v_2 , u_1$$) هم در صورت و هم در مخرج قرار دارند، مدل به صورت غیرخطی خواهد بود. ولی چون میخواهیم از یک مدل برنامهریزی خطی استفاده کنیم باید بوسیله فرمولهای خطی سازی (Linearize)، تابع هدف و شرطها را به شکل دلخواه درآوریم، بطوری که مخرج کسر تابع هدف ثابت (مثلا در اینجا برابر با ۱) شود و سپس فقط کافی است که به کمک روشهای برنامهریزی خطی، تابع هدف جدید را بیشنیه کنیم.
به این ترتیب تابع هدف (OF) را به صورت زیر بازنویسی میکنیم (در اینجا مخرج را برابر با ۱ قرار دادهایم).
$$ \large \max (\text{Efficiency}) = 100 u_1 $$
و در نتیجه قیدها نیز به شکل زیر درخواهند آمد.
- کارایی بخش ۱ کمتر از صفر: $$ \text{ST1}: {\displaystyle 100 u_{1} -(10 v_{1} + 2 v_{2}) \leq 0} $$
- کارایی بخش ۲ کمتر از صفر: $$ \text{ST2}: {\displaystyle (80u_{1})- (8 v_{1} + 4 v_{2}) \leq 0}$$
- کارایی بخش ۳ کمتر از صفر: $$ \text{ST3}:{\displaystyle (120u_{1})- (12v_{1} + 1.5v_{2}) \leq 0} $$
- شرط مربوط به مخرج تابع هدف غیر خطی: $$ \text{ST4}:{\displaystyle (10 v_{1} + 2 v_{2}) = 1} $$
- نامنفی بودن پارامترها: هیچ یک از $$u$$ یا $$v$$ها منفی نیستند. $$ u , v \geq 0$$
حال به کمک روشهای برنامهریزی خطی، مقدار بیشینه تابع هدف را با توجه به قیدهای ذکر شده بدست میآوریم.
کاربردهای تحلیل پوششی داده ها (DEA)
همانطور که گفته شد، هر زمان احتیاج به مقایسه کارایی وجود داشته باشد، میتوان از DEA استفاده کرد. برای مثال، نهادهای نظارتی دولتی از DEA برای تعیین حدود استاندارد کارایی شرکتها و صنایع به صورت مقایسهای استفاده میکنند. به این ترتیب تعداد افراد به کار گرفته شده (شاغل)، سود (زیان)، سرمایه (اصلی و در گردش) و میزان تولید به عنوان ورودی در نظر گرفته شده و تعداد مشتریان، انرژی انتقال داده شده و طول عمر محصول به عنوان خروجی به کار میروند. به تازگی از تحلیل پوششی داده ها (DEA)، برای اندازه گیری کارایی «نهادهای غیر انتفاعی» (Not for Profit Organizations) مانند بیمارستانهای دولتی یا «سازمانهای مردم نهاد» (Non- Governmental Organization) نیز استفاده میشود.
در قسمت قبل دیدیم که در شیوهای که چارنز پیشنهاد کرد، کارایی (Efficiency) به صورت نسبت مجموع وزنی خروجیها به مجموع وزن ورودیها اندازهگیری میشود. تعیین وزنها نیز به کمک روشهای برنامهریزی ریاضی (Mathematical Programming) انجام میشود.
در ادامه به عملیاتی که توسط DEA انجام میگیرد، آشنا میشوید:
- در DEA، واحدهای خدماتی با توجه به منابعی و نوع خدماتی که مصرف و تولید میکنند، با یکدیگر مقایسه میشوند. واحد با بیشترین کارایی در این قسمت (بخش، دپارتمان، کارکنان) شناسایی شده واحدهایی با کارایی ضعیف مشخص شده و میزان کارایی ایدهال (عملی) چنین واحدهایی نیز مشخص میشود. به این ترتیب میتوان به کمک DEA، ابزاری برای مقایسه راندمان بخشها یا فعالیتهای شرکتها یا سازمانها ایجاد کرد.
- تعداد و نوع منابع صرفهجویی شده در اثر بهرهوری بیشتر هر DMU با تکنیک تحلیل پوششی داده ها (DEA) اندازهگیری شده به این ترتیب واحدهای ناکارآمد تشویق به کارآمدی میشوند یا به کمک سیاستهایی، بهرهوری آنها بهبود مییابد.
- از آنجایی که میزان ناکارآمدی واحدهای با بهرهوری پایین اندازهگیری شده است، مدیریت میتواند با بهینهسازی آنها میزان صرفهجویی مالی را اندازهگیری کند. حتی به کمک DEA مدیران میتوانند DMUهایی که کارایی دارند را فعالتر کرده و بهرهوری آنها را بدون اضافه کردن ورودی (منابع جدید) بهبود دهند.
- با دریافت اطلاعات از کارایی بخشهای تولیدی و خدماتی، مدیریت میتواند به قابلیتهای خود، بخصوص در امر تصمیمگیری، بیافزاید و سازمان را به سوی تعالی سوق دهد.
مزایا و معیاب تحلیل پوششی داده ها (DEA)
هر چند شیوه DEA کاربردی و البته کارا است ولی بعضی از مشکلات ناشی از به کارگیری آن در مقایسههای مربوطه بوجود میآید که در ادامه علاوه بر مزایا به معایب آن هم اشاره خواهیم کرد.
مزایا
- در تکنیک DEA، احتیاجی به بیان فرم ریاضی ارتباط بین ورودی و خروجیها وجود ندارد و ارتباط براساس خود مقادیر ورودی و خروجی تعیین میشود. همین امر آن را به عنوان یک روش ناپارامتری طبقهبندی میکند.
- استفاده از DEA، ممکن است ارتباطات جدیدی را مدلبندی کند که در شیوههای دیگر کشف نشده و مخفی ماندهاند.
- امکان به کارگیری همزمان چندین ورودی و خروجی در تحلیل پوششی داده ها وجود دارد.
- انواع ورودی و خروجیها را میتوان در تحلیل پوششی داده ها (DEA) به کار گرفت.
- منابع تاثیرگذار در ناکارآمدی سازمانها به واسطه به کارگیری DEA، تجزیه و تحلیل میشود.
معایب
- نتایج حاصل از تحلیل پوششی داده ها به انتخاب ورودی و خروجی ها بسیار وابسته است. در نتیجه انتخاب نامناسب هر یک از آنها، نتایج حاصل را تحت تاثیر قرار داده و منحرف میکند.
- متاسفانه با افزایش تعداد ورودی و خروجیها میزان کارایی شرکتها و صنایع براساس تحلیل پوششی داده ها (DEA) افزایش یافته بدون آنکه برایش توضیح قابل قبولی وجود داشته باشد.
ناکارآمدی تحلیل پوششی داده ها
تحلیل پوششی داده ها (DEA) به منظور تحلیل کارایی بخصوص به عنوان ابزاری کاربردی در «سیستمهای حامی تصمیم» (Decision Support Systems) یا DSS به کار میرود. هر چند تحلیل پوششی داده ها (DEA) نیازی به نوشتن فرم صریح تابع تولید ندارد ولی نیازمند کلیاتی از نحوه تولید و توزیع آن است. اگر شرطهای در نظر گرفته شده ضعیف بوده یا به درستی تنظیم نشده باشند، به طور خودکار، DEA دچار کمبرآوردی (Underestimation) و همچنین اریبی (Biased) در نتایج خواهد شد. در نتیجه بهتر است برای تعیین شرطها و همچنین تابع هدف دقت کافی را به کار برد.
خلاصه و جمعبندی
در این نوشتار با تحلیل پوششی داده ها (DEA) آشنا شدیم. همچنین مثالهایی نیز از کارکرد این تکنیک در حوزه صنایع و تولید مورد بررسی قرار گرفت. از آنجایی که محاسبات مربوط به روش DEA تماما به خود دادهها وابستگی دارد آن را به عنوان یک روش ناپارامتری در رده برنامهریزی خطی در نظر میگیرند.








سلام
نخست پوزش می خواهم که پرسش من خیلی ابتذایی است.
به نظر می رسد آنچه شمادر تحلیل پوششی داده ها اندازه گیری می کنید یعنی نسبت خروی ها به ورودی ها بهره وریست نه کارایی به معنی راندمان وقاعدتا مقدار آن باید بیشتر از 1 یاشد نه کمتر است 1 زیرا کمتر از 1 بودن آن به معنی زیان ده بودن شرکت است. اگر قرار باشد خروجی های سک شرکت همواره کمتر از ورودی های آن باسشد چرا فعالیت می کند. ظاهرا آنچه شما ماکزیمایز می کنید به عددی کمتذ از یک باید مینیمایز شئد به عددی بزرگتر از یک.
راندمان همیشه کمتر یا مساوی 1در حتالت ایدال و بهره وی همواره یلید بزرگتر از 1 باشد تا فعالیت اقتصادی معنی دار باشد.
سلام .
من میخواهم از این بحث در قسمتی از پروپوزال خود استفاده کنم . امکان انتخاب برای منبع است .
چگونه دانلود کنم این متن را؟
با سلام؛
برای استفاده از مطالب «مجله فرادرس» میتوانید «شرایط استفاده» را در اینجا یا در انتهای صفحات مجله مطالعه کنید.
با تشکر از همراهی شما با مجله فرادرس