مدار الکتریکی چیست؟ – آشنایی با انواع مدار به زبان ساده
تمام وسایل برقی که در اطراف خود مشاهده میکنید، از یک یا چند مدار الکتریکی تشکیل میشوند. مدار الکتریکی از اتصال چند عنصر الکتریکی مهم مانند باتری، لامپ، سیم رسانا و ... به یکدیگر ساخته میشود. در این مطلب از مجله فرادرس قصد داریم ببینیم مدار الکتریکی چیست و با مفاهیم اساسی حاکم بر مدارات الکتریکی مانند ولتاژ و جریان آشنا شویم، قواعد حاکم بر عملکرد مدار الکتریکی را بررسی کنیم و کاربردهای آن را بهتر درک کنیم.
- یاد میگیرید که مفاهیم بنیادی مدار الکتریکی را بهدرستی تعریف کنید.
- نقش و عملکرد عناصر کلیدی مانند مقاومت، خازن، سلف و منابع را خواهید آموخت.
- میآموزید چگونه مفهوم ولتاژ، جریان، اختلاف پتانسیل و نیرو محرکه را تحلیل کنید.
- تفاوت ساختاری و تحلیلی منابع مستقل و وابسته را یاد خواهید گرفت.
- کاربرد اصولی قوانین کیرشهف و روشهای تحلیل گره و مش را خواهید شناخت.
- تشخیص و تحلیل مدارهای مرتبه اول و دوم با مدلسازی معادلات دیفرانسیل را میآموزید.


مهم ترین کمیت ها در یک مدار الکتریکی چه هستند ؟
پیش از بررسی اجزای یک مدار الکتریکی، قصد داریم تا با کمیتهای اساسی در آنها آشنا شویم. شناخت این کمیتها باعث میشود که بتوانیم آنالیز بهتری در خصوص یک مدار الکتریکی داشته باشیم. علاوهبر کمیتهای مهم، اجزای مهم مدار الکتریکی را داریم که عبارتاند از باتری، کلید، سیم رسانا، مقاومت، خازن، دیود و ...
بار الکتریکی در مدار الکتریکی چیست ؟
هر ماده، ویژگیهایی دارد که با وجود آنها خواصی را پیدا میکند. «جرم» (Mass)، «اسپین مغناطیس» (Magnetic Spin) و... از جمله ویژگیهای یک ماده هستند. «بار الکتریکی» (Electric Charge) نیز یکی از این ویژگیها است. به عنوان مثال، هرگز مادهای یافت نمیشود که فاقد بار الکتریکی باشد. البته ممکن است مادهای از نظر الکتریکی خنثی باشد؛ اما به این معنی نیست که بار الکتریکی ندارد. بلکه مجموعه بارهای مثبت و منفی در آنها با یکدیگر برابر است.
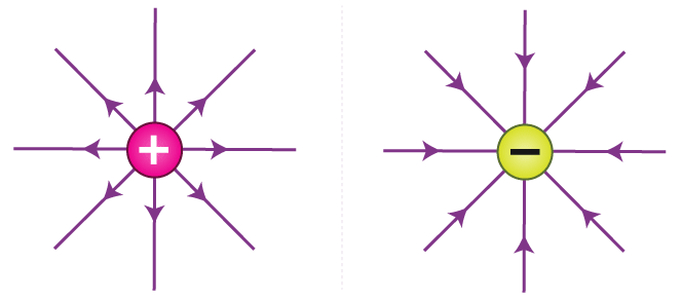
بار الکتریکی، خاصیتی از ماده است. این خاصیت سبب میشود زمانی که یک ماده در مجاورت یک ماده باردار دیگر قرار میگیرد، به آن نیرو وارد شود. به طور کلی دو نوع بار الکتریکی وجود دارد که توسط دانشمند و سیاستمدار آمریکایی یعنی «بنجامین فرانکلین» (Benjamin Franklin) به صورت بار مثبت و منفی نامیده شد. این نامها توسط فرانکلین به شکل دلخواه انتخاب شدند.
نیرو محرکه الکتریکی در مدار چیست ؟
یکی از عوامل اساسی در عملکرد یک مدار الکتریکی، وجود اختلاف پتانسیل در آن است تا به سبب آن، جریان الکتریکی برقرار شود. این اختلاف پتانسیل میتواند توسط ابزاری مانند باتریها در مدار ایجاد شود. نیرویی که در داخل این ابزار سبب میشود تا این اختلاف پتانسیل در دو سر آنها ایجاد شود، «نیرو محرکه الکتریکی» (Electromotive Force) نام دارد.
در واقع، نیرو محرکه الکتریکی میزان نیرویی است که توسط باتری به بارهای الکتریکی وارد میشود تا به واسطه این نیرو، بارهای الکتریکی به حرکت دربیایند و جریان الکتریکی در مدار برقرار شود. لازم به ذکر است که نیرو محرکه الکتریکی از جنس نیرو نیست و لفظ نیرو صرفا برای نامگذاری آن به کاربرده شده است؛ زیرا این کمیت نه بر حسب نیوتن، بلکه بر حسب ولت بیان میشود.
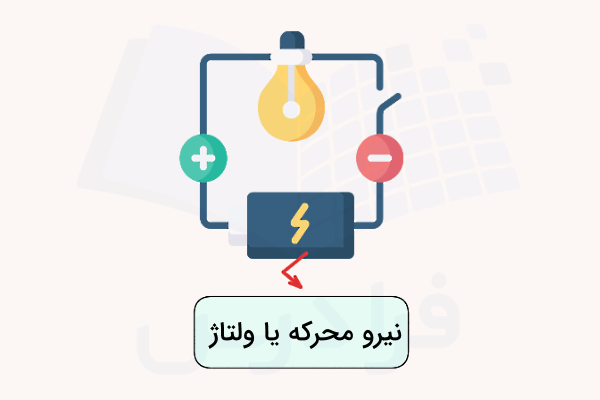
بهمنظور نشان دادن نیرو محرکه الکتریکی از نماد «ε» استفاده میشود. باتریها و «سلولهای خورشیدی» (Solar Cells) نمونههای بارزی از این کمیت هستند. در حقیقت نیرو محرکه الکتریکی، پمپ الکتریکی است که بارها را از پتانسیل کمتر به پتانسیل بیشتر منتقل میکند. از نظر ریاضیاتی نیروی محرکه به صورت زیر تعریف میشود.
جریان در مدار الکتریکی چیست ؟
در نگاه اولیه، یک مدار الکتریکی ساده از منبع، سیم و مصرفکننده تشکیل شده است. زمانی که در دو سر منبع موجود در مدار، اختلاف پتانسیل به وجود میآید، بارهای الکتریکی شروع به حرکت میکنند. این حرکت به این شکل است که هنگام ایجاد اختلاف پتانسیل توسط منبع، بارها در داخل منبع از پلاریته منفی به پلاریته مثبت حرکت میکنند و از پلاریته مثبت منبع خارج میشود. در طول مدار حاملهای بار مثبت از طریق سیمها جاری میشوند و به سمت پلاریته منفی منبع، حرکت میکنند.
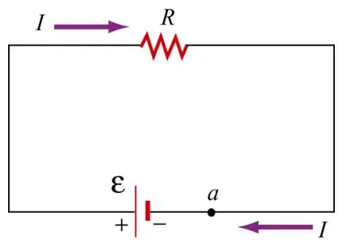
برخلاف تصور بسیاری از افراد، جریان الکتریکی با حرکت بارهای الکتریکی به وجود نمیآید، بلکه این شارش بارهای الکتریکی است که جریان الکتریکی را ایجاد میکند. در اینجا نیز منظور از حرکت الکترونها در طول سیم، شارش است. به عبارتی، الکترونها در تمامی بخشهای یک سیم رسانا وجود دارند و اینگونه نیست که بار الکتریکی در داخل سیم بخواهد به سمت نقطهای حرکت کند که فاقد بار است. درست مانند زنجیری که به یک قرقره متصل شده است و با چرخش قرقره، این زنجیر حرکت میکند. بنابراین، جریان الکتریکی نرخ شارش بارهای الکتریکی است که این تعریف توسط معادلات ریاضی، به شکل زیر بیان میشود:
در عمل منظور از حرکت بارهای الکتریکی حرکت الکترونها است. اگر بخواهیم جریان الکتریکی را بر حسب حرکت الکترونها مورد بررسی قرار دهیم، باید بگوییم که الکترونها از پلاریته منفی منبع، جاری شده و به سمت پلاریته مثبت منبع، شارش میکنند. اما در بسیاری از مواقع، به این شکل قرارداد میشود که جریان از سر مثبت منبع خارج شده و در طول مدار به طرف سر منفی آن میرود. شارش الکترونها در داخل سیم رسانا به این صورت است که با «حرکات کاتورهای» (Random Motions) یا «حرکات براونی» (Brownian Motion) و نامنظم و با ضربه زدن به یکدیگر سبب ایجاد جریان در مدار الکتریکی میشوند. شکل زیر حرکات کاتورهای الکترونها در داخل یک سیم رسانا را نشان میدهد.
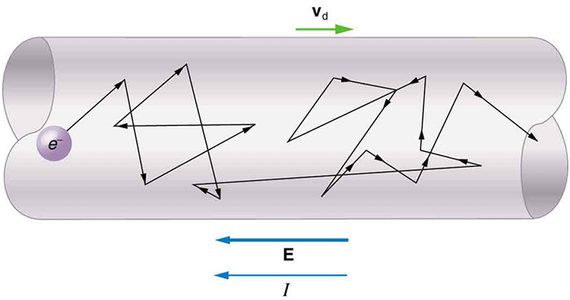
شما میتوانید بسیاری از مفاهیم و نرمافزارهای کاربردی حوزه مدار الکتریکی را با استفاده از فیلمهای مجموعه آموزش طراحی مدارات الکتریکی و الکترونیکی – مقدماتی تا پیشرفته در فرادرس یاد بگیرید.
توان در مدار الکتریکی چیست ؟
هنگام تحلیل مدارهای الکتریکی معمولا جریان یک شاخه یا ولتاژ یک گره در مدار را محاسبه میکنیم. در حقیقت، منظور از آنالیز یک مدار الکتریکی محاسبه ولتاژ یا جریان محدوده مشخصی از آن است. اما در عمل، آن کمیتی که مورد استفاده قرار میگیرد «توان الکتریکی» (Electric Power) و انرژی الکتریکی است. البته هنگام پیادهسازی یک مدار الکتریکی در عمل، ولتاژ و جریان در نقاط مختلف آن توسط ولتمتر و آمپرمتر قابل اندازهگیری هستند. اما آن چیزی که به صورت واقعی تولید و مصرف میشود، توان الکتریکی است. یک مطلب اساسی فیزیک این است که توان لحظهای تولید شده توسط یک منبع، برابر است با ولتاژ لحظهای دو سر آن منبع، در جریان لحظهای گذرنده از آن، به شرطی که جهتهای قراردادی متناظر در آن رعایت شده باشند.
تفاوت ولتاژ، اختلاف پتانسیل و نیرو محرکه الکتریکی در مدار چیست ؟
ولتاژ، اختلاف پتانسیل و نیرو محرکه الکتریکی، مفاهیمی هستند که به طور کلی به یک رخداد یکسان اشاره میکنند. در واقع، وجود هر یک از این مفاهیم سبب میشود که جریان الکتریکی به وجود آمده و مدار شروع به کار کند. اما اگر بخواهیم به طور دقیق این سه را با یکدیگر مقایسه کنیم، خواهیم دید که با یکدیگر تفاوتهایی نیز دارند.
عاملی که سبب ایجاد جریان الکتریکی در مدار میشود، اختلاف پتانسیل است. زمانی که یک عنصر در مدار، اختلاف پتانسیل ایجاد میکند، در دو سر این عنصر، ولتاژ به وجود میآید. حال عاملی که در ابتدا سبب میشود که اختلاف پتانسیل توسط عنصر مربوطه ایجاد شود، نیرو محرکه الکتریکی است. بنابراین نیرو محرکه الکتریکی باعث به وجود آمدن اختلاف پتانسیل شده و وجود اختلاف پتانسیل سبب به وجود آمدن ولتاژ در نقاط مشخص میشود.
مدارهای فشرده و قوانین کیرشهف
در این بخش، به معرفی مدارهای فشرده و قوانین کیرشهف میپردازیم.
مدارهای فشرده چه هستند؟
در نگاه اول ممکن است اینگونه به نظر برسد که قوانین کیرشهف در خصوص تمامی مدارهای الکتریکی به کار میروند. اما در عمل با چیزی غیر از این مواجه میشویم. آزمایشات مختلف نشان میدهند که این قوانین تنها در خصوص مدارهایی به کار میروند که ویژگیهای خاصی داشته باشند. شناخت این ویژگیها سبب میشوند که در مواجه با یک مدار الکتریکی بدانیم که آیا میتوانیم از قوانین کیرشهف جهت تحلیل مدار استفاده کنیم یا خیر.
به طور کلی میدانیم که فرکانس با طول موج رابطه معکوس دارد. به عبارتی، هر چقدر فرکانس کاری یک سیستم بالاتر برود، طول موج پایین میآید و هر چقدر این طول موج بالاتر باشد اثرات الکترومغناطیسی در مدار، کمتر مشاهده میشود. به عنوان مثال، در یک سیستم قدرت فرکانس در حدود ۵۰ هرتز یا ۶۰ هرتز است. طول موج متناسب با فرکانس ۵۰ هرتز در حدود ۶۰۰۰ کیلومتر است. این طول موج به قدری بزرگ است که فاصله چند صد کیلومتری نیروگاه تا مصرفکننده در مقابل آن ناچیز است و عملا به چشم نمیآید. زمانی که سیستم در چنین شرایطی قرار دارد، میتوانیم بگوییم که هر رفتاری که مدار در بخش تولید یا نیروگاه دارد، همان رفتار در بخش مصرفکننده که در فاصله چند صد کیلومتری در آن قرار دارد نیز مشاهده میشود.

حال مداری را در نظر بگیرید که در فرکانس ۱ گیگاهرتز کار میکند. طول موج متناسب با این فرکانس در حدود ۳۰ سانتیمتر است. حال اگر ابعاد چنین مداری در حدود ۲۰ سانتیمتر باشد، رفتار مدار در ابتدا و انتهای آن با هم متفاوت است؛ زیرا طول موج، سبب تغییر رفتار مدار در نقاط مختلف آن میشود و ۲۰ سانتیمتر در مقابل ۳۰ سانتیمتر قابل چشمپوشی نیست. مداری که بتوان از ابعاد آن در مقابل طول موج متناظر صرف نظر کرد، «مدار فشرده» (Lumped Circuit) نام دارد. مادامی که این محدودیت اندازه مدار برقرار باشد، قوانین جریان و ولتاژ کیرشهف معتبر خواهند بود. مداری که فشرده نباشد، «مدار گسترده» (Distributed Circuit) نام دارد. در تحلیل مدارات گسترده، به علت وجود اثرات قابل توجه الکترومغناطیسی، قوانین بنیادی کیرشهف معتبر نیستند.
مفاهیم اساسی در مدار الکتریکی چه هستند ؟
پیش از آنکه بخواهیم اجزای یک مدار الکتریکی را بررسی کنیم، ابتدا با چند مفهوم ساده آشنا میشویم. به عنوان مثال مدار الکتریکی زیر را در نظر بگیرید.
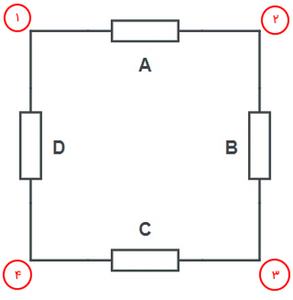
- المانهای C ،B ،A و D عناصر مدار نامیده میشوند که میتوانند مقاومت، خازن، سلف یا ترانسفورماتور باشند.
- نقاط ۱، ۲، ۳ و ۴، گره، باس یا شین نامیده میشوند.
- خطوطی که بین نقاط ۲-۱، ۳-۲، ۴-۳ و ۴-۱ قرار دارند، شاخه (فیدر، هادی یا خط) نامیده میشوند.
جهت های قراردادی در مدارهای الکتریکی چه هستند؟
یک المان مداری به صورت زیر را در نظر بگیرید. این المان میتواند مقاومت، خازن یا سلف باشد.

طبق یک قرارداد کلی، جریان i را در شرایطی یک جریان مثبت در نظر میگیریم، اگر از پتانسیل بیشتر به پتانسیل کمتر جاری شود. شارش جریان از یک پتانسیل بیشتر به کمتر، بدین معنی است که مقدار ولتاژ در نقطه A از مقدار ولتاژ در نقطه B بیشتر است. در حقیقت اگر بخواهیم در آنالیز یک مدار الکتریکی، جهتهای قراردادی را رعایت کنیم، در صورت امکان، جهت جریان را طوری انتخاب میکنیم که از سر مثبت عنصر وارد آن شود.
البته جهتهای قراردادی متناظر، قوانین ثابت و نامتغیری نیستند و همانطور که از نام آنها پیداست یک قرارداد محسوب میشوند و میتوان در تحلیل یک مدار عکس این جهت را به عنوان جهت قراردادی معین نمود؛ زیرا این موضوع صرفا جنبه تئوری داشته و تاثیری در عملکرد فیزیکی مدار و آنچه در ساختار داخلی آن رخ میدهد ندارد. اما رعایت کردن جهتهای قراردادی متناظر، نظم خوبی را در روند تحلیل مدار الکتریکی ایجاد میکنند.
قوانین بنیادی گوستاو کیرشهف
«گوستاو روبرت کیرشهف» (Gustav Robert Kirchhoff)، فیزیکدان آلمانی، در سال ۱۸۲۴ میلادی (۱۲۳۹ شمسی) در کونیگسبرگ، پروس به دنیا آمد. اولین موضوع تحقیق او هدایت الکتریسیته بود. این تحقیقات منجر به تدوین قوانین مدارهای الکتریکی بسته توسط کیرشهوف در سال ۱۸۴۵ میلادی (۱۲۶۰ شمسی) شد. این قوانین در نهایت به نام کیرشهف نامگذاری شدند و اکنون به عنوان قوانین ولتاژ و جریان کیرشهف شناخته می شوند. از آنجایی که این قوانین برای همه مدارهای الکتریکی فشرده اعمال می شوند، درک اصول آنها در درک نحوه عملکرد یک مدار الکترونیکی بسیار مهم است. اگرچه این قوانین، کیرشهوف را در مهندسی برق جاودانه کرده است، اما او اکتشافات دیگری نیز دارد. به عنوان مثال، او اولین کسی بود که تایید کرد که یک تکانه الکتریکی با سرعت نور حرکت می کند. علاوه بر این، کیرشهف سهم عمده ای در مطالعات طیف سنجی داشت.

قانون جریان کیرشهف در مدار الکتریکی چیست ؟
در حالت کلی، «قانون جریان کیرشهف» (Kirchhoff Current Law) بیان میکند که: «در هر گره از هر مدار الکتریکی فشرده و در هر لحظه از زمان، مجموع جبری جریان همه شاخههایی که از آن گره خارج میشوند، برابر صفر است». این قانون به اصطلاح «قانون اول کیرشهف» یا به اختصار «KCL» نیز نامیده میشود. هنگامی که بخواهیم این قانون را برای بررسی در یک گره خاص به کار ببریم، ابتدا برای جریانهای ورودی و خروجی، علامتی را قرارداد میکنیم. در واقع، اهمیتی ندارد که علامت مثبت یا منفی را برای کدام جهت جریان در نظر میگیریم. موضوعی که اهمیت دارد این است که هرچه قرارداد کردهایم را تا پایان محاسبات مربوط به مدار مورد نظر، ثابت نگه داریم. به عنوان مثال اگر جریانهای ورودی به گره را با علامت مثبت، و جریانهای خروجی از گره را با علامت منفی در نظر میگیریم، این جهت قراردادی باید تا پایان محاسبات مربوط به مدار مورد نظر ثابت بماند. در شکل زیر معادله KCL برای یه گره مشخص با پنج شاخه نوشته شده است.
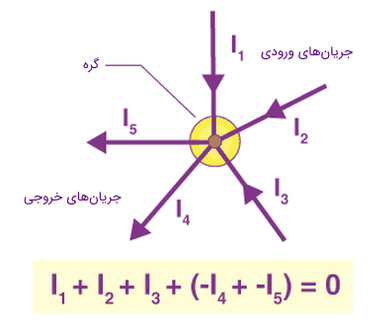
در شکل فوق، جریانهای ۱ و ۲ و ۳ جریانهایی هستند که به گره مورد نظر وارد میشوند که در این گره، جریانهای واردشونده با علامت مثبت در نظر گرفته میشوند. همچنین جریانهای ۴ و ۵ از گره مورد نظر خارج میشوند که در این گره، جریانهای خارجشونده با علامت منفی در نظر گرفته شدهاند. هنگامی که علامتها به این شکل قرارداد میشوند، تا انتهای آنالیز مدار مورد نظر، باید جریانهای واردشونده با علامت مثبت و جریانهای خارجشونده با علامت منفی در نظر گرفته شوند و در تمامی گرههای مدار نیز اعمال شوند.
قانون KCL در مورد هر مدار الکتریکی فشرده به کار میرود. در واقع اینکه عناصر مدار الکتریکی، خطی، غیرخطی، تغییرپذیر با زمان، تغییرناپذیر با زمان و غیره باشند اهمیتی در کاربرد این قانون ندارد. به عبارت دیگر، قانون KCL به ماهیت اجزای مدار بستگی ندارد.
- نکته: قانون KCL نه تنها در هر گره ساده، بلکه در هر گره مرکب نیز برقرار است. گره مرکب گرهای است که با در نظر گرفتن دو یا چند گره با هم به عنوان یک گره حاصل میشود. بدیهی است، شاخههایی که در داخل گره مرکب قرار میگیرند، در نوشتن معادله KCL در آن گره مرکب نقشی ندارند.
قانون ولتاژ کیرشهف در مدار الکتریکی چیست ؟
در حالت کلی، «قانون ولتاژ کیرشهف» (Kirchhoff Voltage Law) بیان میکند که: «در هر حلقه از هر مدار الکتریکی فشرده و در هر لحظه از زمان، مجموع جبری ولتاژهای شاخههای حلقه برابر صفر است». این قانون به اصطلاح «قانون دوم کیرشهف» یا به اختصار «KVL» نیز نامیده میشود. هنگامی که بخواهیم این قانون را برای یک حلقه خاص به کار ببریم باید یک جهت قراردادی برای حلقه تعیین کنیم. در قانون ولتاژ کیرشهف نیز همانند قانون جریان یا KCL، اهمیتی ندارد که در چه جهتی (ساعتگرد یا پادساعتگرد) درون حلقه مورد نظر حرکت کنیم. اما هنگام عبور از هر المان با ولتاژ مشخص، باید پلاریته ولتاژ را ثابت نگه داریم. در شکل زیر معادله KVL برای یک حلقه مشخص با چهار المان مداری نوشته شده است.
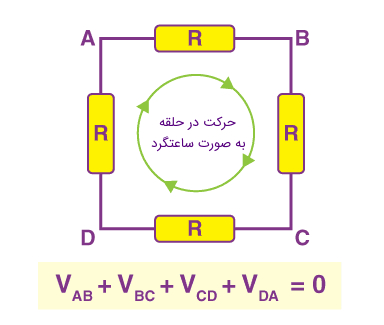
در شکل فوق، به در جهت حرکت عقربههای ساعت در حلقه حرکت میکنیم و در مواجه با هر یک از المانها، ولتاژ دو سر آنرا مینویسیم. در مجموع، هنگام نوشتن معادله KVL، ولتاژ شاخههایی را که جهت قراردادی آنها با جهت قراردادی حلقه، یکی است، با علامت مثبت و ولتاژ شاخههایی را که جهت قراردادی آنها با جهت قراردادی حلقه یکی نیست با علامت منفی در نظر میگیریم. در خصوص این قانون نیز میتوان گفت که KVL در مورد هر مدار الکتریکی فشرده به کار میرود. در واقع اینکه عناصر مدار الکتریکی، خطی، غیرخطی، تغییرپذیر با زمان، تغییرناپذیر با زمان و غیره باشند اهمیتی در کاربرد این قانون ندارد. به عبارت دیگر، قانون KVL به ماهیت اجزای مدار بستگی ندارد.
اجزای مدار الکتریکی چه هستند ؟
در این قسمت قصد داریم عناصری که به طور معمول در ساختار مدارهای الکتریکی مورد استفاده قرار میگیرند را بررسی کنیم. این عناصر عبارتند از: مقاومت، منابع ولتاژ و جریان، خازن، سلف و غیره. البته در این مقاله، عملکرد عناصر نامبرده شده در شرایط عادی و نرمال بررسی میشوند.
به عنوان مثال، زمانی که فرکانسی که مدار در آن کار میکند، از حدی بالاتر رود عملکرد این المانها متفاوت خواهد بود. در واقع، زمانی که فرکانس کاری یک مدار الکتریکی از مقدار مشخصی بالاتر میرود، سعی بر این است که تا حد امکان از عناصری نظیر خازن و سلف به جای مقاومتها استفاده شود؛ زیرا مقاومتها یکی از منابع نویز به شمار میآیند. به همین خاطر، با بالا رفتن فرکانس، اثرات نویز مقاومتها به طور چشمگیری افزایش مییابد. در حالی که در شرایط عادی چنین رفتاری از یک مقاومت مشاهده نمیشود.
مقاومت در مدار الکتریکی چیست ؟
از دیدگاه ریاضی، مقاومت المانی است که بتوان ولتاژ موجود در دو سر آن و جریان گذرنده از آنرا در هر لحظه از زمان با یک منحنی نشان داد. این منحنی، «مشخصه مقاومت» (Resistor Characteristic) نام دارد. نکته قابل توجه این است که مشخصه نامبرده، الزاما یک تابع نیست به همین علت از نام مشخصه بهجای تابع استفاده شده است. در حقیقت بسته به پدیدههای فیزیکی که در داخل عنصر مورد نظر رخ میدهد، این مشخصه متفاوت است. در شکل زیر مشخصه یک مقاومت خطی تغییرناپذیر با زمان را مشاهده میکنید.
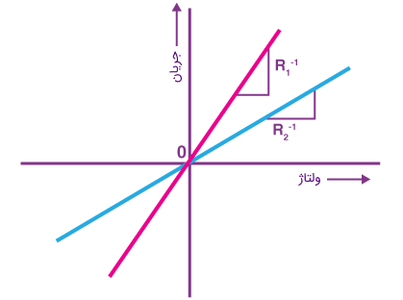
از یک دیدگاه مقاومتها میتوانند «خطی» (Linear) یا «غیرخطی» (Nonlinear) باشند. مقاومتی خطی است که مشخصه آن خط مستقیمی در صفحه v-i باشد که از مبدا مختصات میگذرد. به همین ترتیب مقاومتی غیرخطی است که خطی نباشد. یعنی یا خط مستقیمی نباشد، یا ممکن است مشخصه آن خط مستقیمی باشد اما این مشخصه از مبدا مختصات عبور نکند. امروزه از مقاومتهای غیرخطی بسیار زیادی در الکترونیک استفاده میشود. به عنوان مثال، شکل زیر مشخصه یک مقاومت غیرخطی را نشان میدهد.
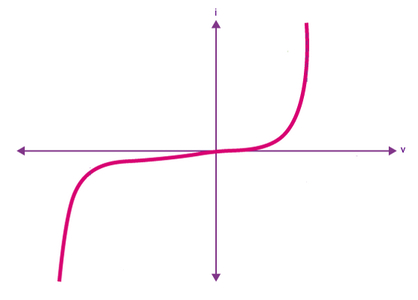
همانطور که در شکل فوق مشاهده میکنید، مشخصه رسم شده در صفحه v-i از مبدا مختصات عبور کرده است اما خط مستقیمی نیست و در ربع اول، به شکل نمایی ادامه پیدا کرده است. این منحنی، مشخصه یک دیود پیوندی را نشان میدهد. پدیدههای فیزیکی که مشخصهای به صورت فوق را ایجاد میکنند کاملا با پدیدههای فیزیکی مقاومتهای ساده و خطی متفاوت هستند. تعبیرهای دیگری نظیر «مقاومتهای استاتیکی» (Static Resistance) یا «مقاومتهای دینامیکی» (Dynamic Resistance) نیز از روی مشخصه مقاومتها قابل برداشت است.
موضوع دیگری که در خصوص مقاومتهای غیرخطی وجود دارند این است که مقدار مقاومت در بسیاری از نقاط روی مشخصه، پایدار نیست. به عبارتی، اگر هنگام استفاده از یک مقاومت غیرخطی سعی کنیم که مقدار مقاومت را بر روی یک نقطه خاص نگهداریم، با تغییرات محیطی و بدون تغییر از طرف ما، این مقدار تغییر میکند.
مقاومتها میتوانند متغیر یا نامتغیر با زمان باشند. در واقع در مقاومت متغیر با زمان، مقدار مقاومت با گذشت زمان تغییر کرده و در مقاومت نامتغیر با زمان، مشخصه مقاومت به زمان وابسته نیست. مرسومترین مقاومتی که مورد استفاده قرار میگیرد مقاومت تغییرناپذیر با زمان است. بنابراین با ترکیب خاصیت خطی بودن و خاصیت تغییرپذیری با زمان، میتوانیم چهار نوع مقاومت مختلف را به کار بگیریم.

در مدار الکتریکی المان مقاومت با حرف «R» نمایش داده میشود و رابطه میان ولتاژ دو سر آن و جریان گذرنده از آن به صورت زیر است.
یکای SI مقاومت، ولت بر آمپر است و به علت کاربرد زیادی که این نسبت دارد، با نام اهم (با نماد Ω) شناخته میشود. در واقع میتوان گفت:
از دیدگاه فیزیکی، رسانایی را که وجود آن در یک مدار، مقاومت مشخصی ایجاد میکند مقاومت مینامند. در مدارهای الکتریکی، مقاومت خطی و تغییرناپذیر با زمان، با نماد زیر نمایش داده میشود.

منابع مستقل (نابسته) در مدار الکتریکی چیست ؟
منابع نابسته (Independent Sources)، منابعی هستند که مقدار کمیتی که توسط آنها تولید میشود، به هیچ بخش دیگری از مدار وابسته نباشد. به طور معمول، در مدارهای الکتریکی با دو نوع منبع مستقل از جمله «منبع ولتاژ نابسته» (Independent Voltage Source) و «منبع جریان نابسته» (Independent Current Source) سرو کار داریم.

منبع ولتاژ نابسته المانی است که صرف نظر از اینکه چه جریانی از آن عبور میکند، ولتاژ ثابتی را به مدار ارائه میدهد یا در دو سر خود حفظ میکند. البته این قضیه تا زمانی برقرار است که قوانین KVL و KCL در مدار الکتریکی مورد نظر نقض نشوند. به عنوان مثال، اگر دو سر یک منبع ولتاژ را به یکدیگر متصل کنیم، المان مورد نظر قطعا آسیب میبیند. باتریها و منابع تغذیه موجود، نمونههایی از این منابع ولتاژ نابسته هستند. یک منبع ولتاژ نابسته در مدار با نماد زیر نشان داده میشود.
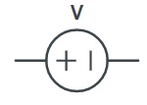
خاصیت مستقل بودن منبع نابسته به این شکل خودش را نشان میدهد که فرض کنید یک منبع ولتاژ نابسته با مقدار ۱۰۰ ولت در مرحله اول به یک مقاومت ۱۰ اهم متصل شده باشد.
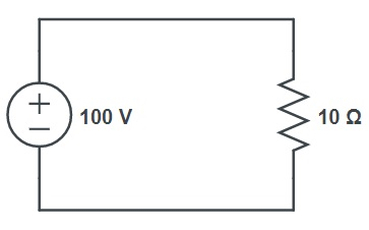
در این شرایط جریانی که از مقاومت ۱۰ اهم عبور میکند عبارت است از:
همانطور که مشاهده میکنید، در این حالت جریان ۱۰ آمپری در مدار برقرار میشود که این جریان از منبع ولتاژ مستقل نیز عبور میکند. در مرحله دوم فرض کنید که مقاومتی با مقدار ۵۰ اهم در مدار حضور دارد.
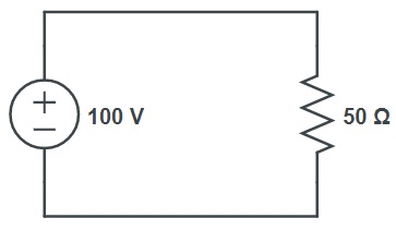
در این شرایط جریانی که از مقاومت ۵۰ اهم عبور میکند عبارت است از:
همانطور که مشاهده میکنید در این مرحله جریانی با مقدار ۲ آمپر از منبع ولتاژ عبور میکند. اما در هر دو شرایط منبع ولتاژ مقدار ولتاژ ۱۰۰ ولت را در دو سر خود قرار داده است. در واقع چون این منبع یک المان مستقل است، تفاوتی نمیکند که جریان ۱۰ آمپری یا جریان ۲ آمپری از آن عبور کند و در هر صورت ولتاژ ۱۰۰ ولتی در دو سر آن قرار دارد. شکل زیر مشخصه یک منبع ولتاژ نابسته با مقدار ۲۰ ولت را نشان میدهد.
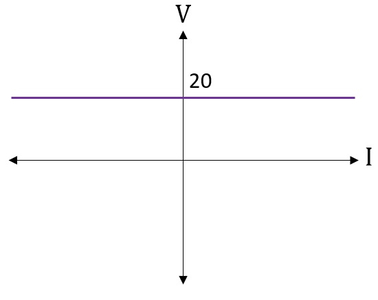
منبع جریان نابسته المانی است که صرف نظر از اینکه چه ولتاژی در دو سر آن برقرار شود، جریان ثابتی را به مدار تزریق میکند. البته این قضیه نیز تا زمانی برقرار است که قوانین KVL و KCL در مدار الکتریکی مورد نظر نقض نشوند. ساختار داخلی منابع ولتاژ نابسته و منابع جریان نابسته با یکدیگر تفاوت دارند و میتوان گفت که منبع جریان مستقل صرفا یک المان است. یک منبع جریان نابسته در مدار الکتریکی به شکل زیر نمایش داده میشود.
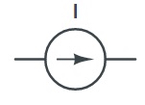
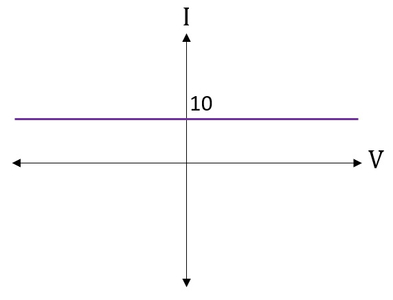
منابع ولتاژ نابسته نظیر باتریها در عمل به سادگی یافت میشوند؛ اما یک منبع جریان نابسته از عناصر داخلی نسبتا پیچیدهتری تشکیل شده است و در نهایت همین تولید جریان ثابت نتیجه وجود یک ولتاژ در مدار است. شکل زیر مشخصه یک منبع جریان نابسته با مقدار ۱۰ آمپر را نشان میدهد.
خازن در مدار الکتریکی چیست ؟
از دیدگاه ریاضی، «خازن» (Capacitor) المانی است که بتوان ولتاژ موجود در دو سر آن و بار الکتریکی ذخیره شده برروی صفحات آنرا در هر لحظه از زمان با یک منحنی نشان داد. این منحنی مشخصه خازن نام دارد. از یک دیدگاه خازنها میتوانند خطی یا غیرخطی باشند. خازنی خطی است که مشخصه آن خط مستقیمی در صفحه v-q باشد که از مبدا مختصات میگذرد. به همین ترتیب خازنی غیرخطی است که خطی نباشد. یعنی یا خط مستقیمی نباشد، یا ممکن است مشخصه آن خط مستقیمی باشد اما این مشخصه از مبدا مختصات عبور نکند. همچنین خازنی را که مشخصه آن با زمان تغییر نکند خازن تغییرناپذیر با زمان، و اگر مشخصه آن با زمان تغییر کند خازن تغییرپذیر با زمان گویند. یک خازن در مدار با نماد زیر نشان داده میشود.
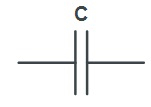
در مدار الکتریکی المان خازن با حرف «C» نمایش داده میشود و رابطه میان ولتاژ دو سر آن و جریان گذرنده از آن به صورت زیر است.
همچنین اگر بخواهیم ولتاژ دو سر خازن را بر حسب جریان گذرنده از آن بنویسیم خواهیم داشت:
در فرمول بالا، ، ولتاژ اولیه خازن است. از یک دیدگاه دیگر، خازن المانی است که از دو صفحه موازی و رسانا تشکیل شده است که این صفحات میتوانند دارای ولتاژ شوند و بین این صفحات نیز عایق وجود دارد. در شکل زیر ساختار یک خازن را مشاهده میکنید.

سلف در مدار الکتریکی چیست ؟
«سلفها» (Inductors) به علت این که در «میدان مغناطیسی» (Magnetic Field) خود، انرژی ذخیره میکنند در مدارهای الکتریکی به کار میروند. عنصری که سلف نامیده میشود ایدهآل شده یک سلف فیزیکی است. به عبارت دقیقتر، یک عنصر دو سر را سلف خواهیم گفت اگر در هر لحظه t از زمان، شار و جریان گذرنده از آن در رابطهای که توسط یک منحنی در صفحه φ-i تعریف میشود صدق میکند. این منحنی، مشخصه سلف نام دارد.
شکل زیر مشخصه یک سلف خطی را نشان میدهد. سلفها نیز مانند مقاومتها و خازنها بسته به اینکه خطی، غیرخطی، تغییرپذیر با زمان یا تغییرناپذیر با زمان باشند به چهار نوع تقسیم میشوند. سلفی را تغییرناپذیر با زمان میگویند که مشخصه آن با زمان تغییر نکند. همچنین، سلفی خطی محسوب میشود که در هر لحظه از زمان، مشخصه آن خط مستقیمی باشد که از مبدا صفحه φ-i بگذرد. یک سلف در مدار با نماد زیر نشان داده میشود.
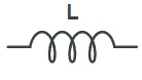
در مدار الکتریکی المان سلف با حرف «L» نمایش داده میشود و رابطه میان ولتاژ دو سر آن و جریان گذرنده از آن به صورت زیر است.
همچنین اگر بخواهیم جریان گذرنده از سلف را بر حسب ولتاژ دو سر آن بنویسیم خواهیم داشت:
که در آن جریان اولیه سلف است.
اما از یک دیدگاه دیگر، سلف المانی است که از یک سیمپیچ و یک هسته تشکیل شده است که این سیمپیچ به دور هسته پیچیده میشود. با عبور جریان از این سیم، میدانی مغناطیس ایجاد میشود که سلف در این میدان، انرژی را ذخیره میکند.

منابع کنترل شده (وابسته) در مدار الکتریکی چیست ؟
در مقابل منابع مستقل، منابع دیگری در مدارهای الکتریکی وجود دارند که مقدار ولتاژ یا جریان آنها به بخشهای دیگری از مدار وابسته است. به این المانها منابع کنترلشده یا وابسته گفته میشود. هنگام تحلیل مدارهای الکتریکی و در هنگام استفاده از قوانین KCL و KVL، این منابع با منابع نابسته هیچ تفاوتی ندارند. اما مقادیر آنها توسط بخش دیگری از مدار کنترل میشود.
در بیشتر مواقع این وابستگی به صورت یک تابع خطی است که در آن و میتوانند ولتاژ یا جریان دو شاخه متفاوت در مدار بوده و k یک ثابت تناسب است. با توجه به این متغیرها چهار نوع منبع وابسته وجود دارد که عبارتند از:
- منبع ولتاژ کنترل شده با ولتاژ
- منبع ولتاژ کنترل شده با جریان
- منبع جریان کنترل شده با ولتاژ
- منبع جریان کنترل شده با جریان
منبع ولتاژ کنترل شده با ولتاژ
«منبع ولتاژ کنترل شده با ولتاژ» (Voltage Controlled Voltage Source) در نگاه اول منبع ولتاژ است اما مقدار آن به طور مستقیم بر حسب ولت بیان نمیشود. بلکه مقدار آن وابسته به ولتاژ یک المان، در بخش دیگری از مدار است. به همین علت، هنگام تعریف به صورت یک المان چهارسر معرفی میشود. در واقع خود این منبع ولتاژ، یک المان دوپایه است اما به ولتاژ المانی وابسته است که خود آن المان نیز دو پایه مجزا دارد. به طورکلی نحوه نمایش این المان در مدار الکتریکی به شکل زیر است.
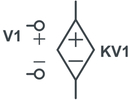
منبع ولتاژ کنترل شده با جریان
«منبع ولتاژ کنترل شده با جریان» (Current Controlled Voltage Source) یک منبع ولتاژ است که مقدار ولتاژی که به مدار ارائه میکند به جریان شاخه دیگری از مدار وابسته است. این المان نیز همانند منبع ولتاژ کنترل شده با ولتاژ، یک المان چهار پایه است که در مدارهای الکتریکی به شکل زیر نمایش داده میشود.
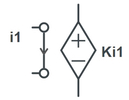
منبع جریان کنترل شده با ولتاژ
«منبع جریان کنترل شده با ولتاژ» (Voltage Controlled Current Source) یک منبع جریان است که مقدار جریانی که به مدار تزریق میکند به ولتاژ شاخه دیگری از مدار وابسته است. این المان نیز یک المان چهار پایه است که در مدارهای الکتریکی به شکل زیر نمایش داده میشود.
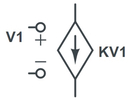
منبع جریان کنترل شده با جریان
«منبع جریان کنترل شده با جریان» (Current Controlled Current Source) یک منبع جریان است که مقدار جریانی که به مدار تزریق میکند به جریان شاخه دیگری از مدار وابسته است. این المان نیز یک المان چهار پایه است که در مدارهای الکتریکی به شکل زیر نمایش داده میشود.
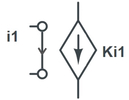
مدارهای مقاومتی چه هستند؟
مدارهای مقاومتی سادهترین مدارهایی هستند که با آنها روبهرو هستیم. این مدارها فاقد عناصر پویا نظیر سلف و خازن هستند و تنها در ساختار آنها عناصری نظیر منابع ولتاژ و جریان (نابسته و وابسته)، کلید و مقاومت وجود دارد. حل مدارهای مقاومتی منجر به ایجاد معادلات جبری میشود. در واقع، زمانی که معادلات KCL و KVL در خصوص این نوع مدارات نوشته میشوند، در انتها تعدادی معادله جبری به وجود میآید که با روشهایی مانند روش کرامر، میتوان تحلیل مدار را تکمیل نمود. به همین علت بحث آنالیز یک مدار الکتریکی را با این نوع مدارات شروع میکنیم تا با ابزار کار آشنا شویم. در بخشهای بعد انواع دیگر مدارهای الکتریکی مانند مدارهای مرتبه اول و مرتبه دوم را نیز بررسی خواهیم کرد. شکل زیر نمونهای از یک مدار بسیار ساده مقاومتی در عمل را نشان میدهد.
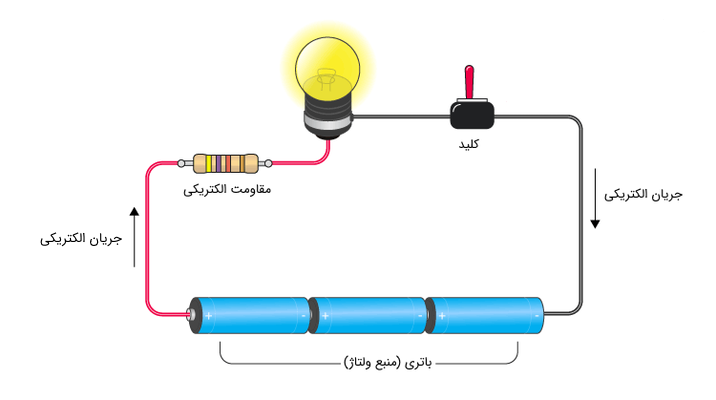
حال مدار الکتریکی فوق را با استفاده از نمادهای مداری مربوط به هر یک از عناصر، رسم میکنیم. در واقع با انجام اینکار مدار را از محیط واقعی به روی کاغذ منتقل میکنیم تا در حالت تئوری آن را تحلیل کنیم. در این حالت مداری به شکل زیر خواهیم داشت.
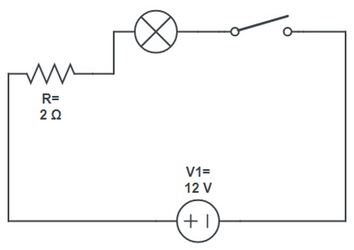
همانطور که مشاهده میکنید، مدار فوق یک مدار تکحلقه است. به منظور محاسبه جریان الکتریکی در این مدار ابتدا معادله KVL را مینویسیم و برای اینکار در جهت عقربههای ساعت در مدار حرکت میکنیم. بنابراین جهت جریان به صورت شکل زیر خواهد بود.
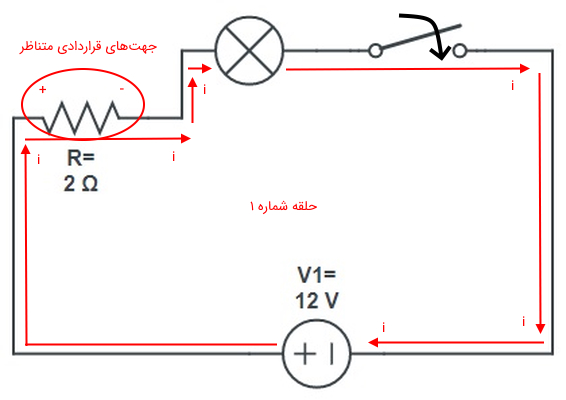
در این مدار فرض میکنیم که لامپ و کلید هیچگونه مقاومت داخلی ندارند. حال با نوشتن معادله KVL در حلقه شماره ۱ خواهیم داشت:
بنابراین:
اتصال سری و موازی مقاومت ها در مدار الکتریکی چیست ؟
مقاومتهای الکتریکی عموما به دو شکل «سری« (Series) و «موازی» (Parallel) به یکدیگر متصل میشوند و اکثر اتصالات پیچیدهتر را میتوان ترکیبی از این دو نوع اتصال دانست. به منظور معادلسازی مقاومتهای موجود در مدار با یک مقاومت معادل، لازم است تا با آرایش آنها آشنا شویم.
اتصال سری در مدار الکتریکی چیست ؟
زمانی که دو یا چند مقاومت به صورت سری به یکدیگر متصل میشوند، جریان یکسانی از آنها عبور میکند. در این نوع اتصال، پایه انتهایی هر مقاومت به پایه ابتدایی مقاومت بعدی متصل میشود. در این حالت ولتاژ بین مقاومتهای سری تقسیم میشود و با توجه به اینکه از همه آنها جریان یکسانی عبور میکند، ایجاد آسیب و قطعی در هر یک از مقاومتها سبب میشود که هیچ جریانی از هیچ یک از مقاومتها عبور نکند. شکل زیر آرایش دو مقاومت به صورت سری را نشان میدهد.
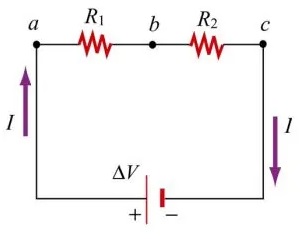
با قراردادن یک مقاومت معادل بهجای دو مقاومت موجود، مداری به شکل زیر خواهیم داشت.

مقدار این مقاومت معادل برابر است با:
از آنجایی که جریان یکسانی از دو مقاومت سری عبور میکند، پس هنگام قرار دادن یک مقاومت معادل همان جریان نیز از این مقاومت عبور میکند. اما ولتاژی که در دو سر مقاومت معادل قرار میگیرد برابر است با جمع ولتاژهای موجود در دو سر مقاومتهای معادل. بنابراین:
بنابراین اگر در بخشی از یک مدار، از N مقاومت سری استفاده شده باشد، میتوان آنها را با مقاومتی معادل برابر با مقدار زیر جایگزین کرد.
با توجه به رابطه بالا واضح است که اگر مقدار یکی از مقاومتها از بقیه بسیار بزرگتر باشد، میتوان از بقیه مقاومتها صرف نظر کرد و مقاومت معادل را برابر با مقاومت بزرگتر در نظر گرفت. جریان و ولتاژ این مقاومت معادل نیز به ترتیب برابر است با:
اتصال موازی در مدار الکتریکی چیست ؟
زمانی که دو یا چند مقاومت به صورت موازی به یکدیگر متصل میشوند، ولتاژ یکسانی در دو سر آنها قرار میگیرد. در این نوع اتصال، پایههای ابتدایی همه مقاومتها به یکدیگر متصل میشده و پایههای انتهایی نیز به یکدیگر متصل میشوند. در این حالت جریان بین مقاومتهای موازی تقسیم میشود و بسته به مقدار مقاومت، نسبت مشخصی از جریان کل از آن عبور میکند. در این حالت خارج شدن هر یک از مقاومتها از مدار به طورکلی آسیبی به عملکرد مدار نمیرساند و بقیه مقاومتهای موجود میتوانند به کار خود ادامه دهند. البته اگر شرایط خاصی وجود داشته باشد و خروج یک مقاومت باعث ایجاد جریان شدیدی در باقی مقاومتها شود، به سادگی نمیتوان آن مقاومت را از مدار خارج کرد. شکل زیر آرایش دو مقاومت به صورت موازی را نشان میدهد.
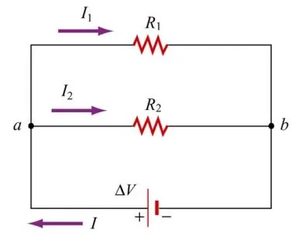
با قراردادن یک مقاومت معادل بهجای دو مقاومت موجود، مداری به شکل زیر خواهیم داشت.
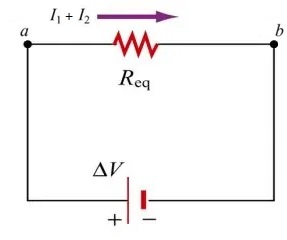
مقدار این مقاومت معادل برابر است با:
از آنجایی که در دو سر مقاومتهای موازی ولتاژ یکسانی قرار میگیرد، پس هنگام قرار دادن یک مقاومت معادل همان ولتاژ نیز در دو سر این مقاومت قرار میگیرد. اما جریانی که از مقاومت معادل عبور میکند برابر با جمع جریانهای مقاومتهای موازی است. بنابراین:
به این ترتیب، اگر در بخشی از یک مدار، از N مقاومت موازی استفاده شده باشد، میتوان آنها را با مقاومتی معادل برابر با مقدار زیر جایگزین کرد:
ولتاژ و جریان این مقاومت معادل نیز به ترتیب برابر است با:
روش های آنالیز مدارهای مقاومتی کدام هستند؟
در بحث آنالیز مدارهای الکتریکی، در گام اول مدارهای مقاومتی را مورد بررسی قرار میدهیم؛ زیرا این مدارات ساختار سادهتری نسبت به سایر مدارهای الکتریکی دارند. اما به طور کلی، آنالیز تمامی مدارهای الکتریکی فشرده بر اساس قوانین ولتاژ و جریان کیرشهف انجام میشود.
آنالیز مدار به روش گره چگونه انجام می شود؟
تحلیل مدار الکتریکی به روش گره، به طور مستقیم بر اساس قانون KCL و جهتهای قراردادی متناظر پایهریزی شده است. در این روش، معادلات مربوط به یک مدار، بر اساس ولتاژ گرههای آن مدار نوشته میشود. اما در نهایت جریان شاخهها محاسبه میشوند. به عنوان مثال قصد داریم مدار زیر را به روش گره تحلیل کنیم. بدین معنی که ولتاژ گرهها و جریان شاخهها را محاسبه کنیم.
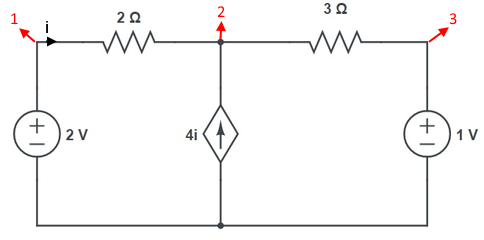
در روش تحلیل گره، ابتدا گرههای موجود را شمارهگذاری میکنیم. سپس در گرههایی که نیاز است معادلات KCL را مینویسیم. همچنین این نکته را در نظر میگیریم که اگر گره، به شکل مستقیم به منبع ولتاژ مستقل متصل بود، ولتاژ گره را برابر با منبع ولتاژ در نظر میگیریم. حال با شمارهگذاری گرهها و نامگذاری آنها خواهیم داشت:
از آنجایی که گرههای 1 و 3 مستقیما به منبع ولتاژ متصل هستند میتوانیم بگوییم:
همچنین در شاخهای که جریان در آن برقرار است، میتوانیم قانون اهم را به شکل زیر بنویسیم:
با قراردادن معادله فوق به جای در معادله KCL2 آن را به شکل زیر بازنویسی میکنیم:
با قرار دادن مقادیر ولتاژ گرههای 1 و 3 خواهیم داشت:
آنالیز مدار به روش مش چگونه انجام می شود؟
در تحلیل مدار به روش مش، به طور مستقیم از قانون KVL استفاده میشود. به این شکل که هنگام تحلیل یک مدار به روش مش، معادلات مدار مربوطه بر اساس جریان شاخهها نوشته میشود. اما در نهایت مقادیر ولتاژ گرهها محاسبه میشوند.

در تحلیل مدار الکتریکی به روش مش، لازم است در ابتدا با مفهوم مش و حلقه آشنا شویم. به طور کلی، مش مسیر بستهای است که مجموع پتانسیلها در آن صفر باشد. اما به مسیر بستهای که از دو یا چند مش تشکیل میشود، حلقه گفته میشود. در تحلیل مدار به روش مش، ابتدا جریان هر مش را نامگذاری میکنیم و جهت آنرا نیز معین میکنیم (بهتر است که جهت جریان در همه مشها یکسان باشد). سپس، در مشها معادلات KVL را مینویسیم. در مشهای ۱ و ۲ در مدار فوق به دلیل وجود منبع جریان نمیتوانیم معادلات KVL را بنویسیم. به همین علت این معادله را در مش شماره ۳ مینویسیم. بنابراین داریم:
بنابراین داریم:
با بررسی جریانهای ورودی و خروجی در شاخهای که منبع جریان وابسته در آن حضور دارد میتوان گفت:
در نتیجه خواهیم داشت:
نکته مهمی که در نوشتن معادلات KVL در مشها وجود دارد این است که در مشی که منبع جریان وجود دارد، نمیتوانیم معادلات KVL را بنویسیم. به عبارتی اگر هنگام نوشتن معادلات KVL در هر مش به منبع جریان برخورد کردیم، از نوشتن معادله در آن دسته مشها صرف نظر میکنیم. در واقع اگر مشی وجود نداشت که در آن منبع جریان وجود نداشته باشد، از حلقههای بزرگتر استفاده میکنیم.
آنالیز مدار به روش ترکیبی چگونه انجام می شود؟
روشهای تحلیل گره و مش روشهایی هستند که طبق یک الگوریتم ثابت جلو میروند و در نهایت با حل یک سری معادلات، کمیتهای مورد نظر یافت میشوند. اگر مدار مورد نظر، یک مدار مقاومتی باشد، معادلاتی که از نوشتن قوانین KCL و KVL حاصل میشوند، معادلات جبری خواهند بود. اما یکی از معایب این روشها این است که با پیچیدگی مدار و افزایش تعداد گرهها و شاخهها، تعداد معادلات نیز افزایش می یابند. به طوری که اگر تعداد گرهها و مشهای مدار از حدی بالاتر روند، حل معادلات به صورت دستی امکانپذیر نخواهد بود. به همین خاطر از یک روش خلاقانهتر برای تحلیل مدارهای الکتریکی بهره میگیریم.
در این روش، ابتدا با استفاده از قانون KCL جریان شاخههای مدار را مشخص میکنیم و سعی میکنیم کمترین تعداد متغیر را در شاخهها ایجاد کنیم. در گام بعد با استفاده از معادلات KVL ولتاژ دو سر المانهای موجود در مشها را بر حسب جریان شاخهها مینویسیم. در نهایت با حل معادلات به دست آمده مقادیر جریان شاخهها را به دست میآوریم. در مدار شکل زیر، قصد داریم آنالیز را به صورت ترکیبی انجام دهیم.

در گام اول با استفاده از معادلات KCL، جریان شاخهها را به صورت زیر مشخص میکنیم.
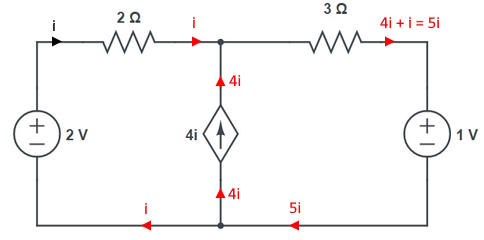
زمانی که جریان شاخههای موجود در مدار مطابق شکل فوق مشخص شدند، در حلقه مشخص شده مطابق شکل زیر معادله KVL را مینویسیم.
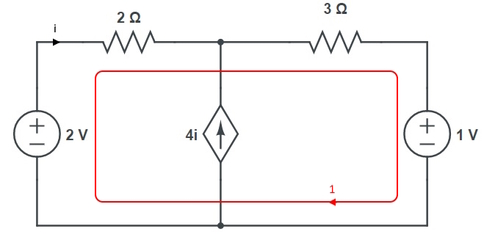
بنابراین:
با حل معادله فوق، جریان i برابر است با:
مدارهای مرتبه اول چه هستند؟
تا به اینجا به مدارهای مقاومتی آشنا شدیم و گفتیم که تحلیل این نوع مدارها، منجر به تشکیل معادلات جبری میشود. اگر بخواهیم از همین زاویه مدارهای مرتبه اول را معرفی کنیم میتوانیم بگوییم که حل این نوع مدارها، منجر به تشکیل معادلات دیفرانسیل مرتبه اول میشود. در واقع به همین علت است که این مدارها، مرتبه اول نامیده میشوند.
در مدارهای مرتبه اول یک عنصر ذخیرهکننده انرژی یا پویا مانند سلف یا خازن به صورت مستقل وجود دارد. کلمه «اول» در نام این نوع مدارات، میتواند به وجود یک عنصر پویا اشارهای داشته باشد. سادهترین مدارهای مرتبه اول، مدارهای RL و RC هستند که در ادامه به طور مختصر آنها را بررسی خواهیم کرد.
مدارهای RC چه هستند ؟
این نوع مدارها، از یک مقاومت و یک خازن به صورت زیر تشکیل شدهاند.
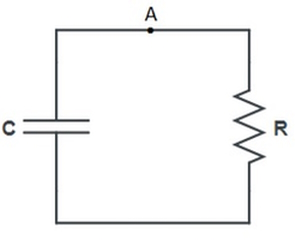
با نوشتن معادله KCL در گره A خواهیم داشت:
که بر حسب ولتاژ میتوان نوشت:
اگر ولتاژ دو سر مقاومت را به صورت و ولتاژ دو سر خازن را به صورت در نظر بگیریم. با توجه به اینکه مقاومت و خازن با یکدیگر موازی هستند بنابراین داریم:
بنابراین میتوان معادله KCL را به شکل زیر نوشت:
اگر طرفین معادله به دست آمده را بر تقسیم کنیم خواهیم داشت:
معادله به دست آمده یک معادله دیفرانسیل مرتبه اول است. میدانیم که ساختار جواب چنین معادلهای در حالت کلی به صورت زیر است:
برای یافتن مقدار باید از شرایط اولیه مدار استفاده کنیم. اگر فرض کنیم که در زمان ولتاژ خازن دارای مقدار اولیه باشد در این صورت:
از طرفی با توجه به اینکه خازن و مقاومت با یکدیگر موازی هستند و ولتاژ یکسانی دارند، میتوان گفت:
برای محاسبه جریان خازن، ابتدا رابطه ولتاژ دو سر خازن و جریان گذرنده از آنرا به صورت زیر در نظر میگیریم:
یعنی:
در نهایت داریم:
در مدارهای RC، ثابت زمانی به صورت و بر حسب ثانیه مطرح میشود.
مدارهای RL چه هستند ؟
مدارهای RL از یک مقاومت و یک سلف تشکیل شدهاند. شکل زیر یک مدار RL را نشان میدهد.

با نوشتن معادله KCL در گره A خواهیم داشت:
با نوشتن معادله KVL در این مدار تکحلقه خواهیم داشت:
حال با توجه به اینکه جهت جریان مقاومت و سلف، عکس یکدیگر هستند میتوان گفت:
اگر طرفین معادله را بر تقسیم کنیم خواهیم داشت:
با حل معادله دیفرانسیل به دست آمده جریان سلف به صورت زیر به دست خواهد آمد.
در مدارهای RL، ثابت زمانی به صورت و بر حسب ثانیه مطرح میشود.
یکی از موضوعات مهمی که در خصوص مدارهای مرتبه اول وجود دارد این است که در این مدارها، تنها یک عنصر پویا به صورت مستقل وجود دارد. به عنوان مثال ممکن است در یک مدار الکتریکی، ممکن است یک مقاومت و دو خازن وجود داشته باشد اما این خازنها به صورت سری و موازی با یکدیگر ساده شوند. جنین مداری را نمیتوان یک مدار الکتریکی مرتبه دوم در نظر گرفت؛ زیرا دو خازن موجود در مدار، مستقل از یکدیگر نیستند و با سادهسازی به یک خازن تبدیل میشوند.
مدارهای مرتبه دوم چه هستند؟
در مدارهای مرتبه دوم، دو عنصر ذخیرهکننده انرژی یا پویا به صورت مستقل وجود دارد. تحلیل ان نوع مدارها در نهایت منجر به تشکیل یک معادله دیفرانسیل مرتبه دوم میشود که با حل آن معادله دیفرانسیل، تحلیل مدار کامل میگردد. شکل زیر نمونهای از یک مدار مرتبه دوم را نشان میدهد.
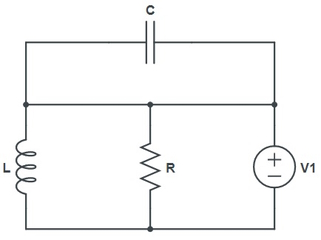
تحلیل یک مدار الکتریکی مرتبه دوم به خلاقیت بیشتری نسبت به مدارهای مقاومتی و مرتبه اول، نیاز دارد. اصلیترین گام در تحلیل این نوع مدارات تا زمانی است که معادله دیفرانسیل مرتبه دوم، تشکیل میشود. در واقع همان بخش تشکیل معادله دیفرانسیل است که روش تحلیل این دسته از مدارها را از بقیه متمایز میکند.
سوالات مرتبط با مدارهای الکتریکی و انواع آنها
در این بخش، به برخی از پرتکرارترین سوالات مرتبط با مبحث مدار الکتریکی به طور مختصر پاسخ میدهیم.
جریان الکتریکی چگونه در یک مدار الکتریکی برقرار می شود؟
با ایجاد اختلاف پتانسیل در دو سر مدار، بارهای الکتریکی شروع به حرکت میکنند و جریان الکتریکی در مدار برقرار میگردد.
تفاوت نیرو محرکه الکتریکی با اختلاف پتانسیل و ولتاژ چیست؟
نیرو محرکه الکتریکی عاملی است که سبب به وجود آمدن اختلاف پتانسیل میشود. در حقیقت اختلاف پتانسیل به دلیل وجود نیرو محرکه الکتریکی به وجود میآید. از طرفی در دو سر عنصری که اختلاف پتانسیل را به وجود آورده است، ولتاژ ایجاد میشود.
قوانین بنیادی مدارهای الکتریکی چه نام دارند؟
دو قانون اساسی در مدارهای الکتریکی وجود دارد که به قوانین کیرشهف معروف هستند. این قوانین، قانون جریان کیرشهف یا KCL و قانون ولتاژ کیرشهف یا KVL هستند.
منبع ولتاژ مستقل در مدار الکتریکی چیست و چه تفاوتی با منبع ولتاژ وابسته دارد؟
منبع ولتاژ مستقل صرف نظر از اینکه چه جریانی از آن عبور میکند ولتاژ ثابتی را به مدار ارائه میکند. تفاوت منبع ولتاژ مستقل و وابسته در این است که ولتاژ یک منبع ولتاژ مستقل به هیچ کمیت دیگری وابسته نیست. در حالی که ولتاژ یک منبع ولتاژ وابسته به ولتاژ یا جریان یک عنصر یا بخش دیگری از مدار الکتریکی وابسته است.
قوانین تقسیم ولتاژ و تقسیم جریان در مدارهای الکتریکی چیست؟
این قوانین بسته به اینکه المان مورد نظر جه ماهیتی دارد مشخص میکند که ولتاژ یا جریان با چه نسبتهایی بین آنها تقسیم میشود.
مدارهای مقاومتی و مدارهای مرتبه اول از نظر ساختار چه تفاوتی با یکدیگر دارند؟
در مدارهای مقاومتی عناصر ذخیرهکننده انرژی مانند سلف یا خازن وجود ندارند. در حالی که در مدارهای مرتبه اول، یک عنصر پویا به شکل مستقل حضور دارد.
روش تحلیل مدارهای مقاومتی و مدارهای مرتبه اول چه تفاوتی با یکدیگر دارند؟
تحلیل یک مدار الکتریکی مقاومتی منجر به تشکیل معادلات جبری میشود. در حالی که با تحلیل یک مدار مرتبه اول، یک معادله دیفرانسیل مرتبه اول به دست میآید که با حل آن، کمیتهای مدار مورد نظر به دست میآیند.
آزمون مدار الکتریکی
۱. بار الکتریکی چیست و فرق ماده خنثی با ماده بدون بار کدام است؟
بار الکتریکی فقط در فلزات دیده میشود و ماده خنثی هیچ باری ندارد.
بار الکتریکی تنها در باتری وجود دارد و ماده خنثی همیشه فاقد بار است.
بار الکتریکی همان جریان الکتریکی است و ماده بدون بار نمیتواند الکترون داشته باشد.
بار الکتریکی خاصیتی است که همه مواد دارند و ماده خنثی مجموع بار مثبت و منفی برابر دارد.
بار الکتریکی ویژگی بنیادی ماده است و هیچ ذرهای از این ویژگی خالی نیست. ماده خنثی به مادهای گفته میشود که تعداد بار مثبت و منفی آن با هم برابر هستند، نه اینکه اصلا بار نداشته باشد. در واقع برخلاف ماده بدون بار فرضی، ماده خنثی همچنان بارهای مثبت و منفی دارد اما آنها همدیگر را خنثی میکنند.
۲. در مدار الکتریکی، عملکرد نیرو محرکه (EMF) چیست و چه تفاوتی با نیروی فیزیکی دارد؟
نیرو محرکه موجب افزایش مقاومت مدار میشود و واحدش آمپر است.
نیرو محرکه مدار را تنها در حضور میدان مغناطیسی فعال میکند و واحدش نیوتن است.
نیرو محرکه بدون تاثیر بر جریان، صرفا ولتاژ مدار را بارها تغییر میدهد و واحدش فاراد است.
نیرو محرکه جریان الکتریکی را در مدار با ایجاد اختلاف پتانسیل برقرار میکند و واحد آن ولت است.
EMF عامل ایجاد جریان در مدار است و باتری یا سلول خورشیدی آن را ایجاد میکند؛ اندازهگیری آن با ولت انجام میشود، نه نیوتن یا دیگر واحدها.
۳. در مدار الکتریکی، اگر جهت قراردادی جریان را به سمت مخالف انتخاب کنیم، نتیجه کدام خواهد بود؟
مقادیر ریاضی جریان و ولتاژ معکوس علامت میشوند اما تحلیل نهایی همان است.
نقش عناصر فعال و غیر فعال در مدار عوض میشود.
معادلات مدار دیگر معتبر نخواهند بود و باید دوباره نوشته شوند.
مقادیر توان مصرفی اجزاء به طور اساسی تغییر میکند.
اگر جهت قراردادی جریان در یک مدار تغییر کند، تنها علامت مقادیر ریاضیای مانند جریان و در نتیجه ولتاژها نسبت به جهت جدید عوض میشود، اما اصول و نتیجه کلی تحلیل تغییر نمیکنند. یعنی با پایبندی به یک جهت انتخابشده، تمامی معادلات درست و کامل باقی میمانند.
۴. کدام ویژگی عنصر مقاومت نشاندهنده خطی یا غیرخطی بودن آن است و چرا در انتخاب آن برای مدار اهمیت دارد؟
اثر فرکانس بر رفتار مقاومت در مدار
وجود رابطه مستقیم و ساده میان ولتاژ و جریان
توانایی تحمل ولتاژ بالا در شرایط خاص
ثابت بودن مقدار فیزیکی مقاومت در زمان
داشتن رابطه مستقیم میان ولتاژ و جریان یا همان مشخصه v-i، تعیینکننده خطی یا غیرخطی بودن مقاومت است. اگر این رابطه خطی باشد (مثل مقاومت کلاسیک)، تحلیل و پیشبینی رفتار مدار سادهتر خواهد بود و مقاومت انتخابشده عملکرد مطلوبی در شرایط استاندارد ارائه میدهد. سایر گزینهها، مانند ثابت بودن مقدار فیزیکی، توانایی تحمل ولتاژ بالا یا اثرپذیری از فرکانس، بر موضوع خطی یا غیرخطی بودن مقاومت تاثیری ندارند بلکه هرکدام بیانگر ویژگی متفاوت یا تاثیر متفاوت در عملکرد مدار هستند.
۵. در چه شرایطی قوانین کیرشهف برای تحلیل مدارهای فشرده معتبر نیستند و دلیل این موضوع چیست؟
زمانی که مدار فقط از مقاومت و خازن تشکیل شده باشد، قوانین کیرشهف صدق نمیکند.
در فرکانسهای بالا که طول موج سیگنال با ابعاد مدار قابل مقایسه باشد اثرات الکترومغناطیسی مهم میشوند.
اگر همه عناصر مدار خطی باشند، قوانین کیرشهف همواره برقرار است.
قوانین کیرشهف فقط در مدارهایی بیمنبع تغذیه معتبر هستند و با اضافه شدن منبع نقض میشوند.
وقتی طول موج سیگنال در فرکانسهای بالا با ابعاد فیزیکی مدار قابل مقایسه شود، اثرات الکترومغناطیسی چشمگیر شده و مدار دیگر «فشرده» محسوب نمیشود. در این حالت، تحلیل مدار با قوانین کیرشهف امکانپذیر نیست چون جریانها و ولتاژها ممکن است در بخشهای مختلف مدار کاملا ناهمگن باشند. در سایر حالتها مانند وجود عناصر خطی یا ترکیب مقاومت و خازن، یا نوع منبع، قوانین کیرشهف نقض نمیشوند و همچنان معتبر باقی میمانند.
۶. برای محاسبه جریان کل یک مدار مقاومتی ساده با استفاده از قانون KVL چه کاری باید انجام داد؟
در نظر گرفتن جهت قراردادی جریان و ولتاژ در همه شاخهها
جمع جبری جریانها در تمام شاخهها
تقسیم کل مقاومت بر مجموع ولتاژ منابع
جمع جبری ولتاژ منابع و تقسیم بر مجموع مقاومتها
با استفاده از قانون KVL، باید مجموع جبری ولتاژ منابع را بدست آورد و آن را بر مجموع مقاومتهای موجود در مسیر مدار تقسیم کرد تا مقدار جریان کل به دست آید.
۷. در فرآیند ایجاد جریان الکتریکی در مدار، نقش هر یک از ولتاژ، اختلاف پتانسیل و نیرو محرکه (EMF) چیست؟
اختلاف پتانسیل باعث تولید نیرو محرکه و سپس ولتاژ را در مدار تعیین میکند.
نیرو محرکه ابتدا اختلاف پتانسیل را ایجاد میکند و سپس ولتاژ جریان خروجی بین دو نقطه ظاهر میشود.
ولتاژ مستقیما عامل تولید نیرو محرکه و اختلاف پتانسیل است.
نیرو محرکه و ولتاژ همزمان و مستقل باعث حرکت بار در مدار میشوند.
در زنجیره ایجاد جریان، ابتدا نیرو محرکه (EMF) نقش شروعکننده را دارد و اختلاف پتانسیل میان دو نقطه ایجاد میکند. این اختلاف پتانسیل زمینه حرکت بارها و در نتیجه ظهور ولتاژ بین دو سر المان مدار را فراهم میکند. پس نیرو محرکه آغازگر است، اختلاف پتانسیل مسیر را فراهم میآورد و ولتاژ خروجی قابل اندازهگیری نتیجه نهایی است.
۸. در مدارهایی که مقاومتها بهصورت سری یا موازی بسته میشوند، جریان و ولتاژ در هر آرایش چه تفاوتی با هم دارند؟
در موازی، جریان تقسیم میشود و ولتاژ در همه مقاومتها متفاوت است.
در موازی، جریان و ولتاژ هر دو در همه مقاومتها متفاوتاند.
در سری، هم جریان و هم ولتاژ تقسیم میشوند.
در سری، ولتاژ تقسیم میشود و جریان در همه مقاومتها یکسان است.
در آرایش سری، جریان عبوری از هر مقاومت برابر است و تغییر نمیکند، اما ولتاژ بین مقاومتها تقسیم میشود. علت این رفتار آن است که یک مسیر جریان وجود دارد و همه مقاومتها یک جریان یکسان دریافت میکنند، ولی افت ولتاژ روی هر مقاومت، جمعشونده است. برخلاف آن، در اتصال موازی، ولتاژ دو سر همه مقاومتها یکسان باقی میماند و جریان است که تقسیم میشود.
۹. خازن از چه ساختاری ساخته میشود و رابطه اصلی جریان و ولتاژ آن چیست؟
سیم پیچ با هسته آهنی و جریان همواره ثابت
دو صفحه رسانا با عایق بینشان و جریان برابر ظرفیت ضرب در مشتق ولتاژ
دو مقاومت موازی و جریان جمع ولتاژهای دو سر آنها
سه صفحه رسانا با ولتاژ همواره یکسان بین صفحات
در خازن، ساختار اصلی شامل دو صفحه رسانا است که یک ماده عایق میان آنها قرار دارد. رابطه کلیدی میان جریان و ولتاژ این عنصر آن است که جریان عبوری از خازن برابر ظرفیت آن (C) ضرب در نرخ تغییر ولتاژ (مشتق ولتاژ نسبت به زمان) است. ساختارهایی مانند سیم پیچ یا چند مقاومت، توصیف خازن نیستند و همچنین در خازن، جریان ثابت و ولتاژ همواره یکسان میان چند صفحه وجود ندارد.
۱۰. کدام دستهبندی زیر، انواع منابع وابسته را در مدار الکتریکی به طور صحیح بیان میکند؟
منبع ولتاژ کنترلشده جریان، منبع جریان کنترلشده ولتاژ، منبع ولتاژ کنترلشده ولتاژ، منبع جریان کنترلشده جریان
منبع جریان مستقل، منبع ولتاژ مستقل، منبع وابسته به دما، منبع وابسته به نور
منبع سلف کنترلشده، منبع خازن وابسته، منبع دیود کنترلشده، منبع ترانزیستور وابسته
منبع مقاومت وابسته به دما، منبع ولتاژ وابسته به فرکانس، منبع جریان وابسته به فشار، منبع ولتاژ وابسته به نور
در مدار الکتریکی منابع وابسته چهار نوع اصلی دارند: «منبع ولتاژ کنترلشده جریان»، «منبع جریان کنترلشده ولتاژ»، «منبع ولتاژ کنترلشده ولتاژ» و «منبع جریان کنترلشده جریان». این منابع ولتاژ یا جریان خود را با توجه به مقدار ولتاژ یا جریان دیگری در مدار تعیین میکنند و نقش کلیدی آنها در امکان پیادهسازی تقویتکنندهها و مدارهای پیچیده است.
۱۱. چه تفاوتی میان مشخصه ولتاژ-جریان مقاومت خطی، غیرخطی و متغیر با زمان وجود دارد؟
در مقاومت متغیر با زمان، مقدار مقاومت در طول زمان تغییر میکند، اما ممکن است v-i خطی بماند.
در مقاومت خطی، نمودار v-i میتواند با ولتاژ زیاد منحنی شود.
در مقاومت غیرخطی، نمودار v-i خمیده و وابسته به مقدار ولتاژ یا جریان است.
رابطه v-i مقاومت خطی یک خط مستقیم همواره از مبداء است.
در مقاومت غیرخطی، رفتار مشخصه v-i به گونهای است که نمودار آن خمیده شده و مقدار مقاومت برای ولتاژها یا جریانهای مختلف متفاوت است. در حالی که مقاومت خطی همیشه یک رابطه مستقیم و از مبداء دارد (نمودار خط مستقیم)، در مقاومت غیرخطی واکنش عنصر مداری نسبت به افزایش ولتاژ یا جریان ثابت نیست و باعث میشود نمودار شکل خمیده داشته باشد. این تفاوت باعث میشود رفتار مدارهایی که عناصر غیرخطی دارند پیچیدهتر تحلیل شود. در مقابل، جمله «در مقاومت خطی، نمودار v-i میتواند با ولتاژ زیاد منحنی شود» نادرست است چون خطی بودن به معنای حفظ رابطه مستقیم صرفنظر از مقدار ولتاژ یا جریان است، و در مقاومت متغیر با زمان اگرچه مقدار مقاومت تغییر میکند، اما شکل کلی نمودار v-i لزوما خمیده نمیشود.
۱۲. کدام جمله به درستی نقش خازن و سلف را در مدیریت انرژی مدار بیان میکند؟
خازن و سلف هر دو فقط ولتاژ را در مدار تثبیت میکنند.
خازن انرژی را به صورت بار الکتریکی ذخیره و سلف انرژی را در میدان مغناطیسی ذخیره میکند.
سلف فقط برای کاهش نویز به کار میرود و خازن نوسان ایجاد میکند.
خازن و سلف فقط در مدارهای فرکانس بالا استفاده میشوند.
ذخیره انرژی توسط خازن از طریق بار الکتریکی روی صفحات و توسط سلف در میدان مغناطیسی اطراف سیمپیچ انجام میشود. این ویژگی اصلی این دو عنصر است که نقش مهمی در مدیریت گذراها و پایداری مدار دارد.
۱۳. اگر ولتاژ لحظهای و جریان عبوری از یک نقطه در مدار مشخص باشند، چطور باید توان لحظهای را بیابید؟
مقدار ولتاژ را از جریان کم کنید تا توان داشته باشید.
ولتاژ لحظهای را با عدد ثابت جمع کنید و سپس در جریان ضرب کنید.
ولتاژ را بر جریان تقسیم کنید تا توان به دست آید.
ضرب ولتاژ لحظهای در جریان عبوری را محاسبه کنید.
برای یافتن توان لحظهای کافیست ولتاژ لحظهای را در جریان همان لحظه ضرب کنید، چون توان برابر با حاصلضرب این دو کمیت است. محاسبههایی چون تقسیم یا کم کردن این دو مقدار توان را نمیدهند و جمع ولتاژ با مقدار ثابت هم صحیح نیست. فقط با عمل ضرب مقدار درست توان به دست میآید.
۱۴. در تحلیل مدارهای مقاومتی، روش گره و روش مش هر یک بر اساس کدام کمیتها استخراج میشوند و تفاوت کلیدی روند حل چگونه است؟
هر دو روش فقط برای مدارهای سری قابل استفادهاند.
هر دو روش گره و مش فقط جریان در شاخهها را بررسی میکنند.
روش گره بر ولتاژ گرهها، روش مش بر جریان حلقهها متمرکز است.
روش گره ولتاژ هر المان را با KVL، روش مش جریانها را با KCL به دست میآورد.
در روش گره، تمرکز اصلی بر ولتاژ گرهها است و معادلات با استفاده از قانون جریان کیرشهف (KCL) تدوین میشوند تا ولتاژ نقاط مختلف تعیین گردد. در مقابل، روش مش بر جریان حلقهها استوار است و با کمک قانون ولتاژ کیرشهف (KVL) جریان حلقهها را محاسبه میکند. به همین دلیل، عبارت «روش گره بر ولتاژ گرهها و روش مش بر جریان حلقهها متمرکز است» تنها توضیح دقیق تفاوت آنها است. گزینههایی که به بررسی فقط جریان شاخهها اشاره دارند یا تنها مدارهای سری را در نظر میگیرند صحیح نیستند، زیرا هر دو روش برای مدارهای پیچیدهتر و انواع مختلف به کار میروند. همچنین، معکوس کردن نقش KCL و KVL برای این روشها نادرست است.
۱۵. در مدار مرتبه اول و دوم، تفاوت اصلی در عناصر ذخیرهکننده انرژی و نوع معادله دیفرانسیل چیست؟
مدار مرتبه اول بدون عنصر ذخیرهکننده انرژی تحلیل میشود، اما مدار مرتبه دوم همیشه یک خازن دارد.
مدار مرتبه اول فقط یک عنصر ذخیرهکننده انرژی دارد، اما مدار مرتبه دوم دو عنصر ذخیرهکننده انرژی دارد و معادله دیفرانسیل آنها نیز متفاوت است.
مدار مرتبه اول و دوم هر دو به معادله جبری نیاز دارند و عناصر ذخیرهکننده انرژی اهمیتی ندارند.
در مدار مرتبه اول و دوم تعداد عناصر ذخیرهکننده انرژی برابر است اما نوع معادله دیفرانسیل فرق میکند.
در مدار مرتبه اول فقط یک عنصر ذخیرهکننده انرژی مانند سلف یا خازن وجود دارد و معادله دیفرانسیل حاصل، مرتبه اول است. در مدار مرتبه دوم دو عنصر ذخیرهکننده انرژی بهصورت مستقل داریم و تحلیل مدار نیازمند معادله دیفرانسیل مرتبه دوم خواهد بود. گزینههای دیگر نادرستاند زیرا تعداد عناصر ذخیرهکننده انرژی در مدار مرتبه اول و دوم یکسان نیست و وجود خازن الزامی برای مدار مرتبه دوم نیست. همچنین تحلیل این مدارها فقط بر پایه معادله جبری انجام نمیگیرد و عناصر ذخیرهکننده انرژی نقشی کلیدی دارند.
۱۶. برای بررسی اثر بارگذاری روی دو منبع ولتاژ مستقل در مدار مقاومتی، کدام روش تحلیل مناسبتر است؟
استفاده از روش مش برای تعیین جریان در هر حلقه
مقایسه ولتاژ دو سر مقاومتها با تغییر مقاومت بار
استفاده از روش گره برای محاسبه ولتاژ هر گره
استفاده تنها از قانون کیرشف جریان (KCL) در گره خروجی
در بررسی رفتار منابع ولتاژ مستقل هنگام تغییر بارگذاری، مقایسه ولتاژ دو سر مقاومتها با تغییر مقدار مقاومت بار روشی مناسب است؛ زیرا این کار نحوه تقسیم ولتاژ و رفتار منابع هنگام تغییر شرایط مدار را نشان میدهد. استفاده از روش گره یا مش روشهای کلی تحلیل مدار هستند اما مقایسه مستقیم ولتاژ بر مقاومتها روند تغییر اثر بارگذاری را شفافتر نشان میدهد. بکارگیری صرف قانون کیرشف جریان (KCL) کافی نیست، چون اطلاعاتی درباره تغییر ولتاژها نمیدهد.
۱۷. در یک گره مرکب مدار، قانون جریان کیرشهف (KCL) چگونه میتواند در تعیین جریانهای مجهول موثر باشد؟
با جمع جبری جریانهای ورودی و خروجی و برابر قرار دادن آنها با صفر معادله مورد نیاز برای حل مجهولات ایجاد میشود.
با استفاده از مقاومت معادل گره، فقط مجموع جریان کل را بدون نیاز به معادله محاسبه میکند.
اختلاف ولتاژ بین دو انتهای گره محاسبه و جریانهای مجهول از آن استخراج میشود.
کلیه جریانهای عبوری از شاخهها به صورت مستقل اندازهگیری و مستقیما تعیین میشوند.
قانون جریان کیرشهف (KCL) میگوید که مجموع جبری جریانهای ورودی و خروجی به یک گره در هر لحظه صفر است. در گره مرکب، این اصل به ما اجازه میدهد تا با نوشتن معادلهای که مجموع جریانهای واردشونده و خارجشونده را برابر صفر قرار میدهد، جریانهای مجهول را پیدا کنیم. بر خلاف گزینه «کلیه جریانهای عبوری از شاخهها به صورت مستقل اندازهگیری و مستقیما تعیین میشوند» که نادرست است، لازم است معادله تنظیم شود تا مقدار جریانهای مجهول به دست آید. همچنین «اختلاف ولتاژ بین دو انتهای گره» تاثیری در تعیین مستقیم جریانهای ناشناخته ندارد و «استفاده از مقاومت معادل گره» فقط مجموع جریان را ارائه میدهد، نه مقادیر تکتک جریانها. بنابراین «جمع جبری جریانهای ورودی و خروجی و برابر قرار دادن آنها با صفر معادله مورد نیاز برای حل مجهولات ایجاد میشود» روش صحیح است.
۱۸. در چه شرایطی انتخاب روش ترکیبی تحلیل مدار (استفاده همزمان از گره و مش) نسبت به روشهای جداگانه مناسبتر است؟
زمانی که فقط مقاومتهای خطی در مدار وجود داشته باشد.
وقتی تعداد معادلات در روشهای گره یا مش زیاد شود و نیاز به کاهش آن باشد.
وقتی جریان حلقهها فقط از یک جهت عبور کند.
در مواقعی که اختلاف پتانسیل در همه شاخهها ثابت باشد.
استفاده از روش ترکیبی تحلیل مدار زمانی مناسب است که با افزایش پیچیدگی مدار، تعداد معادلات در روشهای گره یا مش به طور جداگانه زیاد شود و حل آنها دشوار گردد. در این شرایط، بهرهگیری همزمان از قوانین جریان کیرشف (KCL) و ولتاژ کیرشف (KVL) باعث کاهش تعداد معادلات و متغیرها و سادهتر شدن تحلیل مدار میشود.













سلام لطفا دیگه رو فیلماتون آهنگ نذاربد.
آقا دقیقا ds چیه؟ زمانه؟پس چرا بردار داره
سلام، وقت شما بخیر؛
خیر ds بردار طول است و ارتباطی به زمان حرکت ذرات در مدار ندارد، به همین دلیل مفهوم دارای برداری است.
اگر در مفهوم کار دقت کنید براساس تعریف کار در فیزیک برابر با حاصلضرب نیرو در جابه جایی است که این مفهوم در مورد کار الکتریکی نیز برقرار است. برای درک بیشتر این موضوع پیشنهاد میکنیم مطلب قضیه کار و انرژی — آموزش سریع و ساده را مطالعه کنید.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
باید بیشتر در مورد هر فرمول توضیح میدادید که هر حرف به چی اشاره داره تو متن من این مورد ندیدم فقط فرمول هارو آورده بودید !!
خیلی عالی ممنون