تحلیل همبستگی کانونی و تفسیر آن | راهنمای کاربردی در SPSS

در آمار، «تجزیه و تحلیل همبستگی کانونی» (CCA)، روشی برای استنباط اطلاعات از ماتریس‌های کوواریانس بین متغیرها است. یک استفاده معمول و کاربردی از همبستگی کانونی، این است که دو مجموعه از متغیرها را در نظر گرفته و ببینید چه چیزی بین این دو مجموعه مشترک است. به عنوان مثال، در آزمایش روانشناسی، می‌توان دو آزمون شخصیت چند بعدی مانند پرسشنامه شخصیت چند مرحله‌ای «مینه سوتا» (MMPI-2) و NEO را انجام داد. با دیدن چگونگی ارتباط عوامل MMPI-2 با عوامل NEO، می‌توان درک کرد که چه ابعادی بین آزمایشات مشترک است و چه مقدار واریانس مشترک بین آن‌ها وجود دارد. به این ترتیب متوجه می‌شویم که یک ویژگی خاص روانی، مقدار قابل توجهی از واریانس مشترک بین این دو آزمون را به خود اختصاص داده است. با توجه به اهمیت موضوع تحلیل همبستگی کانونی و تفسیر آن در محیط SPSS، این نوشتار از مجله فرادرس را به آن اختصاص داده‌ایم.

برای آشنایی بیشتر با ضرایب همبستگی و همچنین نحوه محاسبه آن‌ها در محیط SPSS به نوشتارهای ضریب همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده و تحلیل ضریب همبستگی اسپیرمن در SPSS — از صفر تا صد مراجعه کنید. همچنین خواندن مطالب کوواریانس و نحوه محاسبه آن — به زبان ساده و ضریب همبستگی و ماتریس همبستگی در R — کاربرد در یادگیری ماشین نیز خالی از لطف نیست.

تحلیل همبستگی کانونی و تفسیر آن

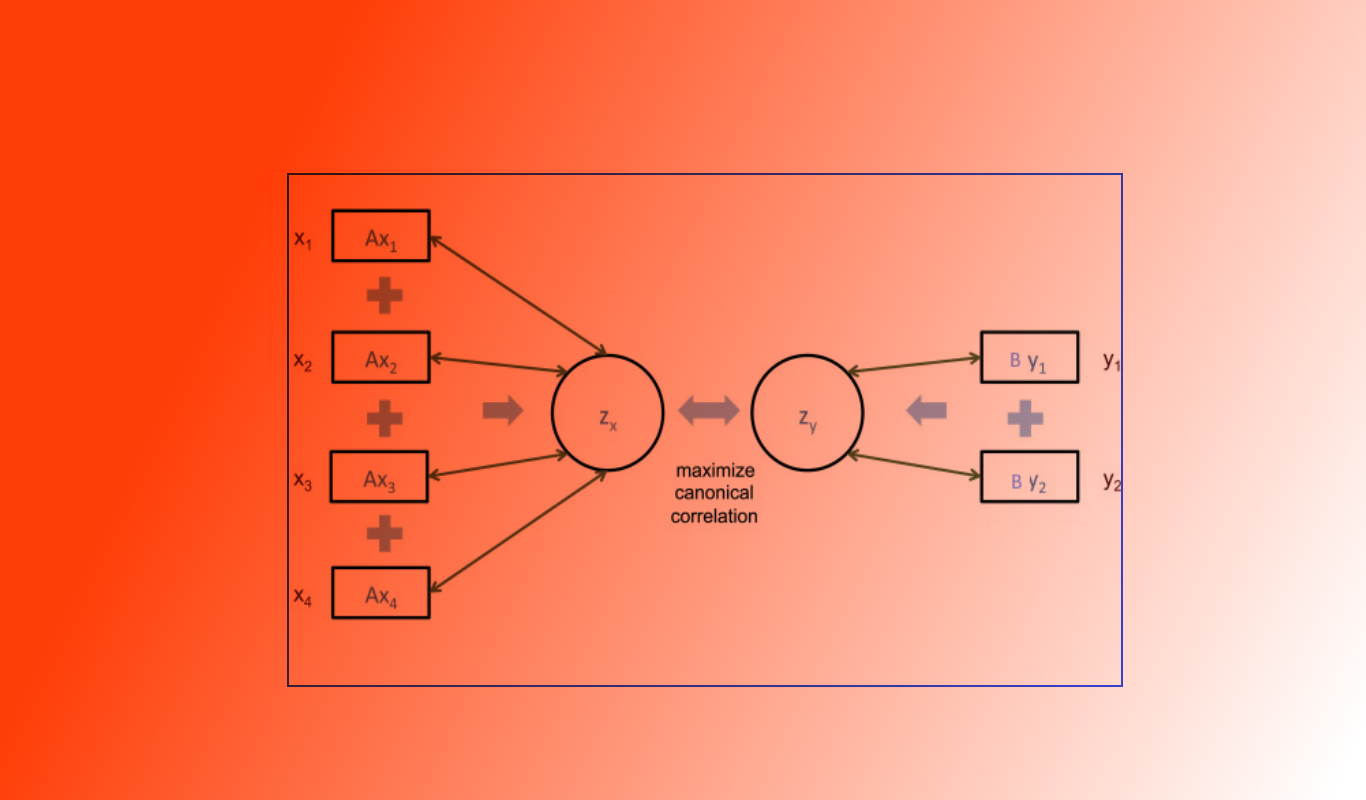
«تجزیه و تحلیل همبستگی کانونی» (Canonical Correlation Analysis) یا به اختصار CCA، یک تحلیل چند متغیره از همبستگی‌ها است. عبارت کانونی، اصطلاحی آماری برای نمایش تحلیل متغیرهای نهفته است که مستقیماً قابل مشاهده یا اندازه‌گیری نیستند. «متغیرهای پنهان» (Latent Variable) به عنوان نماینده متغیرهای متعددی هستند که مشاهده شده و قابل اندازه‌گیری هستند. متغیر پنهان نشانگر ارتباط بین متغیرهای قابل مشاهده است. این اصطلاح را می توان در «تحلیل رگرسیون کانونی» (Canonical Regression Analysis) و در «تحلیل ممیزی چند متغیره» (Multivariate Discriminant Analysis) نیز یافت.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

تجزیه و تحلیل همبستگی، در حقیقت یک آنالیز همبستگی روی متغیر چند بُعدی X و چند بُعدی Y است. ضریب همبستگی کانونی، قدرت یا شدت ارتباط بین این دو متغیر کانونی را اندازه‌گیری می‌کند.

توجه داشته باشید که در اینجا برای هر متغیر چند بُعدی، یک «متغیر کانونی» (Canonical Variate) یا با اختصار CV ساخته می‌شود که مجموع وزنی متغیرها قابل مشاهده در تحلیل است. تحلیل همبستگی کانونی در تحلیل قدرت و شدت ارتباط بین دو سازه نسبت به ضریب همبستگی ساده، ارجح است. این امر به این دلیل است که به کارگیری متغیر کانونی، ساختاری درونی ایجاد می‌کند که برای اندازه‌گیری همبستگی مناسب‌تر است. به عنوان مثال، می‌دانیم که نمره هر درس، اهمیت و ضریب متفاوتی در محاسبه معدل دارد. بنابراین معدل به عنوان یک متغیر پنهان از طریق نمره‌ها و ضرایب اهمیت ساخته شده که می‌توان از آن برای سنجش همبستگی با هوش هیجانی دانش آموزان استفاده کرد. توجه دارید که هوش هیجانی نیز یک متغیر پنهان بوده که توسط ترکیب چندین متغیر دیگر ساخته می‌شود. چنین کاری را در اندازه‌گیری رضایت شغلی و تست استعداد نیز انجام می‌دهند.

این روش برای اولین بار توسط «هارولد هاتلینگ» (Harold Hotelling) در سال 1936 معرفی شد، البته در زمینه زاویه بین طبقه‌ها و مفهوم ریاضی کارهایی توسط جردن (Jordan) در سال 1875 منتشر شد.

تعریف ضریب همبستگی کانونی

دو بردار $$X = (X_1, \ldots, X_n)$$ و $$Y = (Y_1, \ldots, Y_m)$$ از متغیرهای تصادفی که دارای گشتاور دوم متناهی هستند را در نظر بگیرید. به این ترتیب اگر کوواریانس متقابل $$X$$ و $$Y$$ را به صورت زیر نشان دهیم، با یک ماتریس $$n \times m$$ مواجه خواهیم شد که درایه $$(i,j)$$ آن نشانگر کوواریانس $$cov(x_i,y_j)$$ است.

$$\large \Sigma _{XY}=\operatorname {cov} (X,Y)$$

رابطه ۱

آنالیز همبستگی کانونی، به دنبال پیدا کردن برداری‌هایی مثل a ($$a \in R^n$$) و b ($$b \in R^m$$) است که متغیرهای تصادفی $$a^TX , b^TY$$ رابطه همبستگی زیر را حداکثر کنند.

$$\large {\displaystyle \rho =\operatorname {corr} (a^{T}X,b^{T}Y)}$$

رابطه ۲

به این ترتیب متغیرهای تصادفی $$U = a^TX$$ و $$V=b^TY$$ «اولین زوج متغیرهای کانونی» (First Canonical Variate Paired) محسوب می‌شوند.

$$\large {\displaystyle (a',b')={\underset {a,b}{\operatorname {argmax} }}\operatorname {corr} (a^{T}X,b^{T}Y)}$$

رابطه ۳

فیلم آموزش درس رگرسیون 2 – جامع و کاربردی در فرادرس

کلیک کنید

با در نظر گرفتن این دو متغیر و به کارگیری رابطه ۲، سعی می‌شود با تغییر بردارهای $$a$$ و $$b$$، به دو برداری رسید که کمترین میزان وابستگی یا همبستگی را با زوج اول داشته ولی بعد از زوج اول، بیشترین همبستگی را دارند. در این صورت «دومین زوج همبستگی کانونی» (Second Canonical Variate Paired) ساخته می‌شود. این کار را تا مرحله kام که $$k = \min \{m ,n\}$$ می‌توان انجام داد. گاهی به این زوج‌ها، ریشه (Root) نیز گفته می‌شود. بنابراین ریشه اول، نشانگر زوج اول متغیرهای کانونی است. ریشه دوم، زوج دو و الی آخر.

برای مثال اگر همبستگی کانونی بین سه متغیر برای نمرات آزمون و پنج متغیر برای آزمون استعداد را محاسبه کنیم، سه جفت متغیر کانونی یا ریشه استخراج خواهیم کرد.

نکته: توجه داشته باشید که تحلیل همبستگی کانونی، تفاوت عمده‌ای با «تحلیل عاملی» (Factor Analysis) دارد. در تجزیه و تحلیل عوامل، فاکتورها برای به حداکثر رساندن واریانس بین گروه محاسبه می‌شوند در حالی که واریانس درون گروهی را به حداقل می‌رسانند. ولی موضوع در ضریب همبستگی کانونی، حداکثر سازی ضریب همبستگی توسط ترکیب خطی از متغیرهای قابل مشاهده است.

متغیرهای کانونی، یک متغیر عاملی نیستند زیرا فقط اولین جفت متغیر کانونی، متغیرها را به حالتی در می‌آورد که حداکثر همبستگی حاصل می‌شود. زوج دوم، از باقی‌مانده‌های زوج اول ساخته شده به شکلی که بعد از زوج اول، بیشترین همبستگی را دارند.

به این ترتیب نمی‌توان متغیرهای کانونی را به عنوان عامل‌ها در تحلیل عاملی در نظر گرفت. هر چند مشابه تحلیل عاملی، که بارهای عاملی را تشکیل می‌دهیم، در اینجا هم ضرایبی ساخته می‌شوند به گونه‌ای که همبستگی بین ترکیبات خطی، به حداکثر برسد. بنابراین متغیرهای کانونی را نمی‌توان همانند عوامل تحلیل عاملی تفسیر کرد. البته واضح است که متغیرهای کانونی محاسبه شده، به طور خودکار بر یکدیگر عمود یا متعامد هستند، یعنی می‌توان آن‌ها را مستقل از هم در نظر گرفت.

مشابه تحلیل عاملی، نتایج اصلی از آنالیز یا تحلیل همبستگی کانونی شامل، «ضریب همبستگی کانونی» (Canonical Correlations)، «بارهای عامل کانونی» (Canonical Factor Loadings) و «وزن‌های کانونی» (Canonical Weights) است.

از تحلیل همبستگی کانونی، می‌توان برای محاسبه d یا «اندازه افزونگی» (Redundancy Measurement) استفاده کرد.  اندازه افزونگی در «طراحی پرسشنامه» (Questionnaire Design) و «توسعه مقیاس» (Scale Development) اهمیت دارد. به کمک این شاخص می‌تواند به سوالاتی نظیر زیر پاسخ داد.

«وقتی من یک سوال رضایت سنجی با پنج گزینه را از آخرین خرید، ثبت می‌کنم و بعد از خرید، به پاسخ یک سوال سه گزینه‌ای در مورد پشتیبانی می‌رسم، آیا می‌توانم یکی از دو مقیاس را به دلیل کوتاه کردن پرسشنامه خود کنار بگذارم؟»

از نظر آماری، افزونگی، نشان دهنده نسبت واریانس مجموعه‌ای از متغیرها است که با نوع مجموعه دیگری از متغیرها توضیح داده می‌شود. بنابراین اگر این نسبت زیاد باشد، می‌توان یکی از سوالات را حذف کرد.

ضرایب همبستگی متعارف برای وجود روابط کلی بین دو مجموعه از متغیرها به کار رفته و افزونگی اندازه روابط را اندازه‌گیری می‌کند. سرانجام «لاندا ویلک» (Wilk’s lambda) که به صورت U نیز نشان داده می‌شود و «وی بارتلت» (Bartlett’s V) به عنوان آزمون اهمیت ضریب همبستگی کانونی استفاده می‌شوند. به طور معمول از «لاندا ویلک» برای آزمایش اهمیت اولین ضریب همبستگی کانونی و «وی بارتلت»، برای آزمایش اهمیت همه ضرایب همبستگی کانونی مورد بررسی قرار می‌گیرند.

نکته: لطفاً توجه داشته باشید که «تحلیل تشخیصی یا ممیزی» (Analysis Discriminant) یک مورد خاص از تحلیل همبستگی متعارف است. هر «متغیر اسمی» (Nominal Variable) با n سطح متفاوت می‌تواند با n-1 متغیر «دو وضعیتی» (Dichotomous Variables) جایگزین شود. پس تحلیل ممیزی چیزی نیست جز تجزیه و تحلیل همبستگی کانونی مجموعه‌ای از متغیرهای دو وضعیتی با مجموعه‌ای از متغیرهای پیوسته (نسبی یا فاصله‌ای).

محاسبه ضریب همبستگی کانونی

همانطور که گرفته شد، بردارهای $$U$$ و $$V$$، به عنوان اولین زوج متغیرهای کانونی شناخته می‌شوند. اگر $$\Sigma_{UV}$$ ماتریس کوواریانس متقابل (Cross Covariance Matrix) آن‌ها باشد، پارامتری که باید بیشینه شود به صورت زیر خواهند بود.

$$\large {\displaystyle \rho ={\frac {a^{T}\Sigma _{XY}b}{{\sqrt {a^{T}\Sigma _{XX}a}}{\sqrt {b^{T}\Sigma _{YY}b}}}}}$$

رابطه ۴

در اولین گام، پایه‌ها را تغییر می‌دهیم. به این منظور بردارهای $$c$$ و $$d$$ را به صورت زیر تعریف می‌کنیم.

$$\large c= \Sigma_{XX}^{ 1/2}a, \\ \large d= \Sigma_{YY}^{ 1/2}b$$

به این ترتیب رابطه ۴ به صورت زیر درخواهد آمد.

$$\large {\displaystyle \rho ={\frac {c^{T} \Sigma_{XX}^{ -1/2} \Sigma_{XY} \Sigma_{YY}^{ -1/2}d}{{\sqrt {c^{T}c}}{ \sqrt {d^{T} d}}}}}$$

رابطه ۵

به کمک «نامساوی کوشی شوارتز» (Cauchy–Schwarz inequality)، برای رابطه ۵ نامساوی را می‌نویسیم.

$$\large {\displaystyle \left( c^{T}\Sigma_{XX}^{-1/2}\Sigma_{XY}\Sigma_{YY}^{-1/2} \right) (d) \leq \left( c^{T} \Sigma_{XX}^{-1/2} \Sigma_{XY} \Sigma_{YY}^{-1/2}\Sigma_{YY}^{-1/2} \Sigma_{YX} \Sigma_{XX}^{-1/2}c \right)^{1/2} \left( d^{T}d \right)^{1/2}}$$

بنابراین یک کران بالا برای ضریب همبستگی کانونی ساخته می‌شود. به رابطه ۶ توجه کنید.

$$\large {\displaystyle \rho \leq {\frac {\left( c^{T} \Sigma_{XX}^{-1/2} \Sigma_{XY} \Sigma_{YY}^{-1} \Sigma_{YX} \Sigma_{XX}^{-1/2}c \right)^{1/2}}{ \left( c^{T}c \right)^{1/2}}}}$$

رابطه ۶

اگر بردار $$d$$ و $${\displaystyle \Sigma_{YY}^{-1/2} \Sigma_{YX} \Sigma_{XX}^{ -1/2 }c}$$ دارای «همخطی» (Collinear) باشند، نامساوی رابطه ۶ به تساوی تبدیل می‌شود. در ضمن اگر بردار $$c$$، همان بردار ویژه با بزرگترین مقدار ویژه ماتریس $${\displaystyle \Sigma _{XX}^{-1/2}\Sigma _{XY}\Sigma _{YY}^{-1}\Sigma _{YX}\Sigma _{XX}^{-1/2}}$$ باشد، حداکثر ضریب همبستگی در رابطه ۶، حاصل خواهد شده و اولین زوج متغیرهای کانونی بدست می‌آید.

نکته: برای پیدا کردن زوج‌های بعدی متغیرهای کانونی، کافی است مقادیر ویژه کوچکتر را به ترتیب لحاظ کرده و مقادیر ضریب همبستگی را بدست آورد.

شیوه دیگر برای بدست آوردن ضریب همبستگی کانونی، در نظر گرفتن بردارهای $$c$$ و $$d$$ براساس بردارهای منفرد یا تکین راست و چپ (Left , Right Singular Vectors) ماتریس همبستگی بین متغیرهای $$X$$ و $$Y$$ است که بیشترین مقدار منفرد را دارند. این شیوه محاسباتی در ادامه دیده می‌شود.

بردارهای منفرد و محاسبه ضریب همبستگی کانونی

طبق توضیحاتی که در قسمت قبل ارائه شد، گام‌ها و مراحل زیر را برای پیدا کردن همبستگی کانونی طی می‌کنیم.

• بردار $$c$$ را «مقادیر ویژه» (Eigen Value) ماتریس زیر در نظر می‌گیریم.

$$\large {\displaystyle \Sigma_{XX}^{-1/2} \Sigma_{XY}\Sigma_{YY}^{-1} \Sigma_{YX} \Sigma_{XX}^{-1/2}}$$

• بردار $$d$$ را متناسب با بردار زیر قرار می‌دهیم.

$$\large {\displaystyle \Sigma_{YY}^{-1/2} \Sigma_{YX}\Sigma_{XX}^{-1/2}c}$$

• به طور عکس، بردار $$d$$ را بر اساس «بردار ویژه» (Eigen Vector) ماتریس زیر مشخص می‌کنیم. به تغییر متغیر $$X$$ به $$Y$$ دقت کنید.

$$\large {\displaystyle \Sigma_{YY}^{-1/2} \Sigma_{YX} \Sigma_{XX}^{-1} \Sigma_{XY} \Sigma_{YY}^{-1/2}}$$

• از طرفی بردار $$c$$ را هم متناسب با بردار زیر می‌سازیم.

$$\large {\displaystyle \Sigma_{XX}^{-1/2} \Sigma_{XY} \Sigma_{Y Y}^{-1/2}d}$$

• مقدار ویژه ماتریس زیر را $$a$$ می‌نامیم.

$$\large {\displaystyle \Sigma_{XX}^{-1} \Sigma_{XY}\Sigma_{YY}^{-1}\Sigma _{YX}}$$

• بردار $$b$$ را متناسب با بردار زیر در نظر می‌گیریم.

$$\large {\displaystyle \Sigma_{YY}^{-1} \Sigma_{Y X}a}$$

• حالا مراحل را برعکس کرده و $$b$$ را بردار ویژه ماتریس زیر فرض می‌کنیم.

$$\large {\displaystyle \Sigma_{YY}^{-1} \Sigma_{YX} \Sigma_{XX}^{-1} \Sigma_{XY}}$$

• و بردار $$a$$ را متناسب با بردار زیر، می‌سازیم.

$$\large {\displaystyle \Sigma_{XX}^{-1} \Sigma_{XY} b}$$

به این ترتیب متغیرهای کانونی $$U$$ و $$V$$ به صورت زیر محاسبه می‌شوند.

$$\large {\displaystyle U=c' \Sigma_{X X}^{-1/2} X =a'X} \\ \large {\displaystyle V=d' \Sigma_{Y Y}^{-1/2} Y= b'Y}$$

یک مثال محاسباتی ساده

فرض کنید متغیر تصادفی $$X= x$$ دارای میانگین یا امید ریاضی $$E(X)=0$$ باشد. اگر متغیر تصادفی $$Y$$ را به صورت $$Y=X$$ تعریف کنیم، بردارهای $$a$$ و $$b$$، یک ستون از مقدار ۱ را تشکیل می‌دهند. بنابراین اولین زوج متغیرهای کانونی به صورت $$U=V$$ ساخته شده که در آن $$V=U=X$$ است. توجه دارید که در این حالت، همبستگی کامل و مثبت بین $$X$$ و $$Y$$ وجود دارد.

اگر $$Y=-X$$ باشد، همبستگی کامل ولی معکوس است. به این ترتیب $$a=1, b = -1$$ خواهد بود. پس، اولین زوج متغیرهای کانونی به شکل $$U=X$$ و $$V = -Y=X$$ ساخته می‌شوند. واضح است که در هر دو وضعیت (همبستگی کامل مثبت و معکوس)، $$U=V$$ است. این موضوع نشان می‌دهد که تحلیل همبستگی کانونی، شبیه ضریب همبستگی بین متغیرها عمل کرده است.

محاسبه ضریب همبستگی کانونی در SPSS

خوشبختانه، محاسبه رابطه‌های گفته شده، توسط بسیاری از نرم‌افزارهای محاسباتی و آماری نظیر متلب (Matlab)، سَس (SAS) و اس پی اس اس (SPSS) انجام می‌شود. در بخش بعدی، شیوه محاسبه ضریب همبستگی کانونی را با ارائه یک مثال در محیط SPSS شرح می‌دهیم.

تحلیل همبستگی متعارف در SPSS

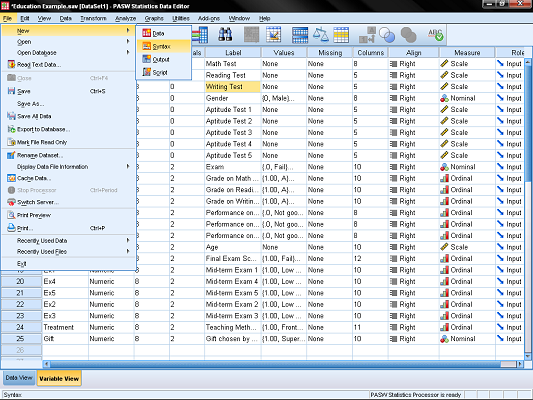
فرض کنید فایل اطلاعاتی مانند تصویر ۱، در اختیار داریم. قرار است بین گروه متغیرهای آزمون ریاضی (Math Test) با نام Test_Scoreو خواندن (Reading Test) با نام Test2_Score و نوشتن (Writing) با نام Test3_Score و گروه متغیرهای استعداد سنجی ۱ تا ۵ (که با Apt1 ت Apt5 مشخص شده‌اند) یک تحلیل همبستگی اجرا کنیم. به بیان دیگر می‌خواهیم قدرت ارتباط بین پنج آزمون استعداد و سه آزمون ریاضی، خواندن و نوشتن را نشان دهیم. داده‌ها و مقادیر این فایل داده‌ها را می‌توانید براساس شبیه‌سازی ایجاد کنید. از آنجایی دسترسی به محتوای اصلی اطلاعات مقدور نیست، فقط به معرفی متغیرها و نحوه اجرا و تفسیر نتایج خواهیم پرداخت.

فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS در فرادرس

کلیک کنید

متأسفانه، SPSS، فهرستی برای تجزیه و تحلیل همبستگی کانونی ندارد. ولی نگران نباشید به کمک نوشتن چند دستور، تحلیل مورد نظر اجرا خواهد شد. بنابراین ما چند دستور را در پنجره Syntax وارد کرده و آن‌ها را اجرا می‌کنیم. نگران نباشید، شاید کد نویسی به نظر پیچیده برسد ولی خوانایی دستورات نوشته شده به شما کمک می‌کند که مراحل را بهتر درک کنید. ابتدا باید پنجره Syntax را باز کنیم. برای انجام این کار از مسیر زیر اقدام کنید.

File - New - Syntax

ما باید از دستور MANOVA و زیر فرمان discrim/ در یک طرح تک عاملی کمک بگیرم. ابتدا تمام متغیرهای مستقل را در یک هر گروه و متغیرهای وابسته را در گروه دیگر مشخص می‌کنیم. این کار به واسطه پارامتر WITH انجام می‌شود. لیست متغیرهای دستور MANOVA ابتدا متغیرهای وابسته و متغیرهای مستقل را دنبال می‌کند (لطفاً به جای WITH از دستور BY استفاده نکنید زیرا این امر باعث جدا شدن فاکتورها مانند تجزیه و تحلیل MANOVA می‌شود).

به تصویر 2، که نمایانگر پنجره کد نویسی و دستورات لازم برای تحلیل همبستگی کانونی است توجه کنید.

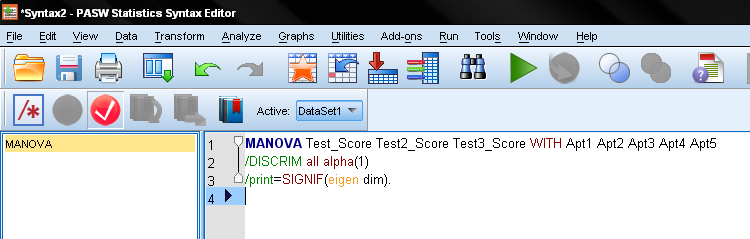
زیرفرمان  discrim/ یک تحلیل همبستگی کانونی برای همه متغیرها همبسته (Covariate) ایجاد می‌کند. متغیرها همبسته یا مستقل پس از کلمه کلیدی WITH مشخص شده‌اند. ALPHA سطح با معنایی مورد نیاز قبل از استخراج متغیر کانونی را مشخص می‌کند، پیش فرض 0٫25 است. ولی ما آن را روی 1٫0 تنظیم کرده‌ایم تا تمام توابع تشخیصی گزارش شوند. واضح است که حدود تغییرات برای مقدار ALPHA، در بازه ۰ تا ۱ خواهد بود.

برای اجرای کد، خطوط مختلف آن را انتخاب کرده و با استفاده از دکمه Run، از نوار ابزار، آن‌ها را اجرا کنید. دسترسی به دستور RUN و انتخاب کد در تصویر ۳ دیده می‌شود.

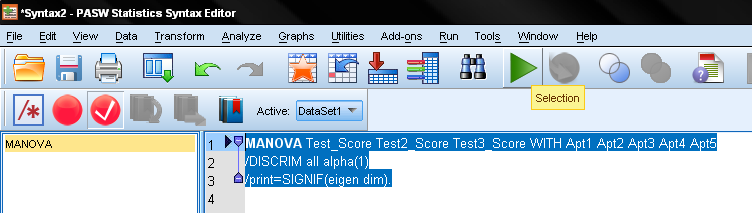
تفسیر خروجی تحلیل همبستگی کانونی

دستورات مربوط به تصویر ۳، خروجی مفصلی و طولانی در پنجره Output نرم‌افزار SPSS ایجاد می‌کند. در این بخش می‌خواهیم در مورد هر یک از جدول‌های تولید شده، بحث کرده و هر یک از مقادیر را معرفی کنیم.

خروجی با توصیف نمونه (sample description) شروع می‌شود که تعداد مشاهدات و داده‌های گمشده و معتبر را نشان می‌دهد. از آنجایی می‌خواهیم هدف و تمرکز را روی تحلیل همبستگی کانونی قرار دهیم، از نمایش جدول‌های نامرتبط مانند توصیف نمونه، صرف نظر خواهیم کرد.

در جدول بعدی، با نام (Analysis of Variance -- Design 1)، برازش کلی مدل، گزارش شده و شاخص‌هایی نظیر معیارهای چند متغیره Pillais ،Hotellings ،Wilk و Roys نشان داده شده است. آزمون آماری که معمولاً مورد استفاده قرار می‌گیرد براساس آماره «لاندا ویلک» (Wilk’s lambda) است، اما در می‌یابیم که همه معیارها به کار رفته برای آزمون در سطح خطای ۰٫۰۵ معنی دار هستند زیرا داریم p <0٫05. البته توجه دارید که «پی-مقدار» (p-Value) در SPSS به صورت Sig در تصویر ۴ نشان داده می‌شود.

آزمون‌های صورت گرفته نشانگر آن است که مدل به خوبی برازش شده و ارتباط بین متغیرهای کانونی برقرار است. در بخش بعدی ضرایب همبستگی کانونی و مقادیر ویژه ریشه‌های کانونی گزارش می‌شوند. اولین ضرایب همبستگی کانونی و مقادیر ویژه ریشه‌های کانونی در تصویر ۵ قابل مشاهده‌اند.

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس

کلیک کنید

اولین زوج متغیر کانونی (Root No) برابر با مقدار 0٫81108 است که با یک درصد مناسب یعنی 96٫87٪ از همبستگی کل دیده می‌شود.  مقدار ویژه 1٫92265 برای این متغیر کانونی بدست آمده است. بنابراین این جدول نشان می‌دهد که فرضیه ما که وجود ارتباط بین دو دسته متغیر را در نظر گرفته بود، درست است و فرض صفر رد می‌شود. به طور کلی نمرات آزمون استاندارد و نمرات آزمون استعدادیابی با هم ارتباط مثبت دارند.

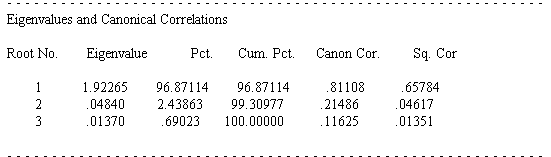
تاکنون خروجی فقط تناسب کلی مدل را نشان داد. قسمت بعدی (تصویر ۶) اهمیت هر یک از ریشه‌ها را مورد آزمایش قرار می‌دهد. مشخص است که از سه ریشه ممکن، فقط ریشه اول با p <۰٫05 معنی دار است. از آنجا که مدل ما شامل سه نمره آزمون (ریاضی، خواندن، نوشتن) و پنج آزمون استعداد است، SPSS سه ریشه استخراج کرده است که فقط در اولین سطر مقدار Sig آن از ۵٪ کمتر است.

اولین آزمون معنی‌داری هر سه ریشه کانونی را آزمون کرده و نتیجه را معنی‌دار می‌کند. آزمون دوم، ریشه اول را حذف و ریشه دو تا سه را آزمون می‌کند که فرض صفر رد نشده و بی‌معنی بودن متغیرهای کانونی دو و سوم را نشان می‌دهد. در سطر آخر نیز فرض بی‌معنی بودن آماری متغیر کانونی سوم، رد نخواهد شد. بنابراین در مثال ما فقط اولین ریشه معنی دار است زیرا برای آن داریم p <۰٫05.

در بخش‌های بعدی خروجی، نرم‌افزار SPSS نتایج را به طور جداگانه برای هر یک از دو مجموعه متغیر ارائه می‌دهد. در هر مجموعه، SPSS ضرایب کانونی خام، ضرایب استاندارد شده، همبستگی بین متغیرهای مشاهده شده، متغیرهای کانونی و درصد واریانس توضیح داده شده توسط متغیر کانونی را محاسبه کرده در جدول با عنوان EFFECT..Within CELLS Regression نشان می‌دهد. در زیر نتایج 3 متغیر آزمون ریاضی (Test_Score)، خواندن (Test2_Score) و نوشتن (Test3_Score) آورده شده است. به تصویر ۷، توجه کنید.

ضرایب کانونی خام مشابه ضرایب در رگرسیون خطی هستند. از آنها می‌توان برای محاسبه نمرات کانونی استفاده کرد. ولی اهمیت آن‌ها با توجه به مقیاس، ممکن است تغییر کند. ضرایب استاندارد، اهمیت این متغیرها را بدون در نظر مقیاس اندازه‌گیری آن‌ها مشخص می‌کند. در جدول زیر (تصویر ۸) برای سه متغیر اصلی برای نمره آزمون ریاضی، خواندن و نوشتن، هر یک از ضرایب کانونی خام محاسبه شده است.

ضرایب استاندارد شده برای تفسیر آسان‌تر به کار می‌روند، توجه داشته باشید که در این حالت میانگین صفر و انحراف استاندارد برابر با ۱ است. با توجه به تصویر 6، فقط ریشه اول معنی‌دار بوده و ریشه‌های دوم و سوم قابل توجه یا معنی‌دار محسوب نمی‌شوند. قوی‌ترین تأثیر در اولین ریشه، متغیر Test_Score است (که نمره ریاضی را نشان می‌دهد). در تصویر ۹، ضرایب استاندارد کانونی را مشاهده می‌کنید.

جدول مربوط به تصویر ۱۰، همبستگی بین متغیرهای وابسته و متغیرهای کانونی را نشان می‌دهد. مشخص است که بیشترین وابستگی برای متغیر کانونی اول، براساس متغیر آزمون خواندن (و به صورت معکوس) بوده. همچنین بیشترین ارتباط بین متغیر کانونی دوم با متغیر آزمون نوشتن دیده می‌شود. از طرفی متغیر کانونی سوم با متغیر نمره ریاضی بیشترین همبستگی را دارد.

در آخرین بخش از خروجی، متغیرهای کانونی و خصوصیات هر یک از آن‌ها نمایش داده می‌شود. در ستون Can Var، شماره متغیر کانونی، در ستون Pct Var DEP سهمی که متغیر کانونی در بیان واریانس متغیر وابسته ایفا کرده، دیده می‌شود. ستون‌های بعدی Cum Pct Dep، درصد تجمعی برای ستون قبلی قرار دارد.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

همچنین سهم یا درصد از واریانس متغیر همبسته در ستون Pct Var COV و درصد تجمعی (Cum Pct COV) دیده می‌شود. به تصویر ۱۱ توجه کنید. سهم متغیر کانونی اول، هم در واریانس متغیر وابسته و هم متغیر همبسته (Covariate) بیشتر از متغیرهای کانونی دوم و سوم است.

همانطور که دیدید، یک دستور و یک خط زیرفرمان در SPSS، خروجی مفصل و کاملی از آنالیز یا تحلیل همبستگی کانونی ایجاد می‌کند. شاخص‌های ارائه شده، به تحلیل مناسب کمک کرده و باعث می‌شود، محقق قادر باشد با شیوه‌های مختلف، نتیجه حاصل را تفسیر یا مقایسه کند.

خلاصه و جمع‌بندی

همانطور که در این نوشتار خواندید، ضریب همبستگی کانونی، براساس ترکیب خطی از چند متغیر به عنوان گروه اول، و ترکیب خطی از دیگر متغیرها، ساخته و محاسبه می‌شود. بطوری که زوج متغیرهای کانونی اول، بیشترین همبستگی بین این دو ترکیب خطی را مشخص می‌کند. البته می‌توان با توجه به ابعاد هر یک از متغیرها، تعداد زوج متغیرهای کانونی بیشتری را مشخص کرد، ولی سهم هر یک از این زوج‌ها از همبستگی کل، کاهشی است و در زوج‌های دوم و سوم و ...، مقدار ضریب همبستگی کانونی کاسته می‌شود. از آنجایی که در تحلیل پرسشنامه‌ها و سوالات و همچنین روایی، از ضریب و تحلیل همبستگی کانونی نیز می‌توان استفاده کرد، فراگیری این شاخص اهمیت پیدا می‌کند.