فرادرسبرش ساده — آشنایی با خصوصیات رفتاری مواد
«برش ساده» (Simple Shear)، نوعی تغییر شکل است که در طی آن صفحات موازی درون جسم به صورت موازی باقی می‌مانند و فاصله خود را با یکدیگر حفظ می‌کنند اما نسبت به هم جابجا می‌شوند.
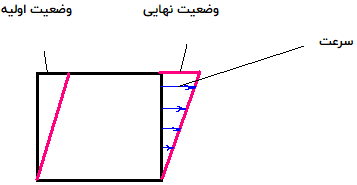
برش ساده در سیالات
در مکانیک سیالات، برش ساده یکی از حالت‌های بخصوص تغییر شکل محسوب می‌شود.
در این تغییر شکل، تنها یکی از مؤلفه‌های بردار سرعت دارای مقداری غیر صفر است:
$${\displaystyle V_{x}=f(x,y)}$$
$${\displaystyle V_{y}=V_{z}=0}$$
به این ترتیب، گرادیان سرعت مقداری ثابت و عمود بر بردار سرعت خواهد بود:
$${\frac {\partial V_{x}}{\partial y}}={\dot {\gamma}}$$
در معادله بالا، ˙γ، نرخ برش در جهت y را نشان می‌دهد. نرخ برش در جهات دیگر نیز عبارت است از:
$${\frac {\partial V_{x}}{\partial x}}={\frac {\partial V_{x}}{\partial z}}=0$$
تانسور گرادیان جابجایی (Γ) برای این نوع تغییر شکل، تنها دارای یک عبارت غیر صفر است:
$$\Gamma ={\begin{bmatrix}0&{\dot {\gamma }}&0\\ 0&0&0\\ 0&0&0\end{bmatrix}}$$
برش ساده با نرخ ˙γ (عبارت 1)، از حاصل جمع کرنش برشی خالص با نرخ γ˙/2 (عبارت 2) و دوران با نرخ γ˙/2 (عبارت 3) به دست می‌آید:
$${\displaystyle \Gamma ={\begin{matrix}{\begin{bmatrix}0&{\dot {\gamma }}&0\\0&0&0\\0&0&0\end{bmatrix}} \\{\mbox{(1)}}\end{matrix}}={\begin{matrix}{\begin{bmatrix}0&{{\tfrac {1}{2}}{\dot {\gamma }}}&0\\{{\tfrac {1}{2}}{\dot {\gamma }}}&0&0\\0&0&0\end{bmatrix}} \\{\mbox{(2)}}\end{matrix}}+{\begin{matrix}{\begin{bmatrix}0&{{\tfrac {1}{2}}{\dot {\gamma }}}&0\\{-{{\tfrac {1}{2}}{\dot {\gamma }}}}&0&0\\0&0&0\end{bmatrix}} \\{\mbox{(3)}}\end{matrix}}}$$
از نمونه‌های کاربرد برش ساده در مسائل مختلف می‌توان به دو مورد مهم اشاره کرد؛ عبور جریان آرام از درون لوله‌های بلند با سطح مقطع ثابت که با عنوان «جریان پویزل» (Poiseuille flow) شناخته می‌شود و «بالشتک‌های الاستومری زیر سری پل» (Elastomeric Bearing Pads) در سیستم‌های جداسازی پایه که برای جلوگیری از آسیب سازه‌های مهم در مواجه زلزله مورد استفاده قرار می‌گیرند.
برش ساده در جامدات
در مکانیک جامدات، برش ساده یک تغییر شکل صفحه‌ای با حجم ثابت است که در طی آن، هیچ تغییری در طول و امتداد مجموعه المان‌های خطی با جهت‌گیری مرجع رخ نمی‌دهد. وجود چرخش صلب در این نوع تغییر شکل، سبب تمایز آن با برش خالص می‌شود.
اگر e1، جهت‌گیری مرجع (ثابت) برای المان‌های خطیِ بدون تغییر در حین تغییر شکل و e1-e2، صفحه تغییر شکل باشد، گرادیان تغییر شکل در برش ساده به صورت زیر تعریف خواهد شد:
$${\displaystyle {\boldsymbol {F}}={\begin{bmatrix}1&\gamma &0\\ 0&1&0\\ 0&0&1\end{bmatrix}}}$$
به صورت دیگر می‌توان نوشت:
$${\displaystyle {\boldsymbol {F}}={\boldsymbol {\mathit {1}}}+\gamma \mathbf {e} _{1}\otimes \mathbf {e} _{2}}$$
از میله تحت پیچش می‌توان به عنوان یکی از مثال‌های کاربردی برای جسم تحت برش ساده نام برد. برای مواد لاستیکی، رفتار تنش-کرنش در هنگام تغییر شکل برش ساده تقریباً خطی است.
رابطه بین تنش و کرنش برشی ساده
معادله زیر، رابطه بین تنش برشی (τ) و کرنش برشی (γ) را نشان می‌دهد:
$$\tau = \gamma G\,$$
G: مدول برشی
$$G = \frac{E}{2(1+\nu)}$$
E: مدول یانگ؛ ν: نسبت پواسون
$$\tau = \frac{\gamma E}{2(1+\nu)}$$
امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به فراگیری موضوعات مشابه علاقه‌مند هستید، آموزش‌های زیر را به شما پیشنهاد می‌کنیم:
- مجموعه آموزش های مهندسی عمران
- آموزش مقاومت مصالح
- مجموعه آموزش‌های دروس مهندسی مکانیک
- مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد
^^
