تحلیل شبکه های اجتماعی (Social Network Analysis) — به زبان ساده و جامع

«شبکه اجتماعی» (Social Network)، ساختاری اجتماعی متشکل از بازیگران شبکه (برای مثال اشخاص یا سازمان‌ها) و روابط میان آن‌ها است. در واقع باید گفت شبکه‌های اجتماعی از «گره‌ها» (Nodes) و «یال‌ها» (Edges) تشکیل شده‌اند. از گره‌ها با عنوان راس نیز یاد می‌شود. شاید بتوان گفت قدمت شبکه‌های اجتماعی به شکل‌گیری اولین اجتماعات انسانی باز می‌گردد. پژوهش‌ها در این حوزه نیز عمری طویل داشته و از سال ۱۸۲۰ با تلاش‌های «دیوید امیل دورکیم» (David Émile Durkheim) و «فردیناند تونیس» (Ferdinand Tönnies) به طور جدی آغاز شدند.

جنس دیگری از شبکه‌های اجتماعی با ظهور وب ۲.۰ پا به عرصه وجود گذاشت که به آن‌ها «شبکه‌های اجتماعی برخط» (Online Social Networks | OSN) گفته می‌شود. چنین شبکه‌های اجتماعی بر پایه وب بنا شده‌اند و از جمله آن‌ها می‌توان به «آیدنتیکا» (identi.ca)، «توییتر» (Twitter)، «گوگل پلاس» (+Google)، «فیس‌بوک» (Facebook)، «لینکدین» (LinkedIn)، «یوتیوب» (Youtube)، «اینستاگرام» (Instagram) و «ساوندکلاود» (SoundCloud) اشاره کرد.

این شبکه‌های اجتماعی جهان واقعی با داده‌های مربوط به انسان‌ها - که معمولا توسط ایشان تولید می‌شوند - و اغلب در برگیرنده مشخصه‌های اجتماعی آن‌ها هستند توسعه پیدا می‌کنند. تحلیل شبکه‌های اجتماعی (Social Network Analysis | SNA) فرآیند تحقیق و بررسی ساختارهای اجتماعی با استفاده از «نظریه شبکه» (Network Theory) و «نظریه گراف» (Graph Theory) است.

فیلم آموزش تحلیل شبکه های اجتماعی با زبان R و متن کاوی Text Mining در فرادرس

کلیک کنید

به عنوان مثالی از تحلیل شبکه‌های اجتماعی می‌توان به بررسی الگوهای موجود در گراف شبکه اشاره کرد که براساس آن می‌توان به دانشی پیرامون الگوهای رفتاری انسان‌ها و در نتیجه اطلاعات ارزشمند قابل تحلیل و کاوش درباره نوع بشر دست پیدا کرد. نتایج حاصل از تحلیل شبکه‌های اجتماعی در برگیرنده ارزش و قدرتی است که توسط بسیاری از سازمان‌ها و شرکت‌های (کوچک، متوسط و بزرگ) دولتی و خصوصی برای بیشینه‌سازی بازده مورد استفاده قرار می‌گیرد.

اغلب انسان‌ها از «رسانه‌های اجتماعی» (Social Media) به منظور یافتن شغل، بیان دیدگاه‌ها، دوست‌یابی، در ارتباط بودن با دیگران، بازی کردن و بسیاری از اهداف دیگر استفاده می‌کنند. همچنین، دامنه کاربردهای سایت‌های اجتماعی به این موارد محدود نشده و چنین شبکه‌هایی در حال حاضر به شدت تصمیم‌گیری‌های کسب‌و‌کارها برای بازاریابی و فروش، مدیریت زنجیره تامین و تبلیغات را با دانش تحلیل شبکه تحت تاثیر قرار داده‌اند.

شبکه‌های اجتماعی برخط شبکه‌های تصادفی نیستند که گره‌ها (بازیگران) در آن‌ها به طور تصادفی اضافه شوند، بلکه دارای ویژگی‌های خاص و بعضا منحصر به فردی هستند. پرسشی که در این وهله مطرح می‌شود این است که این ویژگی‌ها چه هستند؟ در ادامه به این ویژگی‌ها و چگونگی تحلیل شبکه‌های اجتماعی برخط با استفاده از آن‌ها پرداخته می‌شود.

اتصال

آیا گراف‌های اجتماعی بزرگ مقیاس و جهان واقعی متصل (connected) هستند؟ بلی، حتی اگر این گراف‌ها به طور کامل نیز متصل نباشند احتمال وجود مواردی که متصل نیستند بسیار کم است.

فیلم آموزش تحلیل شبکه های اجتماعی با نرم افزار نود ایکس ال NodeXL در فرادرس

کلیک کنید

برای درک بهتر مفهوم متصل بودن گراف شبکه‌های اجتماعی، شرایطی را می‌توان در نظر گرفت که ۵۰ دانش‌آموز یک کلاس هر یک ۳ دوست دارند. احتمال آنکه گراف حاصل از نمونه بیان شده غیر متصل باشد چقدر است؟

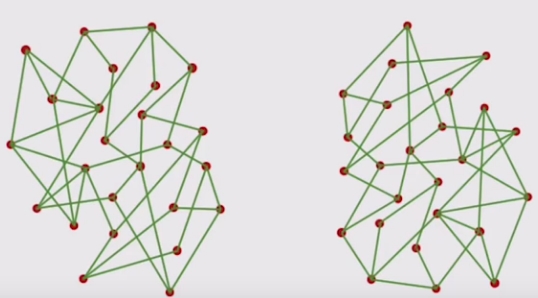
این مثال از یک کلاس کوچک بود، تصور کنید که این محاسبات برای یک شبکه بسیار بزرگ انجام شود. اگر به ریاضیات نهفته در پس این گراف‌ها نگاه شود امکان دارد غیر متصل باشند، اما وقوع چنین مساله‌ای برای شبکه‌های جهان واقعی بسیار غیر محتمل است. ویژگی «اتصال» (Connectedness) را می‌توان با توجه به مساله مطرح شده در ادامه تحلیل کرد. n گره (از یک گراف) داده شده است، حداقل تعداد یال‌هایی که باید به گراف کاملا غیر متصل اضافه شوند تا گراف ذاتا متصل شود چندتا است؟

فیلم آموزش تحلیل شبکه های اجتماعی با نرم افزارهای گفی Gephi و پاژک Pajek در فرادرس

کلیک کنید

پرسش دیگر آن است که آیا زمانی که یک گراف هیچ راس (vertex) ایزوله‌ای ندارد، یال‌های موجود به طور یکنواخت و تصادفی قرار گرفته‌اند؟ اگر مساله مطرح شده با «تحلیل احتمالات» (Probabilistic Analysis) حل شود، نتیجه به شرح زیر است: اگر (n*log(n یال قرار داده شود، احتمال آنکه این گراف غیر متصل باشد $$(1/n)^2$$ است. مقدار n در شبکه‌های جهان واقعی بسیار بزرگ و در نتیجه وقوع غیر متصل بودن غیرمحتمل است. اما مفهوم واقعی ویژگی اتصال (Connectedness) چیست؟

مفهوم ویژگی اتصال

بسیاری از افراد این روزها نام «کمبریج آنالیتیکا» (Cambridge Analytica) را شنیده‌اند. در مارس ۲۰۱۸، «نیویورک تایمز» (The New York Times) و «آبزرور» (The Observer) گزارشی مبنی بر اینکه شرکت سهامی خاص کمبریج آنالیتیکا بدون کسب اجازه از اطلاعات شخصی افرادی که با اهداف آکادمیک گردآوری شده بود در کمپین‌های سیاسی استفاده کرده ارائه دادند.

فیلم آموزش تحلیل شبکه های اجتماعی با زبان R و متن کاوی Text Mining در فرادرس

کلیک کنید

اما کمبریج آنالیتیکا واقعا چه کرده بود؟ جریان از این قرار بود که «الکساندر کوگان» (Aleksandr Kogan)، از اساتید روان‌شناسی «دانشگاه کمبریج» (University of Cambridge) به منظور انجام یک پژوهش آکادمیک در سال ۲۰۱۴، یک برنامه تست شخصیت در فیس‌بوک طراحی می‌کند و بالغ بر ۲۷۰ هزار کاربر آمریکایی فیس‌بوک به صورت داوطلبانه از آن استفاده می‌کنند.

کوگان با بهره‌گیری از این داده‌ها و ویژگی‌های مربوط به تحلیل شبکه‌های اجتماعی موفق به گردآوری داده‌های مربوط به دوستان افراد شرکت‌کننده در تست نظرسنجی نیز می‌شود و بدین شکل حجم زیادی از داده‌ها پیرامون جمعیت بالایی از کاربران فراهم می‌شود. کوگان در نهایت این داده‌ها را به شرکت کمبریج آنالیتیکا می‌فروشد و آن‌ها از این داده‌ها در کمپین‌های تبلیغاتی سیاسی انتخابات سال ۲۰۱۶ آمریکا بهره بردند. اما کوگان و کمبریج آنالیتیکا چگونه توانستند از داده‌های شرکت‌کنندگان در نظرسنجی به داده‌های دوستان آن‌ها دست یابند؟

با توجه به فرض مطرح شده که شبکه دوستی ایالات متحده آمریکا در فیس‌بوک متصل است، با بهره‌گیری از یک «حفره» (loophole) در «رابط کاربردی برنامه‌نویسی» (Application Programming Interface) آن‌ها توانسته بودند به اطلاعات خام ۸۷ میلیون نفر با تحلیل اطلاعات دوستانشان که در آزمون کوگان شرکت کرده بودند دست پیدا کنند.

صرفا برای اینکه مقیاس تاثیر این جریان شفاف شود، باید گفت در این آزمون ۲۷۰۰۰۰ کاربر شرکت کرده بودند که موجب شد کمبریج آنالیتیکا بتواند به ۳۲۲ برابر اطلاعات افراد دست پیدا کند. ویژگی که منجر به دستیابی به اطلاعات دوستانِ دوستان و زنجیره انسانی موجود در شبکه‌های اجتماعی شد. این یعنی آنالیتیکا توانسته بود به اطلاعات ۲۷٪ از جمعیت آمریکا تنها با یک آزمون ساده دست پیدا کند. اکنون می‌توان داده‌هایی که غول‌های فناوری در اختیار دارند و قدرتی که با تحلیل داده‌های شبکه‌های اجتماعی به دست می‌آورند را متصور شد.

در ادامه نگاهی اجمالی به این بحث و تحلیل‌های مربوط به آن انداخته خواهد شد. این داده‌ها به چه شکل یا فرمی وجود دارند؟ همانطور که پیش‌تر بیان شد، داده‌های شبکه‌های اجتماعی به صورت گراف‌هایی با گره‌ها و یال‌ها ذخیره و مصورسازی می‌شوند و هر یک از آن‌ها ویژگی‌های خاصی را از خود بروز می‌دهد. اکنون، اشکال گوناگونی که این داده‌ها ارائه می‌شوند مورد بررسی قرار خواهد گرفت.

مجموعه داده‌های گراف

در ادامه فرمت‌های گوناگونی که مجموعه داده‌های شبکه‌های اجتماعی برای تحلیل موجود هستند مورد بررسی قرار می‌گیرد.

فیلم آموزش نظریه گراف و کاربردها در فرادرس

کلیک کنید

فرمت CSV: داده‌ها به صورت «فهرست یال» (Edgelist) یا «فهرست همسایگی» (Adjacency List) ارائه می‌شوند. فرمت Edgelist شامل دو/سه مقدار در هر خط است ([To, From, [Weight). گره‌ها اطلاعاتی پیرامون یال‌هایی که در گراف وجود دارند با هر وزنی که به آن‌ها داده شده به دست می‌دهند. در این فرمت، اولین مقدار در یک سطر گره منبع و در ادامه گره‌هایی هستند که یال‌ها به آن‌ها متصل می‌شوند، برای مثال [... ,Source, Node1, Node2].

فرمت GML: یکی از متداول‌ترین فرمت‌هایی است که انعطاف‌پذیری بالایی برای ذخیره‌سازی اطلاعات دارد. GML یک زبان مدل‌سازی برای ذخیره‌سازی اطلاعات پیرامون گره‌ها، یال‌ها، برچسب‌ها، خصیصه‌ها (ویژگی‌ها) و دیگر موارد است.

فرمت Pajek Net: این فرمت از افزونه NET. استفاده می‌کند. دو ستون در این فرمت ارائه شده‌اند، یکی راس‌ها که برچسب گره‌ها را تعیین می‌کند و دیگری یال‌های بین گره‌ها را نشان می‌دهد. اگر گره‌ها هیچ برچسبی نداشتند، ورودی‌های سطرها زیر ستون راس‌ها قابل چشم‌پوشی است. همچنین، مقدار یک خصیصه در صورت نیاز قابل اضافه شدن است.

۴. فرمت GraphML: از ساختار تگ XML برای ذخیره‌سازی اطلاعات پیرامون گراف‌ها استفاده می‌کند و پسوند آن graphml. است. در اینجا، تگ graphml «فراداده»‌هایی (metadata) پیرامون گراف، تگ graph ویژگی‌هایی در رابطه با گراف، تگ nodes همه مشخصات مربوط به گره‌ها و در نهایت تگ edge مشخصه‌های یال‌ها را تعیین می‌کند. همچنین، یک تگ کلیدی اختیاری نیز وجود دارد که می‌توان از آن برای تخصیص وزن به یال‌ها و ویژگی به گره‌ها استفاده کرد.

۵. فرمت GEXF :GEXF سرنامی برای عبارت «Graph Exchange XML» و توسعه داده شده توسط سازمان Gephi است. این فرمت شباهت زیادی به فرمت graphXML دارد. GEXF زبانی برای توصیف ساختارهای شبکه پیچیده، داده‌های اختصاص یافته به آن‌ها و دینامیک‌های شبکه محسوب می‌شود. ابزار Gelphi همچنین برای بصری‌سازی آسان گراف‌های شبکه مورد استفاده قرار می‌گیرد.

مجموعه داده‌های بالا را می‌توان از مخازنی مانند SNAP ،(+) Konect ،(+) UCI (+) و دیگر وب‌سایت‌هایی که به ارائه مجموعه داده‌های عمومی می‌پردازند دانلود کرد. برای تحلیل این مجموعه داده‌ها، استفاده از کتابخانه‌های محبوب پایتون شامل networkx و MatplotLib گزینه بسیار خوبی محسوب می‌شود. در ادامه، برای شروع یک مثال ارائه شده است.

1# Draws circular plot of the network
2import matplotlib.pyplot as plt
3import networkx as nx
4
5G = nx.karate_club_graph() # data can be read from above specified formats. Refer documentation
6print("Node Degree")
7for v in G:
8    print (v, G.degree(v))
9nx.draw_circular(G, with_labels=True)
10plt.show()

استفاده از کتابخانه NetworkX

مثالی را در نظر بگیرید که طی آن، در یک باشگاه کاراته معروف که با عنوان Zachary karate club شناخته شده، دو استاد دارای کشمکش هستند و سعی دارند اعضای گروه دیگری را جذب کنند. آشکار است که در پایان این جدال دو گروه باقی خواهند ماند. آیا می‌توان با توجه به مشخصه‌های گراف پیش‌بینی کرد آن گروه‌ها چه هستند و چه کسی سمت کدام استاد را گرفته است؟

فیلم آموزش گراف کاوی و تحلیل شبکه ها در پایتون با NetworkX در فرادرس

کلیک کنید

نکته قابل توجه در این وهله آن است که یال‌های میان جامعه‌ای دارای «میانی» (betweenness) بالایی هستند. منظور از میانی تعداد کوتاه‌ترین مسیرها بین دو گره است. این‌ها یال‌هایی هستند که گراف را متصل نگه داشته و در نقش پل عمل می‌کنند. کاری که می‌توان انجام داد آن است که این یال‌ها تا حد امنی حذف شوند و جوامع باقی‌مانده از جهت غیر متصل بودن در آن نقطه مورد بررسی قرار بگیرند.

1import networkx as nx  # Python 2.x, NetworkX 2.0
2import networkx as nx
3def edge_to_remove(G):  # high betweenness edges are removed first
4 dic1 = nx.edge_betweenness_centrality(G)
5 list_tuples = dic1.items()
6 list_tuples.sort(key =lambda x:x[1], reverse = True)
7 return list_tuples[0][0] #(a,b)
8def girvan(G): # returns number of connected components
9 c = nx.connected_component_subgraphs(G)
10 i=0
11 while(i<11): # you can experiment with different values
12  G.remove_edge(*edge_to_remove(G)) 
13 return c
14G = nx.karate_club_graph() # imports popular zachary karate club
15c = girvan(G) # After enough edge removal, groups printed
16for i in c:
17 print 'Group Nodes: ', i.nodes()
18 print 'Number Of Nodes: ', i.number_of_nodes()
19Output :
20Group Nodes:  [0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21]
21Number Of Nodes:  15
22Group Nodes:  [32, 33, 2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]
23Number Of Nodes:  19

اکنون، ویژگی اتصال (connectedness) همراه با جزئیات بیشتر و اطلاعات جالبی که با اعمال ساختارهای اجتماعی بر آن قابل اشتقاق است مورد بررسی قرار می‌گیرد. از چه اطلاعات بیشتری می‌توان پرده‌برداری کرد؟ مثالی مفروض است که در آن شخصی اهل دهلی (Daman) قصد داشت در سال ۱۹۷۰ با یک سرویس پست یا ایمیل به Lana در لوس آنجلس متصل شود.

فیلم آموزش تجزیه و تحلیل و آماده سازی داده ها با پایتون Python در فرادرس

کلیک کنید

اکنون، منصفانه است که فرض شود همه جوامع در زمان خودشان متصل بوده‌اند، اما آیا گراف آشنایی جهان متصل است؟ برپایه استدلالی که در بالا اشاره شد، منصفانه است که گفته شود جهان متصل به حساب می‌آید. پرسش دیگر آن است که به منظور انتقال پیام به طور میانگین چند رابطه مورد نیاز است؟ پاسخ‌گویی به این سوال با استفاده از نظریه «شش درجه جدایی» (Six Degrees of Separation) امکان‌پذیر خواهد بود.

شش درجه جدایی

در پاسخ به پرسش بالا باید گفت، به طور میانگین تنها شش رابطه برای انتقال چنین پیامی مورد نیاز محسوب می‌شود. اما چرا تعداد رابطه‌ها انقدر کم است؟ پاسخ این پرسش «هموفیلی» (homophily) (گره‌های مشابه متصل می‌شوند و جوامعی را با ضریب همبستگی بالا شکل می‌دهند) و «روابط ضعیف» (Weak Ties) است.

فیلم آموزش تحلیل شبکه های اجتماعی با زبان R و متن کاوی Text Mining در فرادرس

کلیک کنید

هر دو این موارد در مثال Zachary club که در بالا مطرح شد، با دو جامعه حاصل شده به دلیل هموفیلی دو گره مشابه که متصل می‌شوند و یال‌های دارای میانی بالا و روابط ضعیفی که در آن دوستان یک فرد حتی ممکن است در گروه رقیب باشند تشریح شد.

در شبکه‌های جهان واقعی، این مساله با یک توصیف تصادفی قابل درک است که بر مبنای آن احتمال کمتری برای شکل دادن روابط طولانی در مقایسه با روابط کوتاه وجود دارد. دلیل این امر می‌تواند جغرافیایی باشد، مانند مساله بالا که منجر به داشتن هم‌پوشانی همسایگی کمتری شده است.

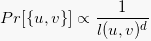
چگونه می‌توان این مساله را در مجموعه داده یک شبکه تشخیص داد؟ تنها کافی است طول میانگین کوتاه‌ترین مسیری که به ۶ نزدیک‌تر و یا به شدت در مقایسه با اندازه شبکه کوچک است تحلیل شود. این بدین معنا است که گراف/شبکه پدیده «جهان کوچک» (small world) را از خود نشان می‌دهد.

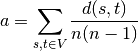
ابتدا گراف مورد نظر (هر گراف دلخواهی) در هر فرمتی که کاربر با آن راحت است باید از ورودی خوانده شود. سپس، تابع زیر قابل اعمال روی آن است.

1# Networkx Examples
2G =nx.karate_club_graph() # Can be applied on different graphs
3print(nx.average_shortest_path_length(G))
4G = nx.florentine_families_graph()
5print(nx.average_shortest_path_length(G))
6G = nx.davis_southern_women_graph()
7print(nx.average_shortest_path_length(G))

اکنون زمان آن رسیده که این کد روی مجموعه داده‌های جهان واقعی اعمال شود. در اینجا یک مجموعه داده فیس‌بوک که با SNAP ترکیب شده مورد استفاده قرار گرفته که شامل داده‌هایی از همه ego-net‌ها در قالب edgelist است. در ادامه سعی بر آن است که بررسی موردی انجام شده توسط کمبریج آنالیتیکا شبیه‌سازی شود، چگونگی اتصال کاربران به یکدیگر مورد بررسی قرار بگیرد و در نهایت خروجی حاصل با استفاده از کتابخانه matplotlib بصری‌سازی شود.

1G = nx.read_edgelist('Desktop/facebook_combined.txt')
2print(nx.average_shortest_path_length(G)) # Takes 4 mins approx.
3[Output]: 3.6925068497 # Confirms our statement above.

مساله مهم دیگری که در این وهله مطرح می‌شود آن است که تفسیر این نتایج چگونه انجام می‌شود؟ نتیجه حاصل یک گراف بسیار بزرگ با ویژگی میانگین کوتاه‌ترین مسیر بسیار کوچک است. این یعنی روابط بین هر دو گره‌ای در زمان ثابت (O(k قابل محاسبه است. مساله عنوان شده با عنوان «جست‌و‌جوی غیر متمرکز» (Decentralized Search) نیز شناخته شده است.

نتیجه‌گیری

تحلیل شبکه‌های اجتماعی بزرگ جهان واقعی با توجه به ویژگی‌های این شبکه‌ها (و با بهره‌گیری از قابلیت‌های داده‌کاوی) مزایای متعددی را به دنبال دارد و پژوهشگران با آگاهی از این ویژگی‌ها و مزایا به این حوزه گرایش قابل توجهی پیدا کرده‌اند.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

علاوه بر اتصال، ویژگی‌های مهم دیگری نیز برای اکتشاف در شبکه‌های اجتماعی وجود دارد که از آن جمله می‌توان به Power Law، «اثر آبشاری» (Cascading Effect)، «پیش‌بینی لینک» (Link Prediction)، سازمان‌دهی فضایی و اجتماعی، Pseudo core‌ها و شبکه‌های تکاملی اشاره کرد که هر یک نیازمند بحث تخصصی خود هستند. داشتن دانش پیرامون این مباحث به ساده‌سازی مسائل تحلیل شبکه و کاهش زمان و تلاش مورد نیاز برای تحلیل مجموعه داده‌های بزرگ کمک قابل توجهی می‌کند.

اگر نوشته بالا برای شما مفید بود، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آموزش تحلیل شبکه‌های اجتماعی با نرم افزار نود ایکس ال (NodeXL)
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های هوش محاسباتی
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های شبکه‌های عصبی مصنوعی
• گنجینه آموزش‌های برنامه نویسی پایتون (Python)

^^