شبکههای عصبی در پایتون و R – درک و کد نویسی از صفر تا صد

هر مفهومی را به دو روش میتوان یاد گرفت و عملی کرد.
- روش اول: میتوان کل مباحث نظری را در خصوص یک موضوع خاص آموخت و سپس به دنبال روشهایی برای استفاده از آن مفاهیم گشت. در این روش شما در مورد چگونگی عملکرد کلی الگوریتم مطالعه میکنید، ریاضیات مبنای آن را درک میکنید، فرضیات و محدودیتهای آن را میشناسید و سپس از آن استفاده میکنید. این روش، یک رویکرد خوب ولی زمانبر است.
- روش دوم: کار خود را با مطالعه مفاهیم اولیه آغاز میکنید و به یک شهود کلی از موضوع دست مییابید. سپس یک مسئله را انتخاب کرده و شروع به حل آن میکنید. در حین حل مسئله بیشتر با مفاهیم مرتبط آشنا میشوید. بدین ترتیب فرآیند آموزش و بهبود درک، ادامه مییابد. به طور خلاصه در این روش شما ابتدا راههای بهکارگیری الگوریتم را مطالعه میکنید و سپس آن را عملاً اجرا میکنید. زمانی که روش استفاده از آن را یاد گرفتید، پارامترها، مقادیر و محدودیتهای مختلف آن را میآزمایید و بدین ترتیب به درکی از نحوه عملکرد الگوریتم دست مییابید.
روش دوم برای یادگیری موضوعات جدید رویکرد بهتری محسوب میشود. شاید درک ریاضیات مبنای تشکیلدهنده یک الگوریتم کار دشواری باشد، اما رسیدن به یک شهود کلی در مورد آن کار آسانی است. میتوان بر اساس آزمایشها و ادراکات قبلی بهترین سناریوها را برای بهکارگیری یک الگوریتم مشخص کرد.
معمولاً افراد برای رسیدن به این شهود کلی که در مورد آن صحبت کردیم، وقت نمیگذارند و بدین ترتیب برای بهکارگیری صحیح الگوریتمها دچار مشکل میشوند.
در این نوشته به بررسی بلوکهای سازندهی یک شبکه عصبی از پایه میپردازیم و بر روی رسیدن به یک شهود کلی برای بهکارگیری شبکههای عصبی تأکید داریم. ما هم در زبان پایتون و هم در R کد نویسی خواهیم کرد. در انتهای این نوشته شما در مورد نحوه عملکرد شبکههای عصبی، نحوه مقداردهی اولیه وزنها و چگونگی بهروزرسانی آنها با استفاده از روش پس-انتشار (back-propagation) خواهید آموخت.
شهود ساده مبنای عمل شبکههای عصبی
اگر یک توسعهدهنده نرمافزار باشید یا دستکم با فرایند توسعه کد آشنایی داشته باشید، میدانید که چگونه باید در یک کد به دنبال باگها بگردید. میبایست موارد تست مختلفی را با تغییر دادن ورودیها، اجرا کنید و خروجیها را بررسی کنید. ایراداتی که در خروجی رخ میدهند، سرنخی محسوب میشوند که کجا باید به دنبال باگ بگردیم، و کدام ماژول را بررسی و کدام خطهای کد را مطالعه کنیم. زمانی که باگها را شناسایی کردیم، تغییرات لازم را در کد ایجاد میکنیم و به این فرایند ادامه میدهیم تا زمانی که به کد/برنامه مناسب برسیم.
الگوریتم شبکههای عصبی نیز به روش کاملاً مشابهی عمل میکند. این الگوریتم چند ورودی میگیرد، با استفاده از نورونها در چند لایه پنهان آنها را پردازش میکند و با استفاده از یک لایه خروجی نتیجه را بازمیگرداند. این فرآیند تخمین نتیجه، از نظر فنی «پیش-انتشار» (Forward Propagation) نامیده میشود.
سپس نتیجه را با خروجی واقعی مقایسه میکنیم. هدف این است که خروجی شبکه عصبی را تا حد امکان به خروجی واقعی (مطلوب) نزدیک کنیم. هریک از نورونها در مقداری از خطای خروجی نهایی مشارکت میکنند. چگونه میتوان این خطا را کاهش داد؟
روش کار این است که سعی میکنیم ارزش/وزن نورونهایی که در خطا مشارکت دارند را کاهش دهیم. برای انجام این کار به عقب برمیگردیم و نورونهایی را مییابیم که در شبکه عصبی خطا ایجاد میکنند. این فرآیند به نام «پس-انتشار» (Back Propagation) شناخته میشود.
برای کاهش دفعات این تکرارها جهت کمینهسازی خطا، شبکههای عصبی از الگوریتمهای رایجی به نام «گرادیان کاهشی» (Gradient Descent) استفاده میکنند که به بهبود سرعت و کارآمدی الگوریتم کمک میکند.
توضیحات بالا کل فرایند کاری شبکههای عصبی را توضیح میدهد. گرچه این یک بازنمایی ساده محسوب میشود، اما کمک میکند مسائل را به روش سادهای درک کنیم.
پرسپترون چند لایه و مفاهیم آن
همانطور که اتمها، اساس تشکیلدهنده هر مادهای بر روی زمین هستند، واحدهای تشکیلدهنده پایهای شبکه عصبی نیز پرسپترون نام دارند. به عنوان مثال به تصویر زیر نگاه کنید.
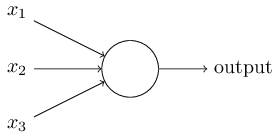
ساختار فوق سه ورودی دارد و یک خروجی تولید میکند. سؤال منطقی که اینجا پیش میآید، این است که رابطه بین ورودی و خروجی چیست؟ ابتدا حالتهای ساده آن را توضیح میدهیم و سپس روشهای پیچیدهتر را بررسی میکنیم.
در ادامه سه روش ایجاد رابطه بین ورودی و خروجی را توضیح دادهایم.
1. ترکیب مستقیم ورودی و محاسبه خروجی بر اساس یک مقدار آستانه
برای مثال فرض کنید x1=0، x2=1، x3=1 و مقدار آستانه نیز برابر با صفر تعیین شده است. در این صورت اگر x1+x2+x3>0، مقدار خروجی 1 و در غیر این صورت 0 است. میبینیم که در این حالت، پرسپترون مقدار خروجی برابر با 1 محاسبه میکند.
2. در این مرحله به ورودیها وزن میدهیم
وزنها باعث میشوند که یک ورودی اهمیت پیدا کند. برای مثال برای ورودیهای x2، x1 و x3 به ترتیب وزنهای w2=3، w1=2 و w3=4 تعیین میکنیم. برای محاسبه خروجی، ورودیها را در وزنهای مربوطه ضرب کرده و با مقدار آستانه به صورت زیر مقایسه میکنیم.
w1*x1 + w2*x2 + w3*x3 >آستانه
این وزنها باعث میشوند که ورودی x3 در مقایسه با x1 و x2 اهمیت بیشتری پیدا کند.
3. در این مرحله بایاس (bias) را اضافه میکنیم
هر پرسپترون درون خود یک مقدار بایاس نیز دارد که میتوان آن را به عنوان شاخص انعطافپذیری پرسپترون در نظر گرفت. این مفهوم تا حدود زیادی شبیه مقدار ثابت b در یک تابع خطی به صورت y = ax + b است. این مقدار به ما کمک میکند که خط خودمان را بالا و پایین ببریم تا بهتر با پیشبینی دادهها منطبق شود. اگر این مقدار b وجود نداشته باشد، همیشه باید از مبدأ مختصات (0,0) کار خود را آغاز کنیم و بدین ترتیب مطابقت ضعیفی خواهیم داشت. برای مثال یک پرسپترون میتواند ۲ ورودی داشته باشد که در این حالت نیازمند 3 وزن است. هر یک از ورودیهای یک وزن دارند و یک وزن نیز به بایاس داده میشود. اینک نمایش خطی ورودی چیزی شبیه زیر خواهد بود:
w1*x1 + w2*x2 + w3*x3 + 1*b
اما با وجود همه این اصلاحات هنوز هم معادله ما که روش کار پرسپترون را نشان میدهد، یک معادله خطی است. اما این حالت چندان جالب نیست. بنابراین افراد مختلف تلاش کردهاند تا یک پرسپترون ایجاد کنند که امروزه آن را نورون مصنوعی مینامیم. این نورون از تبدیلهای غیرخطی (تابع فعالسازی) در مورد ورودیها و بایاسها استفاده میکند.
تابع فعالسازی (activation function) چیست؟
این تابع مجموعه ورودیهای وزندار ((w1*x1 + w2*x2 + w3*x3 + 1*b)) را به عنوان یک آرگومان دریافت میکند و خروجی نورون را بازمیگرداند:
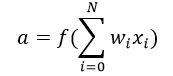
در معادله فوق 1 را به عنوان x0 و b را به عنوان w0 در نظر گرفتیم. تابع فعالسازی به طور عمده برای ایجاد تبدیلهای غیرخطی استفاده میشود. این تبدیلها امکان مطابقت با فرضیات غیرخطی و یا تخمین تابعهای پیچیده را فراهم میسازند. چند تابع فعالسازی وجود دارند مانند توابع «Sigmoid»، «Tanh» ،«ReLu» و موارد دیگر.
پیش-انتشار، پس-انتشار و تکرارها
تا به اینجا، خروجی را محاسبه کردیم که این فرایند به نام پیش-انتشار نامیده میشود. اما اگر خروجی تخمین زده شده، از خروجی واقعی بسیار دور باشد (خطای بالا) چه میتوان کرد؟ در شبکههای عصبی برای حل این مسئله بایاسها و وزنهای نورونهای خطادار بهروزرسانی میشوند. این بهروزرسانی وزن و بایاس به نام پس-انتشار نامیده میشود.
الگوریتمهای پس-انتشار (BP) با تعیین زیان (یا خطا) در خروجی و سپس بازگرداندن آن به شبکه عمل میکنند. وزنها طوری بهروزرسانی میشوند که خطای حاصل از هر نورون به کمترین مقدار برسد. گام نخست کمینهسازی خطا، تعیین گرادیان (مشتق) هر گره نسبت به خروجی نهایی است. برای داشتن یک دید ریاضی از الگوریتم پس-انتشار به بخشهای بعدی مراجعه کنید.
این حلقه پیش-انتشار و پس-انتشار به عنوان تکرار آموزش یا «Epoch» نامیده میشود.
پرسپترون چند لایه
اینک میخواهیم بخش بعدی که پرسپترون چند لایه است را توضیح بدهید. تاکنون ما تنها یک لایه منفرد را که شامل سه گره ورودی مانند x2، x1 و x3 و یک لایه خروجی که شامل یک نورون منفرد بود را ملاحظه کردیم. اما در استفادههای عملی، شبکه تک لایه کاربرد چندانی ندارد. پرسپترون چند لایه (MLP) شامل چندین لایه است که به نام لایههای پنهان نامیده میشوند و مطابق شکل زیر بین لایههای ورودی و لایههای خروجی پشته سازی شدهاند.
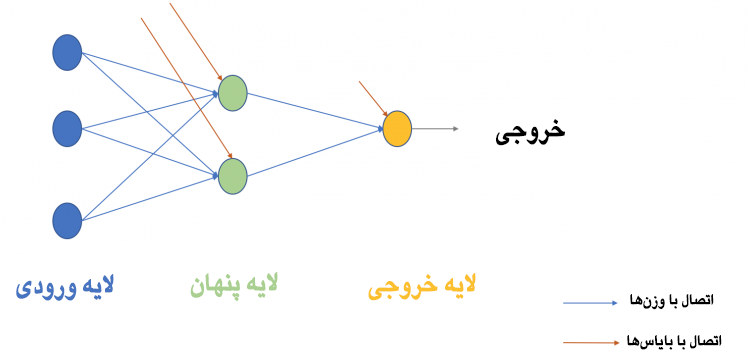
تصویر فوق تنها یک لایه پنهان منفرد را به رنگ سبز نشان میدهد، اما در عمل میتوانیم چندین لایه پنهان داشته باشیم. مورد دیگری که باید مورد اشاره قرار گیرد، این است که همه لایهها کاملاً به هم متصل هستند. یعنی در هر لایه (به جز لایه ورودی و خروجی) همه گرهها به همه گرههای لایه قبلی و لایه بعدی متصل میشوند.
در بخش بعدی، الگوریتمهای تمرینی برای یک شبکه عصبی (جهت کاهش خطا) بررسی شدهاند. در این بخش به الگوریتمهای تمرینی رایج که به نام گرادیان کاهشی مشهورند، میپردازیم.
گرادیان کاهشی دسته کامل و گرادیان کاهشی تصادفی
هر دو نسخه گرادیان کاهشی کار مشابه بهروزرسانی وزنهای MLP را از طریق الگوریتم بهروزرسانی مشابهی انجام میدهند. اما اختلاف آن دو در تعداد نمونههای تمرینی مورداستفاده برای بهروزرسانی وزنها و بایاسها است.
الگوریتم گرادیان کاهشی دسته کامل، همانطور که از نامش مشخص است از همه نقاط دادهای تمرینی برای بهروزرسانی هریک از وزنها استفاده میکند، در حالی که گرادیان تصادفی از یک یا چند نمونه استفاده میکند، اما هرگز از کل دادههای تمرینی برای بهروزرسانی وزنها به صورت یکباره استفاده نمیکند.
با یک مثال ساده از مجموعه 10 نقطه دادهای با دو وزن w1 و w2 موضوع را روشنتر میکنیم.
گرادیان کاهشی دسته کامل: در این روش از ۱۰ نقطه دادهای (کل داده تمرینی) استفاده کرده و تغییرات در w1 (Δw1) و تغییرات در w2 (Δw2) را محاسبه کرده و آن دو را بهروزرسانی میکنیم.
گرادیان کاهشی تصادفی (SGD): در این روش ابتدا با استفاده از یک نقطه دادهای، تغییرات در w1 (Δw1) و تغییرات در w2 (Δw2) محاسبه شده و آن دو نقطه بهروزرسانی میشوند. سپس با استفاده از نقطه دادهای دوم، وزنها را بهروزرسانی میکنیم.
مراحل مختلف روششناسی شبکه عصبی
در ادامه به روش ساخت گامبهگام روششناسی شبکه عصبی (MLP) با یک لایهی پنهان خواهیم پرداخت. در لایه خروجی ما تنها یک نورون داریم، چون در حال حل کردن یک مسئله طبقهبندی دودویی (پیشبینی 0 یا 1 هستیم). همچنین میتوانستیم برای پیشبینی هر یک از این دو کلاس 2 نورون داشته باشیم.
مراحل کلی کار به صورت زیر است.
بخش پیش-انتشار
0. ورودی و خروجی را مشخص میکنیم
- X به عنوان یک ماتریس ورودی
- y به عنوان یک ماتریس خروجی
1. مقادیر اولیه وزنها و بایاسها را به صورت تصادفی تعیین میکنیم (این فرایند اولیه یکبار رخ میدهد و در تکرارهای بعدی از وزنها و بایاسهای بهروز شده استفاده میکنیم).
- wh به عنوان ماتریس وزن برای لایه پنهان
- bh به عنوان ماتریس بایاس برای لایه پنهان
- wout به عنوان ماتریس وزن برای لایه خروجی
- bout به عنوان ماتریس بایاس برای لایه خروجی
2. ابتدا حافظه داخلی ماتریس ورودی و وزنهای دادهشده به یالهای بین لایه ورودی و لایه پنهان را محاسبه کردیم و سپس بایاسهای نورونهای لایه پنهان را به ورودیهای مربوطه اضافه میکنیم. این فرآیند به نام تبدیل خطی مشهور است:
Hidden_layer_input= matrix_dot_product(X,wh) + bh
3. تبدیل غیرخطی با استفاده از یک تابع فعالسازی سیگموئید (Sigmoid) انجام مییابد. تابع سیگموئید خروجی را به صورت 1/(1 + exp(-x)) بازمیگردند.
Hiddenlayer_activations = sigmoid(hidden_layer_input)
4. تبدیل خطی بر روی فعالسازی لایه پنهان انجام میشود (حاصلضرب داخلی ماتریس با وزن محاسبه شده و نورون لایه خروجی اضافه میشود) سپس یک تابع فعالسازی بر روی آن استفاده میشود (در این حالت نیز از تابع سیگموئید استفاده میشود) اما میتوان بسته به نوع کاری که انجام میدهیم، از توابع فعالسازی دیگری نیز استفاده نمود) و به این ترتیب خروجی پیشبینی میشود.
Output_layer_input = matrix_dot_product (hiddenlayer_activations * wout) + bout
output = sigmoid(output_layer_input)
همه گامهایی که در بالا اشاره کردیم به نام روش پیش-انتشار (Forward Propagation) نامیده میشود.
بخش پس-انتشار
5. سپس مقادیر پیشبینی شده با خروجی واقعی مقایسه شده و گرادیان خطا (مقدار واقعی منهای مقدار پیشبینی شده) محاسبه میشود. در اینجا خطا به معنی مربع زیان است ((Y-t)^2)/2
E = y – output
6. شیب/گرادیان نورونهای لایه پنهان و خروجی محاسبه میشود (برای محاسبه شیب، نخست مشتقهای فعالسازی غیرخطی x در هر لایه برای هر نورون محاسبه میشود) گرادیان سیگموئید معمولاً به صورت * (1 – x) بازگردان میشود.
Slope_output_layer = derivatives_sigmoid(output)
slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
7. مقدار تغییر (دلتا) در لایه خروجی، بسته به گرادیان خطا ضرب در شیب فعالسازی لایه خروجی محاسبه میشود
D_output = E * slope_output_layer
8. در این مرحله خطا به شبکه بازگردان میشود و این بدان معنی است که خطا به لایه پنهان داده میشود. به این منظور حاصلضرب داخلی دلتای لایه خروجی همراه با پارامترهای وزنی یالهای بین لایه پنهان و خروجی محاسبه میشود (wout.T)
Error_at_hidden_layer = matrix_dot_product(d_output, wout.Transpose)
9. مقدار تغییرات (دلتا) در لایه پنهان محاسبه شده، مقدار خطا در لایه پنهان با شیب فعالسازی لایه پنهان ضرب میشود
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
10. وزنها در لایه خروجی و پنهان بهروزرسانی میشوند. وزنها در این شبکه از طریق خطاهای محاسبه شده برای نمونههای تمرینی میتوانند بهروزرسانی شوند
Wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate
wh = wh + matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_rate
نرخ یادگیری: مقدار بهروزرسانی وزنها از طریق یک پارامتر پیکربندی به نام نرخ یادگیری کنترل میشود.
11. بایاسها در لایه پنهان و لایه خروجی بهروزرسانی میشوند. بایاسهای موجود در شبکه را میتوان از طریق خطاهای تجمیع شده در آن نورون بهروزرسانی کرد.
- bias at output_layer =bias at output_layer + sum of delta of output_layer at row-wise * learning_rate
- bias at hidden_layer =bias at hidden_layer + sum of delta of output_layer at row-wise * learning_rate
bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate
bout = bout + sum(d_output, axis=0)*learning_rate
مراحل ۵ تا ۱۱ به نام روش «پس-انتشار» (Backward Propagation) نامیده میشوند.
هر بار تکرار پس-انتشار و پیش-انتشار به صورت یک چرخه تمرین در نظر گرفته میشود. همانطور که قبلاً اشاره کردیم زمانی که بار دوم به تمرین دادن اقدام میکنیم، بهروزرسانی وزنها و بایاسها برای پیش-انتشار استفاده میشود.
تا اینجا ما وزنها و بایاسهای لایه خروجی و پنهان را بهروزرسانی کردیم و از الگوریتم گرادیان کاهشی دستهی کامل استفاده کردیم.

تصویرسازی مراحل روششناسی شبکه عصبی
مراحلی که در بخش بالا معرفی کردیم را تکرار میکنیم تا ورودی، وزنها، بایاسها، خروجی، ماتریس خطا را به تصویر بکشیم و روششناسی عملی شبکه عصبی (MLP) را درک کنیم.
توجه:
- برای تصویرسازی بهتر مقادیر اعشاری تا 2 یا 3 رقم اعشار گرد شدهاند.
- سلولهایی که به رنگ زرد درآمدهاند، نشاندهنده سلولهای فعال کنونی هستند.
- سلولهای نارنجی نشاندهنده ورودی مورداستفاده برای رسیدن به مقادیر سلول کنونی هستند.
گام 0: خواندن ورودی و خروجی

گام ۱: وزنها و بایاسها با مقادیر تصادفی، مقداردهی اولیه میشوند (روشهایی برای مقداردهی اولیه وزنها و بایاسها وجود دارند، اما در این مرحله از روش مقادیر تصادفی استفاده میکنیم)

گام 2: محاسبه ورودی لایه پنهان:
Hidden_layer_input= matrix_dot_product(X,wh) + bh

گام 3: اجرای تبدیل غیرخطی بر روی ورودی لایه پنهان
hiddenlayer_activations = sigmoid(hidden_layer_input)

گام ۴: اجرای تبدیل خطی و غیرخطی فعالسازی لایه پنهان در ناحیه خارجی
Output_layer_input = matrix_dot_product (hiddenlayer_activations * wout) + bout
output = sigmoid(output_layer_input)

گام ۵: محاسبه گرادیان خطا (E) در لایه خروجی
E = y-output

گام ۶: محاسبه شیب در لایه خروجی و لایه پنهان
Slope_output_layer= derivatives_sigmoid(output)
Slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
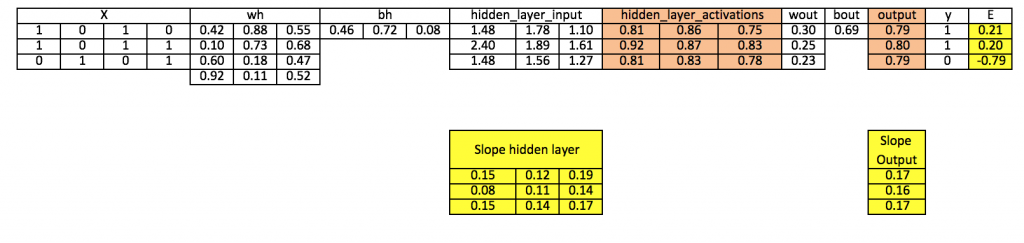
گام 7: محاسبه دلتا در لایه خروجی
d_output = E * slope_output_layer*lr
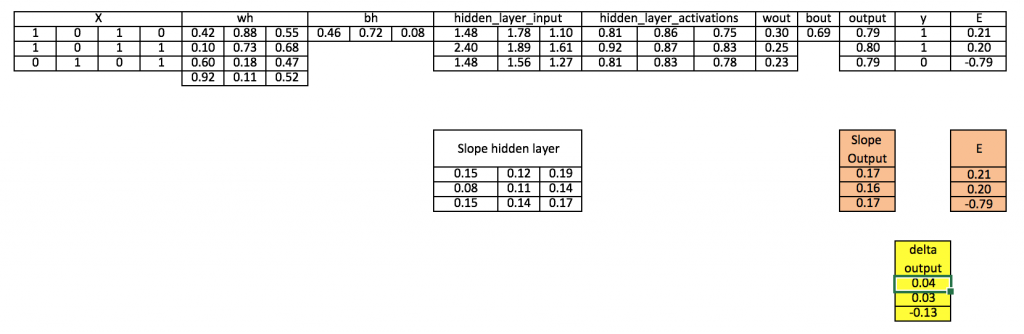
گام ۸: محاسبه خطا در لایه پنهان
Error_at_hidden_layer = matrix_dot_product(d_output, wout.Transpose)
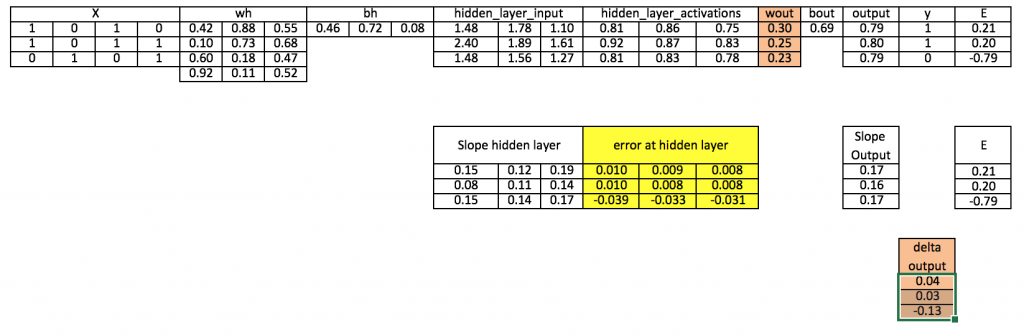
گام 9: محاسبه دلتا در لایه پنهان
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
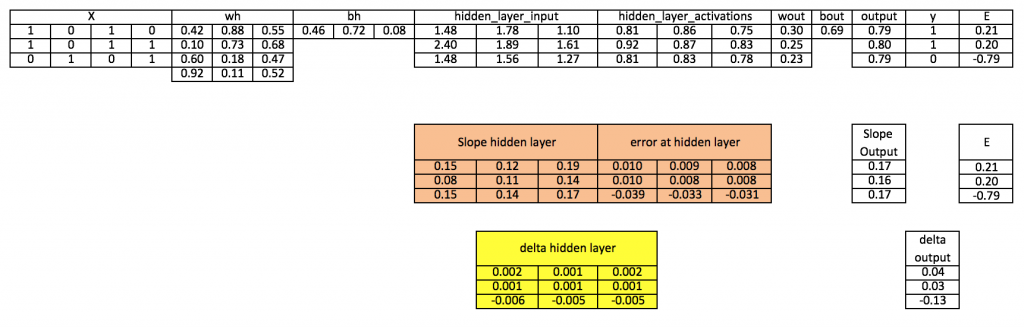
گام 10: بهروزرسانی وزن در هر دو لایه پنهان و خروجی
Wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate
wh = wh+ matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_rate
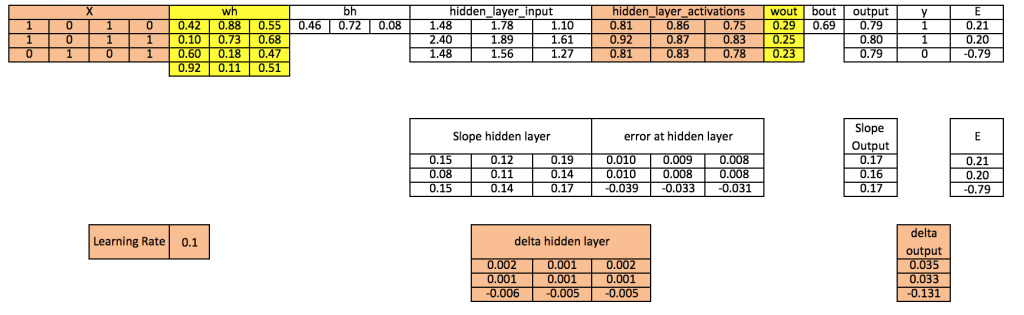
گام ۱۱: بهروزرسانی بایاسها در هر دو لایه پنهان و خروجی
bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate
bout = bout + sum(d_output, axis=0)*learning_rate
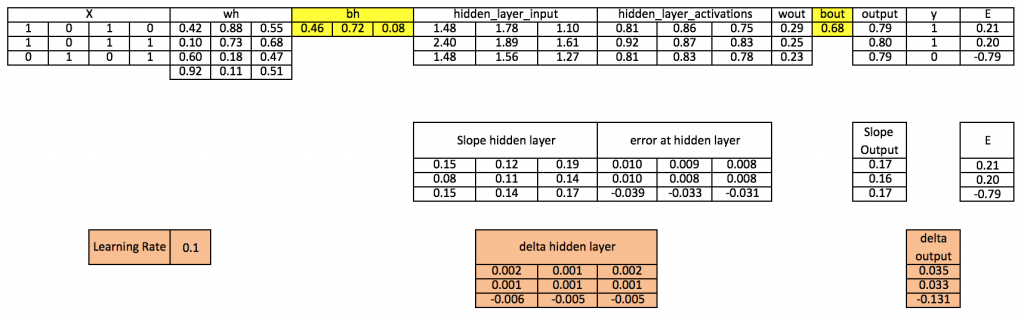
به این ترتیب میبینیم که هنوز خطای زیادی وجود دارد و نتوانستیم به مقدار هدف واقعی نزدیک شویم، زیرا تنها یک چرخه تکرار تمرین را به پایان بردهایم. اگر مدل خود را چند بار تمرین بدهیم، در این صورت به خروجی واقعی بسیار نزدیک خواهیم شد. ما در این مثال هزاران تکرار را اجرا کردیم و نتیجهای که به دست آوردیم، بسیار به مقدار هدف واقعی نزدیک است:
([[0.98032096] [0.96845624] [0.04532167]]).
پیادهسازی شبکه عصبی (NN) با استفاده از Numpy (Python)
import numpy as np #Input array X=np.Array([[1,0,1,0], [1,0,1,1], [0,1,0,1]]) #Output y=np.Array([[1], [1], [0]]) #Sigmoid Function def sigmoid (x): return 1/(1 + np.Exp(-x)) #Derivative of Sigmoid Function def derivatives_sigmoid(x): return x * (1-x) #Variable initialization epoch=5000 #Setting training iterations lr=0.1 #Setting learning rate inputlayer_neurons = X.Shape[1] #number of features in data set hiddenlayer_neurons = 3 #number of hidden layers neurons output_neurons = 1 #number of neurons at output layer #weight and bias initialization wh=np.Random.Uniform(size=(inputlayer_neurons,hiddenlayer_neurons)) bh=np.Random.Uniform(size=(1,hiddenlayer_neurons)) wout=np.Random.Uniform(size=(hiddenlayer_neurons,output_neurons)) bout=np.Random.Uniform(size=(1,output_neurons)) for i in range(epoch): #Forward Propogation hidden_layer_input1=np.Dot(X,wh) hidden_layer_input=hidden_layer_input1 + bh hiddenlayer_activations = sigmoid(hidden_layer_input) output_layer_input1=np.Dot(hiddenlayer_activations,wout) output_layer_input= output_layer_input1+ bout output = sigmoid(output_layer_input) #Backpropagation E = y-output slope_output_layer = derivatives_sigmoid(output) slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations) d_output = E * slope_output_layer Error_at_hidden_layer = d_output.Dot(wout.T) d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer wout += hiddenlayer_activations.T.Dot(d_output) *lr bout += np.Sum(d_output, axis=0,keepdims=True) *lr wh += X.T.Dot(d_hiddenlayer) *lr bh += np.Sum(d_hiddenlayer, axis=0,keepdims=True) *lr print output
پیادهسازی شبکه عصبی در R
# input matrix
X=matrix(c(1,0,1,0,1,0,1,1,0,1,0,1),nrow = 3, ncol=4,byrow = TRUE)
# output matrix
Y=matrix(c(1,1,0),byrow=FALSE)
#sigmoid function
sigmoid<-function(x){
1/(1+exp(-x))
}
# derivative of sigmoid function
derivatives_sigmoid<-function(x){
x*(1-x)
}
# variable initialization
epoch=5000
lr=0.1
inputlayer_neurons=ncol(X)
hiddenlayer_neurons=3
output_neurons=1
#weight and bias initialization
wh=matrix(rnorm(inputlayer_neurons*hiddenlayer_neurons,mean=0,sd=1), inputlayer_neurons, hiddenlayer_neurons)
bias_in=runif(hiddenlayer_neurons)
bias_in_temp=rep(bias_in, nrow(X))
bh=matrix(bias_in_temp, nrow = nrow(X), byrow = FALSE)
wout=matrix(rnorm(hiddenlayer_neurons*output_neurons,mean=0,sd=1), hiddenlayer_neurons, output_neurons)
bias_out=runif(output_neurons)
bias_out_temp=rep(bias_out,nrow(X))
bout=matrix(bias_out_temp,nrow = nrow(X),byrow = FALSE)
# forward propagation
for(i in 1:epoch){
hidden_layer_input1= X%*%wh
hidden_layer_input=hidden_layer_input1+bh
hidden_layer_activations=sigmoid(hidden_layer_input)
output_layer_input1=hidden_layer_activations%*%wout
output_layer_input=output_layer_input1+bout
output= sigmoid(output_layer_input)
# Back Propagation
E=Y-output
slope_output_layer=derivatives_sigmoid(output)
slope_hidden_layer=derivatives_sigmoid(hidden_layer_activations)
d_output=E*slope_output_layer
Error_at_hidden_layer=d_output%*%t(wout)
d_hiddenlayer=Error_at_hidden_layer*slope_hidden_layer
wout= wout + (t(hidden_layer_activations)%*%d_output)*lr
bout= bout+rowSums(d_output)*lr
wh = wh +(t(X)%*%d_hiddenlayer)*lr
bh = bh + rowSums(d_hiddenlayer)*lr
}
output
چشمانداز ریاضیاتی الگوریتم پس-انتشار (برای مطالعه بیشتر)
فرض کنیم Wi وزنهای بین لایه ورودی و لایه پنهان باشد. همچنین Wh وزنهای بین لایه پنهان و لایه خروجی باشد.
حال h=σ (u)= σ (WiX) یعنی h تابعی از u است و u تابعی از Wi و X است. ما در اینجا تابعمان را به صورت σ نشان دادهایم
Y= σ (u’)= σ (Whh) یعنی Y تابعی از 'u است و 'u تابعی از Wh و h است.
ما به طور مداوم برای محاسبه مشتقات جزئی به معادلات فوق ارجاع خواهیم داد.
ما به طور مقدماتی به دنبال یافتن مقادیر زیر هستیم
∂E/∂Wi و ∂E/∂Wh
این دو مقدار نشاندهنده تغییر در خطا در زمان تغییر وزنها بین لایه ورودی و پنهان و همچنین تغییر در خطا در زمان تغییر یافتن وزنها بین لایه پنهان و لایه خروجی هستند.
اما برای محاسبه هر دوی این مشتقات جزئی میبایست از قاعده زنجیری دیفرانسیل جزئی استفاده کنیم زیرا E تابعی از Y است و Y تابعی از 'u است و خود 'u تابعی از Wi است.
به این ترتیب از خاصیت فوق استفاده کرده و گرادیانها را محاسبه میکنیم:
∂E/∂Wh = (∂E/∂Y). (∂Y/∂u’). (∂u’/∂Wh), …….. (1)
میدانیم که E به شکل E=(Y-t)2/2 است.
بنابراین
(∂E/∂Y)= (Y-t)
حال σ یک تابع سیگموئید است و یک دیفرانسیل مطلوب به شکل σ(1-σ) دارد. توصیه میکنیم خوانندگان خود به طور شخصی این رویه را بررسی کرده و صحت آن را تأیید کنند.
بنابراین
(∂Y/∂u’)= ∂(σ(u’)/∂u’= σ(u’)(1-σ(u’)).
اما σ(u’)=Y, بنابراین
(∂Y/∂u’)=Y(1-Y)
حال میدانیم که
(∂u’/∂Wh)= ∂(Whh)/∂Wh = h
با جایگزینی مقادیر در معادله (1) رابطه زیر به دست میآید:
∂E/∂Wh = (Y-t). Y(1-Y).h
پس اینک گرادیان بین لایه پنهان و لایه خروجی را محاسبه کردهایم. حال نوبت آن است که گرادیان بین لایه ورودی و لایه پنهان را محاسبه کنیم.
∂E/∂Wi =(∂ E/∂ h). (∂h/∂u). (∂u/∂Wi)
اما میدانیم که
(∂ E/∂ h) = (∂E/∂Y). (∂Y/∂u’). (∂u’/∂h)
با جایگزینی این مقدار در معادله بالا به معادله زیر دست مییابیم.
∂E/∂Wi =[(∂E/∂Y). (∂Y/∂u’). (∂u’/∂h)]. (∂h/∂u). (∂u/∂Wi) (2)
بنابراین در اینجا متوجه میشویم که چرا ابتدا گرادیان بین لایه پنهان و لایه خروجی را محاسبه کردیم.
همانطور که در معادله (2) دیده میشود ما قبلاً E/∂Y∂ و 'Y/∂u∂ را محاسبه کردهایم و در وقت و فضای خود صرفهجویی میکنیم. اینک نوبت آن است که بفهمیم چرا این الگوریتم، به نام الگوریتم پس-انتشار نامیده میشود.
∂u’/∂h = ∂(Whh)/∂h = Wh
∂h/∂u = ∂(σ(u)/∂u= σ(u)(1-σ(u))
اما
σ(u)=h
لذا
(∂Y/∂u)=h(1-h)
اینک
∂u/∂Wi = ∂(WiX)/∂Wi = X
با جایگزینی این مقادیر در معادله (2) به رابطه زیر دست مییابیم:
∂E/∂Wi = [(Y-t). Y(1-Y).Wi].h(1-h).X
بنابراین از آنجا که در حال حاضر هر دو گرادیان را محاسبه کردهایم، میتوانیم وزنها را به صورت زیر بهروزرسانی کنیم:
Wh = Wh + η. ∂E/∂Wh
Wi = Wi + η. ∂E/∂Wi
در روابط فوق η (اِتا) نشاندهنده نرخ یادگیری است.
بنابراین دوباره به این سؤال برمیگردیم که چرا این الگوریتم پس-انتشار نامیده شده است؟
دلیل آن این است که اگر به شکل نهایی E/∂Wh∂ و E/∂Wi∂ توجه کنید با عبارت (Y-t) مواجه میشوید یعنی خطای خروجی. این مقداری است که ما کار خود را با آن آغاز کردیم و سپس با حرکت به سمت عقب به لایه ورودی برای بهروزرسانی وزنها رسیدهایم.
به این ترتیب باید پرسید این منطق ریاضیاتی چگونه کد نویسی میشود؟
Hiddenlayer_activations=h
E= Y-t
Slope_output_layer = Y(1-Y)
Lr = η
Slope_hidden_layer = h(1-h)
Wout = Wh
اینک بهراحتی میتوانید کد را به آن ریاضیاتی که توضیح داده شد، مرتبط کنید.
سخن پایانی
در این نوشته بر روی بنای یک شبکه عصبی از صفر و درک مفاهیم مقدماتی آن تمرکز داشتیم. امیدواریم که اینک در مورد نحوه عمل یک شبکه عصبی به درک جامعی دست یافته باشید. حال میتوانید بفهمید که روشهای پس-انتشار و پیش-انتشار چگونه عمل میکنند، کارکرد الگوریتمهای بهینهسازی (گرادیان کاهشی دسته کامل و تصادفی) چیست، وزنها و بایاسها چگونه بهروزرسانی میشود و میتوانید هریک از مراحل را در نرمافزار Excel به تصویر بکشید و کد آن را در پایتون و R بنویسید.
در مقالات بعدی فرادرس به کاربرد استفاده از شبکه عصبی در پایتون و حل چالشهای واقعی در حوزههای زیر خواهیم پرداخت:
1. بینایی ماشین
2. تکلم
3. پردازش زبان طبیعی
خوشحالیم که در این نوشته با ما همراه بودید و از شما خواهش میکنیم هرگونه سؤال یا نظر و پیشنهادی که داشتید، در بخش نظرات با ما در میان بگذارید.
اگر به این نوشته علاقمند بوده اید، احتمالا مطالب زیر نیز برای شما مفید خواهند بود:
- مجموعه آموزش های شبکه های عصبی مصنوعی در متلب
- آموزش طبقه بندی و بازشناسی الگو با شبکه های عصبی LVQ در متلب
- آموزش نرمافزار نروسولوشن برای طراحی و پیادهسازی شبکه عصبی مصنوعی
==













سلام
توضیحات بسیار عالی و برای فهم عمومی مخاطب مبتدی مثل من با شیب بسیار ملایم شروع شد اما ناگهان میانه راه این شیب تند شد و فهم مطلب دشوار شد.
ممنون
درود
سپاس از شما برای ارائه بازخورد. برای درک بهتر «شبکههای عصبی» (Neural Networks) و مباحث مرتبط، مطالعه سه مطلب زیر به شما پیشنهاد میشود.
ساخت شبکه عصبی (Neural Network) در پایتون — به زبان ساده
شبکههای عصبی مصنوعی – از صفر تا صد
شاد و پیروز باشید.