کدگذاری گولومب – به زبان ساده

کدگذاری گولومب یک متد فشرده سازی داده بدون اتلاف است که از خانواده‌ای از کدهای فشرده‌سازی داده استفاده می‌کند که توسط سولومون گولومب در دهه 1960 ارائه شد. این کد از یک پارامتر تنظیم‌پذیر M برای تقسیم مقدار ورودی N به دو بخش q (نتیجه تقسیم بر M) و r (باقی مانده این تقسیم) استفاده می‌کند.

این روش کدگذاری برای شرایطی که رخداد مقادیر کوچک در جریان ورودی به صورت چشمگیری بیشتر از مقادیر بزرگ باشد مناسب است.

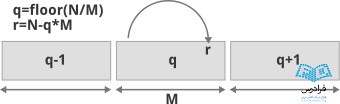
نحوه کدگذاری گولومب

یک کد گولومب، کدی با طول متغیر است. چیزی شبیه به کد هافمن، اما به جای اینکه مبتنی بر داده باشد (همچون هافمن) مبتنی بر مدلی ساده از احتمال مقادیر است (که صریحا به صورت اعداد طبیعی نمایش داده می‌شود به جای سمبل‌های انتزاعی): مقادیر کوچک احتمال رخداد بیشتری دارند تا مقادیر بزرگ. رابطه دقیق بین اندازه مقادیر و احتمال توسط یک پارامتر تعیین می‌شود، تقسیم کننده.

برای کدگذاری یک عدد (N) به روش گولومب، باید خارج قسمت (q) و باقی‌مانده (r) حاصل از تقسیم عدد (N) بر تقسیم‌کننده (M) را پیدا کنید. خارج قسمت را به شکل یگانی بنویسید و سپس باقی‌مانده را به روش باینری کوتاه بنویسید. در عمل، به یک بیت پایان بعد از خارج قسمت نیاز خواهید داشت: اگر خارج قسمت به صورت دنباله‌ای از صفرها نوشته شده باشد، بیت پایان 1 است (یا برعکس). طول باقی‌مانده می‌تواند با توجه به تقسیم‌کننده تعیین شود.

کد گولومب-رایس، کد گولومبی است که تقسیم‌کننده توانی از 2 باشد. در این شرایط، با استفاده ازعملیات شیفت و ماسک به جای استفاده از تقسیم و باقی‌مانده می‌توان پیاده سازی کاراتری را انجام داد. کد گولومب-رایس برای استفاده بر روی کامپیوتر انتخاب راحت‌تری‌ست زیرا ضرب و تقسیم بر 2 در حساب باینری کاراتر می‌توانند پیاده‌سازی شوند.

برای مثال، در اینجا کد گولومب-رایس با تقسیم‌کننده 4 را برای اعداد 0 تا 15 می‌بینید:

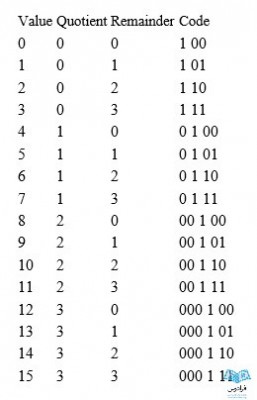
الگوریتم کدگذاری گولومب

تعریف ریاضی مقادیر q و r به صورت است:

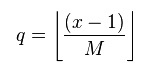
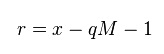
و نتیجه نهایی به این شکل خواهد بود:

توجه کنید که r می‌تواند تعداد متفاوتی بیت داشته باشد: در کد گولومب-رایس تنها b بیت است، و در کد گولومب (یعنی M توانی از 2 نباشد) بین b-1 تا b تعداد بیت می‌تواند باشد. فرض کنید داریم:

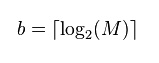
اگر       ،آنگاه از b-1 بیت برای نمایش r استفاده کنید و اگر       ، از b بیت برای نمایش r استفاده کنید. (واضح است که         است اگر M توانی از 2 باشد، و بنابراین در این شرایط می‌توان تمام مقادیر r را با b بیت نمایش دهیم/رمزگذاری کنیم.

این مراحل را می‌توان در الگوریتم زیر به صورت خلاصه چنین نوشت:

1- مقدار M را به یک مقدار صحیح گرد کنید.

2- برای N (عددی که قرار است رمزگذاری شود) این دو مقدار را به دست بیاورید:

•  q
•  r

3- کلمه رمز را تولید کنید:

•  قالب کد به صورت <کد باقی‌مانده><کد خارج قسمت> است که در آن:
•  کد خارج قسمت (با کدگذاری یگانی) به این صورت نوشته می‌شود:
  1. یک رشته به طول q از بیت 1 بنویسید.
  2. یک بیت 0 بنویسید.
•  کد باقی‌مانده (با روش کدگذاری باینری کوتاه) به این صورت نوشته می‌شود:
  1. اگر M توانی از 2 است، باقی‌مانده را به قالب باینری بنویسید. در این صورت به بیت نیاز است (کد گولومب-رایس).
  2. اگر M توانی از 2 نیست، قرار دهید.

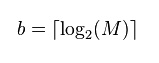
1- اگر   باشد، r را با استفاده از b-1 بیت به صورت باینری ساده کد کنید.
2- اگر    باشد،    را با b بیت به طریق باینری ساده کد کنید.