الگوریتم کوتاه ترین مسیر دایجسترا در سوئیفت — به زبان ساده

گراف‌ها به دلیل انعطاف‌پذیری در طیف وسیعی از اپلیکیشن‌ها شامل سرویس‌های مبتنی بر نقشه، شبکه‌بندی و رسانه‌های اجتماعی کاربرد دارند. مدل‌های رایج می‌تواند شامل جاده، ترافیک، افراد و مکان باشد. در این مقاله به بررسی شیوه جستجوی یک گراف می‌پردازیم و یک الگوریتم محبوب به نام کوتاه ترین مسیر دایجسترا در سوئیفت پیاده‌سازی می‌کنیم.

ایجاد اتصال

چالش ما با گراف‌ها این است که باید شیوه ارتباط با دیگر شیءها را بدانیم. برای نمونه وب‌سایت شبکه اجتماعی LinkedIn را در نظر بگیرید. در LinkedIn هر پروفایل را می‌توان به عنوان یک رأس منفرد تصور کرد که می‌تواند به رئوس دیگر وصل شود. یک قابلیت LinkedIn توانایی معرفی خود به افراد دیگر است. در این سناریو، LinkedIn امکان مسیریابی پیام را از طریق اتصال مشترک فراهم می‌سازد.

فیلم آموزش برنامه نویسی سوئیفت – برنامه نویسی iOS با Swift در فرادرس

کلیک کنید

در نظریه گراف، بهینه‌ترین روش برای تحویل پیام به نام کوتاه‌ترین مسیر نامیده می‌شود.

یافتن روش

کوتاه‌ترین مسیر می‌تواند به عنوان سرویس‌های مبتنی بر نقشه مانند Google Maps نیز نگریسته شود. کاربران به طور مکرر از Google Maps برای یافتن مسیر راندگی بین دو نقطه استفاده می‌کنند، چنان که می‌دانیم در اغلب موارد چند راه برای رسیدن به هر مقصد وجود دارد. کوتاه‌ترین مسیر در اغلب موارد به عوامل مختلفی مانند ترافیک، شرایط جاده، تصادف‌ها و زمان روز بستگی دارد. در نظریه گراف این عوامل خارجی نماینده وزن یال هستند.

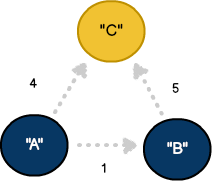
این مثال برخی نکات کلیدی مربوط به الگوریتم دایجسترا را نشان می‌دهد. علاوه بر این راه‌های چندگانه برای رفتن از A به C، کوتاه‌ترین مسیر از طریق B تصور می‌شود. تنها زمانی که از طریق B به نقطه C برسیم می‌توانیم تفسیر خود را از کوتاه‌ترین مسیر و تغییر جهت مورد تعدیل قرار دهیم. این تغییر در جهت به نام «رویکرد حریصانه» (greedy approach) خوانده می‌شود و برای مسائل مشابهی مانند «فروشنده دوره‌گرد» مورد استفاده قرار می‌گیرد.

معرفی الگوریتم دایجسترا

الگوریتم دایجسترا در سال 1959 معرفی شده و برای یافتن کوتاه‌ترین مسیر بین دو رأس در یک گراف جهت‌دار بدون وزن‌های یال غیر منفی مورد استفاده قرار می‌گیرد. در ادامه شیوه پیاده‌سازی آن را در سوئیفت مورد بررسی قرار می‌دهیم.

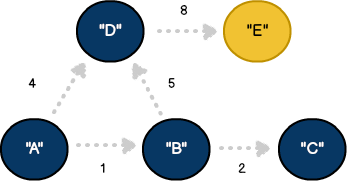
با این که مدل ما با مقادیر کلیدی و وزن‌های یال‌های برچسب خورده است، الگوریتم تنها می‌تواند زیرمجموعه‌ای از این اطلاعات را ببیند. با آغاز از رأس مبدأ، هدف ما پیمایش کل گراف است.

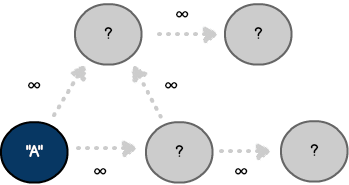
استفاده از مسیرها

در این سفر ما هر گرهی را که در یک ساختمان داده سفارشی بازدید می‌کنیم، مسیر می‌نامیم. مجموع نهایی از تجمیع وزن یال‌هایی که برای رسیدن به مقصد مشخص طی می‌شوند به دست می‌آید. مشخصه previous مسیر انتخابی برای رسیدن به رأس را نمایش خواهد داد:

1//the path class maintains objects that comprise the "frontier"
2class Path {
3    
4    var total: Int
5    var destination: Vertex
6    var previous: Path?
7//object initialization
8    init(){
9        destination = Vertex()
10        total = 0
11    }    
12}

تجزیه دایجسترا

اینک که همه مؤلفه‌های گراف در جای خود هستند، به بررسی الگوریتم دایجسترا می‌پردازیم. متد processDijkstra رئوس مبدأ و مقصد را به عنوان پارامتر می‌گیرد. همچنین یک مسیر (path) بازگشت می‌دهد. از آنجا که ممکن است مکان یافتن یک مقصد وجود نداشته باشد، مقدار بازگشتی به در سوئیفت به صورت optimal اعلان می‌شود:

1//Dijkstra’s shortest path algorithm
2func processDijkstra(source: Vertex, destination: Vertex) -> Path? {
3...
4}

ساخت frontier

چنان که قبلاً گفتیم، کلید درک الگوریتم دایجسترا دانستن شیوه پیمایش گراف است. برای کمک به درک آن چند قاعده و یک مفهوم جدید به نام frontier را معرفی می‌کنیم:

1        var frontier = Array<Path>()
2        var finalPaths = Array<Path>()
3          
4        //use source edges to create the frontier
5        for e in source.neighbors {
6            
7            let newPath: Path = Path()
8         
9          newPath.destination = e.neighbor
10            newPath.previous = nil
11            newPath.total = e.weight
12            
13            //add the new path to the frontier
14            frontier.append(newPath)
15            
16        }

الگوریتم با بررسی رأس مبدأ و تکرار روی لیستی از همسایگی‌ها آغاز می‌شود. می‌دانیم که هر همسایه نماینده یک یال است. در هر تکرار اطلاعاتی در مورد یال همسایه برای ساخت مسیر جدید مورد استفاده قرار می‌گیرد. در نهایت هر مسیر به frontier اضافه می‌شود:

1...
2//construct the best path
3var bestPath: Path = Path()        
4        
5while frontier.count != 0 {
6            
7  //support path changes using the greedy approach
8  bestPath = Path()
9  var pathIndex: Int = 0
10    for x in 0..<frontier.count {
11               
12      let itemPath: Path = frontier[x]
13                
14         if (bestPath.total == 0) || (itemPath.total < bestPath.total) {
15            bestPath = itemPath
16            pathIndex = x
17         }
18                
19   }
20...

چنان که می‌بینید از bestPath برای ساخت یک سری از مسیرها استفاده کرده‌ایم. همچنین سابقه بازدیدهای خود را در مورد هر شیء جدید حفظ می‌کنیم. زمانی که این بخش کامل شد، به بررسی تغییرات frontier می‌پردازیم:

در این مرحله در مورد گراف دانش بیشتری کسب کردیم. اکنون دو مسیر احتمالی دیگر به رأس D وجود دارد. به این ترتیب کوتاه‌ترین مسیر برای رسیدن به رأس D نیز تغییر یافته است. در نهایت مسیری که از A-B می‌گذرد حذف و به ساختار جدیدی که finalPaths نام دارد اضافه می‌شود.

یک مبدأ منفرد

الگوریتم Dijkstra را می‌توان به صورت «مبدأ منفرد» توصیف کرد، زیرا مسیر را به هر رأس محاسبه می‌کند. در مثالمان این اطلاعات را در آرایه finalPaths حفظ می‌کنیم.

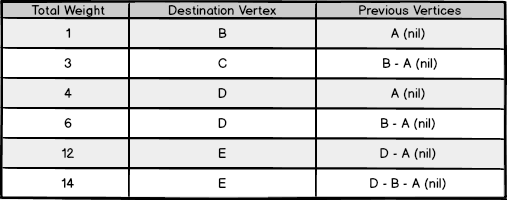
بر اساس این داده‌ها می‌توانیم ببینیم که کوتاه‌ترین مسیر به رأس E از A مسیر A-D-E است. مزیت افزوده آن این است که علاوه بر به دست آوردن این اطلاعات برای یک مسیر مبدأ، کوتاه‌ترین مسیر برای هر گره در گراف را نیز محاسبه کرده‌ایم.

الگوریتم دایجسترا یک راه‌حل عالی برای حل مسئله‌های پیچیده است. با این ما که آن را به روش مؤثری استفاده کردیم، اما امکان بهبود عملکرد آن از طریق برخی تغییرات باز هم وجود دارد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌‌نویسی
• آموزش برنامه‌نویسی Swift (سوئیفت) برای برنامه نویسی iOS
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• آموزش سوئیفت (Swift) — مجموعه مقالات مجله فرادرس
• عملگرهای سفارشی در سوئیفت — از صفر تا صد

==