مفاهیم مقدماتی حسابان (بخش دوم) — با مثالهای عملی

در بخش قبلی این راهنما «مفاهیم مقدماتی حسابان — به زبان ساده» بیان کردیم که حسابان را میتوان یک نوع بینایی اشعه ایکس یا بینایی تایملپس دانست. برای نمونه یک دایره را به صورت مثلثی متشکل از نوارهای کم عرض ترسیم کردیم و بدین ترتیب موفق شدیم به روشی سادهتر مساحت آن را محاسبه کنیم. البته شاید این روش را نتوان سادهتر دانست؛ اما در هر حال درک آن آسانتر بوده است.
اگر محافظهکاری خود را کنار بگذاریم،، میبینیم که دایرهها صرفاً از نوارهای کم عرض ساخته نشدهاند؛ بلکه میتوان خلاقیت بیشتری به کار گرفت و روشهای مختلف دیگری برای مشاهده دایره زیر اشعه ایکس تصور کرد:
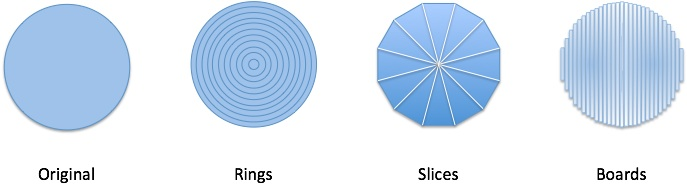
میتوان یک دایره را به صورت مجموعهای از حلقهها، قاچهای پیتزا، یا برشهای عمودی تصور کرد. هر یک از این حالتها یک راهبرد عملی مختلف به صورت گام به گام ارائه میکنند.
تحلیل حلقه به حلقه
اگر از بینایی تایملپس خود کمک بگیریم میبینیم که راهبرد حلقه به حلقه در طی زمان تجمیع میشود:

این فرایند پیشروی حلقه به حلقه چه نکته جذابی دارد؟
- هر گام میانی یک «دایره کوچک» کامل برای خود محسوب میشود. یعنی هنگامی که در نیمه راه هستیم همچنان یک دایره داریم که تنها تفاوتش این است که شعاع آن نصف دایره اصلی است.
- هر مرحله یک مقدار افزایشی برای کار است. صرفاً تصور کنید که میخواهیم یک مزرعه دایرهای شکل را شخم بزنیم و این کار را در طی چند روز انجام دهیم. در روز اول، کار خود را از مرکز مزرعه آغاز میکنیم و از مرکز تکان نمیخوریم. روز بعد، کوتاهترین دوری که میتوان زد را شخم میزنیم. سپس شروع به حرکت در دورهای بعدی میکنیم و این دورها رفته رفته بزرگتر میشوند تا این که در روز آخر دوری به وسعت کل مزرعه دایرهای خود را شخم میزنید.
- این نوع کار کاملاً محتمل است و برنامهریزی برای آن بسیار مفید است. اگر بدانیم که هر دور نسبت به دور قبلی یک دقیقه بیشتر طول میکشد، در این صورت دور بیستم، 20 دقیقه طول خواهید کشید.
- بخش بزرگ کار در دور نهایی صورت میگیرد. در 25% ابتدایی تایملپس ما تقریباً هیچ حرکتی نمیکنیم و دورهای خیلی کوچکی میزنیم. در نزدیک انتهای کار با ایجاد دورهای بزرگ کار بسیار بیشتری صورت میگیرد و مسافت تقریباً برابر با دور نهایی است.
اگر کمی عملیتر فکر کنیم ممکن است از خود بپرسیم چرا درختها باید با الگوهای حلقهای رشد کنند؟
یک درخت بزرگ باید از یک درخت کاملاً کوچکتر رشد کند. رشد درخت از طریق ساخت حلقههای متعدد صورت میگیرد که در اغلب موارد دایرههای کاملی را تشکیل میدهند. مراحل رشد درخت به این صورت نیست که ابتدا نیمدایره چپ کامل شود و سپس به تشکیل نیمدایره راست بپردازد.
در واقع بسیاری از فرایندهای طبیعی مانند درخت، استخوان، حباب و غیره که با رشد همراه هستند این رویکرد رشد داخل به بیرون را طی میکنند.
تحلیل قاچ به قاچ

اینک فرایند پیشروی قاچ به قاچ را بررسی میکنیم. موارد زیر در این فرایند قابل توجه هستند:
- در این فرایند رشد در هر مرحله حجم کار یکسانی صورت میگیرد. در واقع همه قاچها با هم برابر هستند. شاید این موضوع از نظر ریاضی چندان مهم نباشد؛ اما در دنیای واقعی (مانند بریدن یک کیک) میخواهیم از حرکت مشابهی برای برش همه قاچها استفاده کنیم.
- از آنجا که قاچها متقارن هستند، میتوانیم از میانبرهایی مانند ایجاد برشهایی در سراسر شکل استفاده کنیم. این خط برش هنگامی که میخواهیم اجزای یکسانی ایجاد کنیم بسیار به کار میآیند.
- در این فرایند اندازهگیری پیشرفت بسیار آسان است. اگر 10 قاچ داشته باشیم، در این صورت در قاچ 6 دقیقاً 60% کار (از نظر محیط و مساحت) صورت گرفته است.
- در این نوع فرایند ما در یک مسیر دایرهای حرکت میکنیم و از نقطه نظر زاویهای هرگز به مکان قبلی بازنمیگردیم. با این حال در رویکرد حلقهای در هر مرحله یک دور کامل، یعنی 360 درجه روی دایره میزدیم.
در دنیای واقعی در موارد زیادی از رویکرد قاچ به قاچ برای پیشروی استفاده میکنیم. برای مثال هنگام تقسیم انواع خوراکیها مانند کیک، پیتزا و هندوانه که میخواهیم هر فرد سهم یکسانی دریافت کند، از رویکرد قاچ کردن استفاده میکنیم. برش قاچها آسان است و میتوان با ایجاد برشهای کلی بهسرعت آن را اجرا کرد. همچنین در هر مرحله، مشاهده این که چه مقدار باقی مانده است، آسان خواهد بود. تصور کنید بخواهید یک کیک را به صورت حلقهای برش دهید و در هر مرحله تخمین بزنید چه مقدار از کیک باقی مانده است.
همچنین در اسکنرهای رادار از روش پیشروی قاچ به قاچ استفاده میشود. این رادارها یک پرتو را به روش قاچ به قاچ در یک دایره ارسال میکنند و پیش از رفتن به قاچ بعدی یک قاچ از آسمان را اسکن میکنند. البته این راهبرد نقاط کوری ایجاد میکند که در هر مرحله اسکن نمیشوند،. با این حال این هزینهای است که باید برای مزیت استفاده از رویکرد قاچ به قاچ پرداخت کرد.
به طور عکس، رادارهای سونار که در زیردریاییها یا از سوی خفاشها استفاده میشود یک موج حلقهای را در تمام جهات پخش میکنند. این وضعیت برای اهداف نزدیک مناسب است و با آن همه جهات در یک مرحله پوشش مییابند و عیب آن این است که این انتشار بدون تمرکز جهتی موجب ضعیفتر شدن موج در فواصل طولانیتر میشود، چون انرژی اولیه با جلوتر رفتن ضعیفتر میشود. در چنین مواردی از آنتنها برای تقویت سیگنالها در قاچهای نازک استفاده میشود تا انرژی موجها متمرکزتر شود.
ازنظر عملی اگر بتوانیم یک شکل دایرهای را از مجموعهای از قاچها بسازیم (برای نمونه بخشهای تا خورده یک فرفره کاغذی) میتوانیم مطمئن باشیم که همه بخشها یکسان هستند. بهترین روش برای ساخت یک قاچ منفرد این است که آنها را به صورت انبوه تولید کنیم. نکته بهتر این است که اگر یک بخش خراب شود، کل شکل میتواند تا بخورد!
تحلیل برش به برش

به روند پیشروی شکل فوق نگاه کنید و چند ثانیه را صرف تأمل در مورد مزایا و معایب آن بکنید. این تأملها را در نکات زیر میتوان جمعبندی کرد.
- این یک فرایند کاملاً منظم است که در آن برشها از چپ به راست کنار هم چیده میشوند.
- مشارکت هر مرحله از کم آغاز میشود و به تدریج بیشتر میشود تا این که در میانه به بیشینه مقدار خود میرسد و سپس مجدداً رو به نقصان میگذارد.
- پیشروی به نوعی غیر قابل پیشبینی تلقی میشود. بدیهی است که در نیمه راه، نیمی از دایره نیز تکمیل شده است؛ اما الگوی فراز و فرود موجب شده است که تحلیل آن دشوار شود. به طور عکس در الگوی حلقه به حلقه، در هر مرحله پیشروی به مقدار مشخصی صورت میگرفت و این مقدار همواره افزایشی بود. روشن است که حلقههای متأخرتر کار بیشتری انجام میدادند. در این نوع پیشروی بیشترین حجم کار از سوی برشهای میانی صورت میگیرد.
در ادامه به بررسی موارد کاربرد این الگو در دنیای واقعی میپردازیم.
یکی از مهمترین مثالها سکوها و سازههای چوبی هستند. زمانی که الوارهای چوبی را کنار هم میچینیم، به هیچ وجه دوست نداریم که دوبارهکاری بکنیم، به خصوص که در اغلب موارد گامهای دیگری مانند نقاشی نیز وجود دارند. همانطور که یک درخت در هر مرحله به یک حلقه کامل نیاز دارد، یک سکوی چوبی نیز به تکمیل شدن به صورت خطی به استفاده از الوارها نیاز دارد.
در واقع هر فرایندی با یک ترتیب صریح، یعنی پایان دادن یک مرحله و بعد رفتن به مرحله بعد، میتواند از این رویکرد بهره بگیرد. برای نمونه یک پرینتر را در نظر بگیرید که هر بار اندکی از کاغذ را به درون خود میکشد و مقادیری جوهر را روی کاغذ اسپری میکند. این پرینتر هر موقعیت را تنها یک بار میبیند.
دایرهای که در این رویکرد نشان دادهایم، لزوماً نمیبایست یک شکل باشد. بلکه میتواند نماینده یک هدف باشد که تلاش میکنید به آن برسید. این هدف میتواند یک برنامه ورزشی یا موضوعاتی باشد که در یک نشست مشاورهای قرار است مطرح شوند.
رویکرد برشی یک شروع کوچک دارد و در ادامه حجم کار بالا میرود و سپس دوباره کاهش مییابد. رویکرد قاچهای پیتزا میتواند یکنواخت باشد و برای اموری که هر روز به پیشرفت یکسانی نیاز دارند مناسب است. رویکرد حلقهای ممکن است موجب تضعیف روحیه شود، چون هر مرحله به تلاش بیشتری نسبت به مرحله قبل نیاز دارد.
سازماندهی کردن
تا به این جا در این راهنما تلاش کردهایم که اندیشههای مورد بحث را با استفاده از توصیفهای طبیعی ارائه کنیم. این مفاهیم با استفاده از مثالهایی مانند دستهای از حلقهها یا قاچهای پیتزا معرفی شدهاند. در ادامه سعی میکنیم این مباحث را کمی سازماندهی بکنیم تا روشنتر شوند.
در آغاز میتوانیم توضیح خود را از شیوه افراز یک دایره به قطعه (مرحله) های مختلف شروع کنیم. تصور کنید دایرهای مانند شکل زیر دارید و آن را در جهتی که فلش نشان میدهد، به قطعههای مختلف برش میزنید.
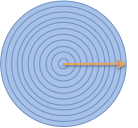
ما در راستای خط زرد حرکت میکنیم. هر بار که به یک مرحله میرسیم آن را جدا میکنیم. در این فرایند با این که فلش شیوه ساخته شدن حلقهها را نشان میدهد؛ اما تصور کردن مراحل دشوار است، زیرا درون دایره فشرده شدهاند. اما همچنان که در بخش قبلی این راهنما مشاهده کردیم، میتوانیم مراحل منفرد را از دایره جدا کرده و آنها را کنار هم به صورت مثلث زیر بچینیم.
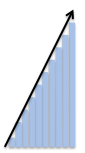
برای این که روند پیشروی کار و اندازه هر گام را نشان دهیم یک فلش سیاه رنگ ترسیم کردهایم. اینک با یک نگاه گذرا میتوان گفت که حلقهها به صورت افزایشی هستند و این افزایش در هر گام به مقدار ثابتی رخ میدهد، چون خط روند شیب ثابتی دارد و مانند یک پلکان است.
بدین ترتیب میتوانیم همه فرایندهایی که در این نوشته معرفی کردیم را نیز به صورت زیر تحلیل کنیم.
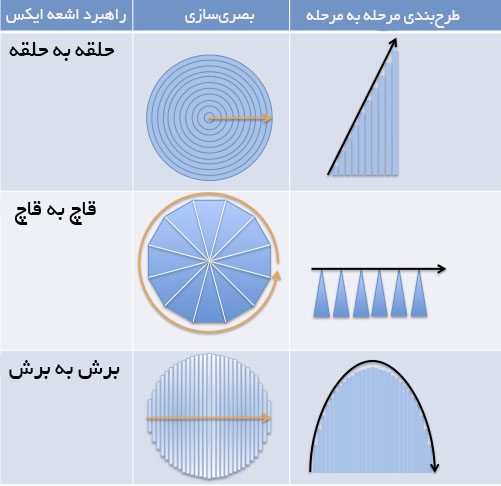
میبینید که مقایسه هر یک از راهبردها در روش اشعه ایکس چه قدر آسانتر شده است.
- در حلقههای مدور، مراحل به صورت تدریجی افزایش مییابند.
- در قاچهای مثلثی همه مراحل اندازه یکسانی دارند.
- در برشهای مستطیلی، مراحل مختلف تا رسیدن به اوج بزرگتر میشوند و سپس در یک فرایند معکوس کوچکتر میشوند. خط روند در این وضعیت طولانیتر به نظر میرسد، زیرا برشها به سمت پایین فشرده شدهاند تا در انتها کنار هم قرار گیرند.
احتمالاً موافق هستید که نمودارهای فوق باعث میشوند کار مقایسه راهبردهای مختلف آسانتر شود. در واقع اگر دقت کنید، خط روند در نمودارهای فوق مشابه همان نمودار مخوف x-y است.
همان طور که میبینید تا کنون در همه کلاسهای ریاضیات صرفاً خط روند به شما نشان داده شده است و گفته نشده که این خط نمایش دهنده کدام قطعات یا مراحل است. بدین ترتیب میبینیم که همواره باید در مورد معنای یک نمودار کنجکاو و صریح باشیم.
خط سیاه روند توصیفی بسیار فشرده از راهبرد اشعه ایکس است. ما به این طریق، اندازه هر مرحله (ارتفاع نمودار) و شیوه تغییر اندازه آن (مدت روند) را نمایش میدهیم. تفاوت بین حلقه، قاچ و برش اهمیتی ندارد، چون در حسابان همه آنها صرفاً بخشهایی از یک الگوی کلی هستند. کلماتی مانند «قاچ»، «حلقه» یا «برش» صرفاً نسخههایی توصیفی از «قطعات یک کل» هستند و در واقع میتوان آنها را با هم تعویض کرد.
در این راهنما ما به تجزیه نمودارها تا سطح خطوط روند و قطعههای منفرد پیش رفتهایم. این مطالب پایهای برای مراحل بعدی مبتنی بر عملکرد هستند که شما در آنها به طور مستقیم با نمودارها سر و کار خواهید داشت. اما باید اشاره کنیم که ارشمیدس بنیانهای اولیه حسابان را بدون استفاده از نمودارهای x-y بنا نهاد و نتایجش را بدون بهرهگیری از آنها به دست آورد. در بخش بعدی (+) این نوشته به بررسی این تحلیلها در فضای سهبعدی خواهیم پرداخت.
برای مطالعه بخش بعدی این مطلب روی لینک زیر کلیک کنید:
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش جامع ریاضی دبیرستان
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- تقلب نامه (Cheat Sheet) مفاهیم و روابط حد و پیوستگی
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
- حد در بینهایت — به زبان ساده
==












