فرمول فشار مایعات چیست؟ – به زبان ساده + حل ۲۰ مثال و تمرین
فشار در مایعات بر اساس قواعد و اصولی مانند اصل پاسکال، معادله برنولی، نیروی شناوری، وزن مایع و ... توصیف میشود که نتیجه آن، فرمولها و روابط مختلفی است. در این مطلب از مجله فرادرس انواع فرمول فشار مایعات را به زبانی ساده و همراه با حل مثالها و تمرینهای متنوع معرفی میکنیم.
- با فرمولهای فشار مایعات آشنا خواهید شد.
- میآموزید فشار در مایعات ساکن و مایعات در حال حرکت چه تفاوتی با هم دارند.
- با اصل پاسکال و کاربردهای آن در انتقال فشار مایعات آشنا خواهید شد.
- اصل برنولی و تاثیر سرعت مایعات روی فشار آنها را خواهید شناخت.
- اثر نیروی شناوری و وزن جسم را در بررسی غوطهوری آن در یک مایع متوجه خواهید شد.
- با حل سوالات متنوع نحوه بکارگیری فرمول فشار مایعات را تمرین خواهید کرد.

به همین منظور، در اولین بخش دستهبندی اصلی فرمول فشار مایعات را بر مبنای ساکن یا متحرک بودن آنها توضیح میدهیم. سپس به تشریح تفاوتهای فشار استاتیک و دینامیک خواهیم پرداخت. بخش بعدی به توضیح اصل پاسکال و مفهوم انتقال فشار در مایعات اختصاص دارد. در ادامه در مورد نیروی شناوری، فشار در لولههای U شکل و معادله برنولی صحبت خواهیم کرد. همچنین با حل ۲۰ مثال و تمرین در قالب سوالات تشریحی و چهار گزینهای به شما کمک خواهیم کرد تا به این مبحث کاملا مسلط شوید.
فرمول فشار مایعات
برای اینکه فرمول فشار مایعات را دقیقتر بدانیم، باید تفاوت فشار در مایعات ساکن و متحرک را در نظر بگیریم. فشار یک مایع ساکن و بدون حرکت از وزن آن ناشی میشود و در نتیجه فقط به عمق یا ارتفاع مایع ()، چگالی آن () و اندازه شتاب گرانش زمین () بستگی دارد. به این ترتیب فرمول فشار مایعات ساکن یا برابر است با . اما اگر همین مایع با سرعت شروع به حرکت کند، فشار دینامیکی یا آن توسط فرمول محاسبه میشود.
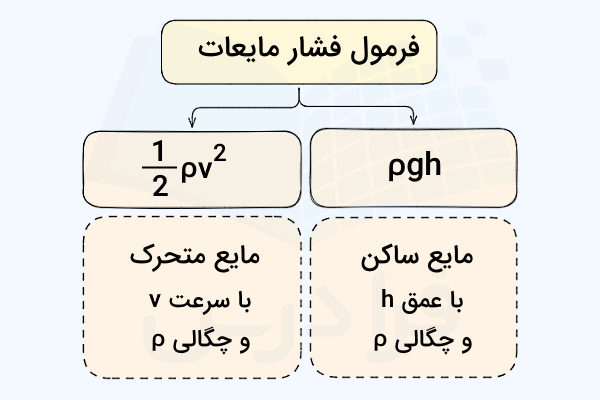
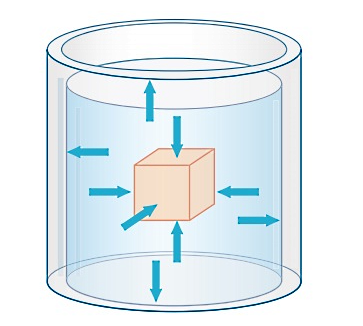
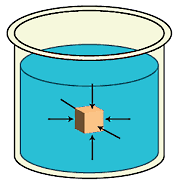
بنابراین انتخاب درست فرمول فشار مایعات در اولین قدم به این بستگی دارد که مایع موردنظر ما ساکن است یا در حال حرکت. در ادامه این بخش انواع فرمول فشار مایعات را بیشتر توضیح میدهیم. در مورد فشار یک مایع ساکن، باید بدانیم نیرویی که بر اثر فشار مایع بر جسم غوطهور داخل آن و بر دیوارههای یک ظرف وارد میشود، همواره عمود بر سطح است. شکل زیر عمود بودن این نیرو را نشان میدهد:
یک آزمایش برای بررسی اثر فشار مایعات و جهت آن این است که یک بادکنک پر از هوا را در ظرف آبی فرو کنیم. مشاهده خواهیم کرد که با ول کردن بادکنک، بلافاصله به سمت بالا میآید و روی آب شناور میماند. بنابراین آب (یا هر مایع دیگری) در جهت رو به بالا نیز فشار وارد میکند. به همین ترتیب فشار مایعات روی سطوح جانبی نیز اثر دارد. اگر یک بطری پر از آب را از پهلو سوراخ کنیم، آب با سرعت از سوراخ بیرون میریزد، چرا که مایع بر دیوارههای ظرف فشار جانبی وارد میکند.
فرمول فشار استاتیک
فشار استاتیکی یا فشار ایستا همان فشار مایعات ساکن و بدون حرکت است. این نوع فشار که در حالت کلیتر برای انواع سیالات ساکن شامل مایعات و گازهای ساکن فشار هیدرواستاتیک نامیده میشود، معادل است با نیروی وارد شده توسط مایع ساکن بر واحد سطح. نیروی وارد شده از طرف مایع بر دیوارههای یک ظرف یا جسمی که در داخل آن غوطهور شده است، مثالهایی از این نوع فشار هستند.
این فشار نتیجه حرکت تصادفی و برخورد مولکولهای مایع با دیوارههای ظرف یا جسم غوطهور در آن است و بهصورت ایزوتروپیک عمل میکند، به این معنا که اثر آن در تمام جهات یکسان است. فرمول فشار استاتیک در عمق مشخصی از یک ستون مایع به صورت زیر تعریف میشود:
- : فشار مایعات ساکن یا استاتیک بر حسب پاسکال ()
- : چگالی مایع بر حسب کیلوگرم بر متر مکعب ()
- : شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه ()
- : عمق یا ارتفاع مایع بر حسب متر ()
- : فشار جو یا فشار اتمسفر بر حسب پاسکال ()
دقت کنید در رابطه بالا فشار سطح باز یا سطح آزاد مایع است. این فشار همان فشار اتمسفر است که میدانیم مقدار عددی آن به شکل تقریبی همواره برابر است با:
نکته: در فرمول بالا بخش همان فشار پیمانهای (فشار نسبی یا فشار گیج) مایع است. به این ترتیب فرمول بالا به شکل زیر خواهد شد:
در نتیجه فشار استاتیکی نیز همان فشار مطلق خواهد بود. میدانیم فشار مطلق فشاری است که نسبت به خلاء کامل اندازهگیری میشود و از جمع کردن فشار پیمانهای و فشار اتمسفر به دست میآید. پس فشار در مایعات یا فشاری که یک مایع به یک نقطه وارد میکند، به عوامل زیر بستگی دارد:
- عمق مایع
- چگالی مایع
- شتاب گرانش زمین
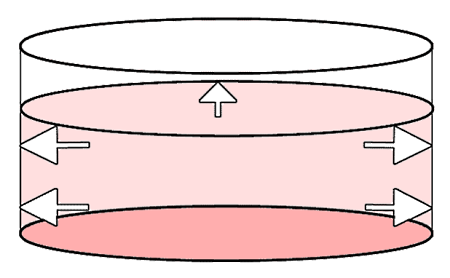
آزمایش زیر نشان میدهد که در یک عمق مشخص، فشار مستقل از جهت بوده و در همه جهات یکسان است. به همین دلیل فشارسنجها مقدار یکسانی را نشان میدهند چون فشار در یک عمق معین (خط قرمز) ثابت است:
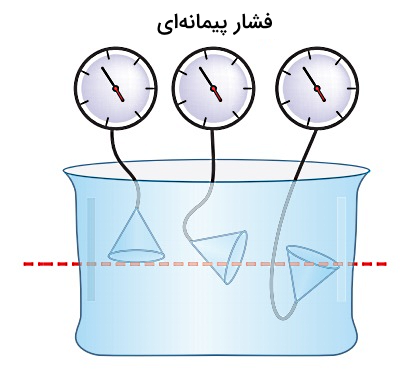
روش محاسبه فرمول فشار مایعات ساکن
اگر بخواهیم فرمول فشار مایعات ساکن را با توجه به فرمول اصلی فشار یعنی پیدا کنیم، کافی است طبق شکل زیر فشار ناشی از وزن یک ستون مایع بدون حرکت را در نظر بگیریم که دارای سطح مقطعی برابر با و عمق است. میدانیم فرمول نیروی وزن برابر است با حاصلضرب جرم در شتاب جاذبه زمین. بنابراین فرمول فشار برای مایعات ساکن به شکل زیر ساده میشود:
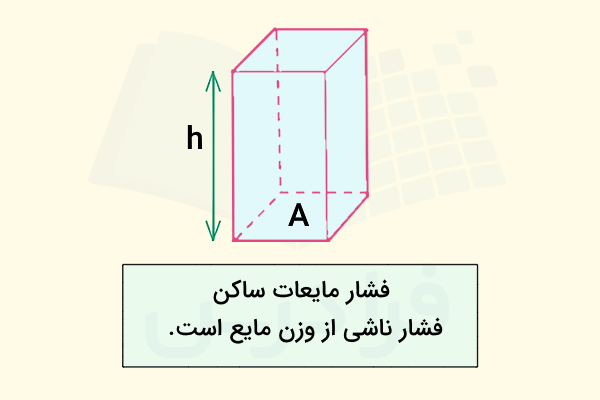
حالا با توجه به فرمول چگالی به شکل ، میتوانیم به جای جرم یا در رابطه بالا از حاصلضرب چگالی در حجم استفاده کنیم:
همانطور که اشاره شد، در این محاسبات ستون مایع را به شکل استوانهای با سطح مقطع و ارتفاع در نظر گرفتهایم. طبق فرمول حجم استوانه، میتوانیم حاصلضرب سطح مقطع در ارتفاع را جایگزین در رابطه بالا کنیم:
به این ترتیب با حذف فرمول فشار مایعات ساکن به دست آمد و ملاحظه میکنید که طبق این فرمول، فشار فقط و فقط به عمق یا ارتفاع مایع ساکن، چگالی آن و مقدار شتاب گرانش زمین که همواره برابر است با ، بستگی دارد. یک نکته جالب در مورد فرمول فشار مایعات ساکن پارامترهایی است که در آن وجود ندارد. برای مثال فشار مایع ساکن به جرم، حجم یا شکل ظرفی که داخل آن است، بستگی ندارد. در تصویر زیر با اینکه شکل ظروف متفاوت است، اما اگر مایع یکسانی را در هر سه ظرف تا عمقی برابر با بریزیم، فشار یکسانی به اندازه خواهیم داشت:
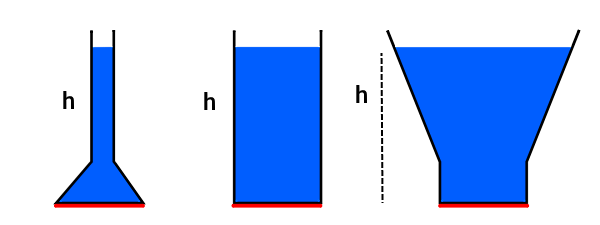
دقت کنید به دلیل ساده بودن تصور یک ستون مایع با ارتفاع مشخص، بهتدریج رایج شد که انواع فشار را بر حسب ارتفاع ستون مایع بیان کنند و در نتیجه از واحدهای دیگری مانند میلیمتر جیوه (mmHg) یا سانتیمتر آب (cm H₂O) نیز در کنار واحد استاندارد فشار یعنی پاسکال (Pa) استفاده شد. همچنین فشار مایعات اغلب توسط مانومترها و بر اساس ارتفاع ستون مایع اندازهگیری میشوند.
فرمول فشار دینامیک
در بخش قبل آموختیم فرمول فشار مایعات ساکن یا فشار استاتیک چیست. در این بخش توضیح میدهیم اگر مایعی ساکن نباشد، فشار آن چگونه محاسبه میشود. فشاری که در یک سیال در حال حرکت به علت حرکت یا سرعت آن وجود دارد، فشار دینامیکی یا نامیده میشود. این فشار برابر است با انرژی جنبشی بر واحد حجم مایع و فرمول آن به شکل زیر است:
- : فشار مایعات متحرک بر حسب پاسکال ()
- : چگالی مایع بر حسب کیلوگرم بر متر مکعب ()
- : سرعت مایع بر حسب متر بر ثانیه ()
فرض کنید مطابق تصویر زیر مایعی در یک لوله افقی با سرعت جریان دارد. شاید بنظر برسد که طبق تعاریف چون مایع سرعت دارد پس فشار استاتیک نداریم، اما این نگرش درست نیست. در حقیقت فشار استاتیک در این مثال به صورت عمود بر سطح مایع اندازهگیری میشود و به همین علت مقدار آن به جهت جریان وابسته نیست. اگر دقت کنید اینکه جریان مایع در لوله افقی با چه سرعتی در حال حرکت است، روی بخشی از مایع که در ستون عمودی سمت چپ و در حالت سکون قرار گرفته است، تاثیری ندارد. فشار ناشی از این ستون فقط به وزن مایع بستگی دارد.
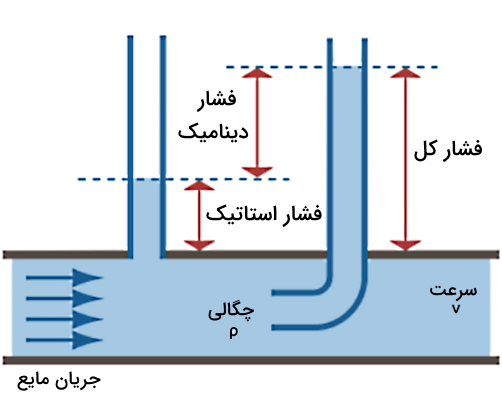
اما فشار دینامیک فشاری است که از حرکت مایع ایجاد میشود. بنابراین این فشار موازی با جهت جریان اندازهگیری شده و به سرعت آن بستگی دارد. در نتیجه برای اندازهگیری یا مشخص کردن فشار دینامیک لازم است از یک لوله خمیده شبیه لوله U شکل نصف شده استفاده کنیم و آن را در معرض جریان مایع قرار دهیم. به این ترتیب سطح مایع در ستون عمودی سمت راست بسته به سرعت حرکت آن تغییر خواهد کرد.
بنابراین در یک مایع متحرک یا در حال جریان، فشار کل در هر نقطه برابر است با مجموع فشار استاتیک و دینامیک در آن نقطه. این رابطه در حقیقت شکل ساده شده معادله برنولی برای یک جریان افقی است که در بخشهای بعد بیشتر راجعبه آن توضیح خواهیم داد. معادله برنولی رابطه معکوسی که بین فشار استاتیک و دینامیک در طول یک خط جریان وجود دارد را توضیح میدهد، به این شکل که اگر سرعت جریان زیاد شود، فشار دینامیکی نیز افزایش مییابد، در حالی که فشار استاتیکی کاهش پیدا میکند تا فشار کل ثابت بماند.
یادگیری فرمول فشار مایعات با فرادرس
در این بخش قصد داریم به معرفی چند فیلم آموزشی از مجموعه فرادرس برای دانشآموزان بپردازیم. همانطور که میدانید، در کتاب علوم تجربی پایه نهم، درسی با عنوان «فشار و آثار آن» و در کتاب فیزیک پایه دهم در مبحثی با عنوان «ویژگیهای فیزیکی مواد» در مورد فشار صحبت شده است. بنابراین مشاهده فیلمهای آموزشی مربوط به این کتابهای درسی به شما کمک میکند تا با دیدن تصاویر و شنیدن توضیحات بیشتر، درک بهتری نسبت به فرمولهای فشار از جمله فرمول فشار مایعات بهدست آورید:
- فیلم آموزش رایگان دانسیته یا چگالی چیست؟ – از فرمول تا محاسبه عملی فرادرس
- فیلم آموزش رایگان چرا کشتی روی آب میماند؟ + از چگالی تا نیروی ارشمیدس فرادرس
- فیلم آموزش رایگان قانون ارشمیدس چیست؟ + کاربرد و مفهوم شناوری و چگالی فرادرس
- فیلم آموزش رایگان فرمول فشار چیست؟ + معادله برنولی + مثال فرادرس
قانون پاسکال و انتقال فشار
اصل پاسکال یا قانون پاسکال به افتخار نام «بلز پاسکال» (Blaise Pascal) ریاضیدان و فیزیکدان فرانسوی نامگذاری شده است. این قانون بیان میکند که فشار خارجی وارد شده به یک مایع تراکمناپذیر به صورت یکنواخت در سرتاسر آن منتقل میشود. قانون پاسکال را میتوان با استفاده از یک ظرف شیشهای که در تمام سطح آن سوراخهایی وجود دارد نشان داد. به تصویر زیر دقت کنید:
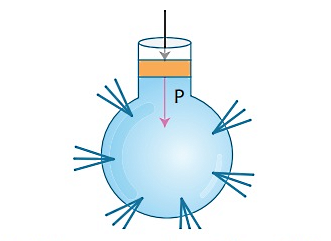
ظرف کروی شکلی را از آب پر کنید. سپس پیستون بخش بالای آن را به سمت پایین فشار دهید. آب با فشاری برابر با فشار وارد بر پیستون از سوراخهای ظرف به بیرون میجهد. در واقع نیرویی که بر پیستون وارد میکنید، فشاری را بر آب اعمال میکند و این فشار بهطور مساوی در همه جهات درون مایع منتقل میشود. از این اصل در ماشینهای مختلفی که در زندگی روزمره بکار میبریم از جمله در جکهای هیدرولیکی استفاده میشود.
جک هیدرولیکی
قانون پاسکال یکی از مهمترین اصولی است که در طراحی ماشینی به نام جک هیدرولیکی استفاده شد. این وسیله از دو سیلندر با سطح مقطعهای متفاوت طبق تصویر زیر ساخته میشود. درون این سیلندرها پیستونهایی با سطح مقطعهای و قرار دارند. عموما جسم سنگینی که قرار است بالا رود، روی پیستون بزرگتر با سطح مقطع گذاشته میشود:
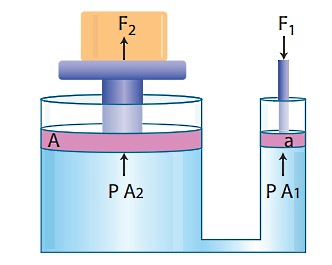
عملکرد جک هیدورلیکی به این صورت است که ابتدا نیروی بر پیستونی با سطح مقطع کوچکتر یعنی وارد میشود. سپس فشار که توسط این پیستون کوچک ایجاد شده است، بهطور یکنواخت و از طریق مایع مشترک بین دو سیلندر به پیستون بزرگتر منتقل میشود. این مسئله نتیجه اصل پاسکال است. بنابراین نیروی که مقدار آن بسیار بیشتر از نیروی است، بر سطح مقطع بزرگتر یعنی وارد میشود و در صورتی که روی این سطح بار سنگینی قرار گرفته باشد، امکان بلند کردن این بار توسط این نیروی بزرگ فراهم خواهد شد.
پس جک هیدرولیکی مثال مرسومی است از کاربرد اصل پاسکال. در واقع طبق این قانون، فشار وارد بر پیستون کوچکتر بدون هیچ کم و کاستی به پیستون بزرگتر منتقل میشود. بنابراین داریم:
مقایسه دو کسر بالا ما را به این نتیجه میرساند که در جک هیدرولیکی با اعمال نیروی ، نیروی با مقدار دریافت خواهیم کرد و چون در طراحی این جک همواره نسبت بزرگتر از یک است، پس نیروی بیشتری به دست خواهیم آورد. بر همین اساس سیستمهای جک هیدرولیکی به سیستمهای چند برابر کننده نیرو نیز معروفاند. اگر تمایل دارید در مورد مکانیک حاکم بر مایعات و در سطح کلیتر سیالات، اطلاعات بیشتری کسب کنید، پیشنهاد میکنیم مطلب «مکانیک سیالات چیست؟ – مفاهیم پایه به زبان ساده + منابع یادگیری» از مجله فرادرس را مطالعه کنید.
نیروی شناوری چیست؟
احتمالا تا به حال این مسئله را مشاهده کردهاید که اگر جسمی به طور جزئی یا کامل در مایعی غوطهور شود، بر اثر فشار مایع اطراف خود نیرویی به سمت بالا را تجربه میکند. در این آزمایش همواره فشار در قسمت پایین مایع بیشتر و در قسمت بالای آن کمتر است. در واقع این اختلاف فشار باعث میشود که نیرویی به نام نیروی شناوری یا Buoyant Force بر جسم وارد شده و آن را به سمت بالا هل دهد.
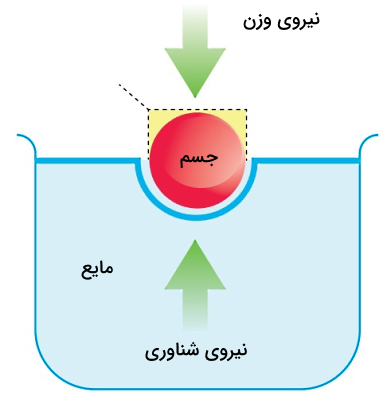
نیروی شناوری همواره در رقابت با وزن جسم است، یعنی اگر وزن جسم کمتر از مقدار آبی باشد که جابجا کرده است (یا اگر چگالی جسم کمتر باشد)، اثر نیروی شناوری بیشتر است و در نتیجه جسم روی مایع شناور میماند (چنین جسمی را شناور مثبت نیز مینامند). اما اگر وزن جسم بیشتر از مقدار آبی باشد که جابجا کرده است (یعنی چگالی آن بیشتر باشد)، اثر نیروی شناوری کمتر است و جسم به زیر آب فرو میرود (چنین جسمی را شناور منفی نیز مینامند).
نمایش ریاضیاتی یا فرمول نیروی شناوری به شکل زیر تعیین میشود:
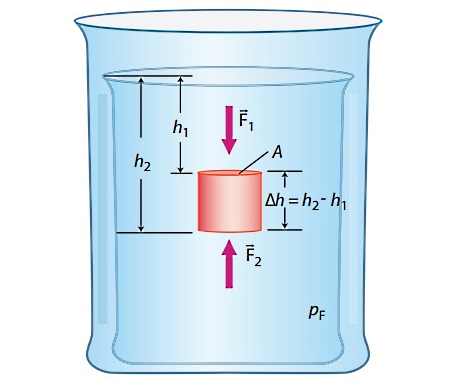
جسم بالا را که در یک مایع غوطهور است، در نظر بگیرید. نیروی خالص وارد بر آن همان نیروی شناوری است که از اختلاف دو نیروی و ناشی میشود:
از طرفی میدانیم فشار مایعات ساکن برابر است با . پس فرمول بالا به شکل زیر نوشته میشود:
با نوشتن ، در نهایت به فرمول زیر برای نیروی شناوری میرسیم:
به عبارت دیگر فرمول نیروی شناوری برابر است با حاصلضرب شتاب جاذبه زمین در حجم مایع جابجا شده در چگالی مایع.
اصل ارشمیدس
اصل ارشمیدس در حقیقت نتیجهای از قانون پاسکال است. طبق این اصل هرگاه جسمی در مایعی غوطهور شود، یک نیروی شناوری عمودی و رو به بالا را تجربه میکند که با وزن مایعی که جسم جابهجا کرده برابر است. به این ترتیب در اثر این نیروی شناوری، جسم بهطور ظاهری بخشی از وزن خود را از دست میدهد و این کاهش وزن ظاهری دقیقا با مقدار نیروی شناوری وارد بر جسم برابر است.
فشار مایعات در لوله های U شکل
بخشی از معروفترین مسائل در حوزه فشار مایعات مربوط میشود به لولههای U شکل. استفاده از این لولهها روش سادهای برای اندازهگیری فشار است. برای نمونه، مانومتر یک لوله U شکل است که از مایعی با چگالی معلوم پر میشود. اگر فشار در دو سر باز لوله U شکل برابر باشند، در این صورت سطح مایع در هر دو طرف یکسان است:
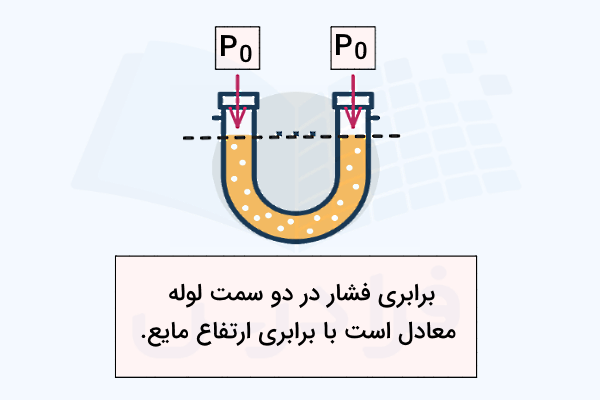
اما اگر فشار در یکی از دو سمت افزایش پیدا کند، مایع در آن قسمت پایین میرود و در سمت دیگر بالا میآید. در این شرایط، اختلاف ارتفاع بین دو سطح نشان دهنده اختلاف فشار بین دو انتهای لوله است.
پیشنهاد میکنیم در این زمینه فیلم آموزش رایگان روش حل لولههای U شکل + محاسبه فشار مایعات فرادرس را مشاهده کنید که لینک آن نیز برای دسترسی راحتتر شما در ادامه قرار داده شده است:
به این ترتیب اگر دو مایع با چگالیهای متفاوت و که قابلیت مخلوط شدن ندارند را در دو شاخه یک لوله U شکل بریزیم، مایعی که چگالی بیشتری دارد، به پایین میرود و مایع با چگالی کمتر روی آن قرار میگیرد. یک مثال خوب در این زمینه، مخلوط سرکه و روغن است. سرکه چگالی بیشتری نسبت به روغن دارد و بنابراین در پایین قرار میگیرد و روغن روی آن میماند. حالا اگر این دو مایع را در دو بازوی لوله U شکل بریزیم، آنها به شکل زیر در لوله به تعادل میرسند:
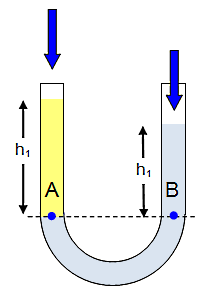
مایع چگالتر در پایین و مایع سبکتر در بالا قرار میگیرد. از آنجا که طبق اصل پاسکال، فشار در یک عمق مشخص درون یک مایع در تمام نقاط یکسان است، ارتفاع دو ستون مایع بالای نقطه مشخص شده باید فشارهای مساوی وارد کنند:
اصل برنولی (فشار مایعات در حال حرکت)
اصل برنولی یا Bernoulli’s Principle بیان میکند که مجموع انرژی مکانیکی یک سیال روان (از جمله مایعات) در سراسر جریان ثابت باقی میماند. به عبارت دیگر، افزایش سرعت یک مایع همیشه همراه است با کاهش فشار یا انرژی پتانسیل آن. پس اگر مایعی جریان آرامی دارد، فشار بیشتری وارد میکند، در مقایسه با مایعی که سریعتر جریان دارد.
معادله برنولی
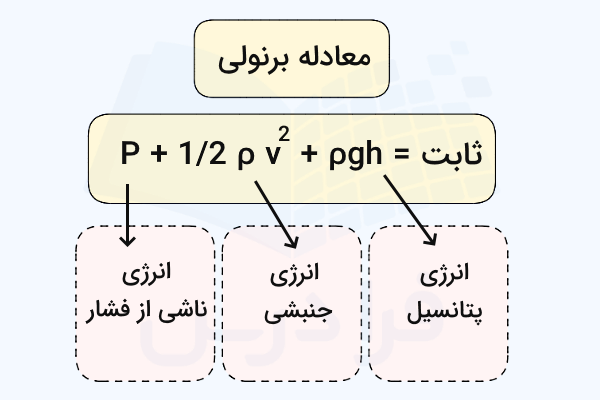
معادله برنولی معادلهای است که بر مبنای اصل برنولی قانون پایستگی انرژی را در مورد جریانهای پایایی از سیالات تراکمناپذیر (مانند آب) توضیح میدهد. این معادله انرژی مایع را بر حسب فشار، سرعت و ارتفاع آن بیان میکند و نامگذاری آن بر اساس کارهای ریاضیدان و فیزیکدان سوئیسی «دانیل برنولی» (Daniel Bernoulli) انجام شده است. البته خود معادله برنولی توسط ریاضیدان و فیزیکدان سوئیسی دیگری به نام «لئونارد اویلر» (Leonhard Euler) بعدها استخراج شد. این معادله به صورت زیر است:
ثابت
- : فشار مایعات ساکن یا فشار استاتیکی بر حسب پاسکال ()
- : چگالی مایع بر حسب کیلوگرم بر متر مکعب ()
- : شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه ()
- : عمق یا ارتفاع مایع بر حسب متر ()
- : سرعت مایع بر حسب متر بر ثانیه ()
دقت کنید این معادله برای تمام سیالات یا شارهها برقرار است، اما ما در این مطلب فقط روی مایعات تمرکز داریم و به همین علت تعاریف را برای مایعات نوشتهایم. معادله برنولی از سه جمله تشکیل شده که مجموع آنها انرژی مکانیکی سیال را تشکیل میدهد. همچنین واحد هر جمله در این معادله همان واحد استاندارد فشار یعنی پاسکال است:
- جمله اول یا انرژی ناشی از فشار مایع است.
- جمله دوم یا انرژی جنبشی حاصل از حرکت مایع است.
- جمله سوم یا انرژی پتانسیل گرانشی ناشی از ارتفاع یا عمق مایع است.
ثابت ماندن مجموع این سه جمله به این معنا است که میتوانیم با در نظر گرفتن دو نقطه مشخص ۱ و ۲ در داخل لولهای که یک مایع از آن عبور میکند و بکارگیری اندیسهای مناسب، معادله برنولی را به صورت زیر نیز بنویسیم:
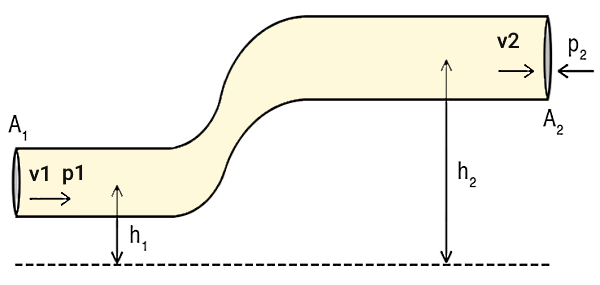
- : سطح مقطع لوله در دو نقطه ۱ و ۲
- : فشار در دو نقطه ۱ و ۲
- : سرعت در دو نقطه ۱ و ۲
- : عمق در دو نقطه ۱ و ۲
برای حل مسائل اغلب از این شکل معادله برنولی استفاده میشود.
کاربردهای معادله برنولی
همانطور که اشاره شد، معادله برنولی برای سیالات تراکمناپذیر کاربرد دارد و دامنه وسیعی از کاربردهای واقعی را شامل میشود. برای مثال، یکی از کاربردهای عملی آن لوله ونتوری یا دبیسنج ونتوری است، ابزاری که برای اندازهگیری دبی جریان مایعات در لولهها با دقت بالا استفاده میشود. این لوله به گونهای ساخته میشود که در بخشی از سطح داخلی خود تنگشدگی دارد و قطر خروجی و ورودی آن با هم برابراند، اما کاهش سطح مقطع در مسیر جریان باعث ایجاد اختلاف فشار و سرعت میشود.
همچنین معادله برنولی در طراحی توربینهای بادی نیز بکار میرود. این معادله برای بررسی جریان هوا در دو طرف توربین مفید است، زیرا سرعت هوا را به اختلاف فشار در دو طرف توربین مرتبط میکند. این ویژگی امکان تحلیل عملکرد توربین و محاسبه میزان توان تولیدی آن را فراهم میسازد.
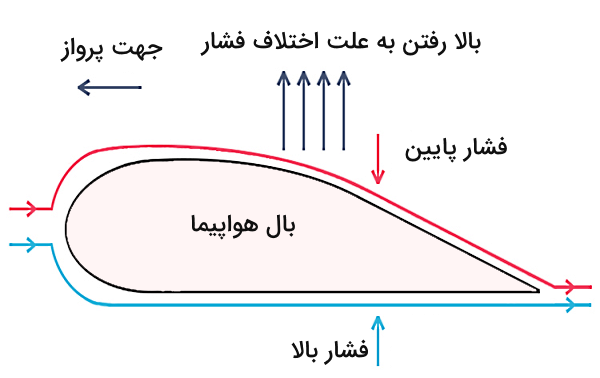
در هوانوردی نیز از معادله برنولی برای محاسبه نیروی برا (بالابرنده یا Lift) وارد بر بال هواپیما در هنگام پرواز استفاده میشود. بالهای هواپیما سطح بالایی بزرگتر و سطح پایینی کوچکتری دارند. در نتیجه هوایی که از سطح بالایی عبور میکند، باید مسیر طولانیتری را نسبت به هوای سطح پایینی طی کند. پس سرعت آن بیشتر میشود. در نتیجه فشار در بالای بال کاهش یافته و در زیر آن افزایش مییابد. این اختلاف فشار نیروی برا را ایجاد میکند که یکی از نیروهای اصلی در پرواز است. البته در این کاربرد، معادله برنولی برای نوع دیگری از سیالات یعنی هوا توضیح داده شد.
حل مثال و تمرین از فرمول فشار مایعات
در بخشهای قبل با انواع فرمول فشار مایعات کاملا آشنا شدیم. در این بخش قصد داریم با حل چند نمونه سوال تشریحی و تستی، کاربرد این فرمولها و مفاهیم را در حل سوالات مختلف تمرین کنیم.
مثال ۱
فشاری که توسط یک ستون آب با ارتفاع به سطح زیر آن وارد میشود، چقدر است؟ (چگالی آب را و شتاب جاذبه زمین را فرض کنید)
پاسخ
فشار ناشی از یک ستون آب همان فشار ناشی از نیروی وزن آن است که با سادهسازی به فرمول زیر میرسد:
مثال ۲
از یک دستگاه هیدرولیکی برای بلند کردن یک خودروی در تعمیرگاه استفاده میشود. اگر خودرو روی پیستونی با سطح مقطع قرار داشته باشد و نیرو روی پیستون کوچکتری با سطح مقطع وارد شود، کمترین نیروی لازم برای بلند کردن خودرو چقدر است؟ (شتاب جاذبه زمین را فرض کنید)
پاسخ
دقت کنید برای اینکه بتوانیم خودرو را توسط این سیستم هیدولیکی که همان جک هیدرولیکی است، بلند کنیم، لازم است بر وزن آن غلبه کنیم. در واقع اگر نیرویی که توسط این سیستم تولید میشود، از وزن خودرو کمی بیشتر باشد، خودرو بالا خواهد رفت. پس ابتدا وزن خودرو را با ضرب کردن جرم آن در شتاب جاذبه محاسبه میکنیم:
اگر تصویر بخش جک هیدرولیکی را به خاظر داشته باشید، در این سوال نیروی وزن خودرو معادل حداقل نیروی است. پس سطح مقطع بزرگتر یعنی در این سوال همان و سطح مقطع کوچکتر یا نیز همان است. به این ترتیب با مساوی قرار دادن فشارهای وارد بر این دو پیستون، نیروی اولیه که همان است، به شکل زیر به دست میآید:
بنابراین برای بلند کردن خودرویی با جرم لازم است حداقل نیرویی برابر با اعمال شود.
مثال ۳
فرض کنید شش جسم مختلف در داخل مایعی به شکل زیر قرار گرفتهاند. با این فرض که هیچکدام از این اجسام حرکتی ندارد، آنها را به ترتیب از کمترین چگالی تا بیشترین چگالی مرتب کنید:
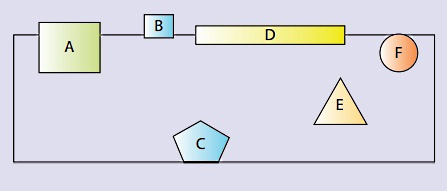
پاسخ
با توجه به قوانین شناوری، هرچه بخش بیشتری از حجم یک جسم بالاتر از سطح آب قرار داشته باشد، چگالی آن کمتر و دارای شناوری مثبت است. بنابراین جسم B باید کمترین چگالی را داشته باشد، سپس به ترتیب اجسام A ،D و F قرار میگیرند. جسم E در مرحله بعد قرار دارد، چون بهطور خنثی شناور است و در واقع چگالی آن با چگالی مایع برابر است. جسم C دارای شناوری منفی است، چون چگالی آن بیشتر از چگالی مایع است. بنابراین ترتیب چگالی اجسام از کم به زیاد به صورت زیر است:
مثال ۴
مانومتری را در نظر بگیرید که از مایعی با چگالی تا ارتفاع پر شده است. اگر مایع دیگری با چگالی از بازوی سمت راست مانومتر داخل آن ریخته شود، طوری که بدون مخلوط شدن روی مایع اول قرار بگیرد، با در نظر گرفتن نشان دهید از برابری فشار مطلق در دو نقطه میتوان نتیجه گرفت .
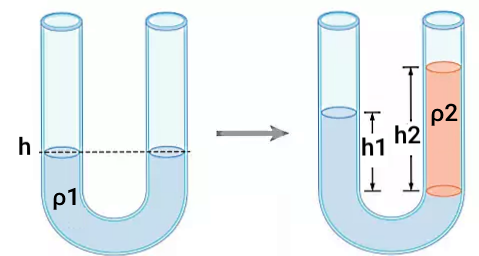
پاسخ
پس از اینکه مایع دوم روی مایع اول ریخته میشود، سطح مایع اول در بازوی راست لوله U شکل پایین میرود و در سمت مقابل نسبت به حالت اول بالاتر قرار میگیرد. برای اینکه بتوانیم از اصل برابری فشار دو نقطه از یک مایع در عمق برابر استفاده کنیم، لازم است دو نقطهای که انتخاب میکنیم کاملا داخل یک مایع قرار داشته باشند. برای مثال نقطه A را در بازوی راست و در ابتدای ستون مایع با چگالی در نظر میگیریم (نقطه A داخل مایع دوم نیست).
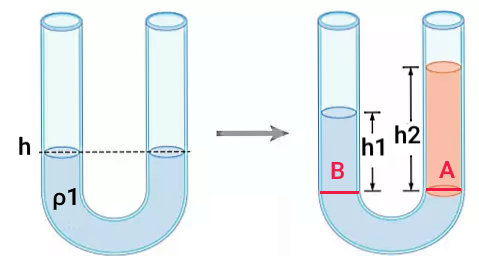
حالا اگر نقطه B را در بازوی چپ و در همین سطح انتخاب کنیم، هر دو نقطه کاملا داخل مایع اول قرار دارند. به این ترتیب فشار وارد بر نقطه A یا مجموع فشار ناشی از ستون مایع با چگالی و فشار اتمسفری است که از دهانه باز لوله به سطح این مایع وارد میشود:
اگر به رابطه بالا خوب دقت کنید، در واقع همان فرمول فشار مطلق برای نقطه A نوشته شده است که در آن برابر است با فشار پیمانهای و هم که فشار اتمسفر است. حالا میرویم سراغ فشار وارد بر نقطه B یا که برابر است با مجموع فشار ناشی از وزن ستون مایع اول با ارتفاع و فشار هوایی که از دهانه باز لوله به سطح این مایع اعمال میشود:
این رابطه هم همان فرمول فشار مطلق وارد شده به نقطه B است. پس اصل برابری فشار در دو نقطه از یک مایع با عمق یکسان به برابری فشار مطلق در این دو نقطه تبدیل شد. با برابر قرار دادن این دو فشار داریم:
فشار اتمسفر در دو طرف این تساوی یکی است و حذف میشود. پس از سادهسازی داریم:
مثال ۵
دو سرنگ به شکل زیر به هم متصل شدهاند. اگر یک نیروی به پیستون سرنگ وارد شود، فشاری که توسط این پیستون به روغن داخل شلنگ منتقل میشود، چقدر است؟ همچنین نیروی لازم برای ممانعت از به سمت بیرون رفتن پیستون سرنگ را محاسبه کنید:
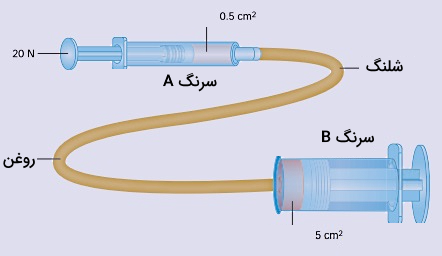
پاسخ
فشاری که توسط نیروی به پیستون سرنگ وارد میشود، با استفاده از مقطع این پیستون و به شکل زیر حساب میشود:
این فشار بنا بر اصل پاسکال بدون کم و زیاد شدن از طریق روغن داخل شلنگ به پیستون سرنگ منتقل میشود. پس نیرویی که این فشار روی پیستون این سرنگ وارد میکند، برابر خواهد شد با:
مثال ۶
مقداری آب با چگالی در یک لوله افقی جریان دارد. فرض کنید سطح مقطع لوله در محل کاهنده از به کاهش یابد، فشار استاتیک قبل از کاهنده و سرعت جریان باشد. همچنین جریان آب را تراکمناپذیر و بدون اصطکاک در نظر بگیرید. در این صورت فشار استاتیک پس از محل کاهنده چقدر اندازهگیری میشود (شتاب جاذبه زمین را فرض کنید)؟
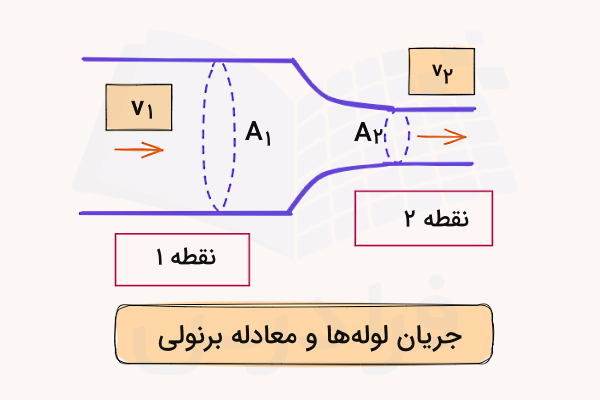
پاسخ
با مشخص کردن دو نقطه ۱ (قبل کاهش سطح مقطع) و ۲ (بعد از کاهش سطح مقطع) در لوله، معادله برنولی را به شکل زیر مینویسیم:
اما پیش از عددگذاری بهتر است معادله بالا را سادهتر کنیم تا محاسبات راحتتر انجام شود. برای مثال، چون طبق صورت سوال ارتفاع در نقطه ۲ نسبت به نقطه ۱ تغییری نمیکند، پس دو جمله و با هم برابر هستند () و از طرفین حذف میشوند:
با توجه به اینکه دنبال مقدار فشار پس از محل کاهنده یعنی هستیم، پس با بردن آن به یک سمت تساوی خواهیم داشت:
اما برای به دست آوردن پاسخ در این معادله علاوه بر ، نیز مجهول است. تعیین سرعت در نقطه ۲ با استفاده از معادله پیوستگی و به شکل زیر امکانپذیر است:
پیش از عددگذاری لازم است مقادیر داده شده را بر حسب واحدهای SI بنویسیم. برای مثال، تبدیل بار به پاسکال را داریم که به شکل زیر انجام میشود:
همچنین برای مقادیر سطح مقطع داریم:
بنابراین پاسخ به شکل زیر است:
تمرین ۱
تمرین ۲
تمرین ۳
تمرین ۴
تفاوت فشار در مایعات و گازها
هر حالتی از ماده که توانایی جاری شدن یا جریان یافتن داشته باشد، شاره یا سیال نامیده میشود. بنابراین مایعات و گازها شاره محسوب میشوند. شارهها وزن دارند و در نتیجه فشار وارد میکنند. هنگامی که یک شاره در یک ظرف قرار میگیرد، فشار شاره در همه جهات و در تمام نقاط شاره اعمال میشود. از آنجا که مولکولهای یک شاره همواره در حرکت سریع و مداوم هستند، ذرات بهطور یکسان در هر جهتی حرکت میکنند. همین مسئله موجب میشود فشاری که توسط یک شاره وارد میشود، از همه جهات بر یک جسم اثر کند.
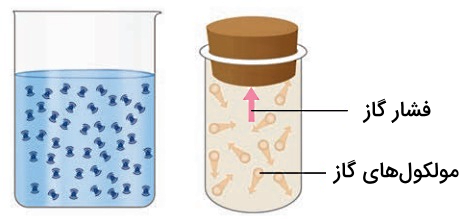
فرمول اولیه فشار در شارهها همان فرمول اصلی فشار یعنی است. این فرمول در مورد مایعات به شکلی که در بخشهای ابتدایی توضیح دادیم، به فرمولهایی مانند و کاهش مییابد. اما در مورد گازها بهویژه گازهای ایدهآل لازم است به این نکته توجه کنیم که فشار به عوامل دیگری مانند دما، حجم و مقدار گاز بستگی دارد.
این وابستگی طبق قانون گازها به شکل زیر تعریف میشود:
- : فشار گاز ایدهآل بر حسب پاسکال ()
- : حجم گاز بر حسب متر مکعب ()
- : مقدار گاز بر حسب مول ()
- : ثابت جهانی گازها با مقدار عددی
- : دمای گاز بر حسب کلوین ()
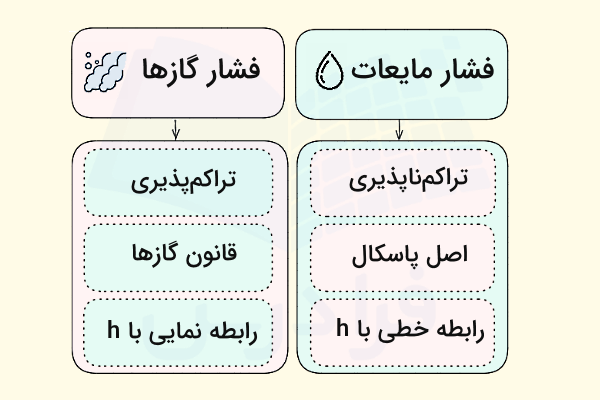
بهطور کلی تفاوت فشار در مایعات و گازها در فاکتورهایی مانند تراکمپذیری، وابستگی فشار به عمق، نحوه انتقال فشار و مقدار فشار خلاصه میشود. برای مثال، چون مایعات تقریبا تراکمناپذیراند، با افزایش فشار حجم آنها تغییر محسوسی پیدا نمیکند. بنابراین فشار در مایعات طبق اصل پاسکال بهطور یکنواخت در تمام نقاط مایع منتقل میشود. اما گازها به شدت تراکمپذیراند، به این مفهوم که با تغییر فشار حجم آنها نیز طبق قانون بویل تغییر زیادی میکند.
همچینن در مایعات فشار به عمق بستگی دارد. بنابراین در یک مایع ساکن، فشار در هر نقطه فقط به ارتفاع ستون مایع بالای آن نقطه وابسته است. اما در گازها به علت تراکمپذیری، رابطه فشار با عمق یا ارتفاع پیچیدهتر است. برای نمونه، در جو زمین فشار با افزایش ارتفاع به شکل نمایی کاهش پیدا میکند (قانون بارومتریک).
به علاوه نحوه انتقال فشار در مایعات در تمام جهات و به شکلی یکسان است (طبق اصل پاسکال)، در حالی که در مورد گازها باز هم به دلیل تراکمپذیری، تغییرات دما و حجم روی انتقال فشار موثر هستند. در نهایت مقدار فشار مایعات اغلب همان فشار ناشی از وزن خود مایع و فشار خارجی (مثل فشار هوا) است، در حالی که فشار گازها همان فشار ناشی از برخورد مداوم مولکولهای گاز با دیواره ظرف است.
کاربردهای فرمول فشار مایعات
تا اینجا با انواع فرمول فشار مایعات آشنا شدیم. این فرمولها کاربردهای گستردهای در بخشهای مختلف صنعت، سلامت، سدسازی، طراحی مخازن و ... دارند. در ادامه به برخی از این کاربردها اشاره کردهایم:
- هیدرولیک و نیروی بالابری: کاربرد در سیستمهای هیدرولیک ماشینآلات سنگین، تحلیل جکهای هیدرولیکی و پرسهای صنعتی
- فشار در زیر آب: کاربرد در حوزه غواصی و سازههای زیردریایی، بررسی تاثیر عمق بر فشار وارد بر بدن غواص، طراحی زیردریاییها و استحکام آنها در برابر فشار
- مهندسی عمران: طراحی سدها و مخازن آب، نحوه محاسبه فشار وارد بر دیوارههای یک سد، اهمیت درک فشار برای طراحی ایمن سازهها
- فشار مایعات در بدن انسان: مکانیسم تنظیم فشار خون در بدن
- فشار در گیاهان: تحلیل نحوه انتقال آب از ریشه به برگ، نقش فشار اسمزی و فشار تورگور در گیاهان
یادگیری فیزیک پایه با فرادرس
فشار در مایعات یکی از مهمترین مباحثی است که در کتابهای فیزیک پایه ۳ یا فیزیک عمومی به آن پرداخته میشود. البته مباحث فیزیک پایه ۱ مقدمهای برای یادگیری بهتر مفاهیم این کتاب محسوب میشوند. به همین علت در این بخش مجموعهای از فیلمهای آموزشی فرادرس در زمینه فیزیک پایه دانشگاهی را معرفی میکنیم:
آزمون فشار مایعات
در انتهای این مطلب از مجله فرادرس بهعنوان یک جمعبندی تمام فرمولهای مربوط به فشار در مایعات را در جدول زیر خلاصه کردهایم:
| انواع فرمول فشار مایعات | |
| فشار مایعات ساکن | |
| فشار مایعات متحرک | |
| اصل پاسکال در جک هیدرولیکی | |
| نیروی شناوری | |
| معادله برنولی برای دو نقطه | |
| معادله پیوستگی برای دو نقطه | |
همچنین در ادامه میتوانید با حل ده سوال چهار گزینهای، میزان یادگیری خود را در مبحث فرمول فشار مایعات بسنجید. پس از پاسخدهی با کلیک روی گزینه «دریافت نتیجه آزمون» نمره نهایی شما قابل مشاهده است.












