شار الکتریکی – به زبان ساده
در این مقاله در نظر داریم تا با زبانی ساده، به تشریح یکی از مهمترین مفاهیم فیزیک الکترومغناطیس، یعنی شار الکتریکی (Electric Flux) بپردازیم.
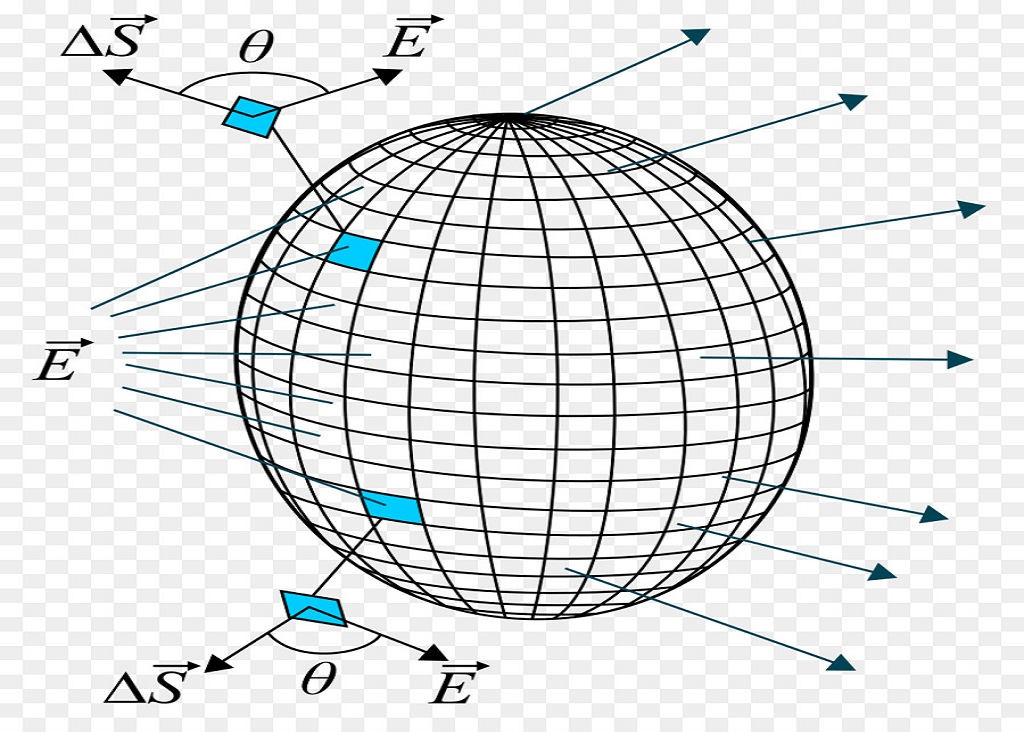
به بیانی ساده، شار الکتریکی معیاری از میزان توزیع میدان الکتریکی در یک سطح معین است. مفهوم شار الکتریکی اساس کار قانون مهم و کاربردی گاوس (Gauss's law) است که جهت محاسبه میدان الکتریکی ساختارهای متقارن از آن استفاده میکنند. در ادامه این مطلب با ما همراه باشید.
شار الکتریکی
همانطور که در مقدمه مقاله اشاره کردیم، توسط پارامتر شار الکتریکی که آن را غالباً با نماد Φ نشان میدهند، میتوان به مقدار یا توزیع میدان الکتریکی در ناحیهای از فضا پی برد. از مباحث فیزیک پایه میدانید که میدان الکتریکی اطراف توزیع بار را به صورت کیفی، با خطوطی به شکل زیر نمایش میدهند.
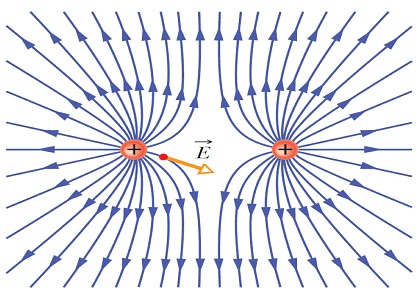
پس به عبارت دیگر، شار الکتریکی را میتوان میزان خطوط میدان عبوری از یک سطح در نظر گرفت. البته بهتر است که عبارت شار الکتریکی کل را برای تعریف فوق انتخاب کرد. در فیزیک الکترومغناطیس، غالباً در محاسبات با شار الکتریکی خالص سروکار دارند که میزان خطوط عبوری میدان الکتریکی از یک سطح بسته تعریف میشود. در مورد چرایی سطح بسته، در ادامه مقاله توضیحاتی ارائه خواهد شد. لازم به ذکر است که این سطح بسته به سطح گاوسی نیز موسوم است.
از آنجایی که میدان الکتریکی کمیتی برداری است، مقدار خطوط عبوری از یک سطح را که همان تعریف شار الکتریکی است، به صورت حاصل ضرب نقطهای (ضرب داخلی) بردار میدان الکتریکی () در بردار عمود بر سطح () تعریف میکنند. یعنی:
(1)
عبارت فوق یک عبارت کلی جهت سنجش میزان شار عبوری از یک سطح است. به عبارت دیگر، جهت محاسبه دقیق شار الکتریکی گذرنده از یک سطح، ما باید به محاسبه حاصل ضرب نقطهای بردار میدان الکتریکی () و بردار عمود بر سطح () در جزءهای کوچک پرداخته و در نهایت مجموع آنها را حساب کنیم.
دلیل این امر این است که زاویه بردار میدان الکتریکی () با بردار عمود بر سطح () در همهجای سطح یکسان نیست. پس عبارت (۱) را میتوانیم به صورت جمع (انتگرال) تمامی خطوط میدان گذرنده از سطح کوچک بنویسیم:
(2)
محاسبه شار الکتریکی
جهت محاسبه شار الکتریکی، قدم اول نوشتن فرمول یا رابطهای است که میخواهیم از آن استفاده کنیم. دو رابطه (1) و (2) را همیشه به یاد داشته باشید.
همانطور که در بخش قبل دیدیم، شار الکتریکی گذرنده از یک سطح برابر با حاصل ضرب نقطهای بردار میدان الکتریکی () در بردار عمود بر آن سطح () است. قدم دوم تعیین اندازه بردار میدان الکتریکی، جهت محاسبه ضرب نقطهای است. معمولاً در مسائل مقدار میدان الکتریکی جزو معلومات است. قدم سوم نیز تعیین اندازه بردار عمود بر سطح () و تعیین زاویه آن با بردار میدان الکتریکی () است. توجه داشته باشید که بردار سطح همیشه بر سطح عمود و به سمت خارج از آن است. همچنین منظور از اندازه بردار عمود بر سطح، همان مساحت سطحی است که خطوط میدان الکتریکی از آن عبور میکنند.
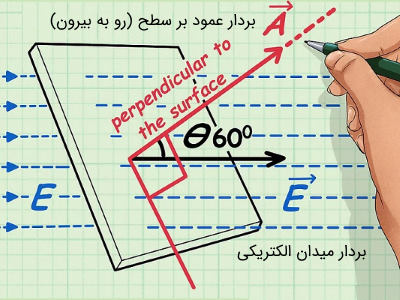
به طور مثال، زاویه بین دو بردار مذکور در شکل فوق، 60 درجه است. با فرض اینکه مساحت سطح مذکور ۵ متر مربع و اندازه میدان 500 نیوتن بر کولن باشد، شار الکتریکی گذرنده از سطح مذکور با واحد سنجش () به صورت زیر است:
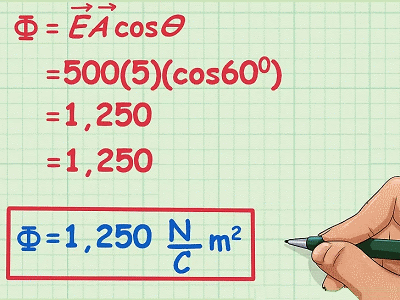
در حالت فوق، فرض کردیم که میدان الکتریکی در فضا وجود داشت. در واقع منشأ میدان الکتریکی مشخص نبود و تنها شار الکتریکی گذرنده از یک سطح محاسبه شد. در ادامه فرض میکنیم که منشأ میدان توزیع بار باشد. در این حالت ما شار الکتریکی گذرنده از یک سطح بسته را محاسبه میکنیم. سطح بسته بدین منظور در نظر گرفته میشود که شار الکتریکی خالص محاسبه شود. در این حالت تفاوتی در رابطه (2) ایجاد نشده و تنها انتگرال روی سطح بسته محاسبه میشود. در واقع در اینجا مساحت سطح بسته گاوسی است.
(3)
با توجه به مطالب گفته شده در فوق، یک سطح بسته (موسوم به سطح گاوسی) را متناسب با توزیع بار رسم میکنیم. به طور مثال یک بار نقطهای یا توزیع کروی بار نیاز به سطح گاوسی کروی و یک توزیع خطی بار نیاز به سطح گاوسی استوانهای دارد.
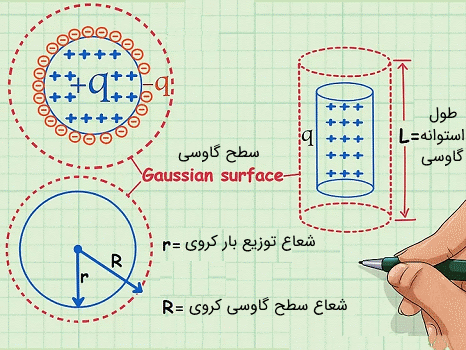
در این حالت مشاهده میشود که زاویه بردار میدان الکتریکی () با بردار عمود بر سطح () یا همان جز دیفرانسیلی سطح، صفر درجه است. از آنجایی که میدان الکتریکی وابستگی به جزء دیفرانسیلی سطح ندارد از انتگرال بیرون آمده و حاصل انتگرال که به معنی جمع تمامی جزءهای دیفرانسیلی سطح است، برابر با مساحت سطح گاوسی میشود. به عبارت دیگر به رابطه ساده رسیدیم. توجه داشته باشید که در اینجا خطوط میدان الکتریکی که از سطح گاوسی عبور میکند، در همه جا یکسان و برابر است (چگالی خطوط ثابت است).
محاسبه شار الکتریکی از قانون گاوس
اساس و مبنای کار قانون گاوس ارتباط تنگاتنگی با شار الکتریکی گذرنده از سطح بسته دارد. قانون گاوس به شکل ساده زیر است:
(4)
نکته مهمی که به هنگام استفاده از قانون گاوس باید به آن توجه کنیم، تعیین صحیح مقدار است. خطوط میدان الکتریکی گذرنده از یک سطح بسته، متناسب با مقدار بار است که توسط سطح بسته (سطح گاوسی) محصور شده است. پس به یاد داشته باشید که در قانون گاوس مقدار بار محصور شده توسط سطح گاوسی است.
برای روشنتر شدن این مطلب، یک توزیع کروی بار را در نظر بگیرید. یک بار سطح گاوسی را بیرون توزیع بار رسم میکنیم. در این صورت مقدار برابر با مقدار کل بار توزیع کروی است. حال فرض کنید که سطح گاوسی را این بار دورن توزیع بار رسم میکنیم. در این حالت آیا شار وارد شده به سطح گاوسی برابر با حالت قبل است؟ واضح است که پاسخ منفی است، چرا که مقدار بار کمتری توسط سطح گاوسی محصور شده است.
جهت محاسبه بار الکتریکی محصور شده توسط سطح گاوسی میتوان از چگالی بار متناسب با توزیع بار استفاده کرد. چگالیهای مختلف بار در زیر آمدهاند:
(5)
(6)
(7)
پس مطابق با قانون گاوس، شار الکتریکی گذرنده از سطح بسته گاوسی به صورت زیر است:
(8)
واحد سنجش نفوذ پذیری الکتریکی، است که با توجه به رابطه فوق، واحد سنجش شار الکتریکی نیز نتیجه میشود.
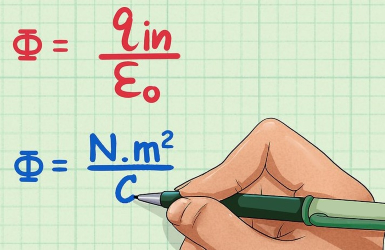
مثال
یک سطح گاوسی استوانهای شکل، مطابق با شکل زیر در نظر بگیرید. سطح مذکور در میدان الکتریکی یکنواخت قرار دارد. شار الکتریکی گذرنده از این سطح بسته چقدر است؟
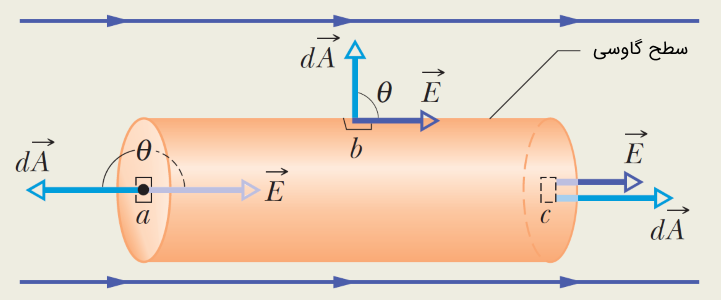
با توجه به سطح بسته فوق، جهت محاسبه شار الکتریکی از رابطه زیر استفاده میکنیم.
(9)
در اینجا سه بردار عمود بر سطح وجود دارد. یکی روی بدنه استوانه و دوتای دیگر روی دو قاعده که در شکل نشان داده شده است. همانطور که در متن مقاله نیز اشاره کردیم و در فرمول فوق هم مشخص است، باید ضرب نقطهای بردار میدان الکتریکی و بردار عمود بر سطح را به دست آوریم. با توجه به زوایای درون شکل داریم:
(10)
با توجه به شکل، حاصل انتگرال به دلیل زاویه ۹۰ درجه بین دو بردار و صفر است. همچنین در انتگرال زاویه بین دو بردار مذکور 180 درجه و در انتگرال زاویه بین دو بردار 0 درجه است. در نتیجه این دو مقدار یکدیگر را خنثی میکنند.
(11)
با توجه به مطلب فوق، نتیجه میشود که شار الکتریکی خالص که به معنی خطوط میدان الکتریکی گذرنده از یک سطح بسته است، به این دلیل که تمام خطوط میدان وارد شده از چپ از سمت راست نیز خارج میشود (بدون تغییر)، صفر است. توجه داشته باشید که در اینجا میدان الکتریکی در همهجای فضا یکنواخت (Uniform) است.
به یاد داشته باشید که هرگاه سطح گاوسی بسته داشته باشیم، شار الکتریکی خالص در صورتی صفر است که میدان الکتریکی در فضا وجود داشته باشد و ما سطحی همانند مثال فوق را در میدان قرار دهیم. اما در قانون گاوس که بیشتر به منظور محاسبه میدان الکتریکی ناشی از توزیعهای مختلف بار به کار میرود، با اینکه سطح بستهای را به دور توزیع بار در نظر میگیریم اما شار خالص صفر نیست. برای روشن شدن این مطلب به شکل زیر دقت کنید:
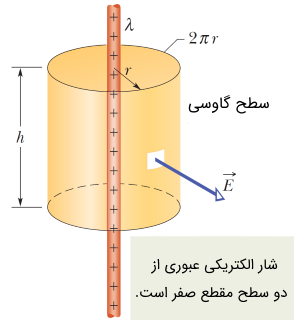
در شکل فوق، خطوط میدان الکتریکی با هر جزء دیفرانسیلی زاویه صفر درجه ساخته و از سطح گاوسی بسته خارج میشوند. در حالی که در شکل (7) خطوط میدان یکنواخت از یک سمت وارد و از سمت دیگر خارج میشوند.
مثال
مکعبی به ضلع ۲ سانتیمتر را در نظر بگیرید که مطابق با شکل (9) در یک میدان الکتریکی غیر یکنواخت (Nonuniform) قرار دارد. توزیع میدان غیر یکنواخت مذکور به صورت زیر است:
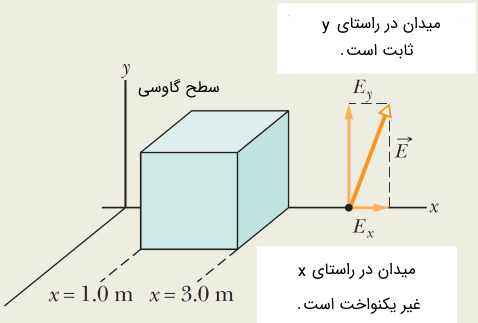
در اینجا قصد داریم تا شار الکتریکی گذرنده از وجه سمت راست، سمت چپ و بالا را محاسبه کنیم. با توجه به توزیع میدان الکتریکی، مشاهده میشود که تنها در راستای محور توزیع غیر یکنواخت میدان الکتریکی داریم و در راستای میدان الکتریکی ثابت است.
از آنجایی که میدان الکتریکی در راستای مقدار ثابت 4 را دارد، شار الکتریکی گذرنده از وجه فوقانی مکعب به صورت زیر محاسبه میشود. توجه داشته باشید که در اینجا از رابطه کلی استفاده میکنیم. در نتیجه:
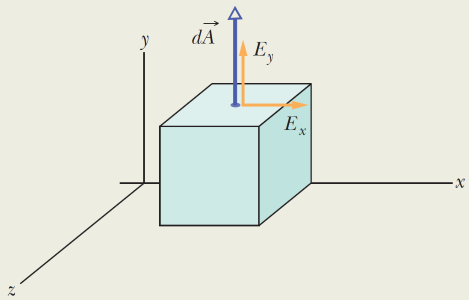
لازم به ذکر است که شار الکتریکی گذرنده از وجه پایینی نیز همین مقدار تنها با یک علامت منفی است. چرا که زاویه بین دو بردار و به اندازه 180 درجه است که است. همچنین در راستای اگر سطح مکعبی را بسته فرض کنیم، شار الکتریکی خالص صفر است. چرا که خطوط یکنواخت میدان از وجه پایینی وارد و از وجه فوقانی خارج میشوند.
حال به محاسبه شار الکتریکی گذرنده از وجه سمت راست مکعب مذکور میپردازیم. از آنجایی که میدان الکتریکی با بردار عمود بر سطح وجه راست زاویه ۹۰ درجه میسازد ()، مولفه میدان الکتریکی سهمی در شار الکتریکی گذرنده از وجه سمت راست ندارد. همانطور که میدانید حاصل ضرب نقطهای بردارهای یکه و صفر است. با توجه به مطالب گفته شده داریم:
توجه داشته باشید که در اینجا مختصه مکانی است که میدان الکتریکی با آن تغییر میکند. مختصه مکانی ار مبدأ مختصات سنجیده شده و در وجه سمت راست مکعب مقدارش است. دقت داشته باشید که را در اینجا با طول ضلع مکعب اشتباه نگیرید. بدیهی است که انتگرال جزء دیفرانسیلی سطح نیز مساحت وجه سمت راست مکعب است.
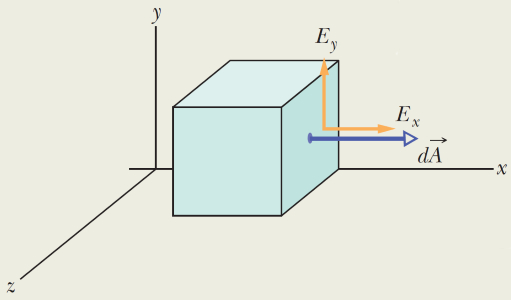
جهت محاسبه شار الکتریکی گذرنده از وجه سمت چپ نیز روند مشابه فوق را طی میکنیم. در اینجا نیز مولفه میدان الکتریکی سهمی در شار الکتریکی ندارد و تنها مقدار متفاوت با حالت قبل بوده و برابر با ۱ است (فاصله از مبدأ مختصات). در نتیجه شار الکتریکی گذرنده از وجه سمت چپ برابر با میشود.
همچنین شار الکتریکی گذرنده از دو وجهی که در راستای محور قرار دارد، صفر است. چرا که میدان الکتریکی مذکور هیچ مولفهای در راستای ندارد. با توجه به مطالب گفته شده در این مقاله، اگر مکعب را سطحی بسته فرض کنیم، آیا شار الکتریکی خالص آن همانند مثال قبل صفر است؟ به دلیل غیر یکنواخت بودن میدان الکتریکی پاسخ این سوال منفی است. چرا که مقدار شار وارد شده از یک وجه، با شار خارج شده از وجه دیگر (در راستای )، به دلیل غیر یکنواخت بودن میدان الکتریکی متفاوت است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش فیزیک پایه ۲
- مجموعه آموزشهای دروس مهندسی برق
- آموزش الکترومغناطیس ۱
- امواج رادیویی -- به زبان ساده
- امپدانس و محاسبه آن -- به زبان ساده
- خازن در جریان متناوب -- به زبان ساده
^^













تشکر خداقوت