حسابان کسری — به زبان ساده
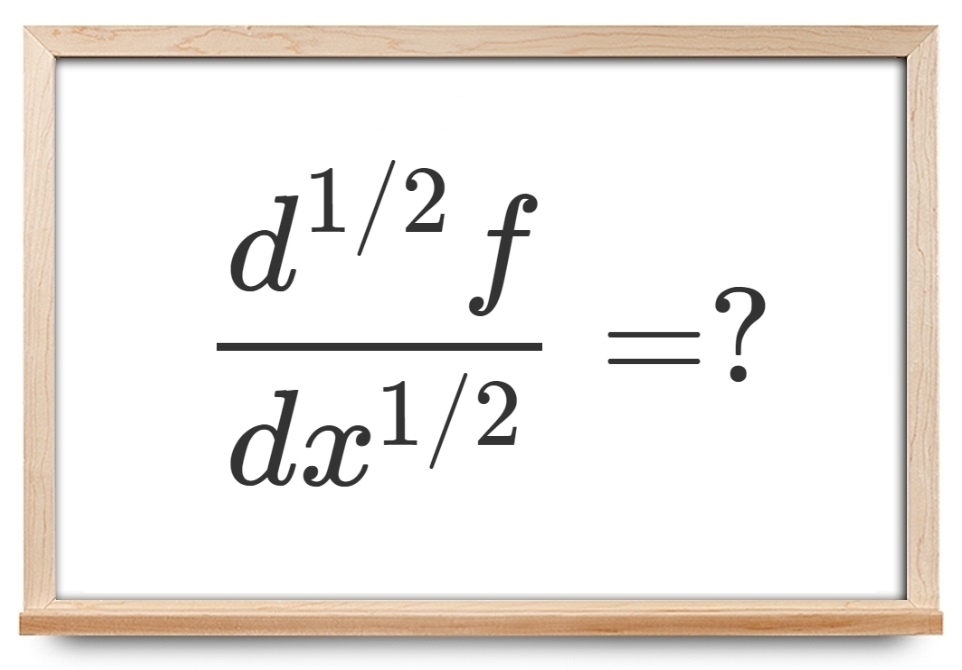
حساب دیفرانسیل به طور مستقل توسط «سر آیزاک نیوتن» (Sir Isaac Newton) و «گوتفرید ویلهلم لایبنیتس» (Gottfried Wilhelm Leibniz) اختراع شد و چنین شد که مفهوم مشتق مرتبه $$n$$اُم، یعنی اعمال $$ n $$ بار پیاپی عملیات مشتقگیری، معنیدار بود. در سال 1695، هوپیتال در نامهای خطاب به لایبنیتس این پرسش را مطرح کرد که آیا $$n$$ میتواند عددی غیر از یک عدد صحیح، مانند $$ n = 1 / 2 $$ باشد. لایبنیتس پاسخ داد كه «این موضوع به تناقض منتهی میشود كه در آینده نتایج مفیدی از آن حاصل میشود.» پاسخ لایبنیتس صحیح بود، اما تنها چند قرن طول کشید مشخص شود که گفته او صحیح بوده است. در این آموزش، به این پرسش پاسخ میدهیم که مثلاً مشتق مرتبه $$ 1 / 2 $$ چیست و بنابراین نظریه «حسابان کسری» (Fractional Calculus) را معرفی خواهیم کرد.
بررسی شهودی حسابان کسری
دو راه برای تفسیر عبارت زیر وجود دارد:
$$ \large \frac { d ^ n f } { d t ^ n } $$
راه اول همانی است که در حسابان پایه آموختهایم: عبارت بالا تابعی است که از $$ n$$ با مشتقگیری $$ f $$ نسبت به $$ t $$ به دست آمده است. راه دوم زیرکانهتر است: این عبارت را به عنوان یک اپراتور یا عملگر در نظر میگیریم که روی تابع $$ f ( t) $$ عمل میکند و با پارامتر $$ n $$ مشخص میشود. آنچه هوپیتال پرسید همان رفتار این عملگر عمومی بود، با این فرض که $$ n $$ یک عدد صحیح نباشد.
طبیعیترین روش برای پاسخ به این پرسش در نظر گرفتن مشتقگیری و انتگرالگیری به عنوان تبدیلهایی است $$ f $$ را میگیرند و یک تابع جدید نتیجه خواهند داد. بنابراین، ما به دنبال عملگری هستیم که به طور مداوم $$ f $$ را به مشتق یا پادمشتق مرتبه $$ n$$ تبدیل کند.
انتگرال و مشتق مرتبه کسری
نقطه آغاز فهم عملگرهای دیفرانسیل و انتگرال مرتبه کسری، فرمولی به نام فرمول کوشی برای انتگرال مکرر است. اگر پادمشتق مرتبه $$ n$$ یک تابع را محاسبه کنیم، خواهیم داشت:
$$ \large I ^ n f ( t ) = \frac { 1 } { ( n - 1 ) ! } \int _ { 0 } ^ { t } ( t - \tau ) ^ { n - 1 } f ( \tau ) d \tau $$
تعمیم تابع کسری تابع گاما است. اگر تساوی $$ \Gamma ( n ) = ( n - 1 )! $$ را در نظر بگیریم، آنگاه یک راه واضح برای تعمیم فرمول کوشی برای در نظر گرفتن مرتبه حقیقی $$ \alpha $$ (اکیداً بزرگتر از صفر)، به صورت زیر است:
$$ \large I ^ \alpha f ( t ) = \frac { 1 } { \Gamma ( \alpha ) } \int _ { 0 } ^ { t } ( t - \tau ) ^ { \alpha - 1 } f ( \tau ) d \tau $$
و در واقع، این یک عملگر معتبر برای انتگرالگیری مرتبه کسری است. این عبارت، «انتگرال ریمان-لیوویل» (Riemann-Liouville Integral) نامیده میشود. در ادامه در مورد مقدماتی «چپ» بحث خواهیم کرد. در حقیقت بسیاری از عملگرهای انتگرالگیری مرتبه کسری وجود دارند که در این زمینه پذیرفته شدهاند، اما انتگرال ریمان-لیوویل یا R-L سادهترین عملگر برای استفاده و درک است. توجه کنید که $$\alpha$$ میتواند یک عدد مختلط با بخش حقیقی اکیداً بزرگتر از صفر نیز باشد، اما برای سادگی فرض خواهیم کرد که $$\alpha$$ حقیقی است. مورد خاص $$ \alpha = 1 / 2 $$ «شبهانتگرال» (Semi-Integral) نامیده میشود.
انتگرالگیری R-L از روابط مهم زیر پیروی میکند:
$$ \large \begin {aligned}
I ^ { \alpha } \left ( I ^ { \beta } f \right ) & = I ^ { \alpha + \beta } f \\
\frac { d } { d x } I ^ { \alpha + 1 } f & = I ^ { \alpha } f
\end {aligned} $$
شاید بگویید که میتوانیم مشتق مرتبه $$ \alpha $$ را به صورت زیر بنویسیم:
$$ \large D ^ {\alpha} = I ^ { - \alpha} $$
البته که چنین کاری صحیح نیست. مشکل (یکی از مشکلات) این است که تابع گاما برای صفر یا اعداد صحیح منفی تعریف نشده است. این امر موجب میشود یک مشتقگیری کلی ایجاد کنیم که برای مشتق معمولی هم کار نمیکند. بنابراین، باید راهی خلاقانه برای این موضوع پیدا کنیم.
باید توجه داشت که $$ n $$ بار مشتق گرفتن پس از $$ n $$ بار انتگرالگیری معادل با عملگر همانی است:
$$ \large \frac { d ^ { n } } { d t ^ { n } } \left ( I ^ { n } f ( t ) \right ) = f ( t ) $$
این بدین معنی است که مشتق همان وارون سمت چپ انتگرال است. البته انتگرالگیری وارون چپ مشتق نیست، زیرا انتگرالگیری یک ثابت دلخواه اضافه میکند. بنابراین، عبارت زیر همیشه صحیح نیست:
$$ \large I ^ n \left ( \frac { d ^ n } { d t ^ { n } } f ( t ) \right ) = f ( t ) $$
با توجه به این مشخصات، انتظار داریم مشتق مرتبه کسری $$ \alpha $$ دارای ویژگی زیر باشد:
$$ \large D ^ { \alpha } \left ( I ^ { \alpha } f ( t ) \right ) = f ( t ) $$
بدیهی است که ما علاقهمندیم بتوانیم مشتقات کسری را بر حسب عملگرهایی که درک میکنیم بنویسیم. ما مشتقگیری مرتبه صحیح را درک میکنیم و همچنین با انتگرالگیری مرتبه صحیح و مرتبه غیرصحیح آشنا هستیم. عملگری که میتوانیم از این عملگرهایی که خاصیت حذف سمت چپ را دارند، بسازیم، به صورت زیر است:
$$ \large D ^ { \alpha } f = \frac { d ^ { \lceil \alpha \rceil } } { d t ^ { \lceil \alpha \rceil } } \left ( I ^ { \lceil \alpha \rceil - \alpha } f \right ) $$
که در آن، $$\lceil \alpha \rceil $$ تابع سقف $$ \alpha $$ نامیده میشود و $$ \alpha $$ را به عدد صحیح بزرگتر از آن گرد میکند. بنابراین، عملگر مناسب به صورت زیر خواهد بود:
$$ \large D ^ { \alpha } f ( t ) = \frac { 1 } { \Gamma ( \lceil \alpha \rceil - \alpha ) } \frac { d ^ { \lceil \alpha \rceil } } { d t ^ { \lceil \alpha \rceil } } \int _ { 0 } ^ { t } ( t - \tau ) ^ { \lceil \alpha \rceil - \alpha - 1 } f ( \tau ) d \tau $$
این عبارت مشتق کسری سمت چپ ریمان-لیوویل است. با دیدن آن به وضوح میتوان فهمید که چرا تقریباً 300 سال طول کشید تا این زمینه پژوهشی به هر جایی برود: بیشتر محاسبات در حسابان کسری اگر چه دستی و بدون کمک کامپیوتر انجام میشود، اما خستهکننده است. مورد خاص $$\alpha = 1/2$$ شبهمشتق نامیده میشود.
با استفاده از انتگرال و مشتق مرتبه کسری که نوشتیم، اکنون میتوانیم آنها را به صورت تکهای ترکیب کنیم تا اپراتور دیفرنتگرال (Differintegral) را تعریف کنیم:
$$ \large J ^ { \alpha } f = \left \{ \begin {array} { l l }
D ^ { \alpha } f & \text { if } \alpha > 0 \\
f & \text { if } \alpha = 0 \\
I ^ { | \alpha | } f & \text { if } \alpha < 0
\end {array} \right . $$
تصویر متحرک زیر نشان میدهد که چگونه دیفرنتگرال ریمان-لیوویل به طور مداوم بین $$ f ( x ) = x $$، $$ f ( x ) = 1 $$ و $$ f (x ) = \frac 12 x ^ 2 $$ تبدیل میشود.
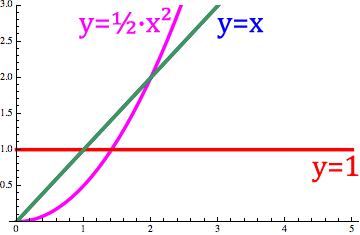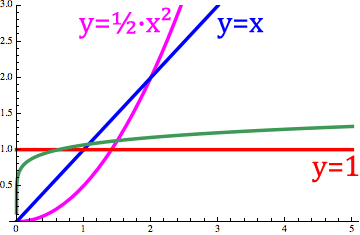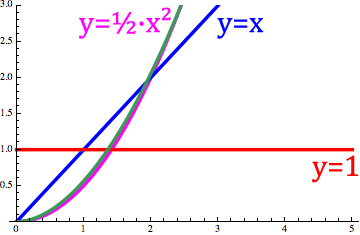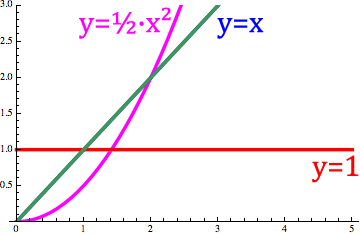
همانطور که مشاهده میکنید، با تغییر مقدار $$ \alpha $$ از $$ - 1 $$ تا $$ 1 $$، دیفرنتگرال که با منحنی سبز نشان داده شده است، بین خط $$ y = 1 $$ و $$ y = \frac 12 x ^ 2 $$ جابهجا میشود.
ویژگیهای حسابان کسری
وقتی میخواهیم ویژگیهای حسابان کسری را بنویسیم، باید بسیاری از آنچه را که از قبل میدانیم کنار بگذاریم و طبیعی و بدیهی تلقی کنیم.
بسیاری از خصوصیات اساسی مشتق و انتگرال معمولی که همه ما با آنها آشناییم و کار کردهایم، مانند قاعده زنجیرهای و قاعده ضرب، به طور کلی در مشتقات و انتگرالهای مرتبه کسری برقرار نیستند یا اینکه شکلهای پیچیدهای خواهند داشت. با این حال، انتگرال و مشتق ریمان-لیوویل که مورد بحث قرار دادیم، تنها اپراتورهای دیفرنتگرال ممکن نیستند و در حقیقت، روشهای مختلف برای تعمیم مشتقگیری و انتگرالگیری با مراتب غیرصحیح وجود دارد و انجام این کار به روشهای مختلف امکانپذیر است که منجر به خواص کلاسیک میشود. با این حال، ما در این مطلب روی عملگرهای ریمان لیوویل یا R-L تمرکز میکنیم، زیرا آنها به سادگی با «عملگرهای کپوتو» (Caputo Operators) ارتباط نزدیکی دارند و پرکاربردترین اپراتورها هستند.
یکی دیگر از ویژگیهای جالب عملگر RL «غیرمحلی بودن» (Nonlocality) است. وقتی مقدار یک مشتق مرتبه صحیح را در یک نقطه محاسبه میکنیم، مقدار حاصل فقط به آن نقطه بستگی دارد. این خاصیت به ظاهر بدیهی «محلی بودن» (Locality) نامیده میشود. اما در مورد مشتقات مرتبه کسری قضیه متفاوت است. مشتق مرتبه کسری از انتگرالگیری روی طیف وسیعی از مقادیر به دست میآید و وابستگی شدید به کران پایینی انتگرالگیری دارد، به طوری که باید مشتق مرتبه کسری را به درستی نوشته باشیم:
$$ \large D _ { a } ^ { \alpha } f ( t ) = \frac { 1 }{ \Gamma ( \lceil \alpha \rceil - \alpha ) } \frac { d ^ { \lceil \alpha \rceil } }{ d t ^ { \lceil \alpha \rceil } } \int _ { a } ^ { t } ( t -\tau ) ^ { \lceil \alpha \rceil - \alpha - 1 } f ( \tau ) d \tau $$
حالت $$a = 0 $$ در هنگام تجزیه و تحلیل سیستمهای فیزیکی معمول است، زیرا اغلب متغیر وابسته زمان است و مشتق کسری در هر لحظه معین به حالت سیستم در گذشته بستگی دارد، یعنی کل زمان از شروع آزمایش در $$ t=0$$.
این غیرمحلی بودن یکی از محرکهای اصلی گرایش به حسابان کسری در کاربردهای مختلف است. بسیاری از پدیدههای فیزیکی جالب یک ویژگی دارند که به اثرات حافظه معروف است، به این معنی که وضعیت آنها تنها به زمان و موقعیت فعلی بستگی ندارد، بلکه به حالات قبلی نیز وابسته است. به عنوان مثال، میتوان یک قطعه مدار الکتریکی را تصور کرد که مقاومت آن به تمام باری (Charge) بستگی دارد که در طول زمان مشخص از آن عبور کرده است. مدلسازی و تجزیه و تحلیل سیستمهایی با اثرات حافظه با معادلات دیفرانسیل کلاسیک میتواند بسیار دشوار باشد، اما غیرمحلی بودن به مشتقات کسری این قابلیت را میدهد تا اثرات حافظه را پوشش دهد. بنابراین، حسابان کسری ابزاری بسیار مفید برای تجزیه و تحلیل این دسته از سیستمها است.
غیرمحلی بودن دلیلی نیز هست که باید در مشخص کردن بحث درباره مشتق RL چپ دقت کنیم. همچنین میتوان مرتبه انتگرالگیری را برای تعریف مشتق کسری سمت راست تغییر داد:
$$ \large _ { R } D _ { a } ^ { \alpha } f ( t ) = \frac { 1 } { \Gamma ( \lceil \alpha \rceil - \alpha ) } \frac { d ^ { \lceil \alpha \rceil } } { d t ^ { \lceil \alpha \rceil } } \int _ { t } ^ { a } ( t - \tau ) ^ { \lceil \alpha \rceil - \alpha - 1 } f ( \tau ) d \tau $$
مشتق کسری RL سمت راست با وجود ظاهر مشابه، اساساً با مشتق کسری RL سمت چپ تفاوت دارد. مشتقات کسری سمت راست به اندازه مشتقات کسری سمت چپ مطالعه نشدهاند و در موارد کاربردی چندان مفید نیستند. برای درک دلیل این موضوع، توجه کنید که ویژگی غیرمحلی بودن در مورد RLFD چپ چیست: این ویژگی بدین معناست که وضعیت یک سیستم فیزیکی به حالت آن در زمانهای گذشته بستگی دارد. اگر یک RLFD راست یک سیستم فیزیکی را توصیف کند، آنگاه حالت آن سیستم در یک زمان معین به حالت آینده آن بستگی دارد که از نظر فیزیکی معقول نیست. از آنجا که بیشتر تحقیقات مربوط به حسابان مرتبه کسری بر کاربردها متمرکز است، مشتقات کسری سمت راست فعلاً فقط برای نظریهپردازان جذاب است.
مشتقات مرتبه کسری برخی توابع پایه
مشتق مرتبه کسری توابع توانی با $$ n \ge 0 $$ به صورت زیر است:
$$ \large D ^ { \alpha } \left ( t ^ { n } \right ) = \frac { \Gamma ( n + 1 ) } { \Gamma ( n + 1 - \alpha ) } t ^ { n -\alpha } $$
برای $$ n = 0 $$، میبینیم که مشتق کسری یک عدد ثابت غیرصفر خواهد بود. شبهمشتق $$ f ( t) =1$$ نیز به صورت زیر است:
$$ \large D ^ { \frac { 1 } { 2 } } ( 1 ) = \frac { 1 } { \sqrt { \pi t } } $$
برای تابع سینوس نیز داریم:
$$ \large D ^ { \alpha } ( \sin ( t ) ) = \sin \left ( t + \frac { \alpha \pi } { 2 } \right ) $$
عبارت بالا این گفته را تأیید میکند که مشتق کسری را میتوان به عنوان یک تبدیل بین توابع و مشتقات آنها در نظر گرفت. تغییر $$\alpha$$ به سادگی سبب پیشرفت فاز میشود، تا جایی که در $$ \alpha = 1 $$ تابع کسینوس را خواهیم داشت.
مشتق مرتبه کسری تابع نمایی نیز به صورت زیر است:
$$ \large D ^ \alpha ( e ^ { k t } ) = k ^ \alpha e ^ { k t } $$
تفسیر حسابان کسری
هنوز مشخص نیست که چگونه باید عملگرهای کسری را از نظر هندسی و فیزیکی به همان روشی که برای عملگرها در حسابان کلاسیک انجام میدهیم تفسیر کنیم. این موضوع یک زمینه پژوهشی فعال است و وقتی این مسئله حل شود، احتمالاً نتایج بسیار خوبی در فیزیک و مهندسی خواهد داشت.
در این میان، سادهترین کار این است که رویکردی را دنبال کنیم که «الیور هویساید» (Oliver Heaviside) در هنگام مواجهه با عملگرهای مرتبه کسری در طول توسعه حسابان عملیاتی خود داشت. او بیان کرد که باید پذیرفت این عملگرها به عنوان دستهای از اشیاء به خودی خود وجود دارند و مجموعه خاصی از قوانین را دنبال میکنند. اگر قوانین را بدانید، خواهید فهمید که به دنبال چه هستید.
مسئله خم همزمانی
«نیلز آبل» (Neils Abel) عنوان اولین ریاضیدانی بود که ایدههای اصلی حسابان کسری را در هنگام تجزیه و تحلیل مسئله خم همزمانی (Tautochrone) توسعه داد. مسئله خم همزمانی، در واقع مسئله یافتن یک منحنی است که وقتی یک توپ را روی آن رها میکنیم که به پایین منحنی میلغزد، زمان لازم برای رسیدن به پایین منحنی مستقل از ارتفاع اولیه باشد.
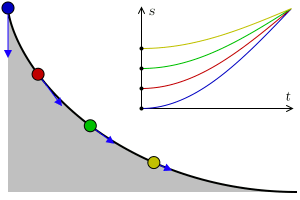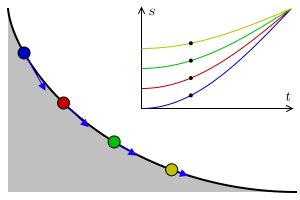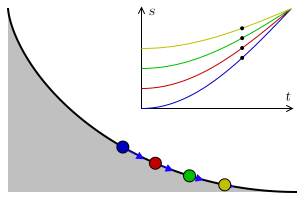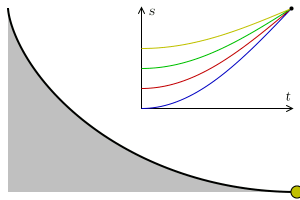
آبل برای دستیابی به معادله انتگرال زیر از استدلال فیزیک پایه استفاده کرد که زمان رسیدن به انتهای منحنی را به ارتفاع اولیه مربوط میکند:
$$ \large T \left ( y _ { 0 } \right ) = \frac { 1 } { \sqrt { 2 g } } \int _ { 0 } ^ { y _ { 0 } } \frac { 1 } { \sqrt { y _ { 0 } - y } } \frac { d s } { d y } d y $$
در رابطه بالا، $$ s $$ پارامتر طول قوس است که مسئله را حل میکند. باید این معادله را برای $$ds/dy$$ حل کنیم. میتوانستیم این مسئله را با استفاده از کانوولوشن و تبدیل لاپلاس حل کنیم، همانطور که آبل نیز این کار را انجام داد. از طرف دیگر، میتوانیم همه این موارد را کوتاهتر کنیم و از این نکته استفاده کنیم که این عبارت را در سمت راست میتوان بر $$\Gamma (1/2) = \sqrt \pi $$ تقسیم کرد تا به یک شبهانتگرال تبدیل شود. با تقسیم هر طرف این معادله بر $$\sqrt \pi$$ و بردن $$\sqrt{2g}$$ به سمت چپ و قرار دادن $$ T ( y_ 0 ) = T_ 0$$ (زیرا زمان سقوط نسبت به ارتفاع اولیه ثابت است)، داریم:
$$ \large \sqrt { \frac { 2 g } { \pi } } T _ { 0 } = I ^ { \frac { 1 } { 2 } } \left ( \frac { d s } { d y } \right ) $$
میدانیم که چگونه اپراتور شبهانتگرال را حذف کنیم. کافی است از دو طرف معادله شبهمشتق بگیریم. در نتیجه، مسئله فوراً حل میشود:
$$ \large \begin {align*}
\frac { d s } { d y } & = D ^ { \frac { 1 } { 2 } } \left ( \sqrt { \frac { 2 g } { \pi } } T _ { 0 } \right ) \\ & =
\sqrt { \frac { 2 g } { \pi } } \frac { T _ 0 } { \sqrt { y } }
\end {align*} $$
منحنی توصیف شده توسط این معادله (یک چرخزاد) خم همزمانی نامیده می شود.
این مسئله مصداق اصلی استفاده از حسابان کسری برای مسائل موجود است. به طور معمول، آنچه رخ میدهد این است که هنگام تجزیه و تحلیل یک سیستم، به طور تصادفی با یک عبارت ریاضی روبرو می شویم که یک عملگر کسری است و بنابراین میدانیم که میتوانیم قوانین عملگرهای کسری را در آن سیستم اعمال کنیم.
اگر مطلب بالای برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش مبانی آنالیز حقیقی
- مجموعه آموزشهای مهندسی کنترل
- آموزش ریاضی مهندسی (مرور و حل مساله)
- نظریه آشوب — از صفر تا صد
- فراکتال چیست؟ — به زبان ساده
- سیستم پسیو در مهندسی کنترل — به زبان ساده
^^











چرا در این نوشته و سایر نوشتههای مشابه در فرادرس اثری از منبع و مرجع نیست؟!
با سلام؛
منبع تمامی مطالب مجله فرادرس اگر ترجمه باشند در انتهای مطلب و پیش از نام نویسنده آورده شدهاند.
با تشکر از همراهی شما با مجله فرادرس
با سلام..با تشکر از درس نامه مه اراده دادید … اگر مقدور باشه از مشتقات مرتبه کسری توزیع شده در حوزه زمان با استفاده از تقریب موجک ها هم همانند این درسنام هتفسیر شود ممنون میشویم.باتشکر.