تابع هموگرافیک – از صفر تا صد

در آموزش‌های قبلی مجله فرادرس با توابع گویا آشنا شدیم. دیدیم که این توابع به فرم حاصل تقسیم دو چندجمله‌ای هستند. در این آموزش با نوع خاصی از این توابع آشنا می‌شویم که درجه چندجمله‌ای‌های صورت و مخرج آن‌ها برابر با یک است. به این نوع توابع خاص، تابع هموگرافیک می‌گوییم.

تابع گویا چیست؟

«تابع گویا» (Rational Function) تابعی است که می‌توان آن را به صورت تقسیم دو تابع چندجمله‌ای $$P ( x )$$ و $$Q(x) \neq 0$$ نوشت:

$$\large f ( x ) = \dfrac { P ( x ) }{ Q ( x ) } = \dfrac { a _ p x ^ p + a _ { p − 1 } x ^{ p − 1 } + \cdots + a _ 1 x + a _ 0 }{ b _ q x ^ q + b _ { q − 1 } x ^ { q − 1 } + \cdots + b_ 1 x + b _ 0 }$$

تابع هموگرافیک چیست؟

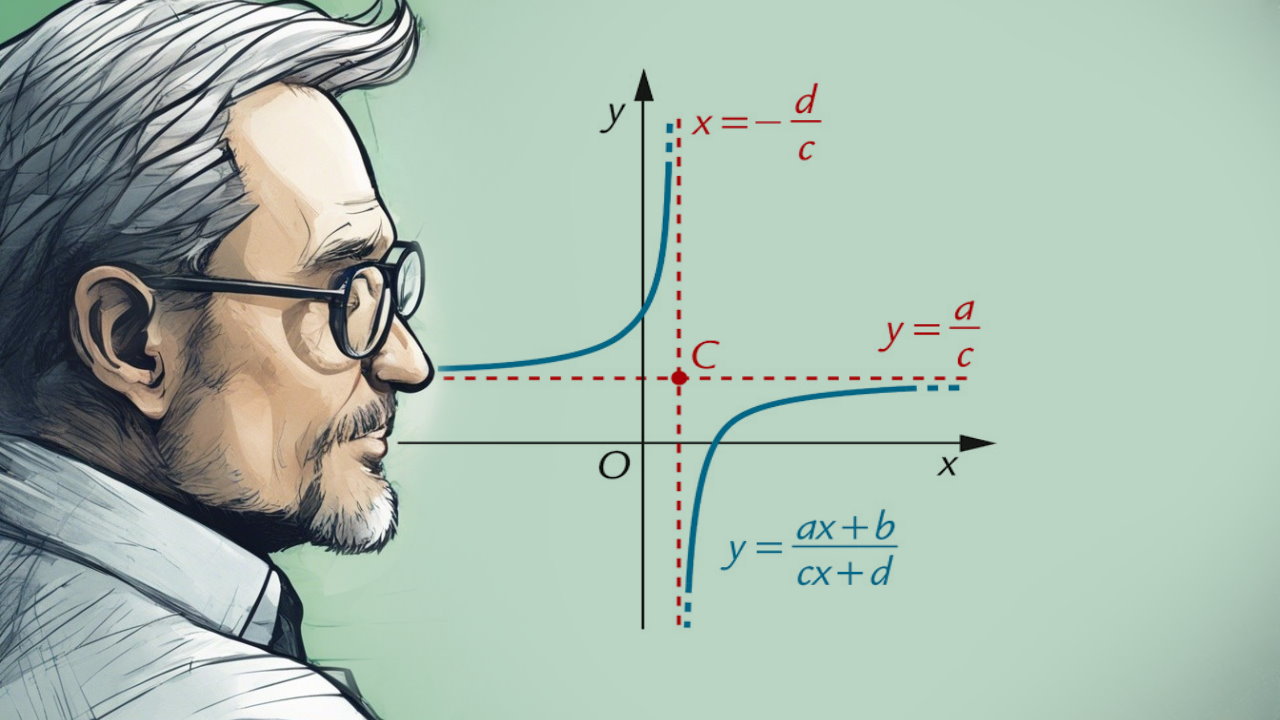
«تابع هموگرافیک» (Homographic Function) تابع گویایی است که چندجمله‌ای صورت و مخرج آن درجه اول هستند:

$$\large f \left( x \right)=\dfrac {ax+b} {cx+d}$$

که در آن، $$c \neq 0$$.

اگر $$c$$ برابر با صفر باشد، تابع $$f$$ یک تابع چندجمله‌ای درجه اول یا همان تابع خطی خواهد بود. همچنین، اگر $$\frac ac = \frac bd$$ یا $$ad-bc = 0$$، تابع ثابت و موازی محور $$x$$ خواهد بود. شکل تابع هموگرافی یک هذلولی متساوی‌الساقین (متساوی‌القطرین) است.

رسم تابع هموگرافیک

برای رسم تابع هموگرافیک، ابتدا مجانب‌های قائم و افقی را به دست می‌آوریم، سپس محل برخورد تابع با محورهای $$x$$ و $$y$$ را مشخص می‌کنیم. نمودار تابع هموگرافیک دو شاخه دارد که هر دو در بازه تعریفشان یا اکیداً صعودی یا اکیداً نزولی هستند. این موضوع را می‌توان با محاسبه مشتق تابع تعیین کرد. دقت کنید که در بازه کل اعداد حقیقی توابع هموگرافیک یکنوا نیستند.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

تعیین مجانب قائم تابع هموگرافیک

مجانب قائم تابع $$y = f ( x )$$ مقادیری از $$x$$ است که به ازای آن مخرج تابع برابر با صفر می‌شود. بنابراین، می‌توان گفت مجانب قائم تابع هموگرافیک $$f \left( x \right)=\dfrac {ax+b} {cx+d}$$ به صورت زیر به دست می‌آید:‌

$$\large c x + d =0 \Rightarrow x = - \frac d c$$

بنابراین، خط $$x = - \frac d c$$ مجانب قائم تابع هموگرافیک است. به عبارتی، داریم:

$$\large \lim _{x \to -\frac d c ^+} \frac {a x + b }{c x + d} = - \infty (\text{or} +\infty) ,\;\;\; \lim _{x \to -\frac d c ^-} \frac {a x + b }{c x + d} = + \infty (\text{or} -\infty)$$

تعیین مجانب افقی تابع هموگرافیک

مجانب افقی تابع $$y = f ( x )$$ خطی است که با میل $$x$$ به بینهایت منحنی تابع به آن خط میل می‌کند.

با توجه به تعریف بالا، مجانب افقی تابع $$f \left( x \right)=\dfrac {ax+b} {cx+d}$$ به صورت زیر محاسبه می‌شود:

$$\large \lim _{x \to \pm \infty } \frac {a x + b }{c x + d} =0^\pm \Rightarrow y = \frac a c , \;\;\; \lim _{x \to \pm \infty } \frac {a x + b }{c x + d} =0^ \mp \Rightarrow y = \frac a c$$

تعیین برخورد منحنی با محورهای مختصات

برای تعیین محل برخورد نمودار با محور $$x$$، باید مقدار $$y$$ را برابر با صفر قرار دهیم:

$$\large y = 0 \Rightarrow 0=\frac {ax + b }{c x + d } \Rightarrow ax + b = 0 \Rightarrow x = \frac {-b }{a}$$

محل برخورد نمودار با محور $$y$$ نیز با صفر قرار دادن $$x$$ محاسبه می‌شود:

$$\large x = 0 \Rightarrow y=\frac {0 + b }{0 + d }= \frac {b }{d}$$

البته تابع هموگرافیک $$f ( x ) = \frac {b}{cx}$$ با محور مختصات برخوردی ندارد.

تعیین شیب شاخه‌های تابع

تعیین جهت شیب شاخه‌های تابع با مشتق گرفتن از آن قابل انجام است:

$$\large f' (x ) = \frac {a (cx+d)-c (ax+b)}{ ( c x + d ) ^ 2}= \frac {ad-bc}{ ( c x + d ) ^ 2}$$

همان‌طور که می‌بینیم، اگر $$ad-bc>0$$ باشد، شیب مثبت و اگر $$ad-bc<0$$ باشد، شیب منفی خواهد بود.

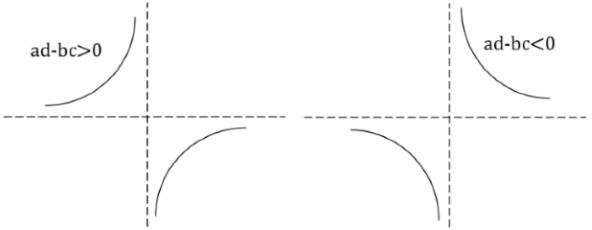
همان‌‌گونه که در منحنی‌ها و مقدار مشتق می‌بینیم، تابع هموگرافیک همواره یک به یک است و نقطه عطف و اکسترمم نیز ندارد.

دامنه و برد تابع هموگرافیک

دامنه تابع هموگرافیک همه اعداد حقیقی به جز آن‌هایی است که مخرج را صفر می‌کنند، زیرا مخرج صفر تعریف نشده است. با توجه به مجانب قائم تابع هموگرافیک، می‌توان گفت دامنه آن به صورت زیر است:

$$\large \mathbb R - \{ \frac {-d}{c} \}$$

برد تابع هموگرافیک نیز، همه اعداد حقیقی است به جز نقاطی که در آن‌ها $$x$$ تعریف نشده است. یعنی، مجموعه زیر:

$$\large \mathbb R - \{ \frac {a}{c} \}$$

تقارن تابع هموگرافیک

محل برخورد مجانب‌های تابع هموگرافیک، یعنی $$( \frac {-d}{c} , \frac a c )$$ مرکز تقارن آن است. تقارن بین ربع اول و سوم و همچنین دوم و چهارم برقرار است. محورهای تقارن تابع هموگرافیک نیز دو خط عمود بر هم با شیب‌های $$+1$$ و $$-1$$ هستند که از مرکز تقارن می‌گذرند. معادله این دو خط تقارن تابع هموگرافیک به صورت زیر است:

$$\large y - \frac a c = \pm \left ( x + \frac d c \right )$$

مثال‌های تابع هموگرافیک

در این بخش، چند مثال را درباره تابع هموگرافیک حل می‌کنیم.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

مثال اول تابع هموگرافیک

نمودار تابع هموگرافیک $$f ( x ) = \frac 1 x$$ را رسم کنید.

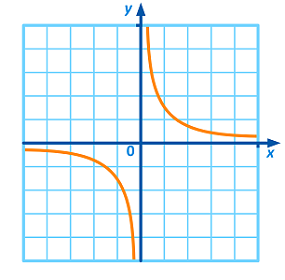
حل: ابتدا مجانب‌ها را به دست می‌آوریم که $$x = 0$$ و $$y = 0$$ هستند. تابع با محورهای مختصات برخورد ندارد. با توجه به مشتق $$f' (x ) = -\frac { 1 } { x ^ 2 }$$، شاخه‌های تابع نزولی هستند.

نمودار این تابع به صورت زیر است.

مثال دوم تابع هموگرافیک

تابع هموگرافیک زیر را در نظر بگیرید:

$$\large f ( x ) = a x + \frac { { { x } ^ { 2 } }} { x - 1 }$$

نمودار این تابع از کدام ربع دستگاه مختصات عبور می‌کند؟

حل: ابتدا تابع را به صورت زیر می‌نویسیم:

$$\large f ( x ) = a x + \frac { { { x } ^ { 2 } } } { x - 1 } = \frac { a { { x } ^ { 2 } } - a x + { { x } ^ { 2 } } } { x - 1 } = \frac { ( a + 1 ) { { x } ^ { 2 } } - a x } { x - 1 }$$

اکنون مقدار $$a$$ را به گونه‌ای تعیین می‌کنیم که تابع هموگرافیک باشد. بدین منظور، ضریب $$x ^ 2$$ باید صفر شود:

$$\large a + 1 = 0 \Rightarrow a = - 1$$

بنابراین، تابع هموگرافیک به صورت زیر است:

$$\large f ( x ) = \frac { x } { x - 1 }$$

برای رسم نمودار تابع، مجانب‌های قائم و افقی آن را به دست می‌آوریم. مجانب قائم برابر است با:

$$\large x = - \frac {-1}{1} = 1$$

مجانب افقی نیز به صورت زیر به دست می‌آید:

$$\large y = \frac 1 1 = 1$$

اکنون که مجانب‌ها را داریم، برای رسم نمودار تابع، مشتق آن را محاسبه می‌کنیم:

$$\large { f }' ( x ) = \frac { - 1 } { { { ( x - 1 ) } ^ { 2 } } } \lt 0$$

می‌بینیم که شیب نمودار همواره منفی است. بنابراین، نمودار تابع هموگرافیک به شکل زیر خواهد بود.

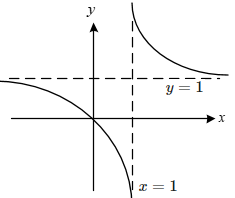
همان‌طور که می‌بینیم، نمودار تابع از ربع اول، دوم و چهارم عبور می‌کند.

مثال سوم تابع هموگرافیک

دامنه تابع $$f(x) = \dfrac{x+2}{x}$$ را محاسبه کنید.

حل: برای آنکه تابع $$f$$ تعریف شده باشد، مخرج $$x$$ باید مخالف صفر باشد. بنابراین، دامنه تابع $$f$$ به صورت زیر خواهد بود:

$$\large (-\infty , 0) \cup (0,+\infty)$$

مثال چهارم تابع هموگرافیک

دامنه تابع $$g(x) = \dfrac{x-1}{x-2}$$ چیست؟

حل: برای آنکه $$g$$ تعریف شده باشد، مخرج $$x - 2$$ باید مخالف صفر باشد. ابتدا مقدار $$x$$ را که مخرج به ازای آن برابر با صفر می‌شود به دست می‌آوریم:

$$\large x - 2 = 0 \Rightarrow x = 2$$

بنابراین، دامنه تابع $$g$$ همه اعداد حقیقی به جز $$x = 2$$ است:

$$\large (-\infty , 2) \cup (2,+\infty)$$

مثال پنجم تابع هموگرافیک

انتگرال تابع هموگرافیک $$\int { { \frac { { x + 2 } } { { x – 1 } } } d x }$$ را محاسبه کنید.

حل: انتگرالده را به صورت مجموع یک عدد و یک کسر سره می‌نویسیم:

$$\large \frac { { x + 2 } } { { x – 1 } } = 1 + \frac { 3 } { { x – 1 } } .$$

اکنون می‌توانیم به سادگی انتگرال را محاسبه کنیم:

$$\large \begin {align*} \int { \frac { { x + 2 } } { { x – 1 } } d x } & = { \int { \left ( { 1 + \frac { 3 } { { x – 1 } } } \right ) d x } } \\ & = { \int { d x } + 3 \int { \frac { { d x } } { { x – 1 } } } } \\ & = { x + 3 \ln \left | { x – 1 } \right | + C . } \end {align*}$$

مثال ششم تابع هموگرافیک

اگر تابع هموگرافیک و وارون آن برابر باشند، ثابت کنید رابطه $$a + d = 0$$ برقرار است.

حل: تابع هموگرافیک $$y= \frac{ax+b}{cx+d}$$ را در نظر می‌گیریم. با عوض کردن جای $$x$$ و $$y$$ وارون تابع را می‌نویسیم:

$$\large x= \frac { a y + b } { c y + d } \Rightarrow c y x + d x = a y + b \Rightarrow c y x - a y = - d x + b \\ \large \Rightarrow y ( c x - a ) = - d x + b \Rightarrow y = \frac { - d x + b } { c x - a }$$

برای آنکه تابع هموگرافیک و وارونش برابر باشند، باید تساوی $$a=-d$$ را داشته باشیم که معادل $$a + d = 0$$ است.