تابع توانی و تابع چند جمله ای | به زبان ساده

در آموزش‌های پیشین از مجموعه مطالب ریاضی مجله فرادرس، با مفاهیم تابع و موضوعاتی مانند ماکزیمم و مینیمم تابع، دامنه و برد تابع، مجانب تابع، معکوس تابع و تابع یک به یک و پوشا آشنا شدیم. در این آموزش، با تابع توانی و تابع چند جمله ای آشنا می‌شویم.

تابع توانی چیست؟

فرض کنید گونه خاصی از پرندگان در یک جزیره کوچک زندگی می‌کنند. جمعیت این پرندگان در چند سال گذشته در جدول نشان داده شده است.

جمعیت پرندگان را می‌توان با تابع $$P(t)=−0.3t^3+97t+800$$ تخمین زد، که در آن، $$P ( t )$$ جمعیت پرندگان جزیره را در $$t$$ سال پس از سال ۲۰۰۹ نشان می‌دهد. می‌توانیم از این مدل برای تخمین حداکثر جمعیت پرندگان و زمان آن استفاده کنیم. همچنین می‌توانیم با این مدل پیش‌بینی کنیم که چه زمانی پرندگان جزیره منقرض می‌شوند. در ادامه، چنین توابعی را معرفی خواهیم کرد که تابع توانی و تابع چندجمله‌ای نام دارند و با استفاده از آن‌ها می‌توان چنین تغییراتی را پیش‌بینی کرد.

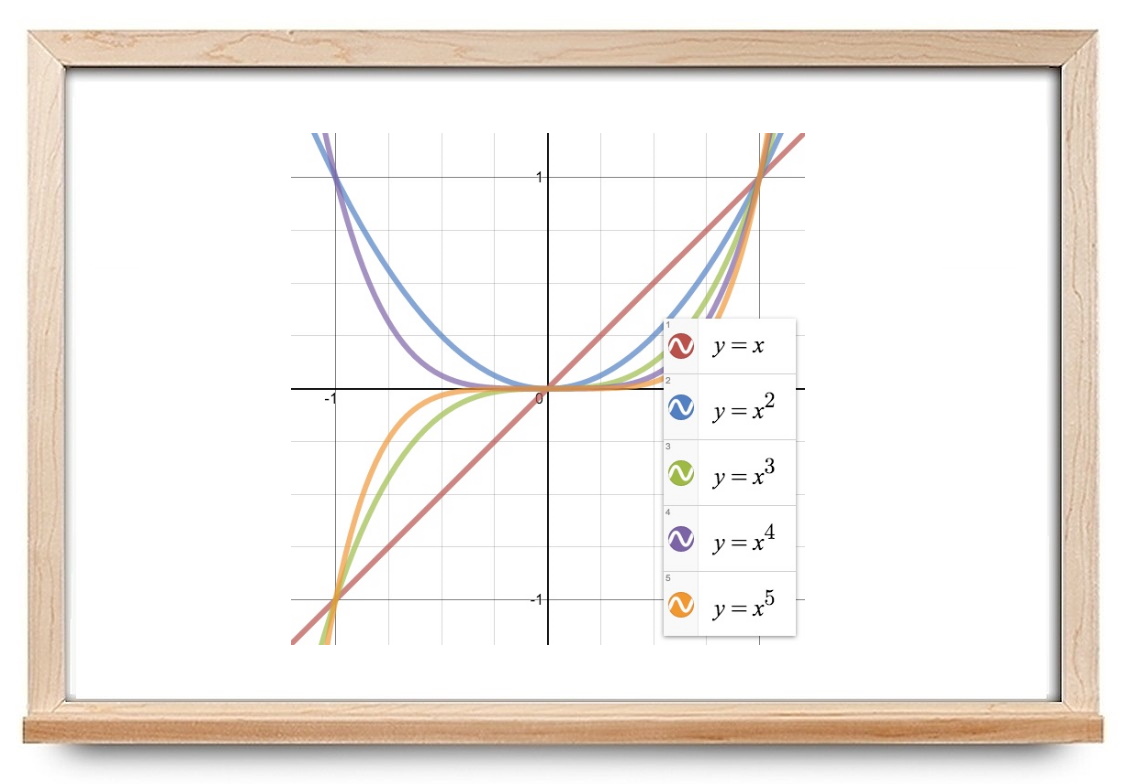
برای درک بهتر مثال پرنده‌ها، باید با نوع خاصی از توابع آشنا شویم. تابع توانی تابعی با یک جمله واحد است که حاصل‌ضرب یک عدد حقیقی و یک متغیر است که به یک توان یک عدد حقیقی ثابت رسیده است (عددی که در متغیر ضرب می‌شود، به عنوان ضریب شناخته می‌شود). به عنوان یک مثال، تابع مساحت یا حجم را در نظر بگیرید. تابع مساحت یک دایره با شعاع $$r$$ برابر است با:

$$\large A(r)={\pi}r^2$$

و تابع حجم یک کره با شعاع $$r$$ نیز به شکل زیر است:

$$\large V(r)=\dfrac{4}{3}{\pi}r^3$$

هریک از این مثال‌ها یک تابع توانی است، زیرا از یک ضریب $$\pi$$ یا $$\dfrac{4}{3}{\pi}$$ ضرب در متغیر $$r$$ به توان یک عدد حقیقی تشکیل شده است.

تعریف تابع توانی

یک «تابع توانی» (Power Function) تابعی است که می‌توان آن را به فرم زیر نمایش داد:

$$ \large f(x)=kx^p \label{power} $$

که در آن، $$k$$ و $$p$$ اعدادی حقیقی هستند و $$k$$ به عنوان ضریب شناخته می‌شود.

اما آیا $$f(x)=2^x$$ یک تابع توانی است؟ خیر. طبق تعریفی که بیان کردیم، تابع توانی از یک پایه متغیر به توان یک عدد ثابت تشکیل می‌شود. تابع این پرسش «تابع نمایی» (Exponential Function) نامیده می‌شود.

مثال ۱: کدام‌یک از توابع زیر تابع توانی هستند؟

• تابع ثابت $$f ( x ) = 1$$
• تابع همانی $$f ( x ) = x$$
• تابع درجه دو $$f ( x ) = x ^ 2$$
• تابع درجه سه $$f ( x ) = x ^ 3$$
• تابع وارون $$f ( x ) = \frac { 1} { x }$$
• تابع وارون مربع $$f ( x ) = \frac { 1 } { x ^ 2 }$$
• تابع ریشه دوم $$f ( x ) = \sqrt { x }$$
• تابع ریشه سوم $$f ( x ) = \sqrt [3] { x }$$

پاسخ: همه این توابع تابع توانی هستند. توابع ثابت و همانی توابع توانی هستند، زیرا می‌توان آن‌ها را به ترتیب، به صورت $$f ( x ) = x ^ 0$$ و $$f ( x ) = x ^ 1$$ نوشت. توابع درجه دوم و درجه سوم تابع توانی هستند، زیرا می‌توان آن‌ها را به ترتیب، به صورت $$f ( x) = x ^ 2$$ و $$f ( x ) = x ^ 3$$ نوشت. توابع وارون و وارون مجذور توابع توانی با توان‌های منفی هستند، زیرا می‌توان آن‌ها را به صورت $$f(x)=x^{1/2}$$ یا $$f(x)=x^{1/3}$$ نوشت.

رفتار حدی تابع توانی

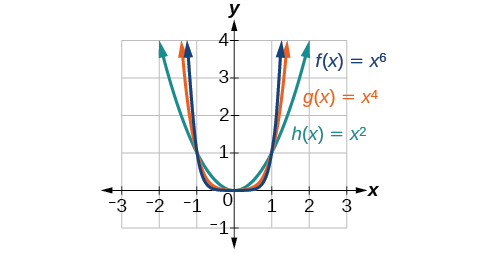
شکل ۲ نمودارهای $$f(x)=x^2$$، $$g(x)=x^4$$ و $$h(x)=x^6$$ را نشان می‌دهد که همه توابعی توانی با توان‌های زوج هستند.

توجه کنید که این نمودارها شکل‌های مشابهی دارند و شبیه تابع درجه دوم هستند. البته، وقتی توان زیاد می‌شود، نمودارها در نزدیکی مبدأ تخت‌تر شده و با زاویه تندتری از آن دور می‌شوند.

برای توصیف رفتار این توابع، وقتی عدد توان بزرگ و بزرگ‌تر می‌شود، از ایده بینهایت استفاده می‌کنیم. از نماد $$\infty$$ برای مثبت بینهایت و $$- \infty$$ برای منفی بینهایت استفاده می‌کنیم. وقتی می‌گوییم «$$x$$ به بینهایت میل می‌کند»، که آن را به شکل نمادی $$x{\rightarrow}\infty$$ نشان می‌دهیم، در حال توصیف یک رفتار هستیم و در واقع، می‌گوییم $$x$$ بدون کران در حال افزایش است. وقتی توان توابع زوج باشد، با کاهش یا افزایش بدون کران $$x$$، مقادیر خروجی اعداد مثبت بسیار بزرگی خواهند شد. در واقع، می‌توان به فرم نمادین نوشت:

$$\large \text {as } x { \rightarrow } { \pm }{ \infty } , f ( x ) { \rightarrow }  { \infty }$$

شکل ۳ نمودارهای $$f ( x ) = x ^ 3$$، $$g ( x ) = x ^ 5$$ و $$h ( x ) = x ^ 7$$ را نشان می‌دهد که همه توابع توانی با توان فرد هستند. توجه کنید که این نمودارها نیز مشابه نمودار تابع درجه دوم هستند. مجدداً، وقتی توان افزایش پیدا کند، نمودارها حول مبدأ صاف‌تر شده و با شیب تندتری از مبدأ دور می‌شوند.

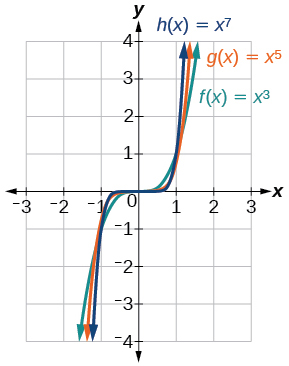
این مثال‌ها نشان می‌دهند که $$f(x)=x^n$$ نشان دهنده تقارن یک دسته از توابع است. ابتدا، در شکل ۲ می‌بینیم که توابع زوج به فرم $$f ( x ) = x ^ n$$ که در آن، $$n$$ زوج است، حول نسبت به محور $$y$$ متقارن هستند. در شکل ۳ می‌بینیم که توابع فرد به فرم $$f ( x ) = x ^ n$$ با $$n$$ فرد، نسبت به مبدأ متقارن هستند.

وقتی $$x$$ به منفی بینهایت میل کند، این توابع توانی فرد $$f ( x )$$ بدون کران کاهش پیدا می‌کنند. وقتی $$x$$ به مثبت بینهایت میل کند، $$f ( x )$$ بدون محدودیت افزایش پیدا می‌کند. به فرم نمادین، می‌توانیم بنویسیم:

$$\large \begin {align} \text {as } x { \rightarrow } - { \infty } , \; f ( x ) { \rightarrow }  - { \infty } \\ \text {as } x { \rightarrow } { \infty } , \; f ( x ) { \rightarrow } { \infty } \end {align}$$

رفتار نمودار یک تابع، وقتی مقادیر ورودی بسیار کوچک شوند ($$x { \rightarrow } − { \rightarrow } − { \infty }$$) و و وقتی بسیار بزرگ ($$x{\rightarrow}{\rightarrow}{\infty}$$) شوند، رفتار حدی نهایی تابع گفته می‌شود. می‌توانیم از واژه‌ها یا نمادها برای توصیف رفتار حدی استفاده کنیم.

شکل ۴ رفتار حدی توابع توانی به فرم $$f ( x ) = k x ^ n$$ را نشان می‌دهد که در آن، $$n$$ بسته به توان و ضریب، یک عدد صحیح نامنفی است.

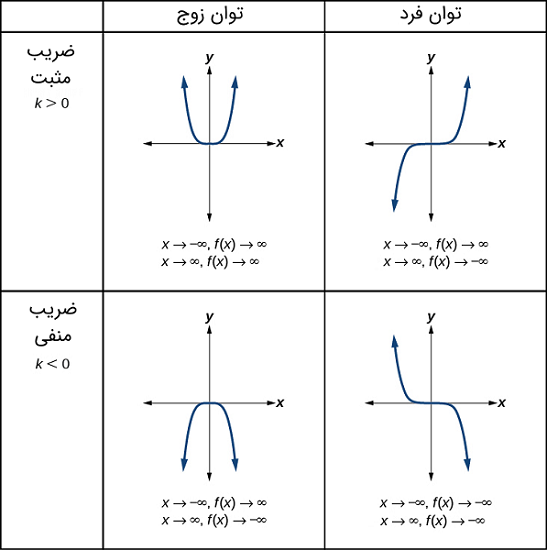
برای تابع توانی $$f(x)=kx^n$$ که در آن، $$n$$ یک عدد صحیح نامنفی است، رفتار حدی را طی مراحل زیر تعیین می‌کنیم:

• (۱) زوج یا فرد بودن توان را مشخص کنید.
• (۲) مثبت یا منفی بودن ثابت را تعیین کنید.
• (۳) برای مشخص کردن رفتار حدی از شکل ۴ استفاده کنید.

مثال ۲: رفتار حدی تابع $$f ( x ) = x ^ 8$$ را توصیف کنید.

پاسخ: ضریب $$1$$ (مثبت) و نمای تابع توانی $$8$$ (یک عدد زوج) است. وقتی $$x$$ به بینهایت میل می‌کند، خروجی (مقدار $$f ( x )$$) بدون کران افزایش پیدا می‌کند. بنابراین، می‌توان نوشت: وقتی $$x \to  \infty$$، آنگاه $$f ( x ) \to \infty$$. وقتی $$x$$ به منفی بینهایت میل کند، خروجی بدون کران افزایش پیدا می‌کند. به فرم نمادین، وقتی $$x \to \infty$$، آنگاه $$f ( x ) \to \infty$$. این تابع به صورت گرافیکی در شکل ۵ نشان داده شده است.

$$f ( x ) = x ^ 8$$" width="487" height="330">

مثال ۳: رفتار حدی نمودار تابع $$f(x)=−x^9$$ را مشخص کنید.

پاسخ: نمای تابع توانی $$9$$ (یک عدد فرد) است. از آنجا که ضریب $$- 1$$ (منفی) است، نمودار بازتاب نمودار $$f ( x ) = x ^ 9$$ نسبت محور $$x$$ است. شکل ۶ نشان می‌دهد که وقتی $$x$$ به بینهایت میل می‌کند، خروجی بدون کران کاهش پیدا می‌کند. وقتی $$x$$ به منفی بینهایت میل کند، خروجی بدون محدودیت افزایش پیدا می‌کند. به فرم نمادین، می‌نویسیم:

$$\large \begin {align*} \text {as } x { \rightarrow } - { \infty } , \; f ( x ) { \rightarrow }  { \infty } \\ \text {as } x { \rightarrow }{ \infty } , \; f ( x ) { \rightarrow } - { \infty } \end {align*}$$

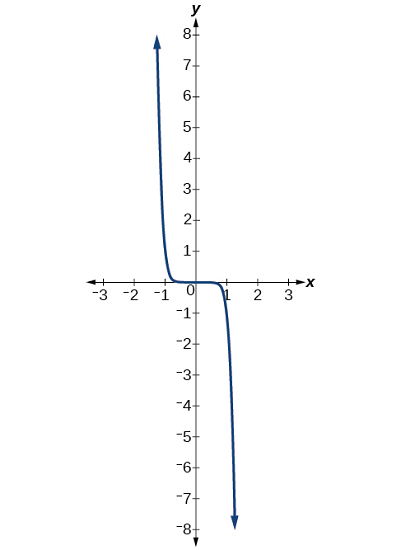$$f ( x ) = - x^ 9$$" width="401" height="550">

تابع چند جمله ‌ای

یک خط لوله نفتی را در نظر بگیرید که از خلیجی عبور کرده و مسیر آن به شکل تقریباً دایره‌ای است.

شعاع آن ۲۴ مایل است، اما این شعاع در هر هفته ۸ مایل افزایش می‌یابد. می‌خواهیم با ترکیب دو تابع، یک فرمول برای ناحیه تحت پوشش لکه نفتی بنویسیم. شعاع $$r$$ آلودگی به تعداد هفته‌هایی که سپری شده بستگی دارد. این رابطه خطی است و داریم:

$$\large r(w)=24+8w \nonumber$$

می‌توانیم این رابطه را با فرمول مساحت $$A$$ یک دایره تعیین کنیم:

$$\large A(r)={\pi}r^2 \nonumber$$

ترکیب این توابع فرمولی را برای مساحت نتیجه خواهد داد که برحسب هفته است:

$$\large \begin{align*} A(w)&=A(r(w)) \\ &=A(24+8w) \\ & ={\pi}(24+8w)^2 \end{align*}$$

با اعمال توان، فرمول زیر را خواهیم داشت:

$$\large A(w)=576{\pi}+384{\pi}w+64{\pi}w^2 \nonumber$$

این فرمول مثالی از یک تابع چندجمله‌ای است. تابع چندجمله‌ای از مجموع تعداد محدودی جمله غیرصفر تشکیل می‌شود که هر کدام از آن‌ها حاصل‌ضرب یک عدد (که ضریب جمله نامیده می‌شود) و یک متغیر به توان یک عدد صحیح نامنفی است.

تعریف توابع چند جمله ‌ای

فرض کنید $$n$$ یک عدد صحیح نامنفی باشد. یک «تابع چندجمله‌ای» (Polynomial Function) تابعی است که می‌توان آن را به فرم زیر نوشت:

$$\large f ( x ) = a _ n x ^ n + . . . + a _ 2 x ^ 2 + a _ 1 x + a _ 0$$

که فرم عمومی تابع چندجمله‌ای نامیده می‌شود. هر $$a _ i$$ یک ضریب است و می‌تواند هر عدد حقیقی باشد. هر حاصل‌ضرب $$a_ix^i$$ یک جمله تابع چندجمله‌ای نامیده می‌شود.

مثال ۴: کدام‌یک از توابع زیر چندجمله‌ای هستند؟

• $$f(x)=2x^3⋅3x+4$$
• $$g(x)=−x(x^2−4)$$
• $$h(x)=5\sqrt{x}+2$$

پاسخ: دو تابع نخست مثال‌هایی از توابع چندجمله‌ای هستند، زیرا می‌توان آن‌ها را به فرم معادله بالا نوشت که در آن، توان‌ها اعداد صحیح نامنفی هستند و ضرایب اعدادی حقیقی‌اند.

• $$f ( x )$$ را می‌توان به صورت $$f(x)=6x^4+4$$ نوشت.
• $$g ( x )$$ به شکل $$g(x)=−x^3+4x$$ نوشته می‌شود.
• $$h ( x )$$ را نمی‌توان به فرم معادله بالا نوشت و بنابراین، یک تابع چندجمله‌ای نیست.

تعیین درجه و ضریب تابع چند جمله ای

با توجه به فرم یک چندجمله‌ای، می‌توانیم تنوع بینهایتی از جملات و توان‌های متغیرها را شاهد باشیم. اگرچه ترتیب جملات در تابع چندجمله‌ای برای انجام عملیات مهم نیست، اما معمولاً جملات را به ترتیب نزولی توان یا به فرم عمومی می‌نویسیم. درجه چندجمله‌ای بالاترین توان متغیر است که در چند‌جمله‌ای وجود دارد؛ اگر متغیر به فرم عمومی باشد، درجه همان توانِ متغیرِ اول است. جمله پیشگام عبارت است از جمله‌ای با بزرگ‌ترین توان متغیر یا جمله‌ای با بالاترین درجه. ضریب پیشگام ضریب جمله پیشگام است. اغلب، چندجمله‌ای‌ها را به گونه‌ای بازنویسی می‌کنیم که توان‌ها کاهشی باشند.

وقتی یک چندجمله‌ای بدین صورت نوشته شود، می‌گوییم به فرم عمومی نوشته شده است.

برای مشخص کردن درجه و ضریب پیشگام چندجمله‌ای به صورت زیر عمل کنید:

• (۱) توان $$x$$ را برای تعیین درجه چندجمله‌ای مشخص کنید.
• (۲) جمله شامل بزرگ‌ترین توان $$x$$ را برای یافتن جمله پیشگام مشخص کنید.
• (۳) ضریب جمله پیشگام را مشخص کنید.

مثال ۵: درجه، جمله پیشگام و ضریب پیشگام توابع چندجمله‌ای زیر را مشخص کنید.

• $$\large f(x)=3+2x^2−4x^3$$
• $$\large g(t)=5t^5−2t^3+7t$$
• $$h(p)=6p−p^3−2$$

پاسخ: در تابع $$f ( x )$$، بزرگ‌ترین توان $$x$$ برابر با ۳ است، بنابراین، درجه چندجمله‌ای ۳ است. جمله پیشگام جمله‌ای شامل این درجه است، یعنی $$−4x^3$$. ضریب پیشگام، ضریب این جمله، یعنی $$- 4$$ است. برای تابع $$g ( t )$$، بزرگ‌ترین توان $$t$$ عدد ۵ است. جمله پیشگام نیز جمله‌ای شامل این درجه است، یعنی $$5 t ^ 5$$. ضریب پیشگام ضریب این جمله، یعنی ۵ است. در تابع $$h(p)$$، بزرگ‌ترین توان $$p$$ عدد ۳ است. جمله پیشگام نیز جمله‌ای شامل این درجه است، یعنی $$−p^3$$. ضریب پیشگام ضریب این جمله، یعنی $$-1$$ است.

رفتار حدی توابع چند جمله ‌ای

دانستن درجه یک تابع چندجمله‌ای برای کمک در پیش‌بینی رفتار حدی آن مفید است. برای تعیین رفتار حدی تابع چندجمله‌ای، جمله پیشگام تابع چند‌جمله‌ای را بررسی می‌کنیم. از آنجا که توان جمله پیشگام بالاترین است، با افزایش یا کاهش مقدار $$x$$، این جمله به طور قابل توجهی سریع‌تر از سایر جملات رشد خواهد کرد. برای هر چندجمله‌ای، رفتار حدی آن با رفتار حدی جمله بالاترین درجه مطابقت دارد.

مثال ۶: رفتار حدی و یک درجه ممکن برای تابع چندجمله‌ای شکل ۸ توصیف کنید.

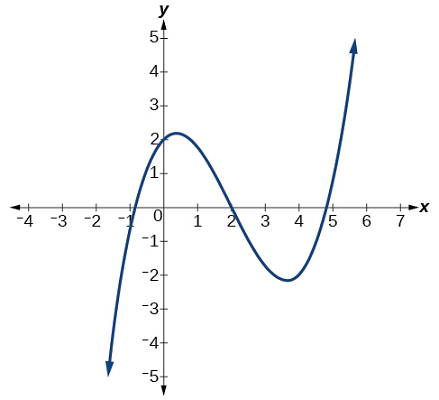
پاسخ: وقتی مقادیر ورودی $$x$$ بسیار کوچک شوند، مقادیر خروجی $$f ( x )$$ بدون کران افزایش می‌یابند. وقتی مقادیر ورودی $$x$$ بسیار کوچک شوند، مقادیر خروجی $$f ( x )$$ بدون کران کاهش می‌یابند. می‌توانیم رفتار حدی را به صورت نمادین زیر بنویسیم:

$$\large \text {as } x { \rightarrow } − { \rightarrow } − { \infty } , f ( x ) { \rightarrow } − { \rightarrow } − { \infty }$$

$$\large \text {as } x { \rightarrow } { \rightarrow } { \infty } , f ( x ) { \rightarrow } { \rightarrow } { \infty }$$

در قالب کلمات، می‌توان گفت که هرچه مقادیر $$x$$ به بینهایت نزدیک می‌شوند، مقادیر تابع به بینهایت می‌گرایند و هرچه مقادیر $$x$$ به منفی بینهایت منفی نزدیک شوند، مقادیر تابع به منفی بینهایت میل می‌کنند. می‌توانیم بگوییم این نمودار دارای یک تابع توانی درجه فرد است که بازتاب ندارد، بنابراین درجه چندجمله‌ای مروط به این نمودار باید فرد و ضریب پیشگام مثبت باشد.

مثال ۷: تابع $$f(x)=−3x^2(x−1)(x+4)$$ را در نظر بگیرید. این تابع را به فرم عمومی بنویسید و جمله پیشگام، درجه و رفتار تابع را مشخص کنید.

پاسخ: فرم عمومی را با بسط عبارت $$f ( x )$$ می‌نویسیم:

$$\large \begin {align} f ( x ) & = − 3 x ^ 2 ( x − 1 ) (x + 4 ) \\ & = − 3 x ^ 2 ( x ^ 2 + 3 x − 4 ) \\ & = − 3 x ^ 4 − 9 x ^ 3 + 1 2 x ^ 2 \end {align}$$

فرم عمومی $$f(x)=−3x^4−9x^3+12x^2$$ و جمله پیشگام $$- 3 x ^ 4$$ است. بنابراین، درجه چندجمله‌ای ۴ است. درجه زوج است و ضریب پیشگام منفی ($$-3$$) است، بنابراین، رفتار حدی به صورت زیر خواهد بود:

$$\large \text{as }x{\rightarrow}−{\infty}, f(x){\rightarrow}−{\infty}$$

$$\large \text{as } x{\rightarrow}{\infty}, f(x){\rightarrow}−{\infty}$$

رفتار محلی توابع چند جمله ‌ای

علاوه بر رفتار حدی توابع چندجمله‌ای، می‌خواهیم بدانیم که در میانه تابع چه اتفاقی می‌افتد. به طور خاص، می‌خواهیم مکان‌هایی را بیابیم که در آن‌ها رفتار نمودار تغییر می‌کند. نقطه بازگشت نقطه‌ای است که در آن، مقادیر تابع از نزولی به صعودی یا بالعکس تغییر می‌کند.

همچنین، می‌خواهیم نقاط برخورد با محورها را پیدا کنیم. مانند همه توابع، نقطه برخورد نمودار با محور $$y$$ یا همان عرض از مبداء جایی است که متغیر ورودی $$x$$ برابر با صفر است. از آنجا که چندجمله‌ای یک تابع است، تنها یک مقدار خروجی به ازای هر $$x$$ وجود دارد که مختصات نقطه به شکل $$(0,a_0)$$ خواهد بود.

برخورد با محور $$x$$ یا طول از مبداء نیز به ازای مقادیری از $$x$$ رخ می‌دهد که در آن‌ها مقدار خروجی $$y$$ برابر با صفر است. روی محور $$x$$ ممکن است چندین برخورد با نمودار وجود داشته باشد. شکل زیر را ببینید.

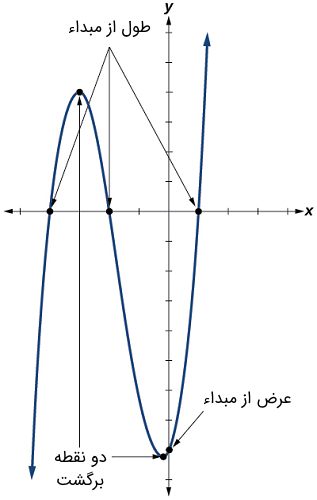
نقاط برخورد و بازگشت توابع چند جمله ‌ای

یک نقطه بازگشت، نقطه‌ای از نمودار است که در آن، جهت نمودار از صعودی به نزولی و نزولی به صعودی تغییر می‌کند. نقطه برخورد با $$y$$ نقطه‌ای است که در آن، مقدار ورودی تابع برابر با صفر است. نقطه برخورد با $$x$$ مجموعه‌ نقاطی است که در آن‌ها مقدار خروجی صفر است.

اما، چگونه نقاط برخورد یک تابع را مشخص کنیم؟ به سادگی می‌توان این کار را انجام داد:

• تقاطع با محور $$y$$ را با قرار دادن $$x =0$$ و یافتن مقدار خروجی متناظر تعیین می‌کنیم.
• تقاطع با محور $$x$$ را با حل برای آن دسته از مقادیر ورودی که خروجی را صفر می‌کنند به دست می‌آوریم.

مثال ۸: تابع چندجمله‌ای $$f(x)=(x−2)(x+1)(x−4)$$ را در نظر بگیرید که برای سادگی محاسبه محل‌های تقاطع برحسب عامل‌هایش نوشته شده است.

پاسخ: تقاطع با $$y$$ زمانی رخ می‌دهد که ورودی صفر باشد، بنابراین، $$x$$ را برابر با $$0$$ قرار می‌دهیم.

$$\large \begin{align}f(0)&=(0−2)(0+1)(0−4) \\ &=(−2)(1)(−4) \\ &=8 \end{align}$$

عرض از مبداء نقطه $$( 0  , 8 )$$ است.

تقاطع با محور $$x$$ وقتی رخ می‌دهد که خروجی صفر باشد:

$$\large \begin{align} x−2&=0 & &\text{or} & x+1&=0 & &\text{or} & x−4&=0 \\ x&=2 & &\text{or} & x&=−1 & &\text{or} & x&=4 \end{align}$$

طول از مبداء در نقاط $$( 2 , 0 )$$، $$(-1, 0 )$$، و $$( 4 , 0 )$$ رخ می‌دهد.

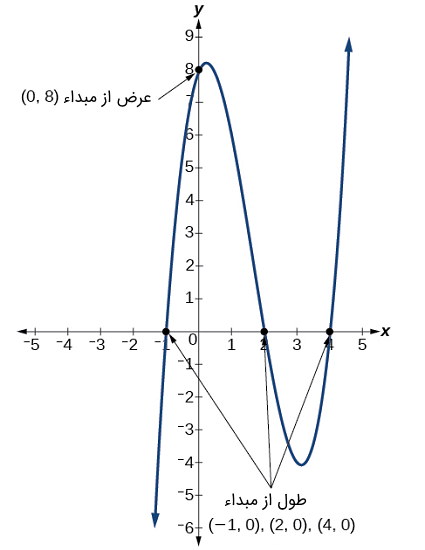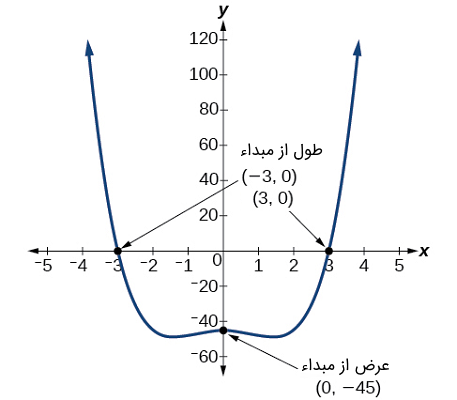
$$f(x)=(x-2)(x+1)(x-4)$$" width="425" height="550">

مثال ۹: تابع چندجمله‌ای $$f(x)=x^4−4x^2−45$$ را در نظر بگیرید. عرض از مبداء و طول از مبداء آن را بیابید.

پاسخ: تقاطع با $$y$$ وقتی رخ می‌دهد که ورودی $$x$$ صفر باشد:

$$\large \begin{align*} f(0) &=(0)^4−4(0)^2−45 \\[4pt] &=−45 \end{align*}$$

در نتیجه، عرض از مبداء نقطه $$( 0 , - 45 )$$ است.

طول از مبداء زمانی به دست می‌آید می‌دهد که خروجی برابر با صفر باشد. برای تعیین زمانی که خروجی صفر می‌شود، باید از چندجمله‌ای فاکتور بگیریم:

$$\large \begin{align*} f(x)&=x^4−4x^2−45 \\ &=(x^2−9)(x^2+5) \\ &=(x−3)(x+3)(x^2+5) \end{align*}$$

$$\large 0=(x−3)(x+3)(x^2+5)$$

$$\large \begin{align*} x−3&=0 & &\text{or} & x+3&=0 & &\text{or} & x^2+5&=0 \\ x&=3 & &\text{or} & x&=−3 & &\text{or} &\text{(no real solution)} \end{align*}$$

نقاط تقاطع با محور $$x$$، نقاط $$( 3 , 0 )$$ و $$( - 3 , 0 )$$ است. این نقاط را روی نمودار شکل ۱۱ می‌بینیم. مشاهده می‌کنیم که تابع زوج است، زیرا $$f(x)=f(−x)$$.

$$f(x)=x^4-4x^2-45$$" width="457" height="400">

مقایسه نمودارهای نرم (هموار) و پیوسته

درجه یک تابع چندجمله‌ای به ما کمک می‌کند تا تعداد تقاطع‌ها با محور $$x$$ و تعداد نقاط برگشت را تعیین کنیم. یک تابع چندجمله‌ای درجه $$n$$، حاصل‌ضرب $$n$$ عامل است، بنابراین حداکثر $$n$$ ریشه یا صفر یا طول از مبداء خواهد داشت. در واقع، طول از مبداءها همان ریشه‌های چندجمله‌ای هستند. نمودار تابع چندجمله‌ای درجه $$n$$ باید حداکثر $$n - 1$$ نقطه برگشت داشته باشد. این بدان معنی است که نمودار حداقل یک نقطه برگشت کمتر از درجه چندجمله‌ای یا کمتر از تعداد عامل‌ها دارد.

در نمودار تابع پیوسته شکستگی وجود ندارد: نمودار را می‌توان بدون برداشتن قلم از روی کاغذ رسم کرد. منحنی هموار نموداری است که هیچ شکستگی یا گوشه تیزی ندارد. نقاط برگشت یک نمودار صاف همیشه باید منحنی‌های گردی باشند. نمودارهای توابع چندجمله‌ای هم پیوسته و هم هموار هستند. یک چندجمله‌ای درجه $$n$$ حداکثر $$n$$ طول از مبداء و $$n - 1$$ نقطه برگشت دارد.

مثال ۱۰: بدون رسم منحنی تابع، رفتار محلی تابع $$f(x)=−3x^{10}+4x^7−x^4+2x^3$$ را با یافتن حداکثر تعداد طول از مبداءها و نقاط برگشت تعیین کنید.

پاسخ: درجه چندجمله‌ای ۱۰ است، بنابراین، حداکثر $$n$$ برخورد با محور $$x$$ و حداکثر $$n - 1$$ نقطه برگشت وجود دارد.

مثال ۱۱: درباره چندجمله‌ای نشان داده شده در شکل ۱۲ بر اساس تقاطع‌ها و نقاط برگشت آن چه نتیجه‌ای می‌توانیم بگیریم؟

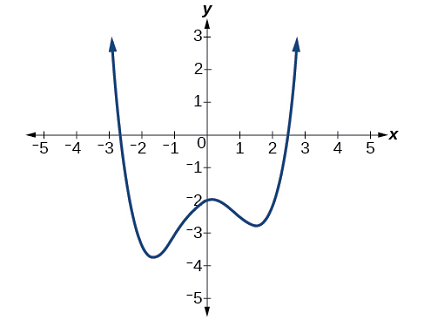
پاسخ: رفتار حدی نمودار به ما می‌گوید که نمودار مربوط به یک چندجمله‌ای درجه زوج است. شکل ۱۳ را ببینید.

نمودار دو طول از مبداء دارد که مرتبه ۲ یا بزرگ‌تر را نشان می‌دهد و ۳ نقطه بازگشت نیز درجه ۴ یا بزرگ‌تر را نشان می‌دهد. بر اساس این موضوع، منطقی خواهد بود که نتیجه بگیریم درجه زوج و حداقل برابر با ۴ است.

مثال ۱۲: رفتار محلی تابع $$f(x)=−4x(x+3)(x−4)$$ را بررسی کنید.

پاسخ: عرض از مبداء با $$f ( 0 )$$ به دست می‌آید.

$$\large \begin{align} f(0)&=−4(0)(0+3)(0−4) \\ &=0 \end{align}$$

عرض از مبداء نقطه $$( 0 , 0 )$$ است.

طول از مبداء را می‌توان با تعیین صفرهای تابع پیدا کرد:

$$\large \begin{align} 0&=-4x(x+3)(x-4) \\ x&=0 & &\text{or} & x+3&=0 & &\text{or} & x-4&=0 \\ x&=0 & &\text{or} & x&=−3 & &\text{or} & x&=4 \end{align}$$

در نتیجه، عرض از مبداءها، نقاط $$( 0 , 0 )$$، $$( - 3 , 0 )$$ و $$( 4 , 0 )$$ است. تابع نیز درجه ۳ است، زیرا نمودار حداکثر ۲ نقطه بازگشت دارد.