در آموزشهای قبلی مجله فرادرس ، درباره انتگرال و روشهای محاسبه آن بحث کردیم. در این آموزشها، مباحثی مانند انتگرال توابع مثلثاتی ، انتگرالگیری جزء به جزء و انتگرال دوگانه را معرفی کردیم. همچنین با انتگرال سه گانه آشنا شدیم و مطالب انتگرال سه گانه در مختصات کروی ، انتگرال سه گانه در مختصات استوانهای و تغییر متغیر در انتگرال سه گانه را بیان کردیم. انتگرال سه گانه در مباحث مختلف فیزیک کاربرد فراوانی دارد. در این آموزش، چند مورد از مهمترین کاربردهای انتگرال سه گانه در فیزیک را بررسی میکنیم.
جرم و گشتاورهای ایستای جسم صلب
فرض کنید یک جسم صلب فضای U U U M ( x , y , z ) M\left( {x,y,z} \right) M ( x , y , z ) ρ ( x , y , z ) \rho\left( {x,y,z} \right) ρ ( x , y , z ) m m m
m = ∭ U ρ ( x , y , z ) d x d y d z . \large m = \iiint \limits _ U {\rho \left ( { x ,y , z } \right ) d x dy d z } . m = U ∭ ρ ( x , y , z ) d x d y d z .
برای به دست آوردن گشتاورهای ایستای جسم حول صفحات مختصات O x y Oxy O x y O x z Oxz O x z O y z Oyz O yz
M x y = ∫ U z ρ ( x , y , z ) d x d y d z , \large {{M_{xy}} = \int\limits_U {z\rho \left( {x,y,z} \right)dxdydz} , \;\;} M x y = U ∫ z ρ ( x , y , z ) d x d y d z ,
M y z = ∫ U x ρ ( x , y , z ) d x d y d z , \large {{M_{yz}} = \int\limits_U {x\rho \left( {x,y,z} \right)dxdydz} ,\;\;} M yz = U ∫ x ρ ( x , y , z ) d x d y d z ,
M x z = ∫ U y ρ ( x , y , z ) d x d y d z . \large {{M_{xz}} = \int\limits_U {y\rho \left( {x,y,z} \right)dxdydz} .} M x z = U ∫ y ρ ( x , y , z ) d x d y d z .
مختصات مرکز ثقل جسم صلب را میتوان با استفاده عبارات زیر تعیین کرد:
x ˉ = M y z m = ∭ U x ρ ( x , y , z ) d x d y d z ∭ U ρ ( x , y , z ) d x d y d z , y ˉ = M x z m = ∭ U y ρ ( x , y , z ) d x d y d z ∭ U ρ ( x , y , z ) d x d y d z , z ˉ = M x y m = ∭ U z ρ ( x , y , z ) d x d y d z ∭ U ρ ( x , y , z ) d x d y d z . \large { { \bar x = \frac { { { M _ {y z }} } } {m } } = { \frac { { \iiint \limits _ U { x \rho \left ( { x , y, z } \right ) d x dy d z } } } { { \iiint \limits _ U { \rho \left ( { x, y , z } \right ) dx d y d z} }} , \; \; } } \kern-0.3pt \\ \large { { \bar y = \frac { { { M _ { xz } }} } { m } } = { \frac { { \iiint \limits _ U { y \rho \left ( { x , y, z } \right ) d x d y d z } } } { { \iiint \limits _ U { \rho \left ( { x , y , z } \right ) d x d y dz } } } , \; \; } } \kern-0.3pt \\ \large { { \bar z = \frac { {{ M _ { x y } } } } { m} } = { \frac { { \iiint \limits _ U { z \rho \left ( { x , y , z } \right ) d xd y d z } } } { { \iiint \limits _ U { \rho \left ( { x , y , z } \right )d x d y d z } } } . } } x ˉ = m M yz = U ∭ ρ ( x , y , z ) d x d y d z U ∭ x ρ ( x , y , z ) d x d y d z , y ˉ = m M x z = U ∭ ρ ( x , y , z ) d x d y d z U ∭ y ρ ( x , y , z ) d x d y d z , z ˉ = m M x y = U ∭ ρ ( x , y , z ) d x d y d z U ∭ z ρ ( x , y , z ) d x d y d z .
اگر جسم به ازای چگالی ρ ( x , y , z ) = 1 {\rho \left( {x,y,z} \right)} = 1 ρ ( x , y , z ) = 1 M ( x , y , z ) {M\left( {x,y,z} \right)} M ( x , y , z ) U U U
گشتاورهای لختی جسم صلب
گشتاورهای لختی یک جسم صلب حول صفحات مختصات O x y Oxy O x y O x z Oxz O x z O y z Oyz O yz
I x y = ∭ U z 2 ρ ( x , y , z ) d x d y d z , I y z = ∭ U x 2 ρ ( x , y , z ) d x d y d z , I x z = ∭ U y 2 ρ ( x , y , z ) d x d y d z \large { { { I _ { xy } } } = { \iiint \limits _ U { { z ^ 2 } \rho \left ( { x , y , z } \right ) d x d y d z } , \; \; } } \kern-0.3pt \\ \large { { { I _ { y z } } } = { \iiint \limits _ U { { x ^ 2 } \rho \left ( { x , y, z } \right ) d x d y d z } , \; \; } } \kern -0.3pt \\ \large { { { I _ { x z } } } = { \iiint \limits _ U { { y ^ 2 } \rho \left ( { x , y , z } \right ) d x d y dz } } } I x y = U ∭ z 2 ρ ( x , y , z ) d x d y d z , I yz = U ∭ x 2 ρ ( x , y , z ) d x d y d z , I x z = U ∭ y 2 ρ ( x , y , z ) d x d y d z
و گشتاورهای لختی جسم حول محورهای مختصات O x Ox O x O y Oy O y O z Oz O z
I x = ∭ U ( y 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z , I y = ∭ U ( x 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z , I z = ∭ U ( x 2 + y 2 ) ⋅ ρ ( x , y , z ) d x d y d z . \large { { { I _ x } = \iiint \limits _ U { \left ( { { y ^ 2 } + { z ^ 2 } } \right ) \cdot } } \kern0pt { { \rho \left ( { x , y , z } \right ) d x d y d z } ,\;\;}}\kern-0.3pt \\ \large { { { I _y } = \iiint \limits _ U { \left ( { { x ^ 2 } + { z ^ 2 } } \right ) \cdot } } \kern0pt { {\rho \left( { x ,y , z } \right) d x d y d z } ,\;\;}}\kern-0.3pt \\ \large {{{I_z} = \iiint\limits_U {\left( {{x^2} + {y^2}} \right ) \cdot}}\kern0pt{ { \rho \left ( { x , y, z } \right ) d x dy d z } .\;\;}}\kern-0.3pt I x = U ∭ ( y 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z , I y = U ∭ ( x 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z , I z = U ∭ ( x 2 + y 2 ) ⋅ ρ ( x , y , z ) d x d y d z .
همانگونه که مشاهده میکنیم، این گشتاورها دارای ویژگیهایی به صورت زیر هستند:
I x = I x y + I x z , I y = I x y + I y z , I z = I x z + I y z . \large { { I _ x } = { I _ { x y } } + { I _ { x z } } ,\;\;}\kern-0.3pt { { I _ y } = { I _ { x y } } + { I _ { y z} } , \;\;}\kern-0.3pt {{ I _ z } = { I _ { x z } } + { I _ { y z } } . } I x = I x y + I x z , I y = I x y + I yz , I z = I x z + I yz .
برای به دست آوردن گشتاور لختی حول مبدأ باید انتگرال زیر را محاسبه کنیم:
I 0 = ∭ U ( x 2 + y 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z . \large { I _ 0 } = \iiint \limits _ U { \left ( { { x ^ 2 } + { y ^ 2 } + { z ^ 2 } } \right ) } \cdot \kern 0pt { \rho \left ( { x , y , z } \right ) d x d y dz } . I 0 = U ∭ ( x 2 + y 2 + z 2 ) ⋅ ρ ( x , y , z ) d x d y d z .
گشتاور لختی حول مبدأ را میتوان از طریق گشتاورهای لختی حول صفحات مختصات نیز به دست آورد:
I 0 = I x y + I y z + I x z . \large { I _ 0 } = { I _ { x y } } + { I _ { y z } } + { I _ { x z } } . I 0 = I x y + I yz + I x z .
تانسور لختی
با استفاده از گشتاورهای I x I_x I x I y I_y I y I z I_z I z I x y I_{xy} I x y I x z I_{xz} I x z I y z I_{yz} I yz تانسور لختی یک جسم صلب را به صورت زیر به دست آوریم:
$$ \large { I } = { \left ( { \begin {array} { * { 2 0 } { c } }<br />
{ { I _ x } } & { – { I _ { x y } } } & { – { I _{ x z } } } \\<br />
{ – { I _ { x y } } } & {{ I _ y } } & { – { I _ { y z} } } \\<br />
{ – { I _ { x z }} } & { – { I _ { y z }} } & { { I _ z } }<br />
\end {array} } \right ) .} $$
این تانسور متقارن است و از این رو میتوان با انتخاب محورهای مختصات مناسب O x ’ Ox’ O x ’ O y ’ Oy’ O y ’ O z ’ Oz’ O z ’
اگر جسمی حول محوری دوران کند که بر محور لختی اصلی منطبق نباشد، در سرعتهای چرخشی بالا لرزشهایی به وجود خواهد آمد. بنابراین، هنگام طراحی لازم است محور دوران بر یکی از محورهای لختی اصلی منطبق باشد. برای مثال، در تعویض لاستیکهای ماشین، برای تعادل چرخها اغلب لازم است قطعههای سربی کوچکی به آنها وصل شود؛ زیرا با این کار محور دوران و محور لختی اصلی بر هم منطبق میشوند و لرزش از بین میرود.
پتانسیل گرانشی و نیروی جاذبه
پتانسیل نیوتنی یک جسم در نقطه P ( x , y , z ) P\left( {x,y,z} \right) P ( x , y , z )
u ( x , y , z ) = ∭ U ρ ( ξ , η , ζ ) d ξ d η d ζ r \large { u \left( { x , y , z } \right ) \text { = } } \kern0pt { \iiint \limits _ U { \rho \left ( { \xi ,\eta ,\zeta } \right ) \frac { { d \xi d \eta d \zeta } } { r } } } u ( x , y , z ) = U ∭ ρ ( ξ , η , ζ ) r d ξ d η d ζ
که در آن، ρ ( ξ , η , ζ ) {\rho \left( {\xi ,\eta ,\zeta } \right)} ρ ( ξ , η , ζ )
r = ( ξ – x ) 2 + ( η – y ) 2 + ( ζ – z ) 2 \large { r \text { = } } \kern0pt { \sqrt { { { \left ( { \xi – x } \right ) } ^ 2 } + { { \left ( { \eta – y } \right ) } ^ 2 } + { { \left ( { \zeta – z } \right ) } ^ 2 } } } r = ( ξ – x ) 2 + ( η – y ) 2 + ( ζ – z ) 2
در اینجا انتگرالگیری روی کل حجم جسم انجام میشود. با به دست آوردن پتانسیل، میتوان نیروی جاذبه نقطهای به جرم m m m ρ ( ξ , η , ζ ) {\rho \left( {\xi ,\eta ,\zeta } \right)} ρ ( ξ , η , ζ )
F = – G m grad u \large \mathbf { F } = – G m \, \mathbf { \text {grad} } \, u F = – G m grad u
که در آن، G G G
مثالها
در ادامه، چند مثال حل شده مربوط به موضوعات بالا را بررسی میکنیم.
مثال ۱
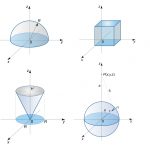
مرکز جرم یک نیمکره توپر همگن به شعاع R R R
حل: دستگاه مختصات را به گونهای در نظر میگیریم که نیمکره در z ≥ 0 z \ge 0 z ≥ 0
شکل ۱ با استفاده از این دستگاه مختصات، میتوان مرکز جرم (مرکز ثقل) این نیمکره را به دست آورد. مطابق با تقارنی که در شکل 1 وجود دارد، رابطه زیر بدیهی است:
x ˉ = y ˉ = 0. \large \bar x = \bar y = 0. x ˉ = y ˉ = 0.
مشخصه z ˉ \bar z z ˉ
z ˉ = M x y m = ∭ U z ρ ( x , y , z ) d x d y d z ∭ U ρ ( x , y , z ) d x d y d z . \large { \bar z = \frac { { { M _ { x y } } } } { m } } = { \frac { { \iiint \limits _ U { z \rho \left ( { x , y , z } \right ) d x d y d z } } } { { \iiint \limits _ U { \rho \left ( { x , y , z } \right ) d x d y d z } } } . } z ˉ = m M x y = U ∭ ρ ( x , y , z ) d x d y d z U ∭ z ρ ( x , y , z ) d x d y d z .
از آنجایی که نیمکره همگن است، ρ ( x , y , z ) = ρ 0 \rho \left( {x,y,z} \right) = {\rho _0} ρ ( x , y , z ) = ρ 0
$$ \large \require {cancel}<br />
{ \bar z = \frac { { { \bcancel { \rho _ 0 } } \iiint \limits _ U { z d x d y d z} } } { { { \bcancel { \rho _ 0 } } \iiint \limits _ U { d xd y d z } } } }<br />
= { \frac { { \iiint \limits _ U { z d xd y d z } } } { { \iiint \limits _ U { d x d y dz } } } }<br />
= { \frac { { \iiint \limits _ U { z d x d yd z } } } { V } . } $$
نماد V V V
V = 1 2 ( 4 3 π R 3 ) = 2 3 π R 3 . \large { V = \frac { 1 } { 2 } \left ( { \frac {4 }{ 3 } \pi { R ^ 3 } } \right ) } = { \frac { 2 } {3 } \pi { R ^ 3 } . } V = 2 1 ( 3 4 π R 3 ) = 3 2 π R 3 .
اکنون باید انتگرال سه گانه ∭ U z d x d y d z {\iiint\limits_U {zdxdydz} } U ∭ z d x d y d z مختصات کروی استفاده میکنیم. در نتیجه خواهیم داشت:
∭ U z d x d y d z = ∭ U ’ r cos θ r 2 sin θ d r d φ d θ = ∫ 0 2 π d φ ∫ 0 R r 3 d r ∫ 0 π 2 cos θ sin θ d θ = ∫ 0 2 π d φ ∫ 0 R r 3 d r ∫ 0 π 2 sin θ d ( sin θ ) = ∫ 0 2 π d φ ∫ 0 R r 3 d r ⋅ [ ( sin 2 θ 2 ) ∣ θ = 0 θ = π 2 ] = ∫ 0 2 π d φ ∫ 0 R r 3 d r ⋅ 1 2 = 1 2 ∫ 0 2 π d φ ⋅ [ ( r 4 4 ) ∣ 0 R ] = R 4 8 ∫ 0 2 π d φ = R 4 8 ⋅ 2 π = π R 4 4 . \large { \iiint \limits _ U { z dx d y d z } } = {\iiint\limits_{U’} {r\cos \theta {r^2}\sin \theta drd\varphi d\theta } } \\ \large = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos \theta \sin \theta d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin \theta d\left( {\sin \theta } \right)} } \\ \large = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot}\kern0pt{ \left[ {\left. {\left( {\frac{{{{\sin }^2}\theta }}{2}} \right)} \right|_{\theta = 0}^{\theta = \large\frac{\pi }{2}\normalsize}} \right] } \\ \large = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot \frac{1}{2} = \frac{1}{2}\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^R} \right] } \\ \large = {\frac{{{R^4}}}{8}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{{R^4}}}{8} \cdot 2\pi } = {\frac{{\pi {R^4}}}{4}.} U ∭ z d x d y d z = U ’ ∭ r cos θ r 2 sin θ d r d φ d θ = 0 ∫ 2 π d φ 0 ∫ R r 3 d r 0 ∫ 2 π cos θ sin θ d θ = 0 ∫ 2 π d φ 0 ∫ R r 3 d r 0 ∫ 2 π sin θ d ( sin θ ) = 0 ∫ 2 π d φ 0 ∫ R r 3 d r ⋅ ( 2 sin 2 θ ) θ = 0 θ = 2 π = 0 ∫ 2 π d φ 0 ∫ R r 3 d r ⋅ 2 1 = 2 1 0 ∫ 2 π d φ ⋅ ( 4 r 4 ) 0 R = 8 R 4 0 ∫ 2 π d φ = 8 R 4 ⋅ 2 π = 4 π R 4 .
بنابراین، مختصه z ˉ \bar z z ˉ
z ˉ = ∭ U z d x d y d z V = 1 4 π R 4 2 4 π R 3 = 3 R 8 . \large { \bar z = \frac { { \iiint \limits _ U { z d x d y dz } } } { V } } = { \frac { { \frac { 1 }{ 4 } \pi { R ^ 4 } } } { { \frac { 2 } { 4 } \pi { R ^ 3 } } } } = { \frac { { 3 R } } {8 } . } z ˉ = V U ∭ z d x d y d z = 4 2 π R 3 4 1 π R 4 = 8 3 R .
مثال 2
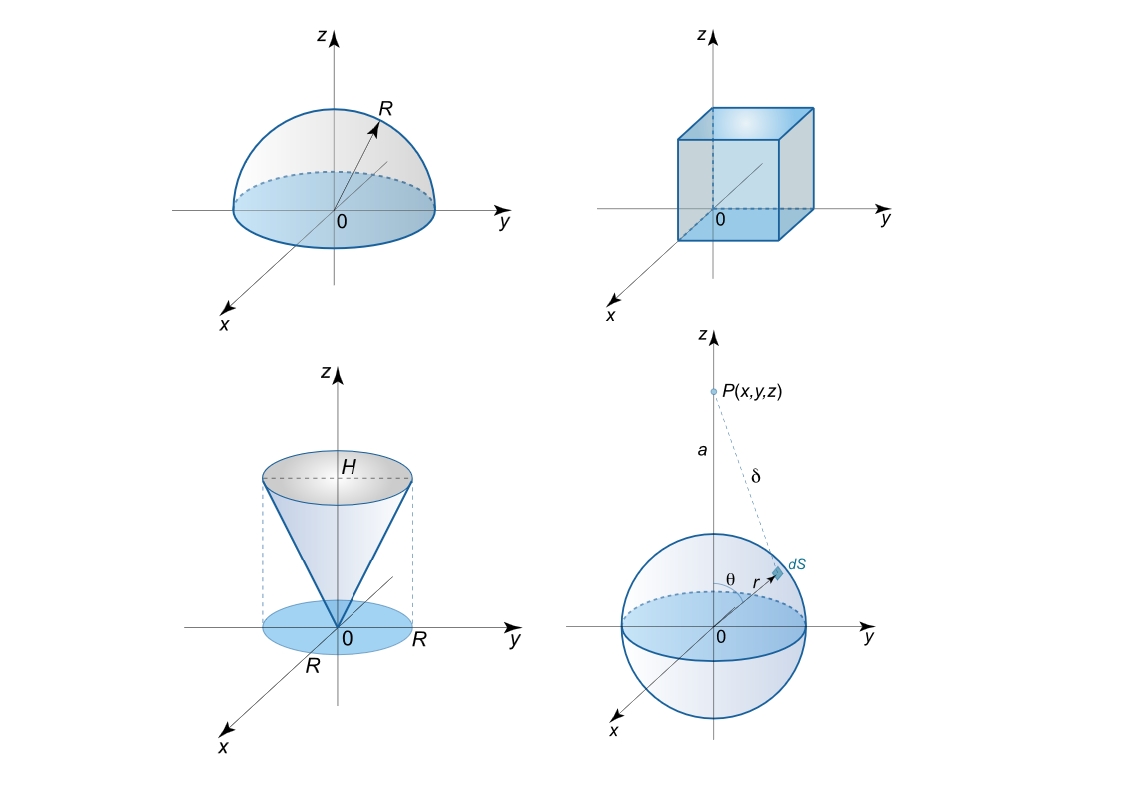
جرم و مختصات مرکز ثقل یک مکعب واحد با چگالی ρ ( x , y , z ) = x + 2 y + 3 z \rho \left( {x,y,z} \right) =x + 2y + 3z ρ ( x , y , z ) = x + 2 y + 3 z
شکل ۲ حل: ابتدا جرم مکعب را محاسبه میکنیم:
m = ∭ U ρ ( x , y , z ) d x d y d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 ( x + 2 y + 3 z ) d z = ∫ 0 1 d x ∫ 0 1 d y ⋅ [ ( x z + 2 y z + 3 z 2 2 ) ∣ z = 0 z = 1 ] = ∫ 0 1 d x ∫ 0 1 ( x + 2 y + 3 2 ) d y = ∫ 0 1 d x ⋅ [ ( x y + y 2 + 3 2 y ) ∣ y = 0 y = 1 ] = ∫ 0 1 ( x + 1 + 3 2 ) d x = ∫ 0 1 ( x + 5 2 ) d x = ( x 2 2 + 5 2 x ) ∣ 0 1 = 1 2 + 5 2 = 3. \large { m }={ \iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} } = {\int\limits _ 0 ^ 1 {dx} \int\limits _ 0 ^ 1 { d y } \int\limits_0^1 {\left( {x + 2y + 3z} \right)dz} } \\ \large = {\int\limits _ 0 ^ 1 {d x } \int \limits _ 0 ^ 1 { d y } \cdot}\kern0pt{ \left[ {\left. {\left( {xz + 2yz + \frac{{3{z^2}}}{2}} \right)} \right| _ { z = 0 } ^ { z = 1 } } \right] } = {\int\limits _ 0 ^ 1 {dx} \int\limits _ 0 ^ 1 {\left( {x + 2y + \frac{3}{2}} \right)dy} } \\ \large = {\int\limits_0^1 {dx} \cdot}\kern0pt{ \left[ {\left. {\left( {xy + {y ^ 2} + \frac{3}{2}y} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\int \limits _ 0 ^ 1 {\left( {x + 1 + \frac{3}{2}} \right)dx} } \\ \large = {\int\limits _ 0 ^ 1 {\left( {x + \frac{5}{2}} \right)dx} } = {\left. {\left( {\frac { { { x ^ 2 } } } { 2 } + \frac{5}{2}x} \right)} \right| _ 0 ^ 1 } = {\frac { 1 } { 2 } + \frac { 5 } { 2 } }={ 3.} m = U ∭ ρ ( x , y , z ) d x d y d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 ( x + 2 y + 3 z ) d z = 0 ∫ 1 d x 0 ∫ 1 d y ⋅ ( x z + 2 yz + 2 3 z 2 ) z = 0 z = 1 = 0 ∫ 1 d x 0 ∫ 1 ( x + 2 y + 2 3 ) d y = 0 ∫ 1 d x ⋅ [ ( x y + y 2 + 2 3 y ) y = 0 y = 1 ] = 0 ∫ 1 ( x + 1 + 2 3 ) d x = 0 ∫ 1 ( x + 2 5 ) d x = ( 2 x 2 + 2 5 x ) 0 1 = 2 1 + 2 5 = 3.
اکنون گشتاورهای ایستای M x y M_{xy} M x y M x z M_{xz} M x z M y z M_{yz} M yz
M x y = ∭ U z ρ ( x , y , z ) d x d y d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 z ( x + 2 y + 3 z ) d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 ( x z + 2 z y + 3 z 2 ) d z = ∫ 0 1 d x ∫ 0 1 d y ⋅ [ ( ( x + 2 y ) z 2 2 + z 3 ) ∣ z = 0 z = 1 ] = ∫ 0 1 d x ∫ 0 1 ( 1 2 ( x + 2 y ) + 1 ) d y = 1 2 ∫ 0 1 d x ∫ 0 1 ( x + 2 y + 2 ) d y = 1 2 ∫ 0 1 d x ⋅ [ ( x y + y 2 + 2 y ) ∣ y = 0 y = 1 ] = 1 2 ∫ 0 1 ( x + 3 ) d x = 1 2 [ ( x 2 2 + 3 x ) ∣ 0 1 ] = 1 2 ( 1 2 + 3 ) = 7 4 . \large { { M _ { x y } } } = { \iiint\limits_U {z\rho \left( {x,y,z} \right) d x d y d z} } = { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ 1 { d y} \int \limits _ 0 ^ 1 { z \left ( {x + 2y + 3 z } \right ) d z} } \\ \large = {\int\limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ 1 { d y } \int \limits _ 0 ^ 1 { \left ( { x z + 2 z y + 3 { z ^ 2 } } \right ) dz } } = { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^1 { d y} \cdot } \kern0pt{ \left[ {\left. {\left ( {\left( { x + 2 y } \right ) \frac { { { z ^ 2 } }} {2 } + { z ^ 3 } } \right ) } \right | _ { z = 0 } ^ { z = 1 } } \right ] } \\ \large = {\int\limits_0 ^ 1 {dx} \int\limits_0^1 {\left( {\frac{1}{2}\left( {x + 2y} \right) + 1} \right)dy} } = {\frac{1}{2}\int\limits_0^1 {dx} \int\limits _0 ^ 1 {\left( {x + 2y + 2} \right) d y} } \\ \large = {\frac{1}{2}\int\limits _ 0 ^ 1 { d x} \cdot}\kern0pt{ \left[ {\left. {\left( {xy + {y^2} + 2y} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\frac { 1 } { 2 } \int \limits _ 0 ^ 1 { \left ( { x + 3 } \right ) d x } } = { \frac { 1 } { 2 }\left[ {\left. {\left( {\frac{{{x^2}}}{2} + 3x} \right)} \right | _ 0 ^ 1 } \right] } \\ = {\frac { 1 } { 2 } \left( { \frac { 1} {2 } + 3 } \right ) } = { \frac {7 }{ 4 } .} M x y = U ∭ z ρ ( x , y , z ) d x d y d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 z ( x + 2 y + 3 z ) d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 ( x z + 2 zy + 3 z 2 ) d z = 0 ∫ 1 d x 0 ∫ 1 d y ⋅ ( ( x + 2 y ) 2 z 2 + z 3 ) z = 0 z = 1 = 0 ∫ 1 d x 0 ∫ 1 ( 2 1 ( x + 2 y ) + 1 ) d y = 2 1 0 ∫ 1 d x 0 ∫ 1 ( x + 2 y + 2 ) d y = 2 1 0 ∫ 1 d x ⋅ [ ( x y + y 2 + 2 y ) y = 0 y = 1 ] = 2 1 0 ∫ 1 ( x + 3 ) d x = 2 1 ( 2 x 2 + 3 x ) 0 1 = 2 1 ( 2 1 + 3 ) = 4 7 .
به طور مشابه، برای گشتاورهای M x z M_{xz} M x z M y z M_{yz} M yz
M x z = ∭ U y ρ ( x , y , z ) d x d y d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 y ( x + 2 y + 3 z ) d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 ( y x + 2 y 2 + 3 y z ) d z = ∫ 0 1 d x ∫ 0 1 d y ⋅ [ ( y x z + 2 y 2 z + 3 y z 2 2 ) ∣ z = 0 z = 1 ] = ∫ 0 1 d x ∫ 0 1 ( y x + 2 y 2 + 3 y 2 ) d y = ∫ 0 1 d x ⋅ [ ( x y 2 2 + 2 y 3 3 + 3 y 2 4 ) ∣ y = 0 y = 1 ] = ∫ 0 1 ( x 2 + 2 3 + 3 4 ) d x = ∫ 0 1 ( x 2 + 17 12 ) d x = ( x 2 4 + 17 x 12 ) ∣ 0 1 = 1 4 + 17 12 = 20 12 = 5 3 . \large { { M _ { x z }} } = { \iiint \limits _ U { y \rho \left( { x , y, z } \right)dxdydz} } = {\int\limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ 1 { d y } \int \limits _ 0 ^ 1 {y\left( {x + 2y + 3z} \right)dz} } \\ \large = {\int\limits _ 0 ^1 { d x } \int \limits _ 0 ^ 1 { d y } \int \limits _ 0 ^ 1 { \left ( { y x + 2 { y ^ 2 } + 3y z } \right ) d z } } = {\int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ 1 { d y } \cdot } \kern0pt { \left [ { \left. { \left ( { y x z + 2 { y ^ 2 } z + \frac {{ 3 y { z ^ 2 } } } {2 } } \right)} \right|_{z = 0}^{z = 1}} \right] } \\ \large = {\int\limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ 1 {\left( { y x + 2{ y ^ 2 } + \frac { { 3 y } } {2 } } \right ) d y } } = {{\int\limits _ 0 ^ 1 { d x } \cdot } \kern0pt { \left[ {\left. {\left( {\frac{{x{y^2}}}{2} + \frac{{2{y^3}}}{3} + \frac{{3{y^2}}}{4}} \right)} \right|_{y = 0}^{y = 1}} \right] }} \\ \large = {\int\limits_0^1 {\left( {\frac{x}{2} + \frac{2}{3} + \frac{3}{4}} \right)dx} } = {\int\limits_0^1 {\left( {\frac{x}{2} + \frac{{17}}{{12}}} \right)dx} } = {\left. {\left( {\frac { { {x ^ 2 }} } { 4} + \frac{{17x}}{{12}}} \right)} \right|_0^1 } \\ \large = {\frac{1}{4} + \frac { {1 7 } } {{ 12 } } } = {\frac{{20}}{{12}} }={ \frac{5}{3}.} M x z = U ∭ y ρ ( x , y , z ) d x d y d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 y ( x + 2 y + 3 z ) d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 ( y x + 2 y 2 + 3 yz ) d z = 0 ∫ 1 d x 0 ∫ 1 d y ⋅ ( y x z + 2 y 2 z + 2 3 y z 2 ) z = 0 z = 1 = 0 ∫ 1 d x 0 ∫ 1 ( y x + 2 y 2 + 2 3 y ) d y = 0 ∫ 1 d x ⋅ ( 2 x y 2 + 3 2 y 3 + 4 3 y 2 ) y = 0 y = 1 = 0 ∫ 1 ( 2 x + 3 2 + 4 3 ) d x = 0 ∫ 1 ( 2 x + 12 17 ) d x = ( 4 x 2 + 12 17 x ) 0 1 = 4 1 + 12 17 = 12 20 = 3 5 .
و
M y z = ∭ U x ρ ( x , y , z ) d x d y d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 x ( x + 2 y + 3 z ) d z = ∫ 0 1 d x ∫ 0 1 d y ∫ 0 1 ( x 2 + 2 x y + 3 x z ) d z = ∫ 0 1 d x ∫ 0 1 d y ⋅ [ ( x 2 z + 2 x y z + 3 x z 2 2 ) ∣ z = 0 z = 1 ] = ∫ 0 1 d x ∫ 0 1 ( x 2 + 2 x y + 3 x 2 ) d y = ∫ 0 1 d x ⋅ [ ( x 2 y + x y 2 + 3 x y 2 ) ∣ y = 0 y = 1 ] = ∫ 0 1 ( x 2 + x + 3 x 2 ) d x = ∫ 0 1 ( x 2 + 5 x 2 ) d x = ( x 3 3 + 5 x 2 4 ) ∣ 0 1 = 1 3 + 5 4 = 19 12 . \large {{ M _ {y z } } } = { \iiint\limits _ U { x \rho \left ( { x , y ,z } \right)dxdydz} } = { \int \limits _ 0 ^ 1 { d x } \int\limits_0^1 {dy} \int\limits _ 0 ^ 1 { x\left( {x + 2y + 3z} \right)dz} } \\ \large = {\int\limits _ 0 ^ 1 { d x } \int\limits _ 0 ^ 1 {d y} \int\limits_0^1 {\left( {{ x ^ 2 } + 2xy + 3xz} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \cdot}\kern0pt{ \left[ {\left. {\left( {{x^2}z + 2xyz + \frac{{3x{z^2}}}{2}} \right)} \right|_{z = 0}^{z = 1}} \right] } \\ \large = {\int\limits_0^1 {dx} \int\limits_0^1 {\left( {{x^2} + 2xy + \frac{{3x}}{2}} \right)dy} } = {\int\limits_0^1 {dx} \cdot}\kern0pt{ \left[ {\left. {\left( {{x^2}y + x{y^2} + \frac{{3xy}}{2}} \right)} \right|_{y = 0}^{y = 1}} \right] } \\ \large = {\int\limits_0^1 {\left( {{x^2} + x + \frac{{3x}}{2}} \right)dx} } = {\int\limits_0^1 {\left( {{x^2} + \frac{{5x}}{2}} \right)dx} } = {\left. {\left( {\frac{{{x^3}}}{3} + \frac{{5{x^2}}}{4}} \right)} \right|_0^1 } \\ \large = {\frac{1}{3} + \frac{5}{4} }={ \frac{{19}}{{12}}.} M yz = U ∭ x ρ ( x , y , z ) d x d y d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 x ( x + 2 y + 3 z ) d z = 0 ∫ 1 d x 0 ∫ 1 d y 0 ∫ 1 ( x 2 + 2 x y + 3 x z ) d z = 0 ∫ 1 d x 0 ∫ 1 d y ⋅ ( x 2 z + 2 x yz + 2 3 x z 2 ) z = 0 z = 1 = 0 ∫ 1 d x 0 ∫ 1 ( x 2 + 2 x y + 2 3 x ) d y = 0 ∫ 1 d x ⋅ [ ( x 2 y + x y 2 + 2 3 x y ) y = 0 y = 1 ] = 0 ∫ 1 ( x 2 + x + 2 3 x ) d x = 0 ∫ 1 ( x 2 + 2 5 x ) d x = ( 3 x 3 + 4 5 x 2 ) 0 1 = 3 1 + 4 5 = 12 19 .
در نتیجه، مختصات مرکز ثقل مکعب به صورت زیر است:
x ˉ = M y z m = 19 12 3 = 19 36 , y ˉ = M x z m = 5 3 3 = 5 9 = 20 36 , z ˉ = M x y m = 7 4 3 = 7 12 = 21 36 . \large {\bar x = \frac { { { M _{ y z} } } } { m } = \frac { { \frac { {1 9 }} { { 12 } } }} {3 } = \frac { {1 9 }} { { 3 6 } },\;\;\;}\kern-0.3pt \\ \large {\bar y = \frac { { { M _ { xz } } }} { m } = \frac{{\frac{5}{3}}}{3} = \frac { 5 }{ 9 } = \frac{{20}}{{36}},\;\;\;}\kern-0.3pt \\ \large {\bar z = \frac { { {M _ {x y } } } } {m } = \frac { { \frac { 7 } { 4 }} } {3 } = \frac { 7 } { {1 2 } } = \frac { { 21 } } {{3 6 } } .} x ˉ = m M yz = 3 12 19 = 36 19 , y ˉ = m M x z = 3 3 5 = 9 5 = 36 20 , z ˉ = m M x y = 3 4 7 = 12 7 = 36 21 .
مثال ۳
جرم یک کره توپر با شعاع R R R γ \gamma γ
حل: طبق شرط مسئله، چگالی γ \gamma γ γ = a r 2 \gamma = a{r^2} γ = a r 2 a a a r r r
m = ∭ U γ ( r , φ , θ ) r 2 sin θ d r d φ d θ = ∭ U a r 2 r 2 sin θ d r d φ d θ = a ∭ U r 4 sin θ d r d φ d θ = a ∫ 0 2 π d φ ∫ 0 R r 4 d r ∫ 0 π sin θ d θ = a ∫ 0 2 π d φ ∫ 0 R r 4 d r ⋅ [ ( – cos θ ) ∣ 0 π ] = a ∫ 0 2 π d φ ∫ 0 R r 4 d r ⋅ ( – cos π + cos 0 ) = 2 a ∫ 0 2 π d φ ∫ 0 R r 4 d r = 2 a ∫ 0 2 π d φ ⋅ [ ( r 5 5 ) ∣ 0 R ] = 2 a R 5 5 ∫ 0 2 π d φ = 2 a R 5 5 ⋅ 2 π = 4 a π R 5 5 . \large { m \text{ = }}\kern0pt{ \iiint\limits_U {\gamma \left( {r,\varphi ,\theta } \right){r^2}\sin \theta drd\varphi d\theta } } = {\iiint\limits_U { a { r^ 2 } { r ^ 2 }\sin \theta drd\varphi d\theta } }\\ \large = {a\iiint\limits _ U { { r ^ 4 }\sin \theta drd \varphi d\theta } } = {a\int\limits_0^{2\pi } {d\varphi } \int\limits _ 0 ^ R {{r ^ 4 }d r} \int\limits_0^\pi {\sin \theta d\theta } }\\ \large = { a \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ R { { r ^ 4 } d r } \cdot \left[ {\left. {\left( { – \cos \theta } \right)} \right | _ 0 ^ \pi } \right] } = {a\int\limits _ 0 ^ { 2 \pi } { d \varphi } \int\limits_0^R { { r ^ 4 } d r } \cdot}\kern0pt{ \left ( { – \cos \pi + \cos 0} \right) } \\ \large = { 2 a \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ R { { r ^ 4 } d r } } = { 2 a \int \limits _ 0 ^ { 2 \pi } { d \varphi } \cdot \left[ {\left. {\left( {\frac { {{ r ^ 5 } } } { 5 } } \right ) } \right | _ 0 ^ R } \right] } \\ \large = {\frac { {2 a { R ^ 5 }} } { 5 } \int \limits _ 0 ^ { 2 \pi } { d \varphi } } = { \frac { { 2 a{ R ^ 5 } } } { 5 } \cdot 2 \pi } = { \frac { { 4 a \pi { R ^5 } }} { 5} . } m = U ∭ γ ( r , φ , θ ) r 2 sin θ d r d φ d θ = U ∭ a r 2 r 2 sin θ d r d φ d θ = a U ∭ r 4 sin θ d r d φ d θ = a 0 ∫ 2 π d φ 0 ∫ R r 4 d r 0 ∫ π sin θ d θ = a 0 ∫ 2 π d φ 0 ∫ R r 4 d r ⋅ [ ( – cos θ ) ∣ 0 π ] = a 0 ∫ 2 π d φ 0 ∫ R r 4 d r ⋅ ( – cos π + cos 0 ) = 2 a 0 ∫ 2 π d φ 0 ∫ R r 4 d r = 2 a 0 ∫ 2 π d φ ⋅ ( 5 r 5 ) 0 R = 5 2 a R 5 0 ∫ 2 π d φ = 5 2 a R 5 ⋅ 2 π = 5 4 aπ R 5 .
مثال 4
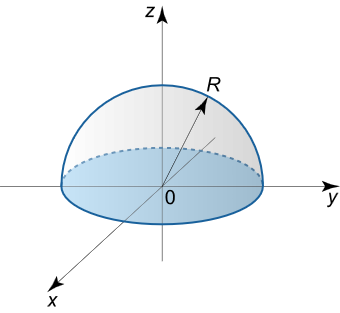
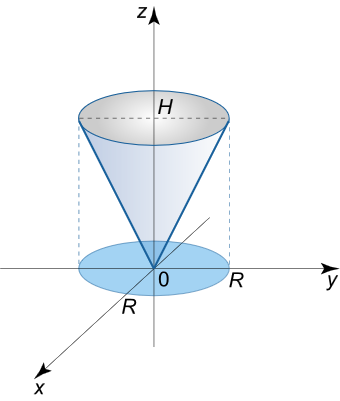
گشتاور لختی یک مخروط همگن دایرهای قائم را حول محور تقارن آن بیابید. شعاع قاعده، ارتفاع و جرم کل مخروط به ترتیب، R R R H H H m m m
شکل ۳ حل: گشتاور لختی یک جسم حول محور z z z
I z = ∭ U γ ( x , y , z ) ⋅ ( x 2 + y 2 ) d x d y d z . \large {{I_z} }={ \iiint\limits_U {\gamma \left( {x,y,z} \right)\cdot}}\kern0pt{{\left( {{x^2} + {y^2}} \right)dxdydz} .} I z = U ∭ γ ( x , y , z ) ⋅ ( x 2 + y 2 ) d x d y d z .
از آنجایی که مخروط همگن است، میتوان چگالی را به صورت γ ( x , y , z ) = γ 0 \gamma \left( {x,y,z} \right) = {\gamma _0} γ ( x , y , z ) = γ 0
I z = γ 0 ∫ U ( x 2 + y 2 ) d x d y d z . \large {{I_z} }={ {\gamma _0}\int\limits_U {\left( {{x^2} + {y^2}} \right)dxdydz} .} I z = γ 0 U ∫ ( x 2 + y 2 ) d x d y d z .
با استفاده از تبدیل مختصات استوانهای داریم:
x = r cos φ , y = r sin φ , ⇒ x 2 + y 2 = r 2 , d x d y d z = r d r d φ d z . \large {x = r\cos \varphi ,\;\;\;}\kern-0.3pt {y = r\sin \varphi ,\;\;\;} \\ \large \Rightarrow {{x^2} + {y^2} = {r^2},\;\;\;}\kern-0.3pt {dxdydz = rdrd\varphi dz.} x = r cos φ , y = r sin φ , ⇒ x 2 + y 2 = r 2 , d x d y d z = r d r d φ d z .
محدوده متغیرهای جدید به صورت زیر خواهد بود:
0 ≤ r ≤ R , 0 ≤ φ ≤ 2 π , r H R ≤ z ≤ H . \large {0 \le r \le R,\;\;\;}\kern0pt {0 \le \varphi \le 2\pi ,\;\;\;}\kern0pt {r\frac{H}{R} \le z \le H.} 0 ≤ r ≤ R , 0 ≤ φ ≤ 2 π , r R H ≤ z ≤ H .
بنابراین، گشتاور لختی برابر است با:
I z = γ 0 ∫ 0 2 π d φ ∫ 0 R r 3 d r ∫ r H R H d z = γ 0 ∫ 0 2 π d φ ∫ 0 R r 3 d r ⋅ [ z ∣ r H R H ] = γ 0 ∫ 0 2 π d φ ∫ 0 R r 3 ( H – r H R ) d r = γ 0 H ∫ 0 2 π d φ ∫ 0 R ( r 3 – r 4 R ) d r = γ 0 H ∫ 0 2 π d φ ⋅ [ ( r 4 4 – r 5 5 R ) ∣ 0 R ] = γ 0 H ∫ 0 2 π ( R 4 4 – R 4 5 ) d φ = γ 0 H R 4 20 ∫ 0 2 π d φ = γ 0 H R 4 20 ⋅ 2 π = γ 0 π H R 4 10 . \large { { I _z } = {\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_{r\frac{H}{R}}^H {dz} } = {{\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot \left[ {\left. z \right|_{r\frac{H}{R}}^H} \right] } \\ \large = {{\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}\left( {H – r\frac{H}{R}} \right)dr} } = {{\gamma _0}H\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {\left( {{r^3} – \frac{{{r^4}}}{R}} \right)dr} }\\ \large = {{\gamma _0}H\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4} – \frac{{{r^5}}}{{5R}}} \right)} \right|_0^R} \right] } = {{\gamma _0}H\int\limits_0^{2\pi } {\left( {\frac{{{R^4}}}{4} – \frac{{{R^4}}}{5}} \right)d\varphi } } \\ \large = {\frac{{{\gamma _0}H{R^4}}}{{20}}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{{\gamma _0}H{R^4}}}{{20}} \cdot 2\pi } = {\frac{{{\gamma _0}\pi H{R^4}}}{{10}}.} I z = γ 0 0 ∫ 2 π d φ 0 ∫ R r 3 d r r R H ∫ H d z = γ 0 0 ∫ 2 π d φ 0 ∫ R r 3 d r ⋅ [ z ∣ r R H H ] = γ 0 0 ∫ 2 π d φ 0 ∫ R r 3 ( H – r R H ) d r = γ 0 H 0 ∫ 2 π d φ 0 ∫ R ( r 3 – R r 4 ) d r = γ 0 H 0 ∫ 2 π d φ ⋅ ( 4 r 4 – 5 R r 5 ) 0 R = γ 0 H 0 ∫ 2 π ( 4 R 4 – 5 R 4 ) d φ = 20 γ 0 H R 4 0 ∫ 2 π d φ = 20 γ 0 H R 4 ⋅ 2 π = 10 γ 0 π H R 4 .
چگالی γ 0 {\gamma _0} γ 0 m m m
m = γ 0 V , V = 1 3 π R 2 H \large {m = {\gamma _0}V,\;\;\;}\kern-0.3pt {V = \frac{1}{3}\pi {R^2}H} m = γ 0 V , V = 3 1 π R 2 H
بنابراین:
γ 0 = m V = m 1 3 π R 2 H = 3 m π R 2 H . \large {{\gamma _0} = \frac{m}{V} } = {\frac{m}{{\frac{1}{3}\pi {R^2}H}} } = {\frac{{3m}}{{\pi {R^2}H}}.} γ 0 = V m = 3 1 π R 2 H m = π R 2 H 3 m .
نهایتاً خواهیم داشت:
$$ \large \require{cancel}<br />
{{I_z} = \frac{{{\gamma _0}\pi H{R^4}}}{{10}} }<br />
= {\frac{{3m}}{{\bcancel{\pi} {R^2}\bcancel{H}}} \cdot \frac{{\bcancel{\pi} \bcancel{H}{R^4}}}{{10}} }<br />
= {\frac{{3m{R^2}}}{{10}}.} $$
نکته جالب توجه در اینجا، مستقل بودن گشتاور لختی مخروط از ارتفاع آن است.
مثال ۵
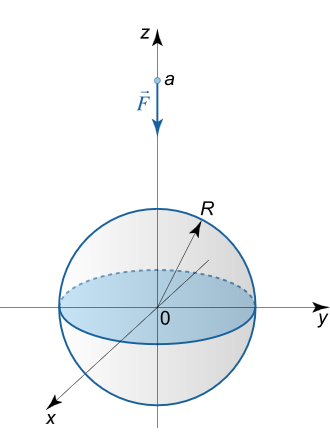
به ازای چه نیرویی یک کره توپر همگن به جرم M M M m m m a a a a > R {a \gt R} a > R
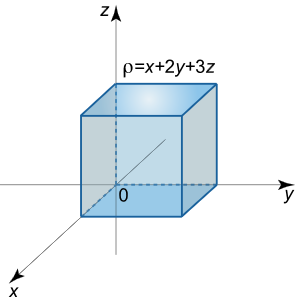
حل: بدون از دست دادن کلیت مسئله، نقطه را روی محور z z z ( 0 , 0 , a ) \left( {0,0,a} \right) ( 0 , 0 , a )
شکل ۴ ابتدا پتانسیل کره و سپس نیروی جاذبه بین نقطه و کره را محاسبه میکنیم. برای به دست آوردن پتانسیل کره، به جای محاسبه انتگرال سه گانه بهتر است ابتدا از انتگرال سطحی استفاده کنیم و سپس از جواب به دست آمده انتگرال بگیریم.
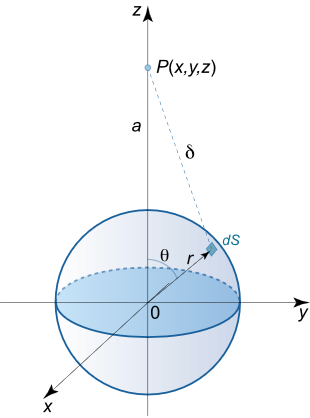
شکل ۵ کرهای به شعاع دلخواه r r r r ≤ R r \le R r ≤ R
d M = ρ ( r ) d r d S \large dM = \rho \left( r \right)drdS d M = ρ ( r ) d r d S
که در آن، ρ ( r ) \rho \left( r \right) ρ ( r ) d r dr d r P P P
d u = ρ ( r ) d r ∬ S d S δ = ρ ( r ) d r ⋅ ∬ S d S a 2 + r 2 – 2 a r cos θ , \large {du = \rho \left( r \right)dr\iint\limits_S {\frac{{dS}}{\delta }} } = {\rho \left( r \right)dr \cdot}\kern0pt{ \iint\limits_S {\frac{{dS}}{{\sqrt {{a^2} + {r^2} – 2ar\cos \theta } }}} ,} d u = ρ ( r ) d r S ∬ δ d S = ρ ( r ) d r ⋅ S ∬ a 2 + r 2 –2 a r cos θ d S ,
که در آن، δ \delta δ d S dS d S P P P a a a r r r θ \theta θ
المان سطحی به صورت d S = r 2 sin θ d θ d φ dS= {r^2}\sin \theta d\theta d\varphi d S = r 2 sin θ d θ d φ
d u = ρ ( r ) d r ⋅ ∫ S d S a 2 + r 2 – 2 a r cos θ = ρ ( r ) d r ∫ 0 2 π d φ ⋅ ∫ 0 π r 2 sin θ d θ a 2 + r 2 – 2 a r cos θ = ρ ( r ) d r ⋅ 2 π r 2 ⋅ ∫ 0 π sin θ d θ a 2 + r 2 – 2 a r cos θ . \large {{du }={ \rho \left( r \right)dr \cdot}}\kern0pt{{\int\limits_S {\frac{{dS}}{{\sqrt {{a^2} + { r ^ 2 } – 2 ar\cos \theta } }}} }} \\ \large = {{\rho \left( r \right)dr\int\limits _ 0 ^ { 2\pi } {d\varphi } \cdot}\kern0pt{ \int\limits_0^\pi {\frac{{{ r ^ 2 }\sin \theta d\theta } } { { \sqrt {{ a ^ 2} + { r ^ 2 } – 2 a r\cos \theta } }}} }} \\ \large = {{\rho \left( r \right)dr \cdot 2\pi {r^2} \cdot}\kern0pt{ \int\limits_0^\pi {\frac{{\sin \theta d\theta }}{{\sqrt {{a^2} + {r^2} – 2ar\cos \theta } }}} .}} d u = ρ ( r ) d r ⋅ S ∫ a 2 + r 2 –2 a r cos θ d S = ρ ( r ) d r 0 ∫ 2 π d φ ⋅ 0 ∫ π a 2 + r 2 –2 a r cos θ r 2 sin θ d θ = ρ ( r ) d r ⋅ 2 π r 2 ⋅ 0 ∫ π a 2 + r 2 –2 a r cos θ sin θ d θ .
این انتگرال را به طور جداگانه با استفاده از تغییر متغیر زیر حل میکنیم:
v = a 2 + r 2 − 2 a r cos θ . \large {v = {a^2} + {r^2} }-{ 2ar\cos \theta .} v = a 2 + r 2 − 2 a r cos θ .
بنابراین، میتوان نوشت:
d v = 2 a r sin θ d θ , ⇒ sin θ d θ = d v 2 a r . \large {dv = 2ar\sin \theta d\theta ,\;\;}\Rightarrow {\sin \theta d\theta = \frac{{dv}}{{2ar}}.} d v = 2 a r sin θ d θ , ⇒ sin θ d θ = 2 a r d v .
در نتیجه، جواب انتگرال به صورت زیر خواهد بود:
I = ∫ sin θ d θ a 2 + r 2 – 2 a r cos θ = ∫ d v 2 a r v \large {I }={ \int {\frac{{\sin \theta d\theta }}{{\sqrt {{a^2} + {r^2} – 2ar\cos \theta } }}} } = {\int {\frac{{dv}}{{2ar\sqrt v }}}} I = ∫ a 2 + r 2 –2 a r cos θ sin θ d θ = ∫ 2 a r v d v
= 1 a r ∫ d v 2 v = v a r = 1 a r a 2 + r 2 – 2 a r cos θ . \large = \frac{1}{{ar}}\int {\frac{{dv}}{{2\sqrt v }}} = {\frac{{\sqrt v }}{{ar}} } = {\frac{1}{{ar}}\sqrt {{a^2} + {r^2} – 2ar\cos \theta } .} = a r 1 ∫ 2 v d v = a r v = a r 1 a 2 + r 2 –2 a r cos θ .
با جایگذاری مقدار انتگرال، خواهیم داشت:
d u = ρ ( r ) d r ⋅ 2 π r 2 ⋅ 1 a r ⋅ [ ( a 2 + r 2 – 2 a r cos θ ) ∣ θ = 0 θ = π ] = 2 π r ρ ( r ) d r a ⋅ [ a 2 + r 2 + 2 a r − a 2 + r 2 – 2 a r ] = 2 π r ρ ( r ) d r a ⋅ [ ( a + r ) 2 – ( a – r ) 2 ] = 2 π r ρ ( r ) d r a ⋅ 2 r = 4 π r 2 ρ ( r ) d r a . \large { d u } = { \rho \left( r \right)dr \cdot 2\pi {r^2} \cdot \frac{1}{{ar}} \cdot}\kern0pt{ \left[ {\left. {\left( {\sqrt {{a^2} + {r^2} – 2ar\cos \theta } } \right)} \right|_{\theta = 0}^{\theta = \pi }} \right] } \\ \large = {{\frac{{2\pi r\rho \left( r \right)dr}}{a} \cdot}\kern0pt{ \left[ {\sqrt {{ a ^2 } + {r ^ 2 } + 2ar} }\right.}-{\left.{ \sqrt {{a^2} + {r^2} – 2ar} } \right] }} \\ \large = {{\frac{{2\pi r\rho \left( r \right)dr}}{a} \cdot}\kern0pt{ \left[ {\sqrt {{{\left( {a + r} \right)}^2}} – \sqrt {{{\left( {a – r} \right)}^2}} } \right] }} \\ \large = {\frac{{2\pi r\rho \left( r \right)dr}}{a} \cdot 2r } = {\frac{{4\pi {r^2}\rho \left( r \right)dr}}{a}.} d u = ρ ( r ) d r ⋅ 2 π r 2 ⋅ a r 1 ⋅ [ ( a 2 + r 2 –2 a r cos θ ) θ = 0 θ = π ] = a 2 π r ρ ( r ) d r ⋅ [ a 2 + r 2 + 2 a r − a 2 + r 2 –2 a r ] = a 2 π r ρ ( r ) d r ⋅ [ ( a + r ) 2 – ( a – r ) 2 ] = a 2 π r ρ ( r ) d r ⋅ 2 r = a 4 π r 2 ρ ( r ) d r .
اکنون میتوانیم پتانسیل کره را محاسبه کنیم. برای سادگی فرض میکنیم چگالی کره ثابت و برابر با ρ 0 {\rho_0} ρ 0
u = ∫ 0 R d u = ∫ 0 R 4 π r 2 ρ 0 d r a = 4 π ρ 0 a ∫ 0 R r 2 d r = 4 π ρ 0 a [ ( r 3 3 ) ∣ 0 R ] = 4 π ρ 0 R 3 3 a . \large {u = \int\limits_0^R {du} } = {\int\limits_0^R {\frac{{4\pi {r^2}{\rho _0}dr}}{a}} } = {\frac{{4\pi {\rho _0}}}{a}\int\limits_0^R {{r^2}dr} } \\ \large = {\frac{{4\pi {\rho _0}}}{a}\left[ {\left. {\left( {\frac{{{r^3}}}{3}} \right)} \right|_0^R} \right] } = {\frac{{4\pi {\rho _0}{R^3}}}{{3a}}.} u = 0 ∫ R d u = 0 ∫ R a 4 π r 2 ρ 0 d r = a 4 π ρ 0 0 ∫ R r 2 d r = a 4 π ρ 0 ( 3 r 3 ) 0 R = 3 a 4 π ρ 0 R 3 .
در جواب به دست آمده، 4 3 π R 3 = V {\large\frac{4}{3}\normalsize} \pi {R^3} = V 3 4 π R 3 = V ρ 0 V = M {\rho_0}V = M ρ 0 V = M a a a a > R a>R a > R
u = M a . \large u = \frac{M}{a}. u = a M .
با استفاده از پتانسیل به دست آمده، به راحتی میتوان نیرو را به دست آورد. از آنجایی که رابطه زیر را داریم:
F = – G m grad u , \large \mathbf{F} = – Gm\,\mathbf{\text{grad}}\,u, F = – G m grad u ,
نیروی جاذبه بین کره و نقطه برابر است با:
F = G m ∂ u ∂ z = G m [ ∂ ∂ z ( M z ) ] ∣ z = a = – G m M a 2 . \large {F = Gm\frac{{\partial u}}{{\partial z}} } = {Gm{\left. {\left[ {\frac{\partial }{{\partial z}}\left( {\frac{M}{z}} \right)} \right]} \right|_{z = a}} } = { – G\frac{{mM}}{{{a^2}}}.} F = G m ∂ z ∂ u = G m [ ∂ z ∂ ( z M ) ] z = a = – G a 2 m M .
علامت منفی در فرمول بالا، بدین معنی است که این نیرو در خلاف جهت محور z z z
همانگونه که مشاهده میکنیم، نیروی جاذبه بین کره و نقطه مانند نیروی جاذبه بین دو جرم نقطهای است. این یکی از نتایج اصلی در اخترفیزیک و مکانیک نجومی است. به همین دلیل، هنگام توصیف حرکت سیارهها و ستارهها، میتوان آنها را مانند نقاط در نظر گرفت. نیوتن برای اثبات این نتیجه حتی مجبور شد انتشار مقاله شاهکار خود درباره علم نجوم را به تأخیر اندازد. شاید این سختیها به دلیل استفاده نکردن از مختصات کروی برای حل این مسئله بوده است.
مثال ۶
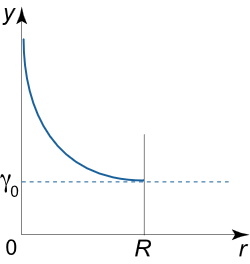
فرض کنید که چگالی سیارهای به شعاع R R R γ ( r ) = R + r 2 r γ 0 \gamma \left( r \right) = \frac{{R + r}}{{2r}}{\gamma _0} γ ( r ) = 2 r R + r γ 0
حل: چگالی سیاره به ازای شعاعهای مختلف، تغییر میکند. اگر r = R r=R r = R
γ ( R ) = R + R 2 R γ 0 = γ 0 , \large {\gamma \left( R \right) = \frac{{R + R}}{{2R}}{\gamma _0} }={ {\gamma _0},} γ ( R ) = 2 R R + R γ 0 = γ 0 ,
که در آن، γ 0 {\gamma_0} γ 0 r → 0 r \to 0 r → 0 γ → ∞ \gamma \to \infty γ → ∞
شکل ۶ جرم سیاره را با استفاده از انتگرال سه گانه محاسبه میکنیم:
M = ∭ U d V . \large M = \iiint\limits_U {dV} . M = U ∭ d V .
با استفاده از تبدیل مختصات کروی داریم:
M = ∭ U d V = ∭ U γ ( r ) r 2 sin θ d r d φ d θ = ∭ U R + r 2 r γ 0 r 2 sin θ d r d φ d θ = γ 0 2 ∫ U ( R + r ) r sin θ d r d φ d θ = γ 0 2 ∫ 0 R ( R + r ) r d r ∫ 0 2 π d φ ⋅ ∫ 0 π sin θ d θ = γ 0 2 ∫ 0 R ( R + r ) r d r ∫ 0 2 π d φ ⋅ [ ( – cos θ ) ∣ 0 π ] = γ 0 2 ∫ 0 R ( R + r ) r d r ∫ 0 2 π d φ ⋅ ( – cos π + cos 0 ) = γ 0 ∫ 0 R ( R + r ) r d r ∫ 0 2 π d φ = γ 0 ∫ 0 R ( R + r ) r d r ⋅ 2 π = 2 π γ 0 ∫ 0 R ( R r + r 2 ) d r = 2 π γ 0 [ ( R r 2 2 + r 3 3 ) ∣ 0 R ] = 2 π γ 0 ( R 3 2 + R 3 3 ) = 2 π γ 0 5 R 3 6 = 5 π γ 0 R 3 3 . \large {M = \iiint\limits_U {dV} } = {\iiint\limits_U {\gamma \left( r \right){r^2}\sin \theta drd\varphi d\theta } } \\ \large = {\iiint \limits _ U {\frac{{R + r}}{{2r}}{\gamma _0}{r^2}\sin \theta drd \varphi d\theta } } = {\frac{{{\gamma _0}}}{2}\int\limits_U {\left( {R + r} \right)r\sin \theta drd\varphi d\theta } } \\ \large = {{\frac{ { { \gamma _ 0 }} } { 2 }\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits _ 0 ^ { 2 \pi } { d \varphi } \cdot}\kern0pt{ \int\limits_0^\pi {\sin \theta d\theta } }} = {{\frac{{{\gamma _ 0 } }} { 2 } \int \limits _ 0 ^ R {\left( {R + r} \right)rdr} \int\limits _ 0 ^ { 2\pi } {d\varphi } \cdot}\kern0pt{ \left[ {\left. {\left( { – \cos \theta } \right)} \right|_0^\pi } \right] }} \\ \large = {{\frac{{{\gamma _ 0 } }} { 2 }\int\limits _ 0 ^ R {\left( {R + r} \right)rdr} \int\limits _ 0 ^ { 2 \pi } {d\varphi } \cdot}\kern0pt{ \left( { – \cos \pi + \cos 0} \right) }} = {{\gamma _0}\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits _0 ^ { 2 \pi } { d \varphi } } \\ \large = {{\gamma _0}\int\limits _ 0 ^ R {\left( {R + r} \right)rdr} \cdot 2\pi } = {2\pi {\gamma _ 0 }\int\limits _ 0 ^ R {\left( {Rr + { r ^ 2 }} \right)dr} } \\ \large = {2\pi {\gamma _ 0}\left[ {\left. {\left( {\frac { { R{ r ^ 2 } } } { 2} + \frac { { {r ^ 3 } } } {3 }} \right)} \right | _ 0 ^ R } \right] } = {2\pi {\gamma _0}\left( {\frac{{{R^3}}}{2} + \frac { { { R ^ 3 } } } {3 } } \right) } \\ \large = {2\pi {\gamma _ 0 } \frac { { 5 { R ^ 3} } }{ 6 } } = { \frac { { 5 \pi {\gamma _ 0 } { R ^ 3 } } } { 3} . } M = U ∭ d V = U ∭ γ ( r ) r 2 sin θ d r d φ d θ = U ∭ 2 r R + r γ 0 r 2 sin θ d r d φ d θ = 2 γ 0 U ∫ ( R + r ) r sin θ d r d φ d θ = 2 γ 0 0 ∫ R ( R + r ) r d r 0 ∫ 2 π d φ ⋅ 0 ∫ π sin θ d θ = 2 γ 0 0 ∫ R ( R + r ) r d r 0 ∫ 2 π d φ ⋅ [ ( – cos θ ) ∣ 0 π ] = 2 γ 0 0 ∫ R ( R + r ) r d r 0 ∫ 2 π d φ ⋅ ( – cos π + cos 0 ) = γ 0 0 ∫ R ( R + r ) r d r 0 ∫ 2 π d φ = γ 0 0 ∫ R ( R + r ) r d r ⋅ 2 π = 2 π γ 0 0 ∫ R ( R r + r 2 ) d r = 2 π γ 0 ( 2 R r 2 + 3 r 3 ) 0 R = 2 π γ 0 ( 2 R 3 + 3 R 3 ) = 2 π γ 0 6 5 R 3 = 3 5 π γ 0 R 3 .
از آنجایی که حجم سیاره 4 3 π R 3 {\large\frac{4}{3}\normalsize} \pi {R^3} 3 4 π R 3
M = 5 π γ 0 R 3 3 = 5 4 γ 0 V . \large {M = \frac{{5\pi {\gamma _0}{R^3}}}{3} }={ \frac{5}{4}{\gamma _0}V.} M = 3 5 π γ 0 R 3 = 4 5 γ 0 V .
همانطورکه میبینیم، جرم سیاره در مقایسه با حالتی که چگالی به طور یکنواخت توزیع میشود، 25 25 25
اگر مطلب بالای برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^