الگوریتم بازی مار و پله همراه با کد – به زبان ساده
بازی مار و پله (Snakes and Ladders)، یک بازی باستانی هندی است که اکنون یک بازی کلاسیک جهانی محبوب محسوب میشود. این بازی قابل انجام بین دو یا تعداد بیشتری بازیکن است. صفحه بازی مار و پله، شطرنجی است؛ در این بازی، در برخی از خانهها نردبانهایی وجود دارد که فرد را به خانههای بالاتر میرساند و در بعضی از خانهها، مارهایی وجود دارد که فرد را اصطلاحا نیش میزنند و به خانههای پایینتری انتقال میدهند (جایی که دم مار در آن قرار دارد). بازی به این صورت انجام میشود که هر بازیکن تاس میاندازد و با توجه به عددی که میآید، تعداد خانههایی را به جلو حرکت میکند. بسته به عدد تاس، ممکن است فرد در یک خانه عادی، دارای نربان و یا دارای مار قرار بگیرد. در «مساله مار و پله» (Snake and Ladder Problem)، هدف پیدا کردن کمترین تعداد دفعات پرتاب تاس لازم برای رسیدن به مقصد (آخرین خانه در صفحه شطرنجی) از مبدا (اولین خانه) است. این مساله کمی با بازی تختهای متداول مار و پله که افراد بازی میکنند متفاوت است و در آن، بازیکن بر عددی که در پرتاب تاس به دست میآید کنترل دارد و باید اعدادی را پیدا کند که با کمترین تعداد پرتاب تاس به خانه نهایی برسد. در ادامه، الگوریتم بازی مار و پله (در واقع الگوریتم لازم برای حل این مساله) ارائه و پیادهسازی آن در زبانهای برنامهنویسی «پایتون» (Python)، «جاوا» (Java)، «سیپلاسپلاس» (++C) و «سیشارپ» (#C) انجام شده است.


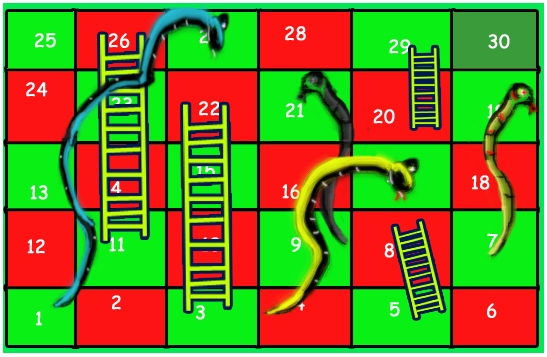
الگوریتم بازی مار و پله
برای مثال، در صفحه بازی موجود در تصویر بالا، تعداد پرتابهای تاس لازم برای رسیدن از خانه ۱ به خانه ۳۰ برابر با سه است. گامهای زیر برای آنکه بازیکن با سه پرتاب تاس به نتیجه برسد انجام میشود.
- ابتدا تاس دو انداخته میشود تا بازیکن از خانه یک به خانه سه برود و با استفاده از نردبان به خانه ۲۲ برسد.
- سپس، تاس ۶ انداخته میشود تا فرد از خانه ۲۲ به خانه ۲۸ برسد.
- در نهایت، با انداختن تاس ۲، بازیکن به خانه ۳۰ (مقصد نهایی) میرسد.
برخی از دیگر راهکارهای موجود برای حل مساله مار و پله (با کمترین تعداد پرتاب تاس) عبارتند از: (2, 2, 6)، (2, 4, 4) و (2, 3, 5).
ایده موجود برای حل این مساله در حالت کلی آن است که صفحه بازی به صورت یک گراف جهتدار در نظر گرفته شود. اکنون، مساله یافتن کوتاهترین مسیر در گراف است. هر «راس» (Vertex) از گراف، دارای «یالی» (Edge) به شش راس بعدی است؛ اگر راسهای بعدی دارای نردبان یا مار نباشند. اگر هر یک از شش راس دارای مار یا نردبان باشند، یال از راس کنونی به راس بالای نردبان یا دم مار متصل میشود.
با توجه به اینکه همه یالها دارای وزنهای برابری هستند، میتوان کوتاهترین مسیر را با استفاده از «جستجوی اول عمق» (Breadth First Search) کشف کرد. در ادامه، پیادهسازی ایده بالا با استفاده از زبانهای برنامهنویسی گوناگون انجام شده است. ورودی با دو چیز نمایش داده شده است: N که تعداد خانههای صفحه بازی است و آرایه [move[0…N-1 با اندازه N. یک ورودی [move[i برابر با ۱- است اگر هیچ مار یا نردبانی از i وجود نداشته باشد؛ در غیر این صورت، [move[i حاوی اندیس سلول مقصد برای مار یا نردبان در i است.
پیاده سازی الگوریتم بازی مار و پله در ++C
پیاده سازی الگوریتم بازی مار و پله در پایتون
پیادهسازی بازیها با پایتون به غیر از نوعی تمرین کدنویسی و طراحی الگوریتم بسیار خوب و جنبه سرگرمی که دارد، باعث آشنایی با تکنولوژیهای مختلف نیز میشود. یکی دیگر از بهترین تمرینها در این زمینه پیادهسازی بازی منچ است. برای آموزش و مشاهده یکی از تکنیکهای خوب برای پیادهسازی منچ در پایتون مطلب آموزش ساخت بازی منچ با پایتون، به زبان ساده و همراه با کد را از مجله فرادرس مطالعه کنید.
پیاده سازی الگوریتم بازی مار و پله در جاوا
خروجی:
Min Dice throws required is 3
پیچیدگی زمانی راهکار بالا از درجه (O(N است؛ زیرا هر سلول تنها یکبار به «صف» (Queue) اضافه و کم میشود و یک فرایند معمول افزودن به صف یا حذف کردن از آن از درجه زمانی (O(1 است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- زبان برنامهنویسی پایتون (Python) — از صفر تا صد
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
^^













جاوااسکریپت نیست ؟
سلام وقت بخیر و خسته نباشید به شما استاد گرامی
اگه امکانش باشه با بیسیک فور اندروید هم کدش رو قرار بدین
با تشکر