گیت برگشت پذیر توفولی (CCNOT) – به زبان ساده
در مبحث محاسبات و مدارات منطقی، گیت ۳ ورودی و ۳ خروجی توفولی (Toffoli) گیتی جامع و برگشتپذیر است. جامع بودن به این معنی است که هر گیت یا مدارهای برگشتپذیر دیگر را میتوان توسط این گیت طراحی و پیادهسازی کرد. برگشتپذیری نیز به طور ساده و خلاصه بیان میکند که با داشتن خروجی یک گیت میتوانیم به مقادیر ورودی آن پی ببریم. در ادامه این مقاله با ما همراه باشید تا بیشتر با گیت توفولی آشنا شویم.


برگشت پذیری
از نقطه نظر ریاضی، یک تابع منطقی زمانی برگشتپذیر است که به ازای هر خروجی یک ورودی منحصر به فرد وجود داشته باشد؛ یعنی رابطه همواره برقرار باشد. در این صورت با برگشت پذیر بودن ، تابع به فرم وجود دارد تا مقادیر را به نگاشت کند.
گیتهای برگشتپذیر از سال 1960 تا کنون به دلیل حرارت بسیار کمی که تولید میکنند، مورد مطالعه قرار گرفتهاند. در یک گیت عادی تعداد خروجیها در واقع اطلاعات خروجی از تعداد ورودیها (اطلاعات ورودی) کمتر است. میتوان گفت در گیتهای عادی، اطلاعات ورودی از بین میروند که از بین رفتن اطلاعات به معنی هدر رفتن انرژی در قالب گرما است.
همچنین به دلیل این که تعداد ورودی و خروجیهای گیت برابر است، با نگاه به خروجیها میتوانیم به مقادیر ورودی دست پیدا کنیم. بحث برگشتپذیری برای معماران و مهندسان کامپیوتر از اهمیت خیلی زیادی برخوردار است.
عملکرد گیت توفولی (CCNOT)
نام دیگر گیت توفولی، Controlled Controlled NOT یا به اختصار CCNOT است. در واقع این اسم از چگونگی عملکرد آن حکایت دارد. از کلمه Controlled میتوانیم پی ببریم که ساختار گیت مذکور، کنترلی بوده و عمل کردن آن شرطی است. گیتهای کنترلی به ما اجازه پیادهسازی ساختاری شرطی شبیه به if else را میدهند. میدانیم واحد اصلی پردازش اطلاعات کلاسیکی، یعنی «بیت» (bit) دو مقدار ۰ و ۱ را دارد. پس درستی شرط را با ۱ و غلط بودن را با ۰ نمایش میدهیم. به طور مثال گیت دو ورودی Controlled NOT، تنها در صورتی عمل میکند که بیت کنترلی (یا کیوبیت در منطق محاسبات کوانتومی) مقدار منطقی ۱ را داشته باشد. در این صورت بیت دوم (موسوم به بیت هدف) به صورت معکوس، یعنی NOT شده ظاهر میشود. به بیانی دیگر در این گیت، بیت کنترلی بدون تغییر و XOR دو بیت کنترلی و هدف در خروجی ظاهر میشود. شماتیک مداری و جدول درستی این گیت در شکل (۱) آمده است.
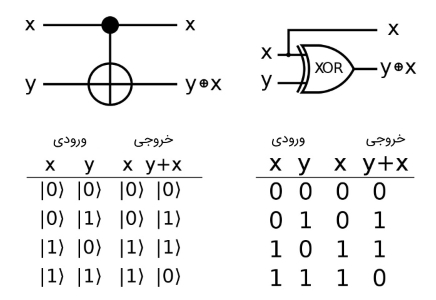
جدول درستی گیت (Exclusive OR : XOR) به صورت زیر است. خروجی این گیت تنها زمانی ۱ است که فقط یکی از دو ورودیها ۱ باشد.
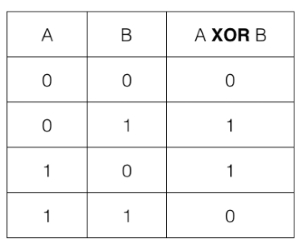
با تعمیم مطلب فوق، در مورد عملکرد گیت CCNOT میتوانیم بگوییم که این گیت فقط و فقط وقتی عمل میکند که هر دو بیت (کیوبیت) کنترلی آن مقدار منطقی ۱ را داشته باشند. در این صورت بیت هدف در خروجی به شکل NOT شده ظاهر میشود. شماتیک مداری این گیت ۳ ورودی به شکل زیر است:
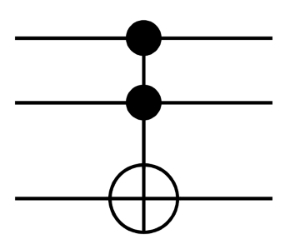
در واقع میتوان گفت که این گیت، AND بیتهای کنترلی را محاسبه و نتیجه را با بیت هدف XOR میکند. جدول درستی این گیت در جدول زیر آمده است:
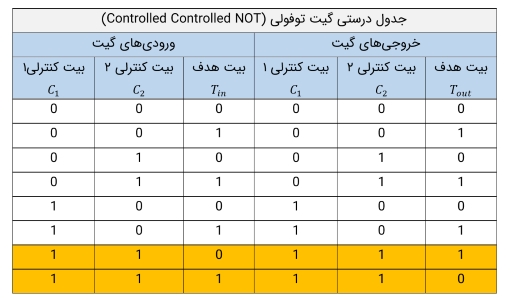
جامعیت گیت توفولی
برای برگشتپذیر بودن یک گیت، باید تعداد خروجی ها با ورودیها برابر باشد. برای گیتهای تک ورودی فقط دو گیت NOT و شناسایی (گیت شناسایی تغییری در بیت ایجاد نمیکند) گیتهایی برگشتپذیر هستند. برای گیتهای دو ورودی نیز فقط گیت CNOT است که بیت اول را بدون تغییر و XOR بیت اول و دوم به خروجی میدهد (شکل 1).
گیتهای برگشتپذیر زیادی وجود دارند که نمیتوان آنها را توسط گیتهای NOT و XOR پیادهسازی کرد. در واقع گیتها یا مدارات ساخته شده با این دو گیت جامع نیستند. پس اگر بخواهیم تابع دلخواهی را توسط گیتهای برگشتپذیر محاسبه و پیاده سازی گنیم، به گیت دیگری نیاز داریم. گیت توفولی که توسط توماس توفولی (Tommaso Toffoli) که در سال 1980 ارائه شد، میتواند برای این امر گزینه مناسبی باشد.
توسط مجموعهای از گیتهای توفولی میتوانیم هر محاسبه (تابع حقیقی) را به طور برگشتپذیری عملیاتی کنیم. در واقع برای هر «تابع منطقی» (Boolean Function) به فرم میتوانیم مداری متشکل از چند گیت توفولی بسازیم که مقادیر و تعدادی صفر و یک اضافی را از ورودی بگیرد و در خروجی عملیات متناظر با تابع را به همراه بیتهای اضافی نتیجه دهد.
میدانیم که در محاسبات کوانتومی تمامی گیتها نگاشتی یک به یک را انجام داده و در نتیجه برگشتپذیرند. عملگر یا اپراتور گیت توفولی نیز به صورت کوانتومی در ژانویه سال 2009 در دانشگاه اینسبراک استرالیا ارائه شد. نمایش ماتریسی عملگر توفولی یک ماتریس ۸ در ۸ به فرم زیر است.

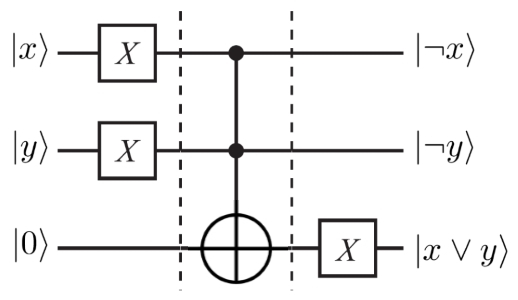
گیت کوانتومی توفولی به همراه گیتهای تک کیوبیتی دیگر میتواند محاسبات جامع و فراگیر را انجام و تمامی گیتها و محاسبات کلاسیکی را پیادهسازی کند. به عنوان مثال، در شکل (3) با قرار دادن گیت NOT بر سر راه کیوبیتهای کنترلی قبل از ورود به گیت توفولی و NOT کردن نتیجه نهایی گیت توفولی میتوانیم یک گیت OR بسازیم. در شکل زیر بلوک X، همان ماتریس پائولی x به فرم است که در محاسبات کوانتومی گیت NOT محسوب میشود.
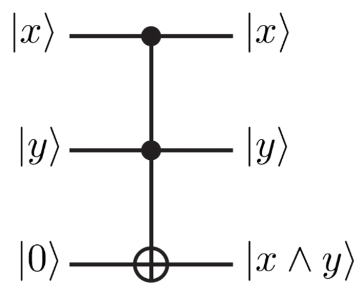
به عنوان مثالی دیگر، طبق شکل (4) اگر همیشه کیوبیت ورودی هدف به گیت توفولی را صفر قرار دهیم، میتوانیم گیت AND بسازیم. همچنین میتوان با قرار دادن یک گیت NOT بر سر راه خروجی گیت شکل (4)، یک گیت NAND که خود گیتی فراگیر و جامع است را نیز ساخت.
در صورت علاقهمندی به مباحث مرتبط در زمینه علوم و مهندسی کامپیوتر، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- کیوبیت — به زبان ساده
- کامپیوتر کوانتومی -- به زبان ساده
- سیستمهای باینری به زبان ساده – بخش اول: اعداد باینری
- منطق دیجیتال — از صفر تا صد
^^













سلام متلب بسیار عالی و قابل فهم بود.
در شکل 3 اشتباهی وجود دارد.در قسمت وسط باید گیت تفولی را داشته باشیم در صورتی که کیوبیت صفر به یک بلوک X داده شده. سپاس
سلام.
شکل اصلاح شد.
از همراهی و بازخورد شما سپاسگزاریم.