گراف اویلری — به زبان ساده

در آموزشهای قبلی مجله فرادرس، درباره گراف و تعاریف مربوط به آن صحبت کردیم. در این آموزش قصد داریم مفهوم گراف اویلری و شبه اویلری را بیان کنیم.
تاریخچه گراف اویلری
یک مسئله که احتمالا خیلیها با آن درگیر شدهاند، رسم یک شکل بدون برداشتن خودکار از روی کاغذ و بدون عبور مجدد از هر خط است.
در سال ۱۷۳۶ «اویلر» (Euler)، اولین بار مسئله مشهور «پلهای کونیگسبرگ» (Seven Bridges of Konigsberg) را حل کرد. مسئله به این صورت بیان میشود که آیا میتوان از نقطهای شروع به قدم زدن کرد و همه پلها را پیمود؟
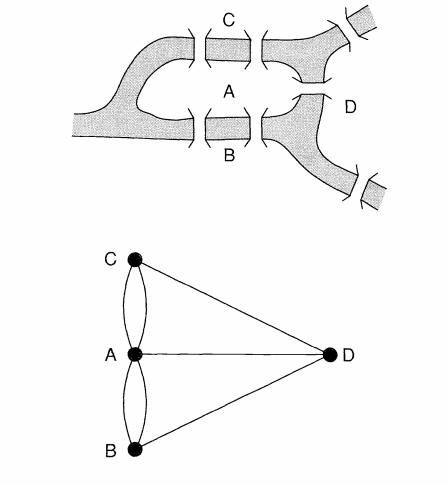
مسئله پلهای شهر کونیگسبرگ معادل این است که آیا در گراف شکل زیر، مدار یا دور اویلری وجود دارد یا خیر؟ اما مدار اویلری چیست؟ در بخش بعد به این پرسش پاسخ خواهیم داد.
تعریف گذر و مدار اویلری
در گرافهای محدود، «گذر اویلری» (Eulerian Trail) یا «مسیر اویلری» (Eulerian Path) به مسیری گفته میشود که از همه یالهای گراف فقط یک بار عبور کند. توجه به این نکته ضروری است که گذر اویلری، از هر یال فقط و فقط یک بار عبور میکند، اما میتوان از هر رأس چندین بار عبور کرد. در گراف جهت دار، گذر اویلری تبدیل به گذر جهت دار اویلری میشود.
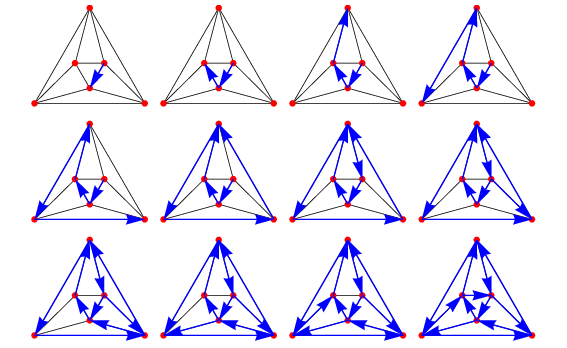
به همین ترتیب، «مدار یا دور اویلری» (Eulerian Circuit)، یک گذر اویلری است که رأس ابتدایی و انتهایی آن یکی باشد. در گراف جهت دار، دور اویلری به دور جهت دار اویلری تبدیل میشود. شکل زیر یک دور اویلری را نشان میدهد:
گراف اویلری
گراف همبند را اویلری گویند هرگاه یک مدار یا دور اویلری داشته باشد. بنابراین، گرافی اویلری است که بتوان از یک رأس شروع کرد و با فقط یک بار عبور از همه یالها، مجددا به همان رأس رسید.
اویلر ثابت کرد که شرط کافی برای وجود مدار اویلری در یک گراف، زوج بودن درجات همه رئوس است. او همچنین بدون اثبات بیان کرد که در یک گراف همبند با درجه رئوس زوج، حتما یک دور اویلری وجود دارد. در سال 1873، «کارل هایرهولزر» (Carl Hierholzer) این گزاره را اثبات کرد.
در نظریه گراف، برای گراف اویلری دو تعریف وجود دارد. یکی آنکه اگر یک گراف، مدار اویلری داشته باشد، اویلری است. تعریف دیگر آن است که اگر در یک گراف درجه همه رئوس زوج باشد، آن گراف اویلری خواهد بود.
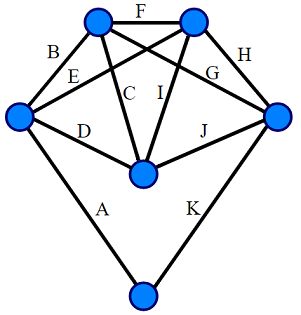
این دو تعریف برای گرافهای همبند معادل هستند. شکل زیر یک گراف اویلری همبند را نشان میدهد:
برای آنکه یک گذر اویلری وجود داشته باشد، لازم است فقط صفر یا دو رأس از گراف، درجه فرد داشته باشند. پس میتوان گفت که گراف کونیگسبرگ، اویلری نیست. اگر در یک گراف، درجه هیچ رأسی فرد نباشد، میتوان گفت که همه مسیرهای اویلری، دور هستند. اگر در یک گراف، دقیقا دو رأس از درجه فرد وجود داشته باشد، همه مسیرهای اویلری از یک رأس شروع میشوند و در رأس دیگری به جز رأس اول، پایان مییابند.
گراف غیر اویلری و شبه اویلری
اگر با شروع از یک رأس گراف، نتوان فقط یک بار از همه یالها عبور کرد، آن را گراف «غیر اویلری» (Non Eulerian) گویند. یعنی در گراف غیر اویلری اگر از یک رأس شروع کنیم، باید حداقل از یک یال دو بار عبور کنیم تا به رأس اول برسیم.
گراف غیر اویلریِ را «شبه اویلری» (Semi-Eulerian) گویند، اگر یک گذر شامل همه یالهای در آن وجود داشته باشد. به عبارت دیگر، گرافی را شبه اویلری میگویند که بتوان از یک رأس شروع کرد و با فقط یک بار عبور از همه یالها، به یک رأس دیگر و نه همان رأس اول رسید. پس گرافی که گذر اویلری دارد اما مدار اویلری ندارد، شبه اویلری است.
در گرافهای شبه اویلری، فقط و فقط دو رأس با درجه فرد وجود دارد و بقیه رئوس درجه زوج دارند. در این نوع گرافها، مسیر اویلری از رأس با درجه فرد شروع میشود و در رأسی دیگر با درجه فرد پایان مییابد. اگر مسیر در گراف شبه اویلری، از رأس با درجه زوج شروع شود، نمیتوان طبق تعریف به یک رأس دیگر رسید. یعنی عبور دوباره از یک یال لازم خواهد شد.
سه گراف نشان داده شده در شکل زیر، به ترتیب از چپ به راست، اویلری، شبه اویلری و غیر اویلری هستند:

سوالی که مطرح میشود این است که آیا یک شرط لازم و کافی برای اویلری بودن گراف وجود دارد یا خیر. قبل از پاسخ به این پرسش، لازم است یک لم ساده اثبات شود.
لم ۱: اگر در گراف ، درجه رئوس حداقل ۲ باشد، آنگاه این گراف یک دور خواهد داشت.
اثبات: اگر ، روی یک یا چند رأس خود حلقه داشته باشد، نتیجه بدیهی است. حال فرض کنید که یک گراف ساده است. را رأسی از در نظر بگیرید. میتوان یک مسیر به صورت زیر تعریف کرد:
رأس مجاور است. بنا به قانون استقرا، برای هر ، یک رأس در مجاورت رأس وجود دارد. وجود این رأس به دلیل فرض اولیه در لم، تضمین شده است. از آنجا که میتواند تعداد محدودی رأس داشته باشد، سرانجام به یک رأس میرسیم که قبلا انتخاب شده است. اگر ، اولین رأسی باشد که دو بار از آن گذر شده است، پس قسمتی از مسیر تعریف شده، تشکیل یک دور میدهد.
قضیه ۱: گراف همبند اویلری است، اگر و فقط اگر درجه همه رأسهای زوج باشد.
برای مثال، گرافهای زیر اویلری هستند، زیرا درجه همه رئوس آن زوج است:
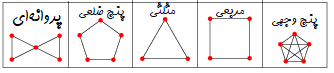
نکته: در گرافهای k - منتظم، درجه همه رئوس برابر است. اگر ، عددی فرد باشد، عددی زوج است. بنابراین طبق قضیه 1، همه گرافهای k - منتظم که در آنها k عددی فرد است، اویلری هستند.
کاربردهای گراف اویلری
در علوم بیوانفورماتیک، برای بازسازی توالی DNA از گراف اویلری استفاده میشود. همچنین در طراحی مدارهای CMOS نیز از این گراف استفاده میشود.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره سایر موضوعات مربوط به ریاضیات مطالب بیشتری یاد بگیرید، آموزشهای زیر به شما پیشنهاد میشوند:












اویلر ثابت کرد که شرط کافی برای وجود مدار اویلری در یک گراف، زوج بودن درجات همه رئوس است. یا شرط لازم؟
تعریف گراف k منتظم درست هست یعنی درجه رئوس k-1 هست ؟
زوج بودن درجه همه رئوس مشخصا شرط لازم برای وجود مدار اویلری در یک گراف هست اما کافی نیست.
به این معنی که به صرف زوج بودن همه درجه ها نمیتونیم بگیم حتما مدار اویلری موجود هست اما اگه راسی از درجه فرد داشته باشیم قطعا میتونیم بگیم که گراف فاقد دور اویلری است.
سلام. ممنون . بسیار عالی بود. موفق باشید
با تشکر، ساده و مفید