نظریه آشوب – از صفر تا صد

نظریه آشوب (Chaos Theory) شاخه‌ای از ریاضیات است که به بررسی رفتار آن دسته از سیستم‌های دینامیکی می‌پردازد که به شرایط اولیه بسیار حساس هستند. آشوب یک نظریه میان‌رشته‌ای است که بیان می‌کند: در تصادفی بودن سیستم‌های پیچیده آشوبناک (Chaotic)، الگوهای اساسی، حلقه‌های فیدبک ثابت، تکرار، خودتشابهی، فراکتال‌ها و خودسازمان‌دهی وجود دارد. طبق تعریف، واژه Chaos به معنای «حالت سردرگمی و بی‌نظمی کامل؛ فقدان کامل سازمان یا نظم» است. نظریه آشوب یک تضاد جالب است؛ علمی برای پیش‌بینی رفتار سیستم‌های «ذاتاً غیر قابل پیش‌بینی». در واقع، نظریه آشوب یک ابزار ریاضی است که به ما اجازه می‌دهد ساختارهای زیبایی را از آشوب به دست آوریم.

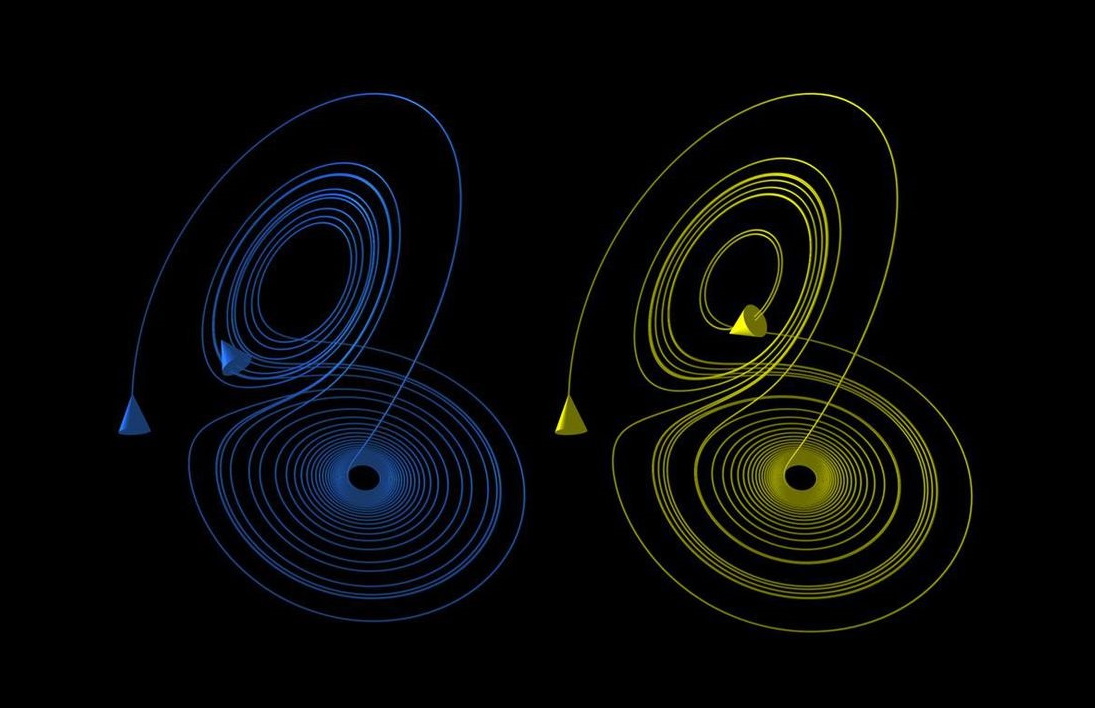
شالوده اصلی نظریه آشوب این ایده است که نظم و آشوب همیشه مخالف و در مقابل هم نیستند. سیستم‌های آشوبناک ترکیبی جذاب از نظم و آشوب هستند. از بیرون که به آن‌ها نگاه کنیم رفتاری غیرقابل پیش‌بینی دارند و بی‌نظمی از خود نشان می‌دهند، اما در درون این سیستم‌ها یک مجموعه از معادلات قطعی می‌بینیم که با نظم کار می‌کنند.

آشوب نامی است که اغلب به یک دینامیک غیرخطی اطلاق می‌شود. این عبارت برای توضیح رفتار پیچیده سیستم‌های اصطلاحاً ساده، خطی و خوش‌رفتار به کار می‌رود. رفتار آشوبی نامنظم و اغلب تصادفی به نظر می‌رسد و مشابه رفتار سیستمی است که شدیداً تحت تأثیر نویز خارجی تصادفی قرار گرفته است. تعریف ریاضی آشوب، رفتار طولانی مدت غیرقابل پیش‌بینی در یک سیستم دینامیکی قطعی به دلیل حساسیت به شرایط اولیه است (که معمولاً به نام اثر پروانه‌ای نیز شناخته می‌شود). نظریه آشوب به عنوان مطالعه کیفی رفتار نادوره‌ای ناپایدار در سیستم‌های دینامیکی غیرخطی قطعی تعریف می‌شود.

آشوب در سیستم‌های بسیار ساده رخ می‌دهد که اغلب عاری از نویز هستند. در واقع، این سیستم‌ها اساساً «قطعی» (Deterministic) هستند؛ یعنی با دانش دقیق درباره شرایط اولیه سیستم، می‌توان رفتار آینده آن را پیش‌بینی کرد. در نتیجه، شاید بتوان آشوب را به عنوان یک نوسان کران‌دار، نادوره‌ای (غیرمتناوب) و نویزی تعریف کرد. به عبارت دیگر، یک سیستم قطعی رفتار تصادفی دارد، حتی اگر هیچ ورودی تصادفی نداشته باشد. در سیستم‌های غیرخطی ناپایدار اثرات عجیب متنوعی شامل زیرهمساز (Subharmonics)، نوسان‌های شبه‌متناوب (Quasiperiodic Oscillation) و رفتار آشوبناک (Chaotic) وجود دارند.

برخی از سیستم‌هایی که قطعی هستند و رفتار آشوبی دارند، عبارتند از: سیستم‌های جوّی، منظومه شمسی، صفحات زمین‌شناسی، جریان توربولانس، رشد جمعیت، مدارهای الکترونیک قدرت و... . اما آشوب در بسیاری از زمینه‌های دیگر مانند زیست‌شناسی، علوم رایانه، اقتصاد، مهندسی، امور مالی، ریاضیات، هواشناسی، فلسفه، فیزیک، سیاست، روانشناسی، بازار سهام و رباتیک و... نیز وجود دارد.

تاریخچه نظریه آشوب

ریشه‌های نظریه آشوب به هنری پوانکاره (Henry Poincaré) بر می‌گردد که سعی کرد یک مسئله حل نشده از مکانیک سماوی لاپلاسی نیوتنی (مسئله سه جسم) را حل کند. پوانکاره پی برد که امکان دارد مدارهایی وجود داشته باشند که نادوره‌ای بوده و دائماً در حال افزایش نیستند و یا به یک نقطه ثابت همگرا نمی‌شوند. طی این تحقیقات، پوانکاره پی برد که در سیستم‌های غیرخطی ممکن است بی‌نهایت رفتار پیچیده وجود داشته باشد.

یکی از قدیمی‌ترین گزارش‌های تجربی درباره آشوب قطعی در سال ۱۹۲۷ در مجله علمی بریتانیایی ساینس (Science) چاپ شد. مهندس برق هلندی، بالتهاسار وان در پل (Balthasar van der Pol) و همکارش وان در مارک (van der Mark) یک صدای نامنظم نویزی را از گوشی تلفن متصل شده به مدار یک لوله الکترونیکی شنیدند.

نظریه آشوب تا حدودی از کار ادوارد لورنتس (Edward Lorenz) هواشناس دانشگاه ام‌آی‌تی نشئت می‌گیرد که الگوهای آب‌وهوا را در سال ۱۹۶۰ در رایانه شبیه‌سازی کرد. رایانه محدودیت حافظه داشت و لورنتس پس از مشاهده یک الگوی خاص، داده‌ها را بازگردانی و برنامه را از ابتدا اجرا می‌کرد، با این تفاوت که در این حالت، به جای آنکه مقادیر را تا ۶ رقم اعشار وارد کند، آن‌ها را تا ۳ رقم اعشار قرار می‌داد. او از اینکه نتایج در دو حالت کاملاً متفاوت بودند، شگفت‌زده شده بود. او مقاله‌ای با عنوان «پیش‌بینی پذیری: آیا بال زدن یک پروانه در برزیل گردبادی در تگزاس ایجاد می‌کند؟» (?Predictability: Does the Flap of a Butterfly's Wings in Brazil Set off a Tornado in Texas) و «اثر پروانه‌ای» (The Butterfly Effect) منتشر کرد.

در واقع، پدیده اثر پروانه‌ای که توسط لورنتس کشف شد، دستگاهی از دو معادله دیفرانسیل بود که به عنوان یک مدل ساده شده انتقال حرارت دو بعدی مورد استفاده قرار می‌گیرد. این معادلات، معادلات لورنتس نامیده می‌شوند:

$$\large \begin{align*} \frac { dx } { d t } & = \sigma ( x - y ) \\ \frac { dy } { d t} & = - x z + r x - y \\ \frac { dz } { d t } & = xy - bz \end{align*}$$

که در آن، $$\sigma$$، $$r$$ و $$b$$ پارامترهایی بدون بعد هستند. شکل زیر جاذب یا رباینده لورنتس (Lorenz Attractor) را نشان می‌دهد. چرخه کران‌دار و همگرا است، اما متناوب نیست.

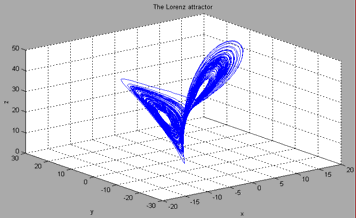
دو مؤلفه اصلی نظریه آشوب ایده‌هایی است که سیستم‌ها - هرچقدر هم که پیچیده باشند - به یک نظریه اساسی متکی هستند و آن این است که سیستم‌ها و وقایع بسیار ساده یا کوچک می‌توانند باعث رفتارها یا حوادث بسیار پیچیده شوند. این ایده اخیر به عنوان «وابستگی حساس به شرایط اولیه» شناخته می‌شود که توسط ادوارد لورنتس کشف شد. این حساسیت به شرایط اولیه «اثر پروانه‌ای» (Butterfly Effect) نامیده می‌شود و طی چند دهه گذشته تحقیقاتی با عناوین مختلف نظریه آشوب، نظریه پیچیدگی، فرایندهای تصادفی و غیره درباره آن انجام شده است.

میچل فایگنباوم (Mitchell Feigenbaum) ویژگی عمومیت یا جهان‌شمولی آشوب (نظم در بی‌نظمی) را کشف کرد و موجب شد نظریه آشوب در بسیاری از پدیده‌های مختلف به کار رود.

البته اصطلاح آشوب (Chaos) قبلاً توسط تین-یین (Tien-Yien) و جیمز یورک (James A. Yorke) در سال ۱۹۷۵ در مقاله‌ای با عنوان «Period Three Implies Chaos» معرفی شده بود. بدون شک، این مقاله در گسترش مفهوم آشوب تأثیر زیادی داشت. عامل اصلی توسعه نظریه آشوب کامپیوتر بود. بخش اعظم ریاضیات نظریه آشوب شامل تکرار فرمول‌های ریاضی ساده است که انجام دستی آن کاری نشدنی است. رایانه‌ها این محاسبات مکرر را عملی و ارقام و تصاویر امکان تجسم این سیستم‌ها را فراهم آوردند.

اهمیت نظریه آشوب

نظریه آشوب به دو دلیل دانشمندان و مهندسان را مجذوب خود کرده است:

1. نظریه آشوب ابزارهای نظری و تجربی را برای دسته‌بندی و درک رفتار پیچیده‌ای ارائه می‌کند که سایر نظریه‌ها در آن‌ها کارایی ندارند.
2. آشوب جهان‌شمول است؛ یعنی در نوسان‌سازهای مکانیکی، مدارهای الکتریکی، واکنش‌های شیمیایی، سیستم‌های اپتیکی، سلول‌های عصبی، لیزرها و... کاربرد دارد.

رفتار آشوبی ویژگی‌های جهانی کمی و کیفی باورنکردنی را نشان می‌دهد. این ویژگی‌های جهانی مستقل از جزئیات سیستم هستند. جهانی بودن بدین معنی است که آنچه را از مطالعه رفتار آشوبی یک نوسان‌ساز مکانیکی در می‌یابیم، می‌توانیم سریعاً برای درک رفتار آشوبی سایر سیستم‌ها به کار ببریم.

ویژگی‌های یک سیستم آشوبی

سیستم‌های دینامیکی آشوبی مشخصه‌های زیر را دارند:

1. نسبت به شرایط اولیه حساس هستند.
2. چرخش متناوب آن‌ها متراکم است.
3. از نظر توپولوژیکی با هم ترکیب می‌شوند.

حساسیت به شرایط اولیه به این معنی است که یک اغتشاش کوچک در مسیر فعلی ممکن است منجر به رفتار بسیار متفاوت در آینده شود. ترکیب توپولوژیکی نیز بدین معناست که با گذشت زمان، سیستم به طوری تکامل می‌یابد که هر ناحیه یا مجموعه باز از فضای فاز آن، در نهایت با هر ناحیه معین دیگری همپوشانی داشته باشد.

دینامیک غیرخطی و آشوب

واژه آشوب اصطلاحی است که برای توصیف رفتار پیچیده سیستم‌های دینامیکی به کار می‌رود. آشوب در حقیقت یکی از انواع رفتارهای این سیستم‌ها است. زیرهمساز و شبه‌تناوب از انواع دیگر رفتارها در این سیستم‌ها هستند. این شاخه از علم به طور عمومی‌تر «دینامیک غیرخطی» (Nonlinear Dynamics) نامیده می‌شود که در آن، رفتار دینامیکی (یعنی رفتار زمانی) یک سیستم غیرخطی بررسی می‌شود. یک سیستم غیرخطی سیستمی است که معادله‌های زمانی آن (معادلات دیفرانسیل) غیرخطی هستند، یعنی متغیر در معادله به فرم غیرخطی ظاهر می‌شود. سیستم‌های غیرخطی همواره نقش مهمی در مطالعه پدیده‌های طبیعی ایفا می‌کنند و در دهه‌های اخیر تحقیقات گسترده‌ای درباره آن‌ها انجام شده است.

دلیل اصلی این رشد تحقیقات، امکان محاسبات قدرتمند و کم‌هزینه است. برخلاف سیستم‌های خطی که جواب‌هایی به فرم بسته دارند، تعداد کمی از سیستم‌های غیرخطی جوابی به فرم بسته دارند و به همین دلیل روش‌های عددی نقش مهمی در فرایند یافتن و تحلیلی پدیده‌های غیرخطی دارند. قبل از ظهور رایانه‌های کم‌هزینه، فقط برخی از پژوهشگران امکان انجام شبیه‌سازی‌های غیرخطی را داشتند. امروزه، هر کسی با یک رایانه شخصی می‌تواند یک سیستم غیرخطی را شبیه‌سازی کند.

یکی از اصول ابتدایی علم این است که سیستم‌های قطعی قابل پیش‌بینی هستند، یعنی برای شرایط اولیه داده شده و معادلات توصیف کننده سیستم، برای همه زمان‌ها می‌توان رفتار سیستم را پیش‌بینی کرد. کشف سیستم‌های سیستم‌های آشوبی این دیدگاه را نقض کرد. به بیان ساده‌تر، یک سیستم آشوبی سیستمی قطعی است که رفتار تصادفی دارد. آشوب رفتار «عجیب» یا «شگفت» (Strange) نیز نامیده می‌شود و یکی از موضوعات بسیار جذاب در پژوهش سیستم‌های غیرخطی است.

غیرخطی بودن و آشوب

اگر یک سیستم دینامیکی رفتار آشوبی از خود نشان دهد، غیرخطی خواهد بود. عنصر اصلی برای درک آشوب مفهوم غیرخطی بودن است. دینامیک غیرخطی به مطالعه سیستم‌هایی می‌پردازد که در آن‌ها معادلات غیرخطی هستند. همه سیستم‌های واقعی، حداقل تا حدودی غیرخطی هستند.

برخی از تغییرات ناگهانی و چشمگیر در سیستم‌های غیرخطی ممکن است رفتار پیچیده‌ای به نام آشوب ایجاد کند. کلمات آشوب و آشوبی (آشوبناک) برای توصیف رفتار زمانی یک سیستم استفاده می‌شود که رفتار آن نادوره‌ای است (هرگز به طور کامل تکرار نمی‌شود) و «ظاهراً» تصادفی یا نویزی است. در پس این تصادفی بودن آشوبی، نظمی وجود دارد که توسط معادلات سیستم تعیین می‌شود. در واقع، بسیاری از سیستم های آشوبی کاملاً قطعی هستند.

سیستمی را قطعی می‌گوییم که رفتارهای بعدی سیستم به طور کامل قابل تعیین باشند، یعنی سیستمی که در آن، حالت‌های بعدی از موارد قبلی پیروی می‌کند یا توسط آن‌ها تعیین می‌شود. چنین سیستمی در مقابل «سیستم تصادفی» است که در آن حالت‌های آینده از حالت‌های قبلی مشخص نمی‌شوند.

اگر یک سیستم قطعی باشد، لزوماً به این معنی نیست که حالت‌های بعدی آن با آگاهی از موارد قبلی قابل پیش‌بینی هستند. به این ترتیب، آشوب مشابه یک سیستم تصادفی است. به عنوان مثال، آشوب «آشوب قطعی» نامیده می‌شود، زیرا اگرچه توسط قوانین ساده تعیین می‌شود، اما خاصیت وابستگی حساس آن به شرایط اولیه باعث می‌شود که یک سیستم آشوبی، در عمل، تا حد زیادی غیرقابل پیش‌بینی باشد. از این رو، رفتار غیرقابل پیش‌بینی سیستم قطعی «آشوب» نامیده می‌شود. هسته اصلی مسئله هماهنگ کردن این قطعیت با تصادفی بودن ظاهری است.

کمی‌سازی آشوب

تعیین تصادفی یا آشوبی بودن یک سیستم یا فرایند فیزیکی از روی داده‌ها کار دشواری است، زیرا در عمل هیچ سری زمانی از «سیگنال خالص» تشکیل نشده است. همیشه نوعی نویز مزاحم وجود دارد، حتی اگر خطای گرد کردن باشد. بنابراین، هر سری زمانی حقیقی حتی اگر غالباً قطعی باشد، مقداری تصادفی بودن خواهد داشت.

ریاضی‌دانان روش‌های دیگری را برای کمی‌سازی توصیف سیستم‌های آشوبی بیان کرده‌اند. این روش‌ها عبارتند از: بعد فراکتالی جاذب، نماهای لیاپانوف، نمودارهای تکرارشونده، نگاشت‌های پوانکاره، نمودارهای انشعاب یا دوشاخگی و عملگر انتقال.

معادله لجستیک

معادله لجستیک که «مدل ورهاست» (Verhulst Model) نیز نام دارد، به صورت زیر است:

$$\large x _ { n + 1 } = r x _ n ( 1 - x _ n )$$

که در آن، $$r$$ پارامتری است که نرخ رشد را نشان می‌دهد و $$x _ n$$ متغیر در تکرار $$n$$اُم و $$n$$ متغیر اجرا است. این معادله، یک مدل رشد جمعیت است که که اولین بار توسط پییر فرانسوا ورهاست (Pierre François Verhulst) منتشر شد. نسخه گسسته معادله لجستیک، به عنوان «نگاشت لجستیک» (Logistic Map) شناخته می‌شود. نگاشت لجستیک، یک تصویر (Mapping) چندجمله‌ای است که اغلب به عنوان نمونه‌ای برای نشان دادن این موضوع به کار می‌رود که چگونه یک رفتار پیچیده آشوبی می‌تواند از معادلات دینامیکی غیرخطی ساده ناشی شود (تابع $$f$$ در فضای فاز حالت بعدی $$z$$، یعنی $$f(z)$$ (تصویر) را به دست می‌دهد. این گفته را می‌توان به صورت $$z'=f ( z)$$ نوشت که در آن، علامت پریم به معنای نقطه بعدی است).

نگاشت لجستیک یک نگاشت وارون‌ناپذیر است؛ یعنی می‌توان آن را در زمان رو به جلو تکرار کرد و از $$x _ n$$ به یک $$x _{n+1}$$ رسید، اما عکس این عمل شدنی نیست. این نگاشت، تابع نگاشت تکرارشونده نیز نامیده می‌شود، زیرا یک مقدار $$x$$ به نام $$x _ 0$$ را به مقدار دیگری از آن به نام $$x _ 1$$ می‌نگارد. با انجام مداوم تکرارها نگاشت لجستیکی رفتارهای متنوعی را نشان خواهد داد. دنباله جواب‌های تکرارشونده یک مسیر یا مدار نامیده می‌شود.

نمودار انشعاب نگاشت لجستیک

انشعاب یا دوشاخگی (Bifurcation)، یک تغییر کیفی در دینامیکی است که در اثر تغییر یک پارامتر سیستم رخ می‌دهد. یک نمودار دوشاخگی، مقادیر طولانی مدت ممکن یک متغیر از یک سیستم را نشان می‌دهد که می‌توان آن را به عنوان تابعی از پارامتر سیستم به دست آورد. یک مثال، نمودار انشعاب نگاشت لجستیک است. در این حالت، پارامتر $$r$$ روی محور افقی شکل نشان داده شده و محور عمودی تراکم مقادیر جمعیت دراز مدت مربوط به تابع لجستیک را نشان می‌دهد.

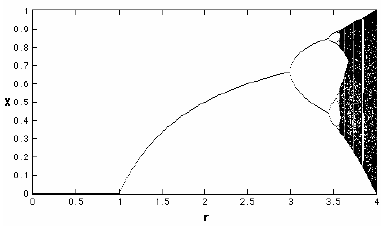
شکل بالا نشان می‌دهد که برای $$r$$های کوچک‌تر از ۱، همه نقاط به صفر نگاشته می‌شوند. صفر جاذب یک نقطه برای $$r$$های کوچک‌تر از یک است. برای $$r$$های بین ۱ تا ۳، هنوز جاذب‌های تک‌نقطه‌ای داریم. این مقدار جذب شده $$x$$ با افزایش $$r$$ به حداقل $$r = 3$$ افزایش می‌یابد. انشعابات در $$r = 3$$، $$r = 3.45$$، $$r = 3.54$$، $$r = 3.564$$، $$r = 3.569$$ و... تا زیر $$3.57$$ (که در آن، چند نوسان متناوب ناپایدار وجود دارد که همان رفتار آشوبی است) رخ می‌دهد. یک تغییر کوچک در $$r$$ ممکن است به یک سیستم آشوبی پایدار بسازد و برعکس. این دنباله، دو برابر شدن تناوب مسیر آشوب نام دارد.

دنباله دو برابر شدن دوره در طی انشعاب (جدا شدن به دو بخش) نقاط ثابت قبل (وقتی ناپایدار می‌شوند) رخ می‌دهد. این موضوع به خوبی شکل‌گیری تناوب‌های ممکن چرخه‌های پایدار را از ۱ به ۲ به ۴ به ۸ و... نشان می‌دهد. این جدا شدن و بریدگی به عنوان «انشعاب چنگالی» (Pitchfork Bifurcation) شناخته می‌شود. در هر نقطه انشعاب دو برابر دوره تناوب، نقطه ثابت دوره‌ای پایدار قبلی ناپایدار شده و دو نقطه ثابت پایدار ادغام می‌شوند. این معادله مشخص می‌کند که چگونه سیستم‌های قطعی (خروجی‌های پایدار)، هنگامی که تحت فشار قرار می‌گیرند، می‌توانند خروجی‌های غیرقابل پیش‌بینی و آشوبی تولید کنند. برای مقادیر بزرگ‌تر $$r$$ ($$3.5$$ تا $$4$$) سیستم وابستگی حساسی به شرایط اولیه نشان می‌دهد؛ یعنی تغییرات جزئی در مقدار $$r$$ منجر به خروجی‌های بسیار متفاوتی خواهد شد.

یک ویژگی جالب این نمودار این است که وقتی تناوب به بی‌نهایت می‌رود، $$r$$ محدود باقی می‌ماند. هنگامی که $$r$$ بزرگ‌تر از تقریباً $$3.57$$ باشد، مدارها (چرخه‌ها) آشوبی می‌شوند. بنابراین، این نمودار انشعاب یک مثال خوب برای بیان اهمیت نظریه آشوب حتی در سیستم‌های غیرخطی بسیار ساده است. نمودار انشعاب یک ابزار اساسی برای مطالعه تغییر رفتار سیستم در پاسخ به تغییرات پارامترهای سیستم است.

جاذب‌ها

مدار نگاشت لجستیک از طریق تکرارهای مکرر به سمت مداری که یا دوره‌ای است یا آشوبی جذب می‌شود. جاذب (Attractor) مجموعه‌ای از نقاط است که وقتی تعداد تکرارها افزایش می‌یابد، به مدار نزدیک می‌شود؛ یعنی یک جواب متعادل (تعادل) است که سیستم به آن همگرا می‌شود. اگر سیستم به یک مدار یا چرخه تناوبی برسد، آنگاه می‌گوییم، یک «جاذب دوره‌ای» (Periodic Attractor) داریم. برای مثال، جاذب دوره‌ای-۱، جاذب دوره‌ای-۲، جاذب دوره‌ای-۴ و... . از سوی دیگر، اگر سیستم با یک مدار نادوره‌ای به صورت آشوبی عمل کند، آنگاه یک «جاذب آشوبی» (Chaotic Attractor) داریم که به اغلب با نام «جاذب شگفت» (Strange Attractor) نیز شناخته می‌شود.

یک جاذب عجیب شامل تعداد بی‌نهایتی از نقاط کران‌دار در ناحیه مشخصی از فضای حالت است (یک جاذب با بعد فراکتالی) و رفتار منتجه آشوب نامیده می‌شود. این آشوب یک رفتار نادوره‌ای کران‌دار از یک سیستم است. به طور خلاصه، جاذب‌ها رأس و مبداء آشوب هستند.

لورنتس اولین فردی بود که با یک جاذب عجیب مواجه شد و متوجه شد که برای محدوده‌های خاصی از یک پارامتر، مسیرها از شرایط اولیه بسیار نزدیک به هم شروع می‌شوند و سریع حرکت می‌کنند و منجر به حالت‌های کاملاً متفاوتی در آینده می‌شوند. این موضوع «وابستگی حساس به شرایط اولیه» نامیده می‌شود که مشخصه آشوب و ویژگی اصلی سیستم‌های آشوبی است.

این حساسیت مفهوم بسیار مهمی دارد. بخش عمده‌ای از مطالعه سیستم‌های دینامیکی ضرورتاً به پیش‌بینی حالت‌های آینده سیستم منجر می‌شود. اما حساسیت به شرایط اولیه در سیستم های آشوبی، پیش‌بینی در مدت زمان کوتاه را غیرممکن می‌کند. دلیل این امر آن است که نمی‌توان شرایط اولیه را با دقت نامتناهی اندازه‌ گرفت یا مشخص کرد.

خطاهای کوچک در تعریف شرایط اولیه سیستم‌های دوره‌ای پایدار اهمیتی ندارند، زیرا مدارهایی که از شرایط اولیه کمی متفاوت شروع می‌شوند، به صورت نمایی تغییر نمی‌کنند. اما در یک جاذب آشوبی، حالت‌های به طور دلخواه نزدیک به صورت نمایی واگرا می‌شوند و پیش‌بینی غیرممکن می‌شود، مگر اینکه شرایط اولیه با اطلاعات نامحدود شناخته شده و با دقت نامحدود مشخص شود که امری غیرممکن است. به طور خلاصه، دو نقطه شروع نزدیک به هم می‌توانند به دو مسیر کاملاً متفاوت تبدیل شوند. از این رو، حتی اگر سیستم قطعی باشد، حالت نهایی غیرقابل پیش بینی است.

نظریه آشوب از دیدگاه ریاضی

در اغلب کتاب‌ها، نظریه آشوب با موضوعی به نام معادله لجستیک آغاز می‌شود. وقتی این معادله غیرخطی (در حقیقت درجه دوم) تکرار شود، رفتار بسیار پیچیده‌ای دارد. معادله لجستیک، اغلب در مدلسازی رشد جمعیت و سایر فرایندها مورد استفاده قرار می‌گیرد. برای توضیح آشوب از معادلات ساده‌تری استفاده می‌کنیم. در اینجا می‌خواهیم از دیدگاه ریاضی به بررسی آشوب بپردازیم.

با یک معادله خطی ساده به فرم زیر شروع می‌کنیم:

$$\large y = x - 1$$

در معادله بالا، دو متغیر با نام‌های $$x$$ و $$y$$ داریم. متغیر $$x$$، متغیر مستقل نامیده می‌شود و $$y$$ متغیر وابسته است. بدین ترتیب، متغیر $$x$$ را جایگذاری کرده و مقدار $$y$$ متناظر با آن را به دست می‌آوریم. برای مثال، وقتی از مقدار $$x = 0$$ استفاده می‌کنیم، مقدار $$y = 0 - 1 = -1$$ به دست می‌آید. به طور مشابه، با قرار دادن $$x = 1$$، از معادله بالا مقدار $$y = 1 - 1 = 0$$‌ را به دست می‌آوریم.

اکنون می‌خواهیم بررسی کنیم مجموعه‌ای از عملیات تکراری با استفاده از معادله بالا که فرایند تکرار (Process of Iteration) نامیده می‌شود، چگونه است. از مقدار اولیه $$x$$ شروع می‌کنیم، آنگاه مقدار $$y$$‌ را به دست می‌آوریم. سپس از مقدار جدید $$y$$ برای جایگذاری در معادله برای $$x$$ به منظور به دست آوردن یک مقدار دیگر $$y$$ استفاده می‌کنیم. همین عملیات را ادامه می‌دهیم، یعنی هر مقدار به دست آمده را چندین بار در معادله جایگذاری می‌کنیم. به عنوان یک مثال مشخص، با در نظر گرفتن یک مقدار اولیه برای $$x$$، عملیات را ۱۰ بار تکرار می‌کنیم. اما قبل از انجام این کار، برای سادگی، نمادگذاری‌ها را کمی تغییر می‌دهیم. از آنجایی که در هر تکرار از یک مقدار جدید برای $$x$$ استفاده می‌کنیم، مقدار فعلی آن را با $$x ( n )$$ مشخص می‌کنیم و مقدار جدید را که به دست می‌آوریم، $$x (n+1)$$ می‌نامیم. مقادیر پارامتر $$n$$، اعداد ۰ تا ۱۰ هستند.

بنابراین، مقدار اولیه برای شروع تکرار، $$x ( 0 )$$ است. مقادیر بعدی نیز $$x ( 1)$$ تا $$x ( 10 )$$ خواهند بود. این مقادیر را که تکرار نامیده می‌شوند، برای مقدار اولیه $$x ( 0 ) = 0.2673$$ محاسبه می‌کنیم. تکرارها به صورت زیر خواهند بود:

$$\large \begin {align*} x ( 1 ) & = x ( 0 ) - 1 = 0.2673 - 1 = -0.7327 \\ x ( 2) & = x ( 1 ) - 1 = -0.7327 - 1 = -1.7327 \\ x ( 3 ) & = x ( 2 ) - 1 = -1.7327 - 1 = -2.7327 \\ x ( 4 ) & = x ( 3 ) - 1 = -2.7327 - 1 = -3.7327 \\ x ( 5 ) & = x ( 4 ) - 1 = -3.7327 - 1 = -4.7327 \\ x ( 6 ) & = x ( 5 ) - 1 = -4.7327 - 1 = -5.7327 \\ x ( 7 ) & = x ( 6 ) - 1 = -5.7327 - 1 = -6.7327 \\ x ( 8 ) & = x ( 7 ) - 1 = -6.7327 - 1 = -7.7327 \\ x ( 9 ) & = x ( 8 ) - 1 = -7.7327 - 1 = -8.7327 \\ x ( 10 ) & = x ( 9 ) - 1 = -8.7327 - 1 = -9.7327 \end {align*}$$

برای آنکه بفهمیم در این معادله (یا فرایند) آشوب وجود دارد، باید فرایند تکرار بالا را با تغییر اندکی در شرایط اولیه تکرار کنیم. بنابراین، شرایط اولیه مثال را به اندازه کوچک $$0.0001$$ تغییر می‌دهیم؛ یعنی شرایط اولیه جدید را $$0.2674$$ در نظر می‌گیریم. اکنون ۱۰ تکرار را برای این مقدار اولیه به صورت زیر انجام می‌دهیم:

$$\large \begin {align*} x ( 1 ) & = x ( 0 ) - 1 = 0.2674- 1 = -0.7326\\ x ( 2) & = x ( 1 ) - 1 = -0.7326 - 1 = -1.7326 \\ x ( 3 ) & = x ( 2 ) - 1 = -1.7326 - 1 = -2.7326 \\ x ( 4 ) & = x ( 3 ) - 1 = -2.7326 - 1 = -3.7326 \\ x ( 5 ) & = x ( 4 ) - 1 = -3.7326 - 1 = -4.7326 \\ x ( 6 ) & = x ( 5 ) - 1 = -4.7326 - 1 = -5.7326 \\ x ( 7 ) & = x ( 6 ) - 1 = -5.7326 - 1 = -6.7326 \\ x ( 8 ) & = x ( 7 ) - 1 = -6.7326 - 1 = -7.7326 \\ x ( 9 ) & = x ( 8 ) - 1 = -7.7326 - 1 = -8.7326 \\ x ( 10 ) & = x ( 9 ) - 1 = -8.7326 - 1 = -9.7326 \end {align*}$$

با مقایسه تکرارهای بالا برای معادله ساده $$y = x - 1$$، می‌بینیم که وقتی شرایط اولیه به اندازه کم $$0.0001$$ تغییر می‌کند، نتیجه نهایی پس از 10 تکرار نیز به اندازه اندکی ($$0.0001$$) تغییر خواهد کرد. این تغییر کوچک در نتیجه نهایی عادی و قابل پیش‌بینی خواهد بود. بنابراین، می‌توانیم بگوییم که در این مثال، آشوب ظاهر نشده است.

بنابراین، می‌توان گفت معادله ساده $$y = x - 1$$، وقتی که تکرار می‌شود، رفتار آشوبی ندارد. در ادامه نشان خواهیم داد که اگر از یک معادله خطی ساده دیگر با کمی تغییر استفاده کنیم، رفتار آشوبی قابل توجهی ظاهر خواهد شد.

بنابراین، اکنون معادله زیر را در نظر می‌گیریم و با همان شرایط اولیه قبلی تکرارها را انجام می‌دهیم:

$$\large y = 2x - 1$$

 برای مقدار اولیه $$0.2673$$، ده تکرار به صورت زیر است:

$$\large \begin {align*} x ( 1 ) & = 2 x ( 0 ) - 1 = 2 ( 0.2673 ) - 1 = -0.4654\\ x ( 2 ) & = 2 x ( 1 ) - 1 = 2 ( -0.4654 ) - 1 = - 1.9308 \\ x ( 3 ) & = 2 x ( 2 ) - 1 = 2 ( - 1.9308 ) - 1 = - 4.8616 \\ x ( 4 ) & = 2 x ( 3 ) - 1 = 2 ( - 4.8616 ) - 1 = -10.7232 \\ x ( 5 ) & = 2 x ( 4 ) - 1 = 2 ( -10.7232 ) - 1 = - 22.4464 \\ x ( 6 ) & = 2 x ( 5 ) - 1 = 2 ( - 22.4464 ) - 1 = - 45.8928 \\ x ( 7 ) & = 2 x ( 6 ) - 1 = 2 ( - 45.8928 ) - 1 = - 92.7856 \\ x ( 8 ) & = 2 x ( 7 ) - 1 = 2 ( - 92.7856 ) - 1 = - 186.5712 \\ x ( 9 ) & = 2 x ( 8 ) - 1 = 2 ( - 186.5712 ) - 1 = - 374.1424 \\ x ( 10 ) & = 2 x ( 9 ) - 1 = 2 ( - 374.1424 ) - 1 = - 749.2848 \end {align*}$$

برای آنکه پی ببریم در این معادله آشوب وجود دارد یا نه، باید فرایند تکرار بالا را به ازای تغییر اندکی در شرایط اولیه انجام دهیم. بدین منظور، مقدار اولیه $$0.2674$$ را در نظر می‌گیریم. در این صورت، تکرارها به صورت زیر هستند:

 $$\large \begin {align*} x ( 1 ) & = 2 x ( 0 ) - 1 = 2 ( 0.2674 ) - 1 = -0.4652\\ x ( 2 ) & = 2 x ( 1 ) - 1 = 2 ( -0.4652 ) - 1 = - 1.9304 \\ x ( 3 ) & = 2 x ( 2 ) - 1 = 2 ( - 1.9304 ) - 1 = - 4.8608 \\ x ( 4 ) & = 2 x ( 3 ) - 1 = 2 ( - 4.8608 ) - 1 = -10.7216 \\ x ( 5 ) & = 2 x ( 4 ) - 1 = 2 ( -10.7216) - 1 = - 22.4432 \\ x ( 6 ) & = 2 x ( 5 ) - 1 = 2 ( - 22.4432 ) - 1 = - 45.8864 \\ x ( 7 ) & = 2 x ( 6 ) - 1 = 2 ( - 45.8864 ) - 1 = - 92.7728 \\ x ( 8 ) & = 2 x ( 7 ) - 1 = 2 ( - 92.7728 ) - 1 = - 186.5456 \\ x ( 9 ) & = 2 x ( 8 ) - 1 = 2 ( - 186.5456 ) - 1 = - 374.0912 \\ x ( 10 ) & = 2 x ( 9 ) - 1 = 2 ( - 374.1424 ) - 1 = - 749.1824 \end {align*}$$

با مقایسه دو تکرار اخیر برای معادله خطی ساده $$y = 2 x - 1$$، مشاهده می‌کنیم که وقتی مقدار اولیه به اندازه کمی (از $$0.2673$$ تا $$0.2674$$) تغییر کند، نتیجه نهایی پس از تکرارها از $$-749.2848$$ به $$-749.1824$$ تغییر می‌کند که تغییر قابل توجهی نسبت به تغییرات مقدار اولیه است. این تغییر نسبتاً قابل توجه در نتیجه نهایی مورد انتظار نبود و اصلاً انتظار آن را نداشتیم. بنابراین، می‌توان گفت که در این مثال، پدیده آشوب ظاهر شده است.

در نتیجه، وقتی معادله $$y = 2 x - 1$$ تکرار می‌شود، رفتار آشوبی دارد. در واقع، می‌توان گفت که هرچه تعداد تکرارها بیشتر شود و مثلاً به 100 یا 1000 بار برسد، نتایج کاملاً متفاوتی به دست خواهیم آورد. این همان ماهیت آشوب است.

پرسشی که اکنون باید به آن پاسخ دهیم، این است که چرا معادله $$y = 2 x - 1$$ با فرایند تکرار رفتار آشوبی دارد، اما معادله $$y = x - 1$$ رفتار آشوبی از خود نشان نمی‌دهد. برای آنکه به این پرسش پاسخ دهیم، مشخصه‌‌های هر یک از دو معادله را به صورت جدا آزمایش می‌کنیم.

چند تکرار نخست معادله $$y = x - 1$$ بدون استفاده از اعداد به صورت زیر است:

$$\large \begin {align*} x ( 1 ) & = x ( 0 ) - 1 \\ x ( 2 ) & = x ( 1 ) - 1 = ( x ( 0 ) - 1 ) -1 = x ( 0 ) - 2 \\ x ( 3 ) & = x ( 2 ) - 1 = ( x ( 0 ) - 2 ) - 1 = x ( 0 ) - 3 \\ x ( 4 ) & = x ( 3 ) - 1 = ( x ( 0 ) - 3 ) - 1 = x ( 0 ) - 4 \end {align*}$$

حال اگر تکرارهای بالا را $$n$$ بار ادامه دهیم، خواهیم داشت:

$$\large x ( n ) = x ( 0 ) - n$$

معادله بالا، یک معادله صریح برای تکرار $$n$$اُم $$x$$ است. حال بررسی می‌کنیم که با اندکی تغییر در مقدار اولیه $$x ( 0 )$$ چه اتفاقی در نتیجه نهایی رخ می‌دهد. بدین منظور، شرایط اولیه $$x (0) + \varepsilon$$ را در نظر می‌گیریم که در آن، $$\varepsilon$$ یک عدد بسیار کوچک است. تکرار را برای این شرایط اولیه جدید، $$x ( m )$$‌ می‌نامیم ($$m$$اُمین تکرار). براساس معادله بالا، عبارت زیر را برای شرایط اولیه جدید خواهیم داشت:

$$\large x ( m ) = ( x ( 0 ) + \varepsilon ) - m = x ( 0 ) + \varepsilon - m$$

با تفریق دو معادله از هم، داریم:

$$\large x ( m ) - x ( n ) = (x ( 0 ) + \varepsilon - m ) - (x ( 0) - n ) = \varepsilon + n - m$$

برای اینکه ببینیم این معادله آشوبی است یا خیر، مقدار $$m = n$$ را قرار می‌دهیم و داریم:

$$\large x ( n ) - x ( n ) = \varepsilon + n - n = \varepsilon$$

و از آنجایی که $$\varepsilon$$ یک عدد بسیار کوچک است، معادله بالا با افزایش مقدار $$n$$ به صفر میل می‌کند. بنابراین، در این حالت، با افزایش $$n$$ و $$m$$ به بی‌نهایت، مقدار $$x(n)$$ و $$x(m)$$ برابر خواهند شد.

اکنون مشابه عملیات بالا را برای معادله $$y = 2x - 1$$ انجام می‌دهیم. بنابراین، تکرارهای زیر را داریم:

$$\large \begin {align*} x ( 1 ) & = 2 x ( 0 ) - 1 \\ x ( 2 ) & = 2 x ( 1 ) - 1 = 2 ( 2 x ( 0 ) - 1 ) -1 = 2 ^ 2 x ( 0 ) - 2 - 1 \\ x ( 3 ) & = 2 x ( 2 ) - 1 = 2 (2 ^ 2 x ( 0 ) - 2 -1 ) - 1 = 2 ^ 3 x ( 0 ) - 2 ^ 2 - 2 - 1 \\ x ( 4 ) & = 2 x ( 3 ) - 1 = 2 (2 ^ 3 x ( 0 ) - 2^ 2 -2 -1 ) - 1 = 2 ^ 4 x ( 0 ) - 2 ^ 3 - 2 ^ 2 - 2 - 1 \\ \end {align*}$$

اگر تکرار بالا را $$n$$ بار انجام دهیم، خواهیم داشت:

$$\large x ( n ) = 2 ^ n x ( 0 ) - 2 ^ {n-1} - 2 ^ {n-2} - 2 ^ {n - 3 } - \cdots - 1$$

معادله بالا را می‌توان به شکل زیر بازنویسی کرد:

$$\large x ( n ) = 2 ^ n x ( 0 ) - ( 1 + 2 + 2 ^ 2 + \cdots + 2 ^ { n - 3 } + 2 ^ { n -2} + 2 ^ {n - 1 } )$$

عبارت داخل پرانتز در معادله بالا یک سری هندسی است و می‌توان آن را به صورت زیر نوشت:

$$\large 1 + 2 + 2 ^ 2 + \cdots + 2 ^ { n - 3 } + 2 ^ { n -2} + 2 ^ {n - 1 } = \frac { 2 ^ n - 1 } {2 - 1 } = 2 ^ n - 1$$

بنابراین، $$x ( n )$$ برابر است با:

$$\large x ( n ) = 2 ^ n x ( 0 ) - ( 2 ^ n - 1 )$$

معادله بالا، یک معادله صریح برای تکرار $$n$$اُم $$x$$ است. اکنون شرایط اولیه را کمی تغییر می‌دهیم و آن را به صورت $$x ( 0 ) + \varepsilon$$ می‌نویسیم که در آن، $$\varepsilon$$ یک عدد بسیار کوچک است. حال، تکرار $$m$$اُم را محاسبه می‌کنیم. بنابراین، داریم:

$$\large x ( m ) = 2 ^ m ( x ( 0 ) + \varepsilon ) - ( 2 ^ m - 1 )$$

با تفریق دو معادله از یکدیگر، می‌توان نوشت:

$$\large x ( m ) - x ( n ) = [ 2 ^m (x ( 0 ) + \varepsilon ) - ( 2 ^m - 1 ) ] - [ 2 ^n x ( 0 ) - ( 2 ^ n - 1 ) ]$$

پس از ساده‌سازی، داریم:

$$\large x ( m ) - x ( n ) = ( 2 ^ m - 2 ^ n ) x ( 0 ) + 2 ^ m \varepsilon + 2 ^ n - 2 ^ m$$

برای بررسی آشوبی بودن این معادله خطی مورد نظر، تساوی $$m = n$$ را در نظر می‌گیریم و در نتیجه، خواهیم داشت:

$$x ( n ) - x ( n ) = 2 ^ n \varepsilon$$

همان‌طور که می‌دانیم، $$\varepsilon$$ یک عدد بسیار کوچک است، اما معادله بالا با افزایش مقدار $$n$$ به سمت صفر میل نمی‌کند. این به دلیل ظاهر شدن ضریب $$2 ^ n$$ در نتیجه نهایی است. در واقع، با افزایش $$n$$، این عبارت به بی‌نهایت میل می‌کند. بنابراین، در این حالت، به ازای افزایش $$n$$ و $$m$$‌ به بی‌نهایت، نتایج یکسانی برای $$x ( n )$$ و $$x ( m )$$ نخواهیم داشت. در نتیجه، این معادله رفتار آشوبی دارد.

با مقایسه دو معادله خطی، مشاهده می‌کنیم که وقتی ضرایب $$x$$ بزرگ‌تر از ۱ باشند، آنگاه آشوب اتفاق می‌افتد. البته وقتی ضریب $$x$$ برابر با یک باشد، آشوب رخ نخواهد داد. این به آن دلیل است که بدون توجه به مقدار پارامتر $$\varepsilon$$، تساوی $$1 ^ \varepsilon = 1$$ را داریم. واضح است که وقتی ضریب ۲ و بزرگ‌تر از آن باشد، چنین چیزی رخ نخواهد داد. حال این پرسش پیش می‌آید که برای معادلاتی با ضرایب کوچک‌تر از ۱ چه اتفاقی می‌افتد؟

معادله خطی $$y = \frac { 1 } { 2 } x - 1$$ را در نظر بگیرید که در آن، ضریب $$x$$ کمتر از ۱ است. در این حالت، با تکرار محاسباتی که در بالا برای حالت‌های دیگر انجام دادیم، تکرار $$n$$اُم به مقدار $$(\frac {1}{2} ) ^ n \varepsilon$$ می‌رسد که در آن، $$\varepsilon$$ یک عدد بسیار کوچک است. واضح است که با افزایش $$n$$، مقدار مذکور به صفر میل می‌کند. بنابراین، برای معادله خطی، آشوب وجود ندارد. در حالت کلی، در یک معادله خطی، وقتی ضریب $$x$$ کمتر از ۱ باشد، رفتار آشوبی نخواهیم داشت.

در ادامه، می‌خواهیم بررسی کنیم که وقتی تکرار را همزمان برای چند معادله خطی انجام دهیم، چه اتفاقی خواهد افتاد. برای سادگی، دستگاه معادلات خطی زیر را در نظر بگیرید:

$$\large \begin {cases} x _ { n + 1 } = 2 x _ n + y _ n + 1 \\ y _ { n + 1 } = x _ n + 2 y _ n + 2 \end {cases}$$

دستگاه معادلات بالا را می‌توان به فرم ماتریسی زیر نوشت:

$$\large \left \{ \begin{matrix} x _ { n + 1 } \\ y _ { n + 1 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} x _ { n } \\ y _ { n } \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

برای بررسی وجود یا عدم وجود رفتار آشوبی، تکرار را چند بار برای دستگاه فوق انجام می‌دهیم. با شروع از شرایط اولیه، تکرار اول به صورت زیر خواهد بود:

$$\large \left \{ \begin{matrix} x _ { 1 } \\ y _ { 1 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

نتیجه تکرار دوم نیز به صورت زیر است:

$$\large \left \{ \begin{matrix} x _ { 2 } \\ y _ { 2 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} x _ { 1 } \\ y _ { 1 } \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

با جایگذاری مقادیر تکرار اول در معادله بالا، داریم:

$$\large \left \{ \begin{matrix} x _ { 2 } \\ y _ { 2 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left ( \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \} \right ) + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

با ساده‌سازی معادله فوق، خواهیم داشت:

$$\large \left \{ \begin{matrix} x _ { 2 } \\ y _ { 2 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}^ 2 \left \{ \begin{matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

با ادامه روند فوق، برای تکرار سوم داریم:

$$\large \left \{ \begin{matrix} x _ { 3 } \\ y _ { 3 } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}^ 3 \left \{ \begin{matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ^2 \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}+ \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

در حالت کلی، فرمول زیر را برای تکرار $$n$$اُم داریم:

$$\large \left \{ \begin{matrix} x _ { n } \\ y _ { n } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}^ n \left \{ \begin{matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ^{n-1} \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}+ \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ^ { n - 2} \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \} + \cdots + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \} + \left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

اکنون معادله بالا را به فرم ساده شده زیر بازنویسی می‌کنیم:

$$\large \left \{ \begin {matrix} x _ { n } \\ y _ { n } \end {matrix} \right \} = \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}^ n \left \{ \begin {matrix} x _ { 0 } \\ y _ { 0 } \end {matrix} \right \} + \left ( \begin {bmatrix} 2 & 1 \\ 1 & 2 \end {bmatrix} ^{n-1} + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ^ { n - 2} + \cdots + \begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} + \begin {bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right )\left \{ \begin{matrix} 1 \\ 2 \end {matrix} \right \}$$

عبارت داخل پرانتز یک سری هندسی به فرم زیر است:

$$\large [A ] ^ { n -1} + [ A ] ^ { n - 2 } + \cdots + [ I ]$$

برای ساده کردن عبارت بالا، باید از اتحاد ریاضی زیر استفاده کنیم:

$$\large ([A ] ^ { n -1} + [ A ] ^ { n - 2 } + \cdots + [ I ]) ([I]- [ A ] ) = [ I ] - [ A ] ^ n$$

بنابراین، $$n$$اُمین تکرار دستگاه معادلات خطی به صورت زیر خواهد بود:

$$\large \left\{ \begin {array} { l } { x _ { n } } \\ { y _ { n } } \end {array} \right\} = \left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { n } \left\{\begin {array} {l } { x _ { 0 } } \\ { y _ { 0 } } \end {array} \right\} + \left ( \left[ \begin {array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right] - \left[ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { n } \right ) \left ( \left [ \begin {array} { l l } { 1} & { 0 } \\ { 0 } & { 1 } \end {array} \right ] - \left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right ] \right ) ^ { - 1 } \left\{ \begin {array} { l } { 1 } \\ { 2 } \end {array} \right\}$$

معادله بالا یک معادله صریح برای تکرار $$n$$اُم $$\left \{ \begin {matrix} x \\ y \end {matrix} \right \}$$ است. اکنون می‌خواهیم بررسی کنیم که با تغییر کوچک شرایط اولیه $$\left \{ \begin {matrix} x ( 0 ) \\ y ( 0) \end {matrix} \right \}$$ چه اتفاقی رخ می‌دهد. بدین منظور، شرایط اولیه $$\left \{ \begin {matrix} x ( 0 ) + \varepsilon \\ y ( 0) + \delta \end {matrix} \right \}$$ را در نظر بگیرید که در آن، $$\varepsilon$$ و $$\delta$$ اعداد بسیار کوچکی هستند. اکنون تکرار جدید را $$\left \{ \begin {matrix} x _ m \\ y _ m \end {matrix} \right \}$$ می‌نامیم ($$m$$اُمین تکرار). بر اساس معادله بالا، می‌توانیم عبارت زیر را برای تکرار $$m$$اُم شرایط اولیه جدید بنویسیم:

$$\large \left\{ \begin {array} {l} { x _ { m } } \\ { y _ { m} } \end {array} \right\} = \left[ \begin {array} {cc} { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] \left\{\begin {array} {c}{ x _ { 0 } + \varepsilon } \\ { y _ { 0 } + \delta } \end {array} \right\} + \left ( \left[ \begin {array} {cc} { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right] - \left[ \begin {array} {cc} { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { m } \right ) \left ( \left[ \begin {array} {cc} { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right] - \left[ \begin {array} {cc} { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] \right ) ^ { - 1 } \left\{ \begin {array} { l } { 1 } \\ { 2 } \end {array} \right \}$$

با تفریق دو معادله بالا، خواهیم داشت:

$$\large \left \{ \begin {array} { l } { x _ { m } } \\ { y _ { m } } \end {array} \right \} – \left\{ \begin {array} { l } { x _ { n } } \\ { y _ { n } } \end {array} \right \} = \left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { m } \left\{ \begin {array} { l } { x _ {0 } + \varepsilon } \\ { y _ { 0 } + \delta } \end {array} \right\} -\left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { n } \left \{ \begin {array} { l } { x _ { 0 } } \\ { y _ { 0 } } \end {array} \right\} + \\ \large \left < \left ( \left [ \begin {array} {cc} { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right ] – \left [ \begin {array} {cc} { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { m } \right ) \left ( \left[ \begin {array} {cc} { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right] – \left [ \begin {array} {cc} { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right ] \right ) ^ { – 1 } – \\ \large \left ( \left [ \begin {array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right ] – \left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right ] ^ { n } \right ) \left ( \left [ \begin {array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end {array} \right ] – \left [ \begin {array} { l l } { 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right ] \right ) ^ { – 1 } \right > \left \{ \begin {array} { l } { 1 } \\ { 2 } \end {array} \right \}$$

برای بررسی آشوبی بودن این معادله، فرض می‌کنیم $$m = n$$ بوده و عبارت زیر را به دست می‌آوریم:

$$\large \left\{ \begin {array} { l } { x _ { n } } \\ { y _ { n } } \end {array} \right\} - \left \{ \begin {array} { l } { x _ { n } } \\ { y _ { n } } \end {array} \right\} = \left[ \begin {array} { l l }{ 2 } & { 1 } \\ { 1 } & { 2 } \end {array} \right] ^ { n } \left\{ \begin {array} { l } { \varepsilon } \\ { \delta } \end {array} \right\}$$

از آنجایی که مقادیر $$\varepsilon$$ و $$\delta$$ بسیار کوچک هستند، با افزایش مقدار $$n$$، معادله بالا به صفر میل نخواهد کرد. این به دلیل ظاهر شدن ماتریس ضرایب $$\begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ^ n$$ است که در نتیجه نهایی ظاهر می‌شود. در واقع، این عبارت با افزایش $$n$$ به بی‌نهایت میل می‌کند. دلیل این موضوع، مقادیر ویژه ماتریس $$\begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$$ است. اگر یکی یا بیش از یکی از مقادیر ویژه ماتریس بزرگ‌تر از ۱ باشند، آنگاه عبارت مورد نظر به بی‌نهایت میل خواهد کرد. از سوی دیگر، اگر مقادیر ویژه ماتریس کوچک‌تر از ۱ باشند، آنگاه عبارت به صفر می‌گراید. برای ماتریس مشخص $$\begin {bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$$ در این مثال، یکی از مقادیر ویژه ۳ بوده که بزرگ‌تر از ۱ است. بنابراین، در این حالت، با افزایش مقادیر $$n$$ و $$m$$ به بی‌نهایت، نتایج یکسانی برای $$x (n)$$ و $$x ( m )$$ به دست نخواهیم آورد. بنابراین، این معادله رفتار آشوبی دارد.

در حالت کلی، برای دستگاهی از معادلات جبری خطی، بسته به ماتریس ضرایب، ممکن است آشوب رخ دهد یا ندهد. از سوی دیگر، اگر همه مقادیر ویژه ماتریس ضرایب اندازه‌ای کمتر از ۱ داشته باشند، آنگاه دستگاه آشوبی نخواهد بود.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش همزمان سازی سیستم آشوبی به روش کنترل تطبیقی
• مجموعه آموزش‌‌های مهندسی کنترل
• آموزش سیستم های کنترل غیرخطی با رویکرد حل مسأله
• شبکه عصبی در متلب — از صفر تا صد
• تابع مختلط — به زبان ساده
• سیاه چاله چیست؟ — به زبان ساده

^^