مکانیک آماری (Statistical Mechanics) — به زبان ساده

در این مقاله در نظر داریم تا با زبانی ساده به معرفی یکی از زمینههای مهم علم فیزیک، یعنی مکانیک آماری (Statistical Mechanics) بپردازیم. از آنجایی که فیزیک یا مکانیک آماری زمینهای گسترده و وسیع در علم فیزیک است، پرداختن به تمامی جنبههای آن در یک مقاله امکان پذیر نیست. لذا در اینجا سعی بر این داشتهایم تا خلاصهای مفید تنها از تعریف مکانیک آماری ارائه دهیم.
مکانیک آماری که بعضاً به فیزیک آماری نیز شناخته میشود، یکی از بخشهای اساسی فیزیک مدرن به حساب میآید. مکانیک آماری برای مطالعه هر سیستمی که دارای تعداد درجات آزادی زیاد است، استفاده میشود. در واقع رویکرد مکانیک آماری جهت بررسی و مطالعه چنین سیستمهایی، روشهای آماری، تئوری احتمال و قوانین فیزیکی در مقیاس میکروسکوپی است.
فیزیک یا مکانیک آماری، برای توضیح رفتار ترمودینامیک سیستمهای بزرگ نیز قابل استفاده است. در واقع مکانیک آماری بسیار جامعتر از علم ترمودینامیک بوده و آن شاخهای که ترمودینامیک کلاسیکی را تشریح میکند، به ترمودینامیک آماری یا مکانیک آماری تعادلی موسوم است.
میتوان گفت که ترمودینامیک به بررسی، اندازهگیری و مشاهده کمیتهای ماکروسکوپی سیستم (نظیر فشار، دما، ظرفیت گرمایی) میپردازد. حال آنکه مکانیک آماری با نگاهی دقیقتر، با بررسی حالتهای میکروسکوپی سیستم که در نزدیکی یک مقدار متوسط قرار دارند (رویکرد آماری)، کمیتهای ماکروسکوپی را نتیجه گرفته و درباره چرایی و چگونگی تغییر آنها از دیدگاه میکروسکوپی صحبت میکند.
جدا از حالتهای تعادلی، مکانیک آماری برای تشریح سیستمهای غیرتعادلی نیز قابل استفاده است. این شاخه که به مکانیک آماری غیرتعادلی موسوم است، با مدلسازی سرعت فرآیندهای برگشتناپذیر ناشی از عدم تعادل سیستم، به بررسی و تشریح سیستمهای غیرتعادلی میپردازد. به طور مثال میتوان به بررسی فرآیندهای (واکنشهای) شیمیایی یا جریان ذرات یا گرما اشاره کرد.
یکی از مباحثی که در مکانیک آماری غیرتعادلی مطرح میشود، قضیه fluctuation–dissipation است. قضیه مذکور دانشی پایهای است که از مکانیک آماری غیرتعادلی برای مطالعه سادهترین وضعیتهای غیرتعادلی جریان ذرات در سیستمها استفاده میکند.
اصول مکانیک آماری و آنسامبل
معمولاً در فیزیک پدیدههای مختلف توسط دو نوع مکانیک (رویکرد) کلاسیک و کوانتومی مورد بررسی قرار میگیرند. هر دو نوع مکانیک، قوانین و رویکردهای ریاضی متفاوتی را برای بررسی سیستم، پیش میگیرند.
حالت یک سیستم مکانیکی در یک زمان مشخص، به صورت ریاضی در مکانیک کلاسیک توسط نقطه فاز و در مکانیک کوانتومی توسط بردارهای حالت نشان داده میشود. همچنین معادله حرکت یا به طور جامعتر معادلهای که وضعیت سیستم را مشخص میکند، در مکانیک کلاسیک توسط معادلات هامیلتونی و در مکانیک کوانتومی با معادله شرودینگر وابسته به زمان مشخص میشود.
با توجه به مطلب فوق، حالت سیستم در زمانهای دیگر (آینده و گذشته) قابل محاسبه است. اما با این حال، میتوان گفت که بین این قوانین و تجربیات روزمره زندگی ما یک خلأ وجود دارد. البته این شکاف خللی در عملکرد قوانین یاد شده ایجاد نمیکند. به طور مثال در حین انجام یک واکنش شیمیایی لزومی ندارد تا در مقیاس میکروسکوپی از مقادیر دقیق سرعت تک تک مولکولها و موقعیت مکانی آنها اطلاع داشته باشیم. به هر حال جهت تکمیل قوانین فیزیکی، مکانیک آماری با رویکردی آماری و در نظر گرفتن تک تک اجزای سیستم، سعی در پر کردن این شکاف دارد.
دو مکانیک کلاسیک و کوانتومی تنها رفتار یک حالت مشخص از سیستم را در نظر گرفته و آن را تحلیل میکنند. اما مکانیک آماری، یک گروه بزرگ آماری موسوم به «آنسامبل» (ensemble) را معرفی کرده و با رویکردیهای آماری تمامی حالتهای مختلف سیستم را بررسی میکند.
به طور ساده انسامبل را میتوان یک توزیع احتمال از تمامی حالات مختلف سیستم در نظر گرفت. البته خود مکانیک آماری را نیز میتوان به دو مجموعه کلاسیک و کوانتومی تقسیمبندی کرد. مکانیک آماری کلاسیکی، انسامبل یک توزیع احتمال در نقاط فاز (برخلاف یک نقطه فاز در مکانیک کلاسیک معمولی) است که به صورت یک توزیع فضای فاز در مختصات متعارف (canonical) نمایش داده میشود. در مکانیک آماری کوانتومی نیز، انسامبل توزیع احتمالی در حالتهای خالص (pure states) است که به وسیله ماتریسی به نام ماتریس چگالی (density matrix) نمایش داده میشود.

تعریف آنسامبل
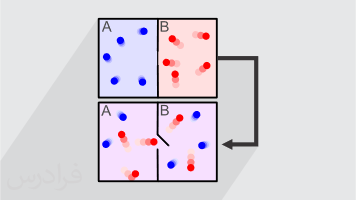
آنسامبل آماری یا هنگرد، به مجموعهای که شامل تعداد بسیار زیادی از یک سیستم (سامانه) فیزیکی باشد، گفته میشود. این سیستمها در یک آنسامبل از نظر ماهیت، مشابه یکدیگر بوده، اما هر کدام در وضعیت یا حالتهای خاصی قرار دارند. با این اوصاف، میتوان یک آنسامبل را توزیع احتمالی در نظر گرفت که وضعیتهای ممکن سیستمهای فیزیکی را برای یک سیستم بزرگتر نشان میدهد. به طور مثال مولکولهای گاز را میتوان جداگانه یک سیستم در نظر گرفت که در یک سیستم بزرگتر مثل کپسول هستند که سرعت حرکتشان از تابع توزیع ماکسولی تبعیت میکند.
آنسامبل ترمودینامیکی نیز نوع خاصی از آنسامبل آماری است که در حالت تعادل بوده و جهت بررسی ویژگیهای یک سیستم ترمودینامیکی به کار میرود.
از آنجایی که روشهای مختلفی جهت تفسیر آماری و احتمالاتی یک سیستم وجود دارد، انسامبل نیز میتواند به طرق مختلفی تفسیر شود.
ترمودینامیک آماری
هدف اصلی ترمودینامیک آماری که به مکانیک آماری تعادلی نیز موسوم است، نتیجه گرفتن ترمودینامیک کلاسیک از خواص میکروسکوپی ذرات تشکیل دهنده سیستم است. به عبارت دیگر، ترمودینامیک آماری، ارتباط بین خصوصیات ماکروسکوپی و میکروسکوپی ماده را مشخص میکند. دقت شود که ترمودینامیک آماری تنها حالت خاص یا قسمت کوچکی از علم بزرگتر مکانیک آماری است که برای سیستمهای پویایی که مدام در حال تغییر هستند، استفاده میشود.
نکته دیگری که در اینجا باید به آن دقت کنید، مفهوم تعادل آماری است. در اینجا واژه تعادل به این معنی نیست که ذرات سیستم از حرکت ایستاده و متوقف شدهاند (منظور تعادل مکانیکی نیست)، بلکه منظور این است که انسامبل در حال تحول سریع نیست. در مقاله «فرآیندهای ترمودینامیکی -- به زبان ساده» دیدیم که اگر فرآیندها را شبهاستاتیک فرض کنیم، میتوانیم برای هر لحظه از سیستم معادله حالت را بنویسیم.

مکانیک آماری غیر تعادلی
بسیاری از پدیدههای فیزیکی را میتوان فرآیندهای شبهترمودینامیکی که غیرتعادلی هستند در نظر گرفت، به عنوان مثال:
- انتقال حرارت توسط حرکتهای داخلی ذرات در یک ماده به دلیل عدم تعادل دمایی
- جریان الکتریکی که با حرکت بارها (الکترونهای آزاد) در یک رسانا به دلیل عدم تعادل ولتاژ (وجود اختلاف پتانسیل) ناشی میشود.
- واکنشهای شیمیایی خودبهخودی ناشی از تغییر انرژی و فرآیندهای برگشتناپذیر
- اصطکاک، اتلاف، ناهمدوسی کوانتومی
- سیستمهایی که توسط نیروهایی خارجی پمپ میشوند، نظیر پمپهای نوری در لیزرهای فیبری
تمامی فرآیندهای فوق، به مرور زمان با نرخهای متفاوتی میتوانند رخ دهند که برای مهندسان در کاربردهای مختلف حائز اهمیت است. مکانیک آماری غیرتعادلی به مطالعه این دست از فرآیندهای غیرتعادلی در سطح میکروسکوپی میپردازد. دقت شود که مکانیک آماری تعادلی (ترمودینامیک آماری) تنها برای محاسبه و پیشبینی سیستمهای فوق که به تعادل رسیدهاند، استفاده میشود.
میتوان گفت که مکانیک آماری غیرتعادلی برای بررسی و تحلیل سیستمهای پیچیده و غیرتعادلی از ریاضیات دقیق و البته پیچیدهای استفاده میکند. به طور مثال آنسامبل یک سیستم ایزوله، توسط «معادله لیوولی» (Liouville's equation) یا همارز کوانتومی آن، معادله «وون نویمان» (von Neumann) نتیجه و تحلیل میشود. این دو معادله، نتیجه اعمال معادلات مکانیکی حرکت به هر حالت سیستم در آنسامبل هستند. بدیهی است که تعداد معادلات برای چنین سیستمهایی میتواند بسیار زیاد باشد.
با این اوصاف تحلیل چنین آنسامبلهایی بسیار دشوار است. البته میتوان حفظ شدن آنتروپی گیبس را برای آنسامبل، یک مزیت از این معادلات تکاملی آنسامبل دانست. در واقع این معادلات برگشتپذیراند و اطلاعات سیستم در آن حالت را از بین نمیبرند.
دوره ویدئویی آموزش مکانیک آماری
در صورتی که علاقهمند به یادگیری جزئی و تخصصیتر در خصوص مطالب ذکر شده هستید، دوره آموزش ویدئویی زیر به شما پیشنهاد میشود:
- آموزش مبانی مکانیک آماری پیشرفته ۱ (لینک آموزش)
دوره فوق، مطابق با واحد دانشگاهی مکانیک آماری در مقطع کارشناسی ارشد رشته فیزیک (تمامی گرایشها) بوده و به دانشجویان سال آخر دوره کارشناسی فیزیک و دانشجویان مقاطع تحصیلات تکمیلی رشتههای فیزیک، شیمی، مهندسی مواد و مهندسی مکانیک پیشنهاد میشود.
رئوس مطالب تدوین شده دوره مذکور، طی 8 فصل در 12 ساعت به شرح ذیل است:
- فصل اول به طور کامل به مبانی علم ترمودینامیک میپردازد.
- فصل دوم به نظریه آنسامبل و تعاریف مربوطه اختصاص دارد.
- فصل سوم و چهارم نیز به طور کامل به تشریح آنسامبل بندادی (کانونیک) و کانونیک بزرگ و همچنین مکانیک آماری تعادلی (ترمودینامیک تعادلی) اختصاص دارد.
- فصل پنجم به معرفی و تشریح مکانیک آماری کوانتومی میپردازد.
- فصل ششم به بررسی تئوری گازهای کامل با رویکرد مکانیک آماری کوانتومی (آنسامبلهای کوانتومی) میپردازد.
- فصل هفتم و هشتم نیز به ترتیب و طور کامل به بررسی سیستمهای بوزونی و فرمیونی میپردازند.
در این آموزش، سعی بر این است که مباحث مختلف در قالب مثالهایی کاربردی و با نگرش حل مسئله بیان شوند. از آنجایی که تمامی مطالب، تا جای ممکن در طی دوره پوشش داده میشوند، تنها آشنایی با ترمودینامیک کلاسیک و مباحث مقدماتی مکانیک کوانتومی به عنوان پیشنیازهای دوره فوق کافی هستند.
^^













سلام و وقت بخیر
متشکرم از زحمات شما ولی مطلب به خوبی تببین نشده یعنی غیر فیزیکی ها چیزی متوجه نمی شوند.
درود خسته نباشید دوست جوان عزیز احساس میکنم مطالب شما در مورد مکانیک اماری کپی پراکنده است . دوست عزیز به نظر من وقتی میخواهید مفاهیم را بزبان ساده بیان کنید باید به مطلب اشراف کامل داشته و بتوانید مطالب پیچیده علمی را ساده سازس کنید که تسلط بالا بر مطلب و ابتکارو طرح ممثالهای جالب و ملموس میخواهد مطالبی که شما بظاهر ساده نوشتید خواننده را گیج فراری میکند یکبار دیگر مطلب خودتان را بخوانید ایا خودتان سر در می اورید چی نوشتید
شیر بی یال و دم و اشکم
بیشتر سعی کنید موفق باشید
سلام به گروه خوب بچه های فرادرس
ممنون و سپاس ویژه و خاص و البته دست مریزاد به تمامی نویسندگان مقاله به ویژه در دو زمینه ریاضی و فیزیک (که زمینه خودم است).
جدا از تمامی پیشنهادات و انتقادات، چون مطالب سایت شما را هم نگاه میکنم بسیار ممنون خواهم شد اگر منابعی که این مطالب را از آن می گیرد ذکر کنید. در بیان مطالب علمی، این کار رکن اساسی محسوب می شود و بدون ذکر منابع هیچ اعتمادی نمی شود و گاها” هیچ ارزشی برای مخاطب ندارد. قطعا” نویسندگان مقالات شما در این دو زمینه که تحصیلات ارزنده ای دارند این را بهتر از من میدانند.
سلام، وقت شما بخیر؛
منابع کلیه مطالب مجله فرادرس در انتهای آنها و پس از معرفی آموزشها و مطالب مرتبط درج شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.